全排列[中等]
优质博文:IT-BLOG-CN
一、题目
给定一个不含重复数字的数组nums,返回其所有可能的全排列。你可以按任意顺序返回答案。
示例 1:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
示例 2:
输入:nums = [0,1]
输出:[[0,1],[1,0]]
示例 3:
输入:nums = [1]
输出:[[1]]
提示:
1 <= nums.length <= 6
-10 <= nums[i] <= 10
nums 中的所有整数 互不相同
二、代码
全排列的长度就是数据长度的阶层,排列和组合的区别:排列中[1,2]和[2,1]是不同的,但在组合中[1,2]和[2,1]是相同的。
我们已简单的[1,2,3]为一组,看下排列的搜索树:
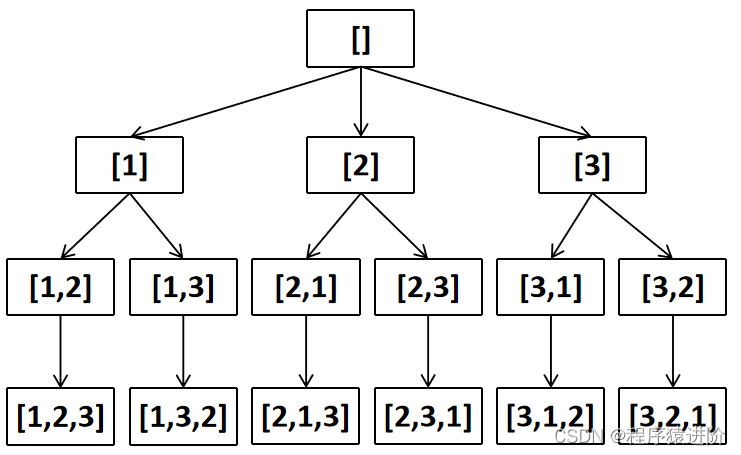
解题思路:
【1】使用数组path记录路径上的数(已选数字)
【2】集合s记录剩余未选的数
回溯三问:
【1】当前操作?从s中枚举path[i]要填入的数字x;
【2】子问题?构造排列 >= i 的部分,剩余未选数字集合为s;
【3】下一个子问题?构造排列 >= i + 1 部分,剩余未选数字结合为s-{x};
class Solution {// 入参private int[] nums;// 返回值private final List<List<Integer>> resList = new ArrayList<>();// 返回值中包的Listprivate List<Integer> path;// 过滤 j 使用private boolean[] onPath;public List<List<Integer>> permute(int[] nums) {this.nums = nums;path = Arrays.asList(new Integer[nums.length]);onPath = new boolean[nums.length];dfs(0);return resList;}// 回溯方法private void dfs(int i) {// 回溯方法的退出条件if (i == nums.length) {// 这里需要copy path, 不能直接赋值,因为path一直变化resList.add(new ArrayList(path));System.out.println("resList : " + resList.toString());return;}// 每个i进来,组装一次结果for (int j = 0; j < nums.length; j++) {// 过滤j,原因在循环中有说明if (!onPath[j]) {// 当 i 递增时,j也在递增path.set(i, nums[j]);System.out.println(path.toString());// 回溯 (此时,i= 1调用的时候,j还是0,所以需要过滤掉j=0,因此添加 onPath 的Boolean数组)onPath[j] = true;dfs(i+1);// 当i遍历完成之后,需要恢复现场onPath[j] = false;}}}
}
看下输出的流程:
[1, null, null]
[1, 2, null]
[1, 2, 3]
resList : [[1, 2, 3]]
[1, 3, 3]
[1, 3, 2]
resList : [[1, 2, 3], [1, 3, 2]]
[2, 3, 2]
[2, 1, 2]
[2, 1, 3]
resList : [[1, 2, 3], [1, 3, 2], [2, 1, 3]]
[2, 3, 3]
[2, 3, 1]
resList : [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1]]
[3, 3, 1]
[3, 1, 1]
[3, 1, 2]
resList : [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2]]
[3, 2, 2]
[3, 2, 1]
resList : [[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
附视频讲解
时间复杂度: O(n⋅n!),其中n为nums的长度。搜索树中的节点个数低于3⋅n!。实际上,精确值为⌊e⋅n!⌋,其中e=2.718⋯为自然常数。每个非叶节点要花费O(n)的时间遍历onPath数组,每个叶结点也要花费O(n)的时间复制path数组,因此时间复杂度为O(n⋅n!)。
空间复杂度: O(n)返回值的空间不计入。
相关文章:

全排列[中等]
优质博文:IT-BLOG-CN 一、题目 给定一个不含重复数字的数组nums,返回其所有可能的全排列。你可以按任意顺序返回答案。 示例 1: 输入:nums [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]] 示例…...
mybatise-plus的id过长问题
一、问题情景 笔者在做mp插入数据库(id已设置为自增)操作时,发现新增数据的id过长,结果导致前端JS拿到的数据出现了精度丢失问题,原因是后端id的类型是Long。在网上查了一下,只要在该属性上加上如下注解就可以 TableId(value &q…...
图示矩阵分解
特征值与特征向量 设 A A A 是 n 阶矩阵,如果存在数 λ \lambda λ 和 n 维非零列向量 x x x,满足关系式: A x λ x ( 1 ) Ax \lambda x\quad\quad(1) Axλx(1) 则数 λ \lambda λ 称为矩阵 A A A 的特征值,非零向量 x…...
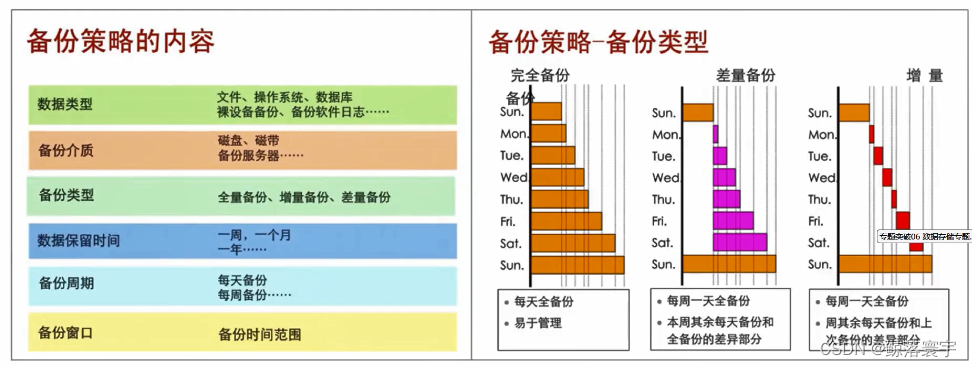
六、互联网技术——数据存储
文章目录 一、存储系统层次结构二、按照重要性分类三、磁盘阵列RAID三、RAID基础四、磁盘阵列分级五、数据备份与恢复六、容灾与灾难恢复 一、存储系统层次结构 常见的三层存储体系结构如下图所示,分为高速缓冲存储器、主存储器和外存储器。 二、按照重要性分类 …...

六、vpp 流表+负载均衡
草稿!!! vpp node其实就是三个部分 1、plugin init 2、set command 3、function 实现功能,比如这里的流表 今天我们再用VPP实现一个流表的功能 一、流表 1.1流表----plugin init VLIB_REGISTER_NODE 注册流表节点 // 注册流…...
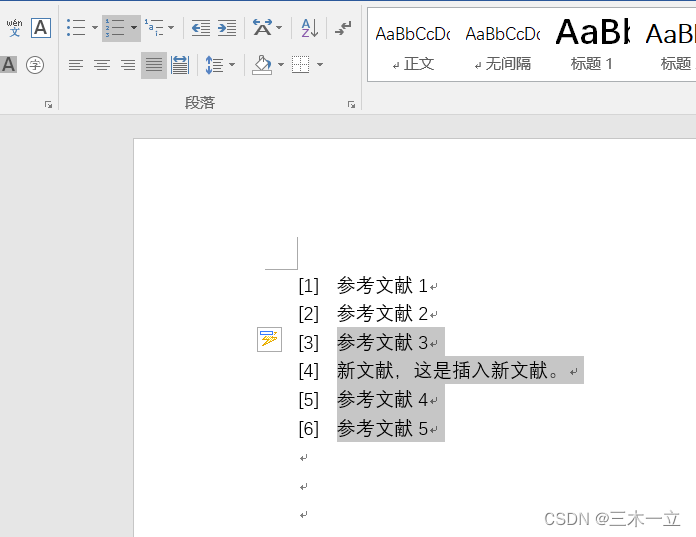
word已排序好的参考文献,插入新的参考文献,序号更新
原排序好的文献序号。 现在在3号后面插入一个新文献。4,5号应该成为5,6 这时在3号后面,回车,就会自动的增长。如下图: 但是如果手滑,把[4]删除了如何排序?? 如下图: …...
二叉树的顺序存储——堆——初识堆排序
前面我们学过可以把完全二叉树存入到顺序表中,然后利用完全二叉树的情缘关系,就可以通过数组下标来联系。 但是并不是把二叉树存入到数组中就是堆了,要看原原来的二叉树是否满足:所有的父都小于等于子,或者所有的父都…...

CYEZ 模拟赛 9
A a ⊥ b ⇒ a − b ⊥ a b (1) a \perp b \Rightarrow a-b \perp ab \tag {1} a⊥b⇒a−b⊥ab(1) 证明: gcd ( a , b ) gcd ( b , a − b ) \gcd(a,b) \gcd(b, a-b) gcd(a,b)gcd(b,a−b),故 a − b ⊥ b a - b \perp b a−b⊥b,同…...
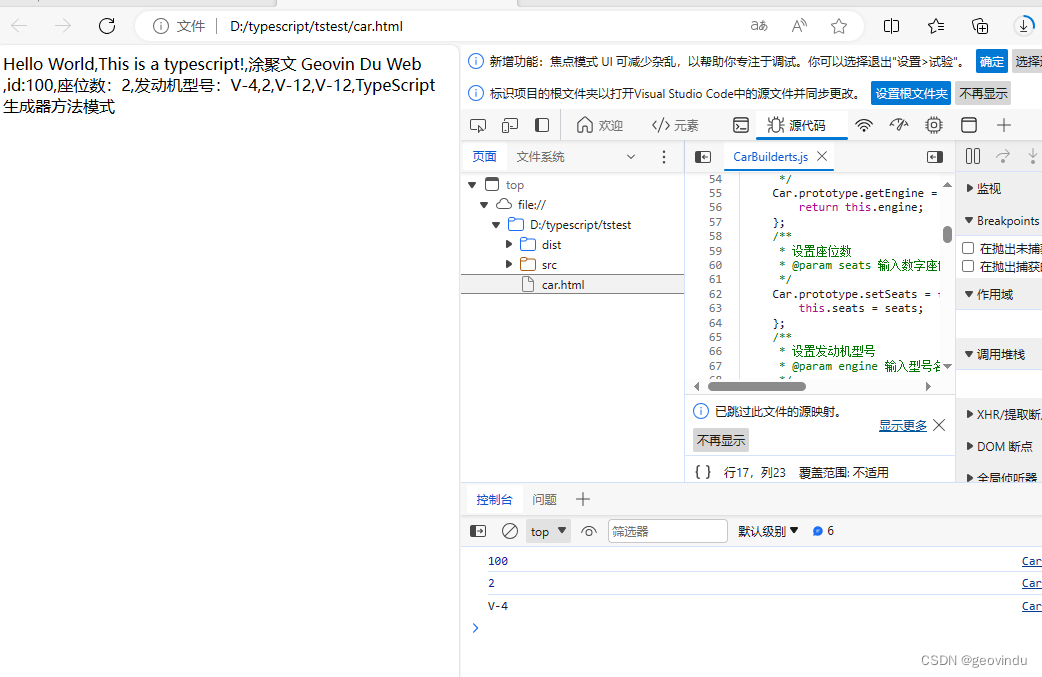
typescript: Builder Pattern
/*** file: CarBuilderts.ts* TypeScript 实体类 Model* Builder Pattern* 生成器是一种创建型设计模式, 使你能够分步骤创建复杂对象。* https://stackoverflow.com/questions/12827266/get-and-set-in-typescript* https://github.com/Microsoft/TypeScript/wiki/…...
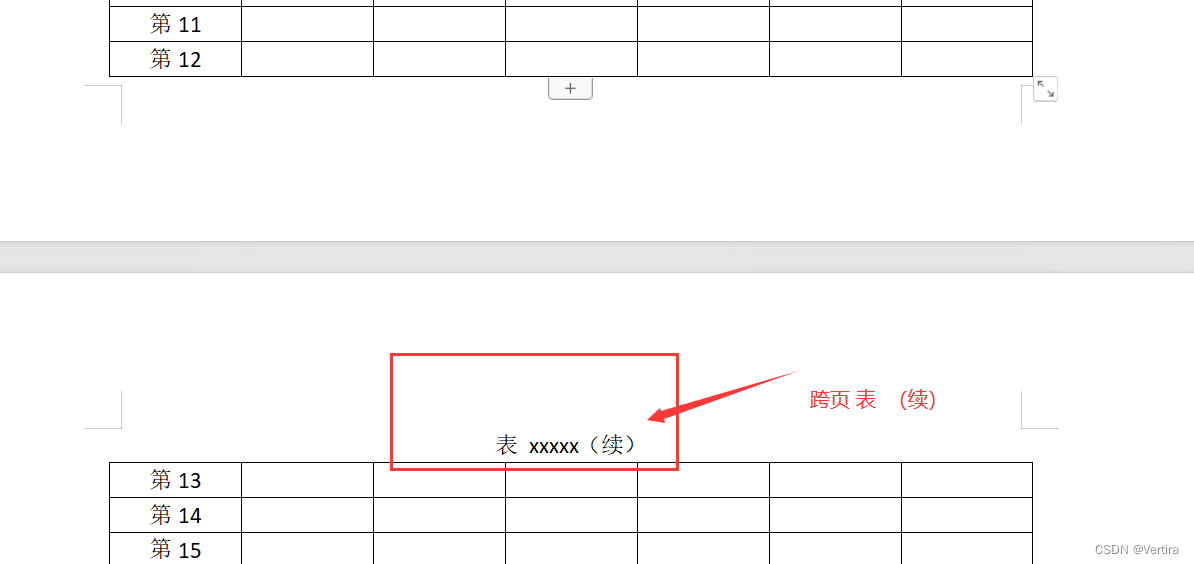
WPS/word 表格跨行如何续表、和表的名称
1:具体操作: 将光标定位在跨页部分的第一行任意位置,按下快捷键ctrlshiftenter,就可以在跨页的表格上方插入空行(在空行可以写,表1-3 xxxx(续)) 在空行中输入…...
Python的NumPy库(一)基础用法
NumPy库并不是Python的标准库,但其在机器学习、大数据等很多领域有非常广泛的应用,NumPy本身就有比较多的内容,全部的学习可能涉及许多的内容,但我们在这里仅学习常见的使用,这些内容对于我们日常使用NumPy是足够的。 …...
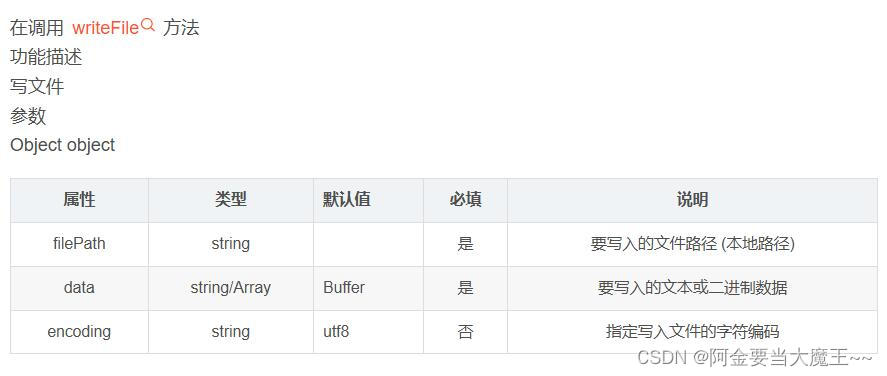
uniapp app 导出excel 表格
直接复制运行 <template><view><button click"tableToExcel">导出一个表来看</button><view>{{ successTip }}</view></view> </template><script>export default {data() {return {successTip: }},metho…...
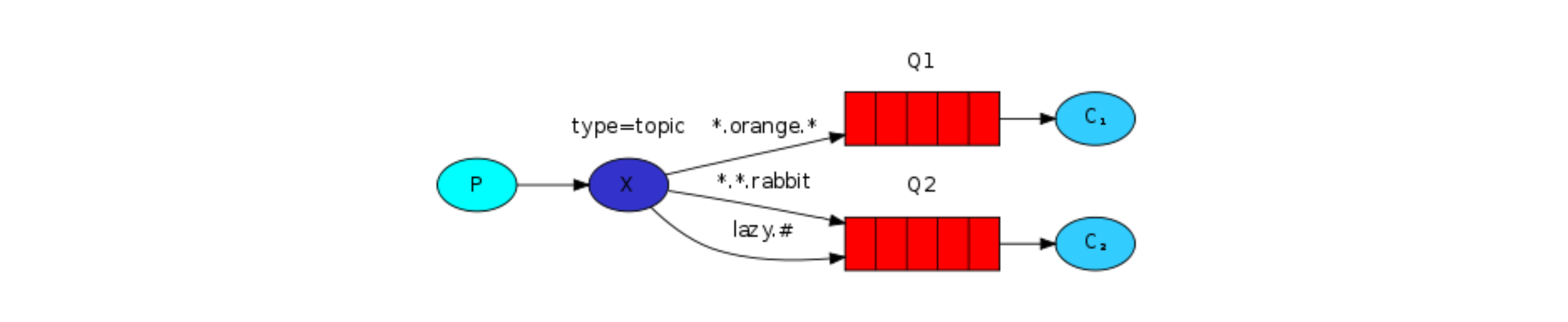
【RabbitMQ】常用消息模型详解
文章目录 AMQP协议的回顾RabbitMQ支持的消息模型第一种模型(直连)开发生产者开发消费者生产者、消费者开发优化API参数细节 第二种模型(work quene)开发生产者开发消费者消息自动确认机制 第三种模型(fanout)开发生产者开发消费者 第四种模型(Routing)开发生产者开发消费者 第五…...

图像拼接后丢失数据,转tiff报错rasterfile failed: an unknown
图像拼接后丢失数据 不仅是数据丢失了,还有个未知原因报错 部分数据存在值不存在的情况 原因 处理遥感数据很容易,磁盘爆满了 解决方案 清理一些无用数据,准备买个2T的外接硬盘用着了。 然后重新做处理...

Nginx之日志模块解读
目录 基本介绍 配置指令 access_log(访问日志) error_log( 错误日志) 基本介绍 Nginx日志主要分为两种:access_log(访问日志)和error_log(错误日志)。Nginx日志主要记录以下信息: 记录Nginx服务启动…...
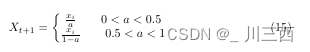
latex方程组编写,一种可以保证方程编号自适应的方法
问题描述: 在利用latex编写方程组时,可以有很多种方法,但不总是编辑好的公式能够显示出编号,故提出一种有效的方程组编写方法 方法: \begin{equation}X_{ t1}\left \{ \begin{matrix}\frac{x_{i}}{a} \quad\quad 0&l…...
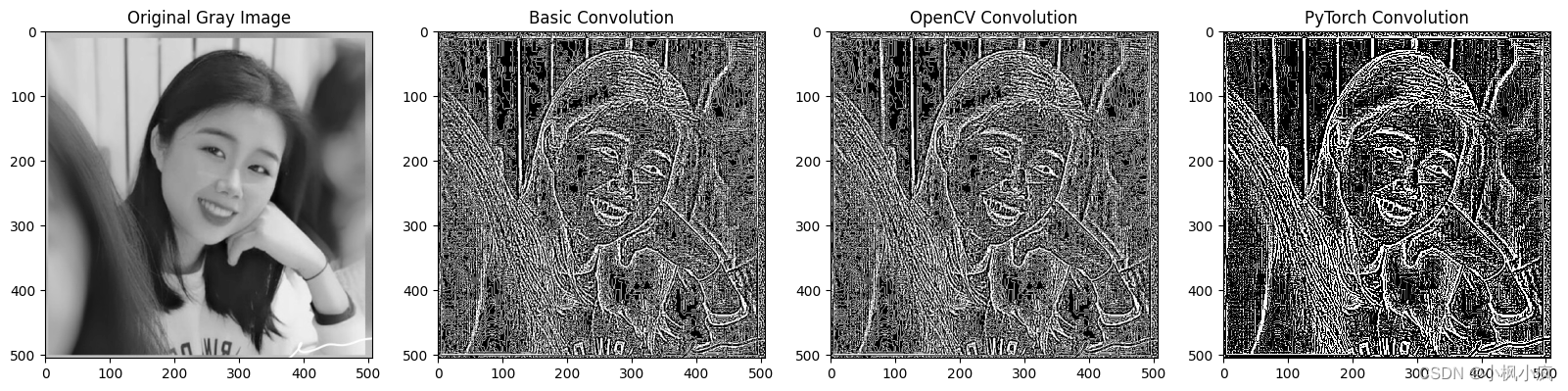
深度学习基础 2D卷积(1)
什么是2D卷积 2D参数量怎么计算 以pytorch为例子,2D卷积在设置的时候具有以下参数,具有输入通道的多少(这个决定了卷积核的通道数量),滤波器数量,这个是有多少个滤波器,越多提取的特征就越有用…...

OpenCV DNN C++ 使用 YOLO 模型推理
OpenCV DNN C 使用 YOLO 模型推理 引言 YOLO(You Only Look Once)是一种流行的目标检测算法,因其速度快和准确度高而被广泛应用。OpenCV 的 DNN(Deep Neural Networks)模块为我们提供了一个简单易用的 API࿰…...
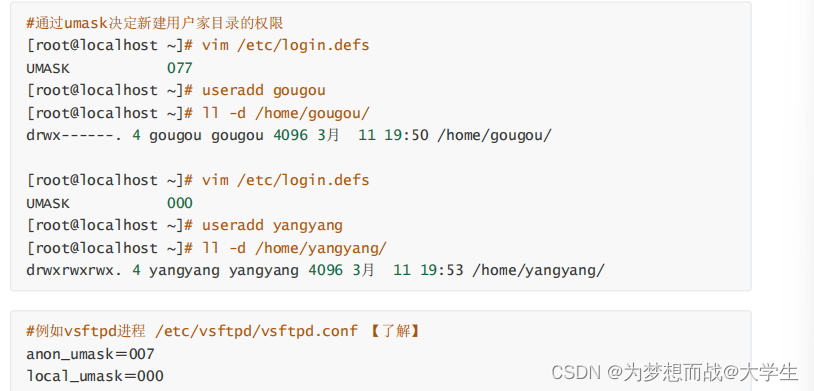
第八章 Linux文件系统权限
目录 8.1 文件的一般权限 1.修改文件或目录的权限---chmod命令 2.对于文件和目录,r,w,x有不同的作用: 3.修改文件或目录的所属主和组---chown,chgrp 8.2 文件和目录的特殊权限 三种通过字符描述文件权限 8.3 ACL 权限 1.A…...
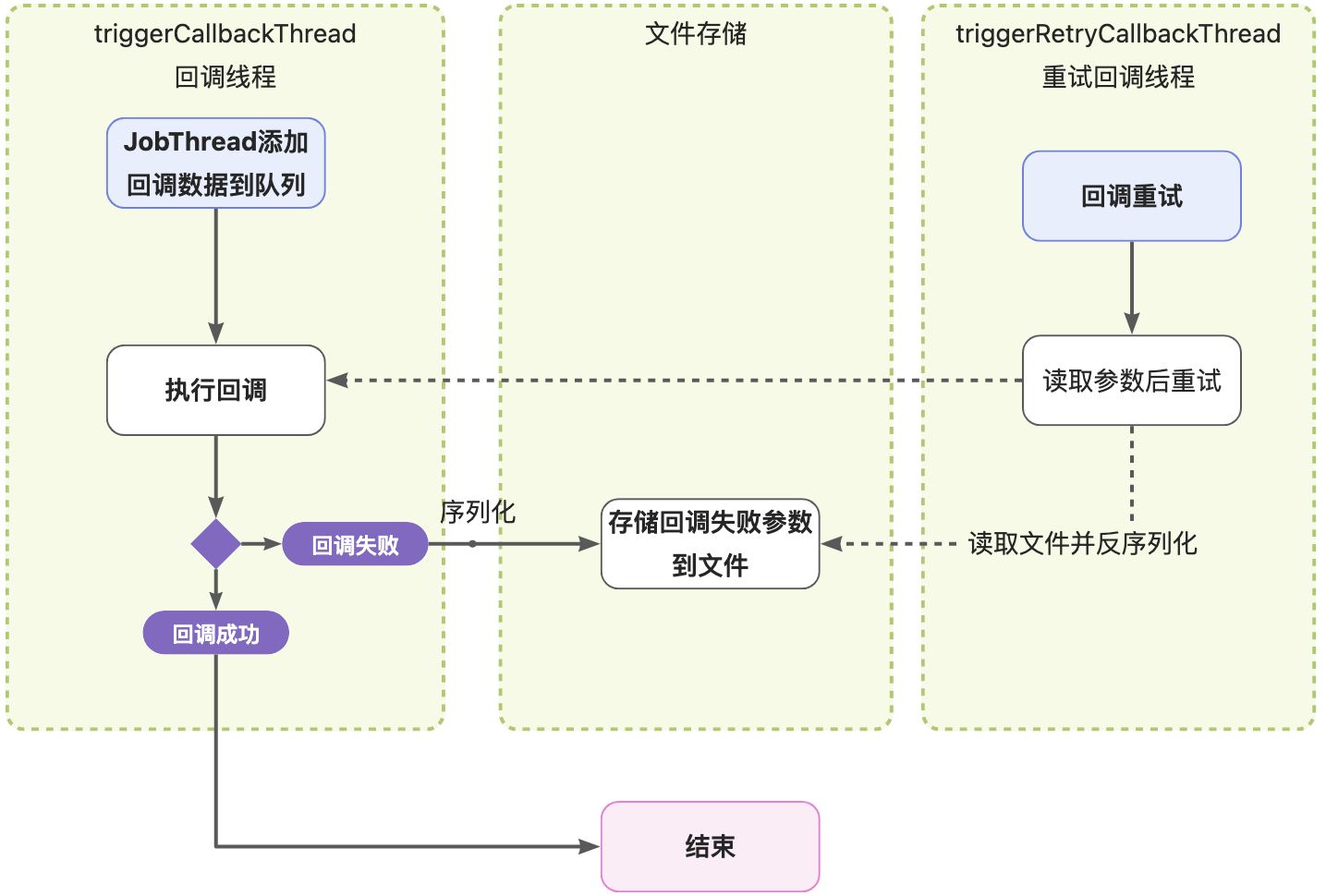
XXL-JOB源码梳理——一文理清XXL-JOB实现方案
分布式定时任务调度系统 流程分析 一个分布式定时任务,需要具备有以下几点功能: 核心功能:定时调度、任务管理、可观测日志高可用:集群、分片、失败处理高性能:分布式锁扩展功能:可视化运维、多语言、任…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
