【树】树的直径和重心
目录
一.树的直径
(1)定义
(2)思路
(3)例题
(4)std(第一小问)
二.树的重心
(1)介绍
(2)求重心
(3)例题
(4)AC
一.树的直径
(1)定义
树的直径是指树中最长的一条路径的长度,这条路径连接树中的两个节点,使得它们之间的距离最远。
(2)思路
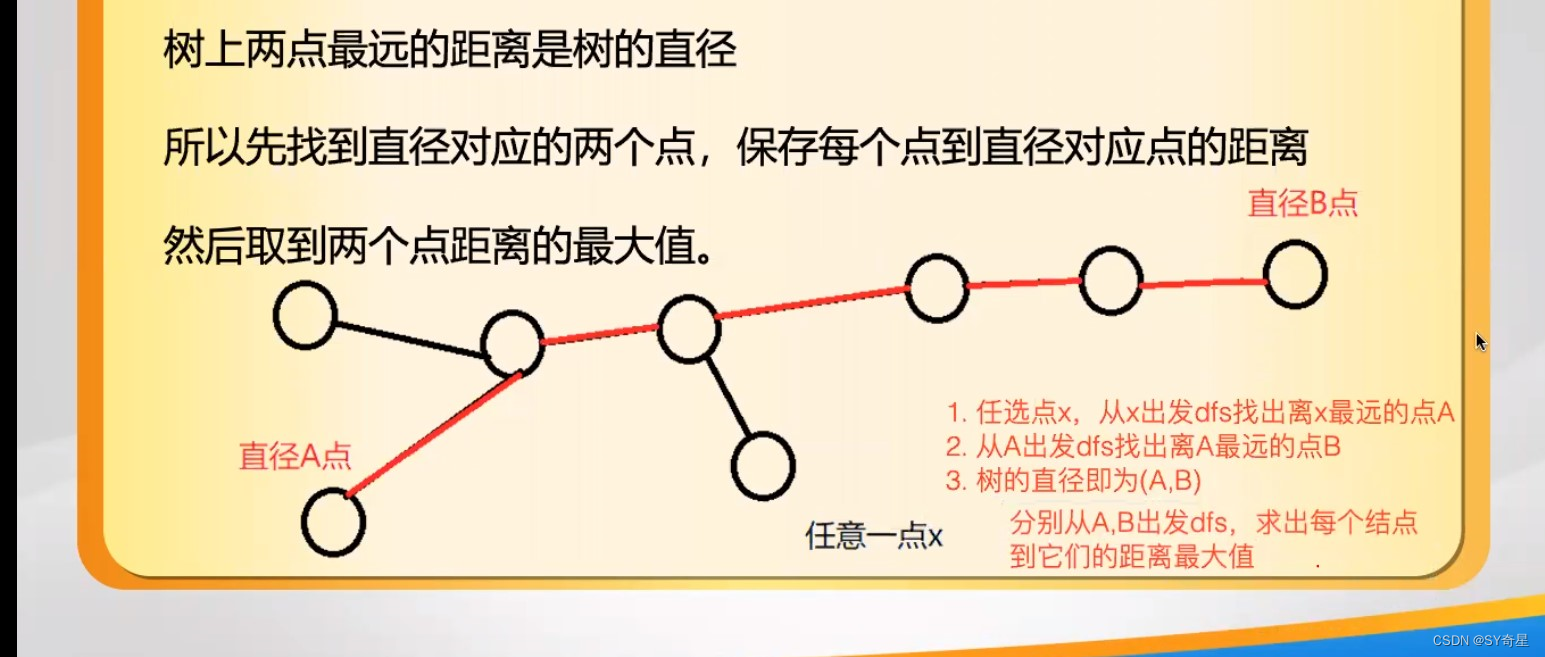
(3)例题
P3304 [SDOI2013] 直径 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
(4)std(第一小问)
#include<bits/stdc++.h>
using namespace std;
const int maxn=2e5+5;
int n;
struct Edge{int u,v,w,next;
}edge[maxn<<1];
int head[maxn],cnt;
void add(int u,int v,int w){edge[++cnt]=(Edge){u,v,w,head[u]}; head[u]=cnt;
}
int root,lon;
void dfs(int u,int fa,int p){if(p>lon){root=u;lon=p;}for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(v==fa) continue;dfs(v,u,p+edge[i].w);}
}
int main(){scanf("%d",&n);for(int i=1,u,v,w;i<n;i++){scanf("%d%d%d",&u,&v,&w);add(u,v,w); add(v,u,w);}dfs(1,0,0);lon=0;dfs(root,0,0);printf("%d",lon);return 0;
}
二.树的重心
(1)介绍
树的重心是指树中的一个节点,通过删除该节点后,将树分成多个子树,使得每个子树的节点数都不超过整棵树节点数的一半。换句话说,树的重心是树的一种结构特征,它能够将树尽可能平衡地分割成多个相对均匀的部分。
说人话就是重心在树所有节点中,它的最大子树的节点最小
寻找树的重心通常可以通过以下步骤来实现:
- 选择任意一个节点作为树的根节点。
- 对树进行深度优先搜索(DFS)或广度优先搜索(BFS),计算每个节点的子树大小(包括自身节点)。
- 对于每个节点,计算删除该节点后,各个子树的大小(即除去该节点后,以其邻居节点为根的子树大小)。
- 找到一个节点,使得删除该节点后,各个子树的大小都不超过整棵树节点数的一半。这个节点就是树的重心。
(2)求重心
#include<bits/stdc++.h>
#define maxn 10005
using namespace std;
int n;
int size[maxn],f[maxn]; //子树总大小 && 最大子树
struct Edge{int u,v,next;
}edge[maxn<<1];
int head[maxn],cnt;
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]}; head[u]=cnt;
}
int root,MAX=0x7fffffff;
void dfs(int u,int fa){size[u]=1;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(v!=fa){dfs(v,u);size[u]+=size[v];f[u]=max(f[u],size[v]);}}f[u]=max(f[u],n-size[u]);if(f[u]<MAX ||f[u]<=MAX && u<root){MAX=f[u];root=u;}
}int main(){scanf("%d",&n);int x,y;for(int i=1;i<n;i++){scanf("%d%d",&x,&y);add(x,y); add(y,x);}dfs(1,0);printf("%d",root);return 0;
}(3)例题
P1395 会议 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
(4)AC
#include<bits/stdc++.h>
#define maxn 50005
using namespace std;
int n;
int size[maxn],f[maxn]; //子树总大小 && 最大子树
struct Edge{int u,v,w,next;
}edge[maxn<<1];
int head[maxn],cnt;
void add(int u,int v,int w){edge[++cnt]=(Edge){u,v,w,head[u]}; head[u]=cnt;
}
int root,MAX=0x7fffffff;
void dfs(int u,int fa){size[u]=1;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(v!=fa){dfs(v,u);size[u]+=size[v];f[u]=max(f[u],size[v]);}}f[u]=max(f[u],n-size[u]);if(f[u]<MAX ||f[u]<=MAX && u<root){MAX=f[u];root=u;}
}
struct node{int u,w;bool operator < (const node &x) const{return x.w<w;}
};
int dis[maxn],vis[maxn];
void Djkstra(){for(int i=1;i<=n;i++) dis[i]=0x7fffffff;dis[root]=0;priority_queue<node> q;q.push((node){root,0});while(!q.empty()){node temp=q.top(); q.pop();int u=temp.u;if(vis[u]) continue;vis[u]=1;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v,w=edge[i].w;if(dis[u]+w<dis[v]){dis[v]=dis[u]+w;q.push((node){v,dis[v]});}}}
}
int main(){scanf("%d",&n);int x,y;for(int i=1;i<n;i++){scanf("%d%d",&x,&y);add(x,y,1); add(y,x,1);}dfs(1,0);printf("%d ",root);Djkstra();long long ans=0;for(int i=1;i<=n;i++) ans+=dis[i];printf("%lld",ans);return 0;
}
相关文章:

【树】树的直径和重心
目录 一.树的直径 (1)定义 (2)思路 (3)例题 (4)std(第一小问) 二.树的重心 (1)介绍 (2)求重心 (3)例…...

《Attention Is All You Need》论文笔记
下面是对《Attention Is All You Need》这篇论文的浅读。 参考文献: 李沐论文带读 HarvardNLP 《哈工大基于预训练模型的方法》 下面是对这篇论文的初步概览: 对Seq2Seq模型、Transformer的概括: 下面是蒟蒻在阅读完这篇论文后做的一…...

C++笔记之不同buffer数量下的生产者-消费者机制
C笔记之不同buffer数量下的生产者-消费者机制 文章目录 C笔记之不同buffer数量下的生产者-消费者机制0.在不同的缓冲区数量下,生产者-消费者机制的实现方式和行为的区别1.最简单的生产者-消费者实现:抄自 https://mp.weixin.qq.com/s/G1lHNcbYU1lUlfugXn…...

编码文字使用整数xyz 三个坐标 并使用
导航 说明原始描述AI理解的实现代码说明 原始描述 而后期的,相同的s,前缀差距 和 自身权重 要对应的上,或者说 假设每个序列都是三维空间上的点集合,使用最小的空间表达这些信息,整个数据集才是重点。这些点的集合可以 是空间直线或者是曲线 整体的思路是 一个集合能在任…...
创建vue3工程
一、新建工程目录E:\vue\projectCode\npm-demo用Visual Studio Code 打开目录 二、点击新建文件夹按钮,新建vue3-01-core文件夹 三、右键vue3-01-core文件夹点击在集成终端中打开 四、初始化项目,输入npm init 一直敲回车直到创建成功如下图 npm init 五…...

Flutter笔记 - 用于描述Align的Alignment、AlignmentDirectional、AlignmentTween类
Flutter笔记 用于描述Align的Alignment、AlignmentDirectional、AlignmentTween类 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_…...

门面模式简介
门面模式简介 门面模式(Facade Pattern)是一种结构性设计模式,它提供了一个简化复杂系统的接口,允许客户端通过一个统一的接口与系统交互,而不需要了解系统内部的复杂性。这个模式的目标是降低客户端与系统之间的耦合…...

2023年7月工作经历二
invoke的翻译 C#的这个关键字很熟,但不知道如何翻译比较好。和网友沟通,并查阅多篇博文,觉得“同步调用(invoke)和异步调用(beginvoke)”比较好。 VS2022很爽 C#的类名,会提示命名空间。C调试的时候&…...
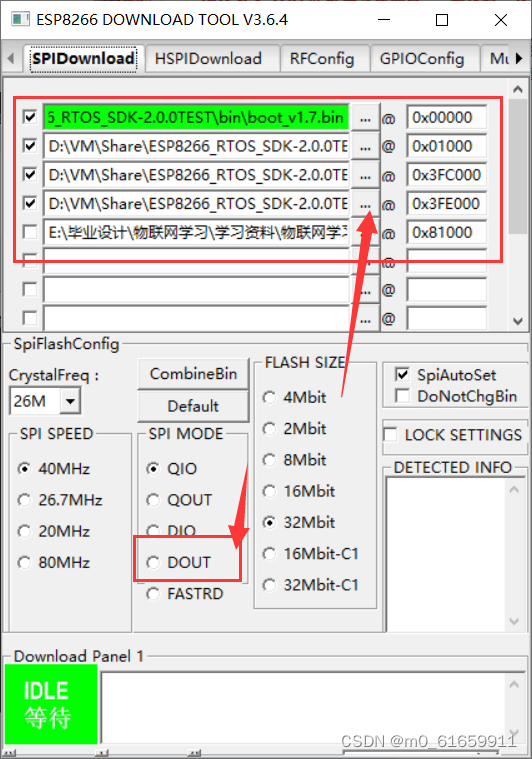
7.wifi开发【智能家居:终】,实践总结:智能开关,智能采集温湿,智能灯。项目运行步骤与运行细节,技术归纳与提炼,项目扩展
一。项目运行步骤与运行细节 1.项目运行步骤(一定有其他的运行方式,我这里只提供一种我现在使用的编译方式) (1)项目运行使用软件与技术: 1.Virtual linux 使用这个虚拟机进行程序的编译 2.Makefile与shl…...

学习开发一个RISC-V上的操作系统(汪辰老师) — unrecognized opcode `csrr t0,mhartid‘报错问题
前言 (1)此系列文章是跟着汪辰老师的RISC-V课程所记录的学习笔记。 (2)该课程相关代码gitee链接; (3)PLCT实验室实习生长期招聘:招聘信息链接 正文 (1)在跟着…...

【计算机网络】 心跳机制
文章目录 心跳机制应用场景什么是心跳机制心跳包的发送,通常有两种技术 心跳机制 应用场景 在长连接下,有可能很长一段时间没有数据往来。理论上说,这个连接是一直保持连接的,但是实际情况中,如果中间节点出现什么故…...

文心一言 VS 讯飞星火 VS chatgpt (106)-- 算法导论10.1 4题
四、用go语言,重写 ENQUEUE 和 DEQUEUE 的代码,使之能处理队列的下溢和上溢。 文心一言: 在 Go 语言中,我们可以使用切片来实现队列。下面是如何实现 ENQUEUE 和 DEQUEUE 操作,同时处理队列的下溢和上溢的情况&#…...

进程调度算法之时间片轮转调度(RR),优先级调度以及多级反馈队列调度
1.时间片轮转调度算法(RR) round Robin 1.算法思想 公平地、轮流地为各个进程服务,让每个进程在一定时间间隔内都可以得到响应。 2.算法规则 按照各进程到达就绪队列的顺序,轮流让各个进程执行一个时间片(如100ms)。 若进程未…...
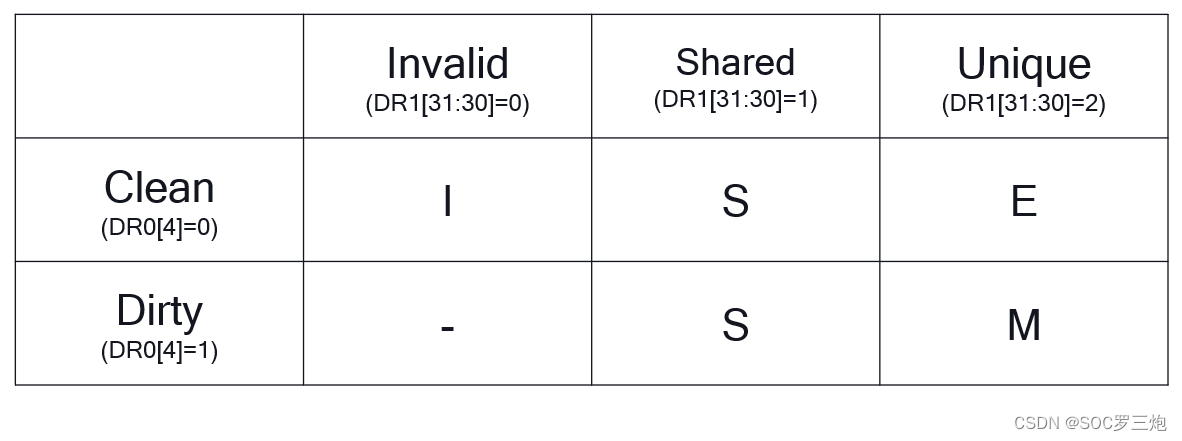
ARMv8如何读取cache line中MESI 状态以及Tag信息(tag RAM dirty RAM)并以Cortex-A55示例
Cortex-A55 MESI 状态获取 一,系统寄存器以及读写指令二,Cortex-A55 Data cache的MESI信息获取(AARCH 64)2.1 将Set/way信息写入Data Cache Tag Read Operation Register2.2 读取Data Register 1和Data Register 0数据并解码 参考…...
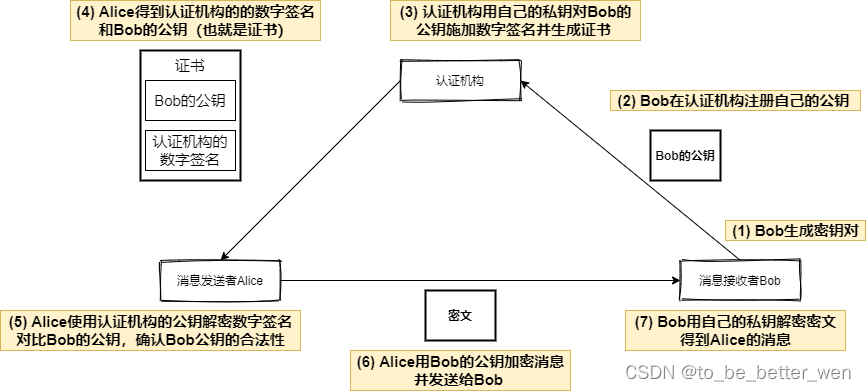
密码技术 (6) - 证书
一. 前言 前面介绍的公钥密码和数字签名,都无法解决一个问题,那就是判断自己获取的公钥是否期望的,不能确定公钥是否被中间攻击人掉包。所以,证书的作用是用来证明公钥是否合法的。本文介绍的证书就是解决证书的可靠性的技术。 二…...
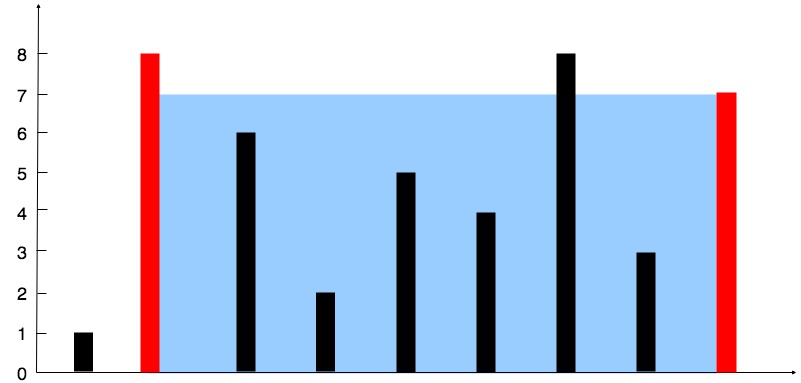
【算法学习】-【双指针】-【盛水最多的容器】
LeetCode原题链接:盛水最多的容器 下面是题目描述: 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。 找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。…...

JAVA面经整理(8)
一)为什么要有区,段,页? 1)页是内存和磁盘之间交互的基本单位内存中的值修改之后刷到磁盘的时候还是以页为单位的索引结构给程序员提供了高效的索引实现方式,不过索引信息以及数据记录都是记录在文件上面的,确切来说是…...

【Java 进阶篇】JDBC数据库连接池Druid详解
在Java应用程序中,与数据库进行交互是一个常见的任务。为了更有效地管理数据库连接并提高性能,数据库连接池是一种常见的解决方案。Druid是一个流行的JDBC数据库连接池,它具有丰富的功能和高性能。本博客将详细介绍Druid连接池,包…...

Linux——指令初识
Linux下基本指令 前言一、 ls 指令二、 pwd命令三、cd 指令四、 touch指令五、mkdir指令六、rmdir指令 && rm 指令七、man指令八、cp指令九、mv指令十、cat指令十一、.more指令十二、less指令十三、head指令十四、tail指令总结 前言 linux的学习开始啦! 今…...
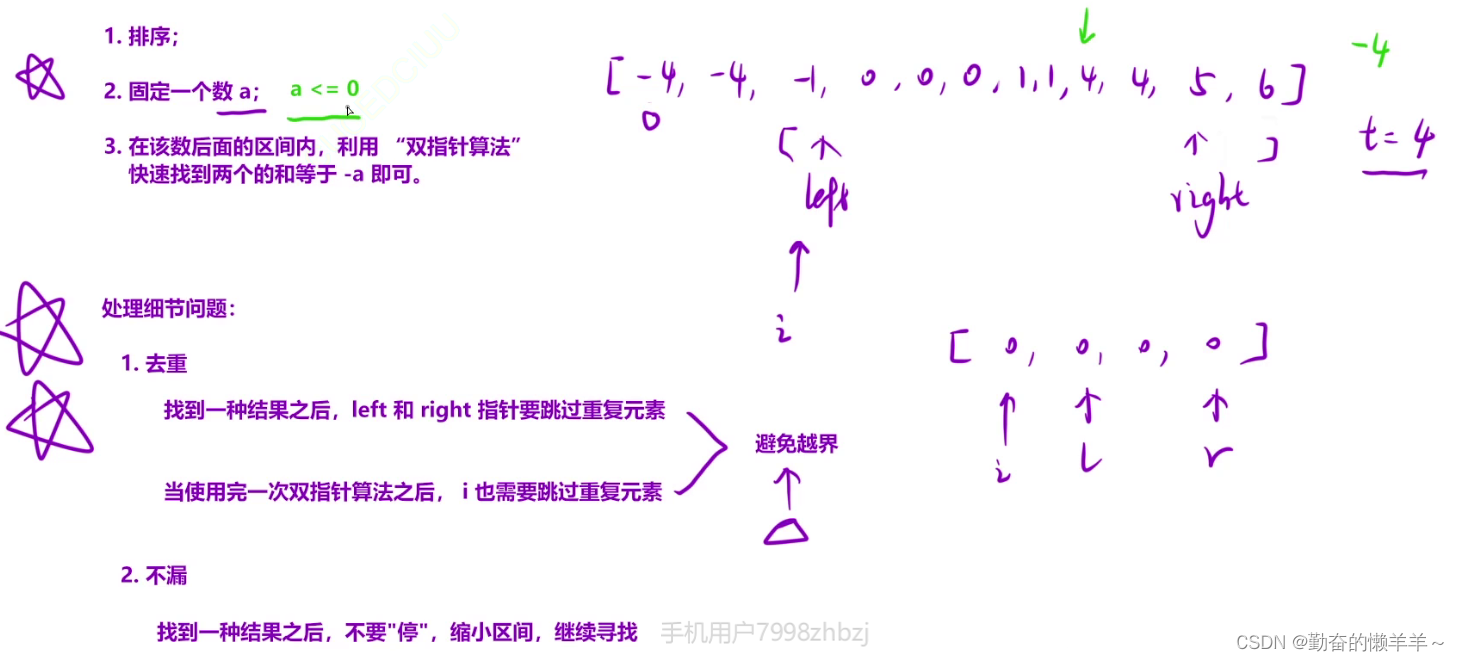
专题一:双指针【优选算法】
双指针应用场景: 数组划分、数组分块 目录 一、移动0 二、复写0 从后向前 三、快乐数 链表带环 四、盛水最多的容器 单调性双指针 五、有效三角形个数 单调性双指针 六、和为s的两个数字 七、三数之和 细节多 需再练 一、移动0 class Solution { public:void move…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...
