【数据结构】布隆过滤器
布隆过滤器的提出
在注册账号设置昵称的时候,为了保证每个用户昵称的唯一性,系统必须检测你输入的昵称是否被使用过,这本质就是一个key的模型,我们只需要判断这个昵称被用过,还是没被用过。
- 方法一:用红黑树或哈希表将所有使用过的昵称存储起来,当需要判断一个昵称是否被用过时,直接判断该昵称是否在红黑树或哈希表中即可。但红黑树和哈希表最大的问题就是浪费空间,当昵称数量非常多的时候内存当中根本无法存储这些昵称
- 方法二:用位图将所有使用过的昵称存储起来,虽然位图只能存储整型数据,但我们可以通过一些哈希算法将字符串转换成整型,比如BKDR哈希算法。当需要判断一个昵称是否被用过时,直接判断位图中该昵称对应的比特位是否被设置即可。
位图虽然能够大大节省内存空间,但由于字符串的组合形式太多了,一个字符的取值有256种,而一个数字的取值只有10种,因此无论通过何种哈希算法将字符串转换成整型都不可避免会存在哈希冲突。
这里的哈希冲突就是不同的昵称最终被转换成了相同的整型,此时就可能会引发误判,即某个昵称明明没有被使用过,却被系统判定为已经使用过了,于是就出现了布隆过滤器。
布隆过滤器的概念
布隆过滤器是由布隆(Burton Howard Bloom)在1970年提出的一种紧凑型的、比较巧妙的概率型数据结构,特点是高效地插入和查询。
-
布隆过滤器其实就是位图的一个变形和延申,虽然无法避免存在哈希冲突,但我们可以想办法降低误判的概率。
-
当一个数据映射到位图中时,布隆过滤器会用多个哈希函数将其映射到多个比特位,当判断一个数据是否在位图当中时,需要分别根据这些哈希函数计算出对应的比特位,如果这些比特位都被设置为1则判定为该数据存在,否则则判定为该数据不存在。
-
布隆过滤器使用多个哈希函数进行映射,目的就在于降低哈希冲突的概率,一个哈希函数产生冲突的概率可能比较大,但多个哈希函数同时产生冲突的概率可就没那么大了。
假设布隆过滤器使用三个哈希函数进行映射,那么“张三”这个昵称被使用后位图中会有三个比特位会被置1,当有人要使用“李四”这个昵称时,就算前两个哈希函数计算出来的位置都产生了冲突,但由于第三个哈希函数计算出的比特位的值为0,此时系统就会判定“李四”这个昵称没有被使用过。
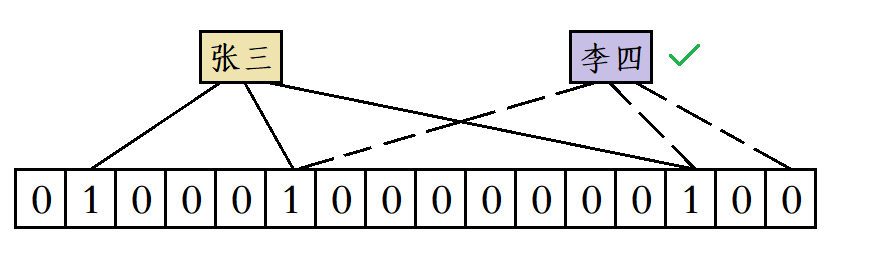
但随着位图中添加的数据不断增多,位图中1的个数也在不断增多,此时就会导致误判的概率增加。
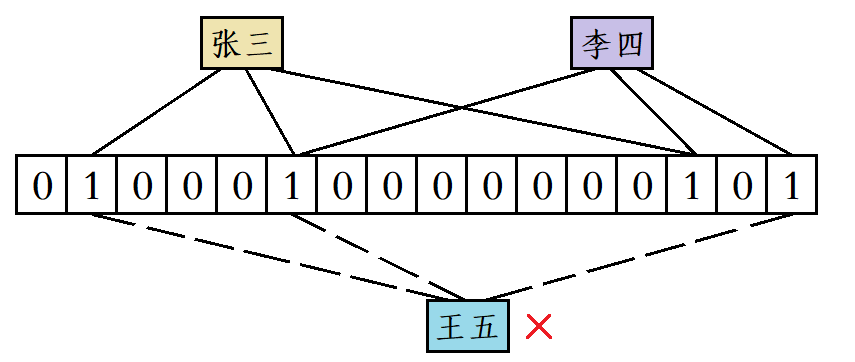
比如“张三”和“李四”都添加到位图中后,当有人要使用“王五”这个昵称时,虽然“王五”计算出来的三个位置既不和“张三”完全一样,也不和“李四”完全一样,但“王五”计算出来的三个位置分别被“张三”和“李四”占用了,此时系统也会误判为“王五”这个昵称已经被使用过了。
布隆过滤器的特点
-
布隆过滤器判断一个数据存在可能是不准确的,因为这个数据对应的比特位可能被其他一个数据或多个数据占用了。
-
布隆过滤器判断一个数据不存在是准确的,因为如果该数据存在那么该数据对应的比特位都应该已经被设置为1了。
如何控制误判率?
-
很显然,过小的布隆过滤器很快所有的比特位都会被设置为1,此时布隆过滤器的误判率就会变得很高,因此布隆过滤器的长度会直接影响误判率,布隆过滤器的长度越长其误判率越小。
-
此外,哈希函数的个数也需要权衡,哈希函数的个数越多布隆过滤器中比特位被设置为1的速度越快,并且布隆过滤器的效率越低,但如果哈希函数的个数太少,也会导致误判率变高。
那应该如何选择哈希函数的个数和布隆过滤器的长度呢,有人通过计算后得出了以下关系式:
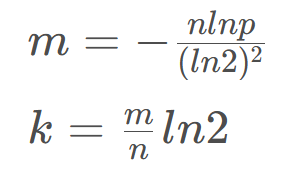
其中k为哈希函数个数,m为布隆过滤器长度,n为插入的元素个数,p为误判率。
我们这里可以大概估算一下,如果使用3个哈希函数,即k的值为3, ln2的值我们取0.7,那么m和n的关系大概是m = 4 * n,也就是布隆过滤器的长度应该是插入元素个数的4倍。
布隆过滤器的实现
首先,布隆过滤器可以实现为一个模板类,因为插入布隆过滤器的元素不仅仅是字符串,也可以是其他类型的数据,只有调用者能够提供对应的哈希函数将该类型的数据转换成整型即可,但一般情况下布隆过滤器都是用来处理字符串的,所以这里可以将模板参数K的缺省类型设置为string。
布隆过滤器中的成员一般也就是一个位图,我们可以在布隆过滤器这里设置一个非类型模板参数N,用于让调用者指定位图的长度。
//布隆过滤器
template<size_t N, class K = string, class Hash1 = BKDRHash, class Hash2 = APHash, class Hash3 = DJBHash>
class BloomFilter {
public://...
private:bitset<N> _bs;
};
实例化布隆过滤器时需要调用者提供三个哈希函数,由于布隆过滤器一般处理的是字符串类型的数据,因此这里我们可以默认提供几个将字符串转换成整型的哈希函数。
- 这里选取将字符串转换成整型的哈希函数,是经过测试后综合评分最高的BKDRHash、APHash和DJBHash,这三种哈希算法在多种场景下产生哈希冲突的概率是最小的。
- 此时本来这三种哈希函数单独使用时产生冲突的概率就比较小,现在要让它们同时产生冲突概率就更小了。
代码如下:
struct BKDRHash {size_t operator()(const string &s) {size_t value = 0;for (auto ch: s) {value = value * 131 + ch;}return value;}
};struct APHash {size_t operator()(const string &s) {size_t value = 0;for (size_t i = 0; i < s.size(); i++) {if ((i & 1) == 0) {value ^= ((value << 7) ^ s[i] ^ (value >> 3));} else {value ^= (~((value << 11) ^ s[i] ^ (value >> 5)));}}return value;}
};struct DJBHash {size_t operator()(const string &s) {if (s.empty())return 0;size_t value = 5381;for (auto ch: s) {value += (value << 5) + ch;}return value;}
};
布隆过滤器的插入
布隆过滤器当中需要提供一个Set接口,用于插入元素到布隆过滤器当中。插入元素时,需要通过三个哈希函数分别计算出该元素对应的三个比特位,然后将位图中的这三个比特位设置为1即可。
代码如下:
void Set(const K &key) {//计算出key对应的三个位size_t i1 = Hash1()(key) % N;size_t i2 = Hash2()(key) % N;size_t i3 = Hash3()(key) % N;//设置位图中的这三个位_bs.set(i1);_bs.set(i2);_bs.set(i3);
}
布隆过滤器的查找
布隆过滤器当中还需要提供一个Test接口,用于检测某个元素是否在布隆过滤器当中。检测时,需要通过三个哈希函数分别计算出该元素对应的三个比特位,然后判断位图中的这三个比特位是否被设置为1。
- 只要这三个比特位当中有一个比特位未被设置则说明该元素一定不存在。
- 如果这三个比特位全部被设置,则返回true表示该元素存在(可能存在误判)。
代码如下:
bool Test(const K &key) {//依次判断key对应的三个位是否被设置size_t i1 = Hash1()(key) % N;if (_bs.test(i1) == false) {return false;//key一定不存在}size_t i2 = Hash2()(key) % N;if (_bs.test(i2) == false) {return false;//key一定不存在}size_t i3 = Hash3()(key) % N;if (_bs.test(i3) == false) {return false;//key一定不存在}return true;//key对应的三个位都被设置,key存在(可能误判)
}
布隆过滤器的删除
布隆过滤器一般不支持删除操作,原因如下:
- 因为布隆过滤器判断一个元素存在时可能存在误判,因此无法保证要删除的元素确实在布隆过滤器当中,此时将位图中对应的比特位清0会影响其他元素。
- 此外,就算要删除的元素确实在布隆过滤器当中,也可能该元素映射的多个比特位当中有些比特位是与其他元素共用的,此时将这些比特位清0也会影响其他元素。
如何让布隆过滤器支持删除?
要让布隆过滤器支持删除,必须要做到以下两点:
- 保证要删除的元素在布隆过滤器当中。比如刚才的呢称例子当中,如果通过调用Test函数得知要删除的昵称可能存在布隆过滤器当中后,可以进一步遍历存储昵称的文件,确认该昵称是否真正存在。
- 保证删除后不会影响到其他元素。可以为位图中的每一个比特位设置一个对应的计数值,当插入元素映射到该比特位时将该比特位的计数值++,当删除元素时将该元素对应比特位的计数值–即可。
可是布隆过滤器最终还是没有提供删除的接口,因为使用布隆过滤器本来就是要节省空间和提高效率的。在删除时需要遍历文件或磁盘中确认待删除元素确实存在,而文件IO和磁盘IO的速度相对内存来说是很慢的,并且为位图中的每个比特位额外设置一个计数器,就需要多用原位图几倍的存储空间,这个代价也是不小的。
布隆过滤器的优点
-
增加和查询元素的时间复杂度为O(K)(K为哈希函数的个数,一般比较小),与数据量大小无关。
-
哈希函数相互之间没有关系,方便硬件并行运算。
-
布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势。
-
在能够承受一定的误判时,布隆过滤器比其他数据结构有着很大的空间优势。
-
数据量很大时,布隆过滤器可以表示全集,其他数据结构不能。
-
使用同一组哈希函数的布隆过滤器可以进行交、并、差运算。
布隆过滤器的缺陷
- 有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再自建一个白名单,存储可能会误判的数据)
- 不能获取元素本身。
- 一般情况下不能从布隆过滤器中删除元素。
布隆过滤器使用场景
使用布隆过滤器的前提是,布隆过滤器的误判不会对业务逻辑造成影响。
比如当我们首次访问某个网站时需要用手机号注册账号,而用户的各种数据实际都是存储在数据库当中的,也就是磁盘上面。
- 当我们用手机号注册账号时,系统就需要判断你填入的手机号是否已经注册过,如果注册过则会提示用户注册失败。
- 但这种情况下系统不可能直接去遍历磁盘当中的用户数据,判断该手机号是否被注册过,因为磁盘IO是很慢的,这会降低用户的体验。
- 这种情况下就可以使用布隆过滤器,将所有注册过的手机号全部添加到布隆过滤器当中,当我们需要用手机号注册账号时,就可以直接去布隆过滤器当中进行查找。
- 如果在布隆过滤器中查找后发现该手机号不存在,则说明该手机号没有被注册过,此时就可以让用户进行注册,并且避免了磁盘IO。
- 如果在布隆过滤器中查找后发现该手机号存在,此时还需要进一步访问磁盘进行复核,确认该手机号是否真的被注册过,因为布隆过滤器在判断元素存在时可能会误判。
由于大部分情况下用户用一个手机号注册账号时,都是知道自己没有用该手机号注册过账号的,因此在布隆过滤器中查找后都是找不到的,此时就避免了进行磁盘IO。而只有布隆过滤器误判或用户忘记自己用该手机号注册过账号的情况下,才需要访问磁盘进行复核。
以让用户进行注册,并且避免了磁盘IO。
- 如果在布隆过滤器中查找后发现该手机号存在,此时还需要进一步访问磁盘进行复核,确认该手机号是否真的被注册过,因为布隆过滤器在判断元素存在时可能会误判。
由于大部分情况下用户用一个手机号注册账号时,都是知道自己没有用该手机号注册过账号的,因此在布隆过滤器中查找后都是找不到的,此时就避免了进行磁盘IO。而只有布隆过滤器误判或用户忘记自己用该手机号注册过账号的情况下,才需要访问磁盘进行复核。
相关文章:
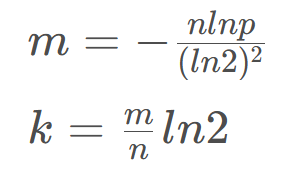
【数据结构】布隆过滤器
布隆过滤器的提出 在注册账号设置昵称的时候,为了保证每个用户昵称的唯一性,系统必须检测你输入的昵称是否被使用过,这本质就是一个key的模型,我们只需要判断这个昵称被用过,还是没被用过。 方法一:用红黑…...

linux基础4---内存
1、什么是内存泄漏,怎么解决内存泄漏? 在嵌入式Linux中,内存泄漏是指由于疏忽或错误,导致一些对象或资源无法被垃圾回收器回收,从而导致内存占用不断增加,最终导致设备性能下降。内存泄漏对程序的影响很大,可能会导致应用程序变慢、崩溃或者消耗大量的内存,最终导致设…...

图论---拓扑排序
概念 一个有向图,如果图中有入度为 0 的点,就把这个点删掉,同时也删掉这个点所连的边。一直进行上面的处理,如果所有点都能被删掉,则这个图可以进行拓扑排序。拓扑排序是对DAG(有向无环图)上的节…...
java Spring Boot 将日志写入文件中记录
我们之前的一套操作来讲 日志都是在控制台上的 但 如果你的项目在正式环境上跑 运维人员突然告诉你说日志报错了,但你日志只在控制台上,那公司项目如果访问量很大 那你是很难在控制台上找到某一条日志的 这时 我们就可以用文件把它记下来 我们打开项目 …...
Android 开发错误集合
🔥 开发错误集合一 🔥 Caused by: java.lang.ClassNotFoundException: Didnt find class "com.mask.app.ui.LoginRegisterActivity" on path: DexPathList[[zip file "/data/app/~~NMvHVhj8V6-HwGbh2amXDA/com.mask.app-PWbg4xIlETQ3eVY…...

VSCode个人设置习惯
账号登陆同步 点击左下角齿轮或者用户头像–>Turn on Settings Sync–>全选–>Sign in &Turn on。 可以同步配置、快捷键、插件、用户代码片段、UI状态 Windows下将powershell改为cmd 在vscode打开集成终端,点击右上角加号右边的下拉菜单,…...
 322. 零钱兑换 279.完全平方数)
代码随想录训练营二刷第四十七天 | 70. 爬楼梯 (进阶) 322. 零钱兑换 279.完全平方数
代码随想录训练营二刷第四十七天 | 70. 爬楼梯 (进阶) 322. 零钱兑换 279.完全平方数 一、70. 爬楼梯 (进阶) 题目链接:https://leetcode.cn/problems/climbing-stairs/ 思路:物品是楼梯1和2,…...
beego-简单项目写法--后续放到git上
Beego案例-新闻发布系统 1.注册 后台代码和昨天案例代码一致。,所以这里面只写一个注册的业务流程图。 **业务流程图 ** 2.登陆 业务流程图 登陆和注册业务和我们昨天登陆和注册基本一样,所以就不再重复写这个代码 但是我们遇到的问题是如何做代码的迁移&…...
【算法|动态规划No.9】leetcodeLCR 091. 粉刷房子
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...
基于SpringBoot的图书进销存管理系统
目录 前言 一、技术栈 二、系统功能介绍 用户信息管理 图书类型管理 商品退货管理 客户信息管理 图书添加 客户添加 应收金额 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实…...

回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测
回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测 目录 回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测预测效果基本介绍模型描述程序设计预测效果 <...

vue3使用v-model控制子组件进行双向数据绑定
vue2写法: 中父组件调用子组件: <child :isShow.sync"isShow" v-show"isShow"/> 子组件想要消失, 在子组件写: this.$emit("update:isShow",false); 具体代码就不粘贴了 vue3写法: 父组件核心代码: v-model:a"xxx" 子组…...

.netCore .net5,6,7 存日志文件
如果你使用 .netCore及以上版本(.net5,.net6,.net7)... 系统默认自带日志中间件(log4net) 对,就是上次java 日志大漏洞的兄弟....... 控制台自动打印日志就是它的功劳 现在我们想存日志文件,怎么办 很简单. 1.在项目中添加日志配置文件 文件名 : log4net.config 不能…...
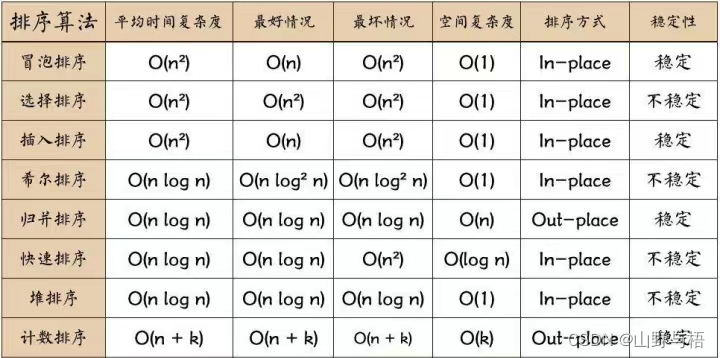
【数据结构---排序】很详细的哦
本篇文章介绍数据结构中的几种排序哦~ 文章目录 前言一、排序是什么?二、排序的分类 1.直接插入排序2.希尔排序3.选择排序4.冒泡排序5.快速排序6.归并排序总结 前言 排序在我们的生活当中无处不在,当然,它在计算机程序当中也是一种很重要的操…...
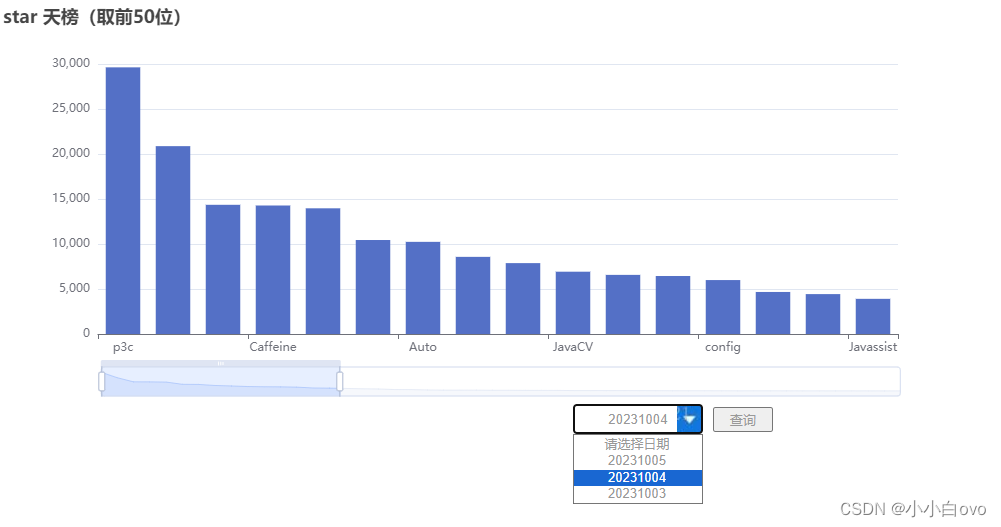
GitHub爬虫项目详解
前言 闲来无事浏览GitHub的时候,看到一个仓库,里边列举了Java的优秀开源项目列表,包括说明、仓库地址等,还是很具有学习意义的。但是大家也知道,国内访问GitHub的时候,经常存在访问超时的问题,…...
-NOA领航辅助系统-上汽荣威)
辅助驾驶功能开发-功能对标篇(7)-NOA领航辅助系统-上汽荣威
1.横向对标参数 厂商上汽荣威车型荣威RX5(燃油车)上市时间2022Q3方案10V3R摄像头前视摄像头1*(8M)侧视摄像头4后视摄像头1环视摄像头4DMS摄像头1雷达毫米波雷达34D毫米波雷达/超声波雷达12激光雷达/域控供应商1*(宏景智驾)辅助驾驶软件供应商地平线高精度地图中海庭芯片J3合作…...

第0次 序言
突然想起有好多书没有看,或者看了也没留下任何记录,以后有空必须得好好整理才行,这次就从《Linux命令行和shell脚本编程大全开始》 本文完全是闲聊,自娱自乐,我觉得做开发是一件很快乐的事情,但是工作是开发…...

ESP32设备驱动-OLED显示单个或多个DS18B20传感器数据
OLED显示单个或多个DS18B20传感器数据 文章目录 OLED显示单个或多个DS18B20传感器数据1、DS18B20介绍2、硬件准备3、软件准备4、代码实现4.1 读取单个DS18B20数据4.2 驱动多个DS18B20传感器4.3 OLED显示DS18B20数据在本文中,我们将介绍如何ESP32驱动单个或多个DS18B20传感器,…...
MongoDB快速上手
文章目录 1、mongodb相关概念1.1、业务应用场景1.2、MongoDB简介1.3、体系结构1.3.1 数据库 (databases) 管理语法1.3.2 集合 (collection) 管理语法 1.4、数据模型1.5、MongoDB的特点 2、单机部署3、基本常用命令3.1、案例需求3.2、数据库操作3.2.1 选择和创建数据库3.2.2 数据…...
maven 初学
1. maven 安装 配置安装 路径 maven 下载位置: D:\software\apache-maven-3.8.6 默认仓库位置: C:\Users\star-dream\.m2\repository 【已更改】 本地仓库设置为:D:\software\apache-maven-3.8.6\.m2\repository 镜像已更改为阿里云中央镜像仓库 <mirrors>…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
