【做题笔记】多项式/FFT/NTT
HDU1402 - A * B Problem Plus
题目链接
大数乘法是多项式的基础应用,其原理是将多项式 f ( x ) = a 0 + a 1 x + a 2 x 2 + a 3 x 3 + ⋯ + a n x n f(x)=a_0+a_1x+a_2x^2+a_3x^3+\cdots+a_nx^n f(x)=a0+a1x+a2x2+a3x3+⋯+anxn中的 x = 10 x=10 x=10,然后让大数的每一位当做对应的 1 0 y 10^y 10y的系数,然后进行多项式乘法运算,以降低大数乘法的时间复杂度(高精度乘法时间复杂度是 O ( n 2 ) O(n^2) O(n2)的,多项式乘法是 O ( n log n ) O(n\log n) O(nlogn), n n n是位数)。
在进行多项式乘法之后,我们得到了新的多项式 h ( x ) = c 0 + c 1 × 10 + c 2 × 1 0 2 + ⋯ + c m × 1 0 m h(x)=c_0+c_1\times 10+c_2\times 10^2+\cdots + c_m\times 10^m h(x)=c0+c1×10+c2×102+⋯+cm×10m。
这里的 c 0 , c 1 , ⋯ , c m c_0,c_1,\cdots,c_m c0,c1,⋯,cm由于在乘法时会发生进位,所以每一位可能会大于 9 9 9,此时要将后面的位的值挪到下一位上去,让这一位保证在 9 9 9以内。
然后从高位到低位找到第一个不是 0 0 0的位,然后逐位输出即可。
如果最终结果是 0 0 0,要特别判断。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod = (1ll << 47) * 7 * 4451 + 1;
const LL g = 3;LL mul(LL x, LL y) {return (x * y - (LL)(x / (long double)mod * y + 1e-3) * mod + mod) % mod;
}template<class T> T power(T a, LL b) {T res = 1;for (; b; b >>= 1) {if (b & 1) res = mul(res, a);a = mul(a, a);}return res;
}LL rev[4000005];void change(LL *y, int len) {for (int i = 0; i < len; ++i) {if (i < rev[i]) swap(y[i], y[rev[i]]);}
}void DFT(LL *y, int len, int on) {change(y, len);for (LL h = 2; h <= len; h <<= 1) {LL wn = power(g, (mod - 1) / h);if (on == -1) wn = power(wn, mod - 2); for (int j = 0; j < len; j += h) {LL w = 1ll;for (int k = j; k < j + h / 2; ++k) {LL u = y[k] % mod;LL t = mul(w, y[k + h / 2]);y[k] = (u + t) % mod;y[k + h / 2] = (u - t + mod) % mod;w = mul(w, wn);}}}
}void NTT(LL *x1, LL *x2, LL len) {for (int i = 0; i < len; ++i) {rev[i] = rev[i >> 1] >> 1;if (i & 1) rev[i] |= len >> 1;}DFT(x1, len, 1);DFT(x2, len, 1);for (int i = 0; i < len; ++i) {x1[i] = mul(x1[i], x2[i]);}DFT(x1, len, -1);LL inv = power(len, mod - 2);for (int i = 0; i < len; ++i) {x1[i] = mul(x1[i], inv);}
}string a, b;
LL x1[2000005], x2[2000005];void main2() {cin >> b;int n = a.length(), m = b.length();int len = 1;while (len <= (n + m) * 2 + 1) len <<= 1;int pt = n - 1;for (char c: a) {x1[pt--] = c - '0';}for (int i = n; i < len + 300; ++i) {x1[i] = 0;}pt = m - 1;for (char c: b) {x2[pt--] = c - '0';}for (int i = m; i < len; ++i) {x2[i] = 0;}NTT(x1, x2, len);for (int i = 0; i < len; ++i) {if (x1[i] > 9) {x1[i + 1] += (x1[i] / 10);x1[i] %= 10;}}pt = len;while (x1[pt] > 0) {if (x1[pt] > 9) {x1[pt + 1] += (x1[pt] / 10);x1[pt++] %= 10;}}while (pt >= 0 and x1[pt] == 0) --pt;if (pt == -1) {cout << 0 << '\n';return;}for (int i = pt; i >= 0; --i) {cout << x1[i];}cout << '\n';
}int main() {ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);LL _ = 1;
// cin >> _;while (cin >> a) main2();return 0;
}
HDU4609 - 3-idiots
题目链接
要求能够成三角形的概率,我们可以通过可以构成三角形的情况总数/总的情况数来得到。其中总的情况数就是 ( n 3 ) \binom{n}{3} (3n),重点是求解可以构成三角形的情况。
首先我们可以维护一个多项式, x i x_i xi的系数表示长度为 i i i的线段有多少条。那么以样例 1 1 1为例,得到的多项式的系数就是: [ 0 , 1 , 0 , 2 , 1 ] [0,1,0,2,1] [0,1,0,2,1]。
接下来,我们将这个多项式自己与自己相乘,也就是 [ 0 , 1 , 0 , 2 , 1 ] × [ 0 , 1 , 0 , 2 , 1 ] [0,1,0,2,1]\times [0,1,0,2,1] [0,1,0,2,1]×[0,1,0,2,1],得到的多项式的系数是: [ 0 , 0 , 1 , 0 , 4 , 2 , 4 , 4 , 1 ] [0,0,1,0,4,2,4,4,1] [0,0,1,0,4,2,4,4,1]。
这个多项式表示的含义是从第一个 [ 0 , 1 , 0 , 2 , 1 ] [0,1,0,2,1] [0,1,0,2,1]取出一个边,从第二个 [ 0 , 1 , 0 , 2 , 1 ] [0,1,0,2,1] [0,1,0,2,1]取出一个边:
取出两个边的长度和为 0 0 0的有 0 0 0种;
取出两个边的长度和为 1 1 1的有 0 0 0种;
取出两个边的长度和为 2 2 2的有 1 1 1种;
取出两个边的长度和为 3 3 3的有 0 0 0种;
取出两个边的长度和为 4 4 4的有 4 4 4种;
取出两个边的长度和为 5 5 5的有 2 2 2种;
取出两个边的长度和为 6 6 6的有 4 4 4种;
取出两个边的长度和为 7 7 7的有 4 4 4种;
取出两个边的长度和为 8 8 8的有 1 1 1种。
我们现在要利用得到的这个信息来求解答案。
我们先来看一看我们的三条边形成三角形,有怎样的条件:设三角形三条边是 a , b , c a,b,c a,b,c,且 a < b < c a<b<c a<b<c。于是有 a + b > c a+b>c a+b>c。
首先,在我们得到的 [ 0 , 0 , 1 , 0 , 4 , 2 , 4 , 4 , 1 ] [0,0,1,0,4,2,4,4,1] [0,0,1,0,4,2,4,4,1]中,存在同一条边被采用两次的情况,首先我们要遍历每一条边,将长度之和为其二倍的情况 − 1 -1 −1。原始的 4 4 4条边的边长分别是 [ 1 , 3 , 3 , 4 ] [1,3,3,4] [1,3,3,4],所以我们要减去两条边长度为 [ 2 , 6 , 6 , 8 ] [2,6,6,8] [2,6,6,8]的一种方案。于是变成: [ 0 , 0 , 0 , 0 , 4 , 2 , 2 , 4 , 0 ] [0,0,0,0,4,2,2,4,0] [0,0,0,0,4,2,2,4,0]。
然后,由于我们两边的边是一样的,左边取 a a a右面取 b b b,左边取 b b b右边取 a a a,这两种其实应当是一种方案。所以我们应当将每一个可能的两边长度的可能情况减半。于是变成 [ 0 , 0 , 0 , 0 , 2 , 1 , 1 , 2 , 0 ] [0,0,0,0,2,1,1,2,0] [0,0,0,0,2,1,1,2,0]。
如果我们设最终答案为 t o t a l total total,将卷积后得到的结果求一个前缀和叫做 p r e pre pre, n n n条边最长的那条边为 m x mx mx。先将所有边从小到大进行排序。
接下来依次枚举 n n n条边,对于第 i i i条边,我们设其长度为 c i c_i ci,并认定其为最长边的情况,求解这种情况时的可行方案数。首先,根据两边之和大于第三边,我们剩下两条边的长度之和应当大于 c i c_i ci,所以从刚刚卷积和处理后得到的信息中,将长度之和为 [ c i + 1 , ∞ ] [c_i+1,\infty] [ci+1,∞]的可能情况加到答案中。
那么这一步就是 t o t a l ← t o t a l + p r e [ 2 m x ] − p r e [ c i ] total\leftarrow total+pre[2mx]-pre[c_i] total←total+pre[2mx]−pre[ci]。
然后根据我们刚才所设,当前边我们令其为最大边,所以一切包含一个小于 c i c_i ci的边、包含一个大于 c i c_i ci的边都是不合法的,但是因为这两条边的长度和一定大于 c i c_i ci,所以被算进了 t o t a l total total里面,所以要从 t o t a l total total里面减掉。我们考虑这样的可能发生情况是 ( n − i ) × ( i − 1 ) (n-i)\times (i-1) (n−i)×(i−1),其中 n − i n-i n−i是比 c i c_i ci长的边的数量, i − 1 i-1 i−1是比 c i c_i ci短的数量和。
这一步就是 t o t a l ← t o t a l − ( n − i ) × ( i − 1 ) total\leftarrow total-(n-i)\times(i-1) total←total−(n−i)×(i−1)。
还有一种情况,就是两条边都取了比 c i c_i ci长的,那就是 ( n − i 2 ) \binom{n-i}{2} (2n−i)种情况,因为是从比 c i c_i ci长的 n − i n-i n−i个边里任意挑选两个边。
这一步就是 t o t a l ← t o t a l − ( n − i 2 ) total\leftarrow total-\binom{n-i}{2} total←total−(2n−i)。
还有一种情况,就是一条边取了自身,另一条边取了其他,存在 n − 1 n-1 n−1种情况。这里因为之前已经除以 2 2 2,所以不用考虑从哪里搬来的情况。
这一步就是 t o t a l ← t o t a l − ( n − 1 ) total\leftarrow total-(n-1) total←total−(n−1)。
将 n n n条边对 t o t a l total total的贡献全部计算一遍之后,最后的结果就是所有合法的情况数了。
最后的答案就是 t o t a l ( n 3 ) \frac{total}{\binom{n}{3}} (3n)total。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100005;
const LL mod = 998244353;
const LL g = 3, gi = 332748118;
const double PI = acos(-1.0);struct Complex {double x, y;Complex(double _x = 0.0, double _y = 0.0) {x = _x; y = _y;}Complex operator - (const Complex &b) const {return Complex(x - b.x, y - b.y);}Complex operator + (const Complex &b) const {return Complex(x + b.x, y + b.y);}Complex operator * (const Complex &b) const {return Complex(x * b.x - y * b.y, x * b.y + y * b.x);}
};LL rev[4000005];void change(Complex *y, int len) {for (int i = 0; i < len; ++i) {if (i < rev[i]) swap(y[i], y[rev[i]]);}
}void FFT(Complex *y, int len, int on) {change(y, len);for (int h = 2; h <= len; h <<= 1) {Complex wn(cos(2 * PI / h), sin(on * 2 * PI / h));for (int j = 0; j < len; j += h) {Complex w(1, 0);for (int k = j; k < j + h / 2; ++k) {Complex u = y[k];Complex t = w * y[k + h / 2];y[k] = u + t;y[k + h / 2] = u - t;w = w * wn;}}}if (on == -1) {for (int i = 0; i < len; ++i) {y[i].x = y[i].x / len + 0.5;}}
}LL n, len = 289999;
LL a[N], x[N * 3], pre[N * 2];
Complex F[N * 2];void main2() {cin >> n;LL mx = 0;memset(x, 0, sizeof(x));for (int i = 1; i <= n; ++i) {cin >> a[i];mx = max(mx, a[i]);++x[a[i]];}len = 1;while (len <= mx * 2 + 1) len <<= 1;for (int i = 0; i <= mx; ++i) {F[i].x = (double)x[i];F[i].y = 0;}for (int i = mx + 1; i < len; ++i) {F[i].x = F[i].y = 0;}for (int i = 0; i < len; ++i) {rev[i] = rev[i >> 1] >> 1;if (i & 1) rev[i] |= len >> 1;}FFT(F, len, 1);for (int i = 0; i < len; ++i) {F[i] = (F[i] * F[i]);}FFT(F, len, -1);for (int i = 0; i < len; ++i) {x[i] = (LL)F[i].x;}for (int i = 1; i <= n; ++i) {--x[a[i] * 2];}for (int i = 1; i <= mx * 2; ++i) {x[i] /= 2;}pre[0] = 0;for (int i = 1; i <= mx * 2; ++i) {pre[i] = pre[i - 1] + x[i];}LL total = 0;for (LL i = 1; i <= n; ++i) {total += (pre[mx * 2] - pre[a[i]]);total -= ((n - i) * (i - 1));total -= (n - 1);total -= ((n - i) * (n - i - 1) / 2);}LL all = n * (n - 1) * (n - 2) / 6;double ans = (double)total / (double)all;cout << fixed << setprecision(7) << ans << '\n';
}int main() {ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);LL _ = 1;cin >> _;while (_--) main2();return 0;
}
CF954I - Yet Another String Matching Problem
题目链接
首先考虑,如果 S S S串和 T T T串长度相同,该怎么做。我们发现,我们的目的是消除差异性,即对于上下每一对字母,他们最后都要变成同一个字母。
以abcd和ddcb为例,那么上下每一对依次是a-d,b-d,c-c,d-b。我们将每一个字母设为一个点,将每一对当做一个边连起来,连完之后长这个样子:
会发现几个字母会连成一个连通图:
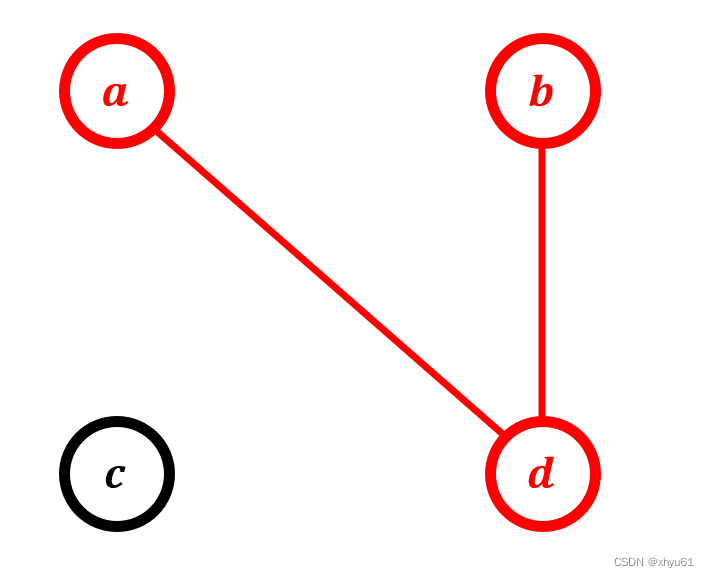
我们将四个字母分为了两个部分: c c c自己是一个部分, a b d abd abd三个字母是一个部分。我们发现,连的边指在原来的两个串中对应的同一个位置的两个字母,他们最终要变成同一个字母。而每一次操作要同时改变两个串中的这个字母,所以我们不难推出,被我们连上边形成连通块的这些字母,他们最后必然要变成同一个字母。我们就让他变成他们之中的一个字母,那么我们发现,其实我们的操作数,就是我们连的边的数量,因为我们每连一次边,就相当于要进行一次题目中的操作,变换一个字母。
这样我们用并查集来实现:对于每一个位置,判断这个位置的两个字母是否相同,如果相同那就不需要我们动了;如果不同,就需要判断这两个字母现在是否在一个连通块,如果在,则不管(已经变成同样的字母了),不在同一个连通块就用并查集合并一下,然后答案 + 1 +1 +1。
因为我们的字符集只有前 6 6 6个字母 a b c d e f abcdef abcdef,所以合并操作这类的都是常数级别。那么,在两个串长度相等的情况下,得到答案的时间复杂度是 O ( m ) O(m) O(m)的。
但是我们原题中 S S S串会比较长,我们需要枚举每一个长度为 ∣ T ∣ \vert T\vert ∣T∣的子串,每个子串都要求一次答案,于是时间复杂度变成 O ( n m ) O(nm) O(nm)的了,直接爆炸。
我们来尝试进行一波优化,看看哪里是最消耗时间的地方。
我们注意到,我们的字符串长度的规模是 1.25 × 1 0 5 1.25\times 10^5 1.25×105,而我们的字符集大小只有 6 6 6,意味着我们同一个位置可能的字符对只有 6 × 36 6\times 36 6×36种。又由于我们不考虑上下相同的字符串,所以我们需要考虑的字符对情况只有 36 − 6 = 30 36-6=30 36−6=30种。对于一次子串和 T T T串的求解过程中,如果串过长,那么相同的字符对会出现很多次,而其中只有一次是有用的,在第一次的时候我们对这两个字母进行连边,从第二次开始再遇到这个字符对,根本就是毫无用处了。所以,如果我们能够判断出,每一个子串跟 T T T串匹配的过程中,所有位里是否包含这样的字符对就好了。
怎么来做?先说结论:用到卷积。
先来看一个关于卷积的性质。假设我们有两个多项式:
f ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a n x n f(x)=a_0+a_1x+a_2x^2+\cdots+a_nx^n f(x)=a0+a1x+a2x2+⋯+anxn
g ( x ) = b 0 + b 1 x + b 2 x 2 + ⋯ + b n x n g(x)=b_0+b_1x+b_2x^2+\cdots+b_nx^n g(x)=b0+b1x+b2x2+⋯+bnxn
试求 f ( x ) ⋅ g ( x ) f(x)\cdot g(x) f(x)⋅g(x)。
我们发现, f ( x ) ⋅ g ( x ) = a 0 b 0 + ( a 0 b 1 + a 1 b 0 ) x + ( a 0 b 2 + a 1 b 1 + a 2 b 0 ) x 2 + ( a 0 b 3 + a 1 b 2 + a 2 b 1 + a 3 b 0 ) x 3 + ⋯ f(x)\cdot g(x)=a_0b_0+(a_0b_1+a_1b_0)x+(a_0b_2+a_1b_1+a_2b_0)x^2+(a_0b_3+a_1b_2+a_2b_1+a_3b_0)x^3+\cdots f(x)⋅g(x)=a0b0+(a0b1+a1b0)x+(a0b2+a1b1+a2b0)x2+(a0b3+a1b2+a2b1+a3b0)x3+⋯
发现了什么?最后得到的多项式系数, x k x^k xk的系数是 ∑ i = 0 k a i b k − i \displaystyle\sum\limits_{i=0}^k a_ib_{k-i} i=0∑kaibk−i,你会发现他们由所有 i + j = k i+j=k i+j=k的 a i b j a_ib_j aibj相加得到,换句话说,组成 x k x^k xk的系数的所有 a i b j a_ib_j aibj,都满足他们的下标和 i + j i+j i+j是定值,且定值为 k k k。
然后看看我们需要的是什么?事实上,我们可以总结出我们现阶段的问题是:从 S S S串的第 i i i位作为第一个字符的长度为 ∣ T ∣ \vert T\vert ∣T∣的子串和 T T T串匹配的过程中,字符 c 1 c_1 c1和字符 c 2 c_2 c2是否出现。
在其中的一个固定了 c 1 c_1 c1和 c 2 c_2 c2的子问题中,我们设一个数组 a i a_i ai,表示 S S S串的第 i i i位是否为 c 1 c_1 c1。如果 a i = 1 a_i=1 ai=1,说明是 c 1 c_1 c1;如果 a i = 0 a_i=0 ai=0,说明第 i i i不是 c 1 c_1 c1。同样的方式设一个数组 b i b_i bi,表示 T T T串第 i i i位是否为 c 2 c_2 c2。
那么, T T T串的第一个字母和 S S S串第 i i i个字母对上的时候,字符对 ( c 1 , c 2 ) (c1,c2) (c1,c2)出现的条件是什么?如果 ∑ k = 0 ∣ T ∣ − 1 a i + k b k > 0 \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_{i+k}b_{k}>0 k=0∑∣T∣−1ai+kbk>0,说明存在这样的字符对 ( c 1 , c 2 ) (c_1,c_2) (c1,c2)。
因为这种情况下, S S S串的第 i + k i+k i+k位和 T T T串的第 k k k是对上的,只有 a i + k = b k = 1 a_{i+k}=b_k=1 ai+k=bk=1成立,我们才能说这样的字符对存在。
但是怎么求呢?我们现在有了 a i , b i a_i,b_i ai,bi,但是因为 ∑ k = 0 ∣ T ∣ − 1 a i + k b k \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_{i+k}b_{k} k=0∑∣T∣−1ai+kbk中 a , b a,b a,b的下标加起来不是一个常值。如果是一个常值的话,我们就可以把 a i a_i ai数组和 b i b_i bi数组当做两个多项式的系数,然后我们进行多项式的乘法,这时 a i b j a_ib_j aibj自然就是我们两个多项式乘在一起之后 x i + j x^{i+j} xi+j的系数中的一部分。
我们发现,我们要求的这个求和公式的形式等同于 ∑ k = 0 ∣ T ∣ − 1 a i b j \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_ib_j k=0∑∣T∣−1aibj,如果 i + j i+j i+j是定值 C C C,那么我们所求的求和公式的结果就是多项式乘在一起之后 x C x^C xC的系数。
观察我们想求的公式 ∑ k = 0 ∣ T ∣ − 1 a i + k b k \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_{i+k}b_{k} k=0∑∣T∣−1ai+kbk,我们发现,如果 b k b_k bk中的 k k k变成 − k -k −k,哪怕是加一点常数,就完美了。因为这样两个变量 k k k就抵消掉了,剩下的和就是一个定值,就可以通过两个多项式相乘之后的系数求得。
把 b k b_k bk中的 k k k变成 − k -k −k很简单,我们可以直接将 T T T串翻转,这样我们原本的 b k b_k bk就变成了 b ∣ T ∣ − k − 1 b_{\vert T \vert-k-1} b∣T∣−k−1,我们原本要求的求和公式 ∑ k = 0 ∣ T ∣ − 1 a i + k b k \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_{i+k}b_{k} k=0∑∣T∣−1ai+kbk也变成了 ∑ k = 0 ∣ T ∣ − 1 a i + k b ∣ T ∣ − k − 1 \displaystyle\sum\limits_{k=0}^{\vert T\vert - 1} a_{i+k}b_{\vert T\vert-k-1} k=0∑∣T∣−1ai+kb∣T∣−k−1。
这个时候我们 a , b a,b a,b的下标之和就是 ∣ T ∣ + i − 1 \vert T\vert+i-1 ∣T∣+i−1。这里面 ∣ T ∣ \vert T\vert ∣T∣是 T T T的长度,是定值; i i i是当前子问题中 T T T串第一个字符跟 S S S串的哪个字符对齐,在子问题中也是一个定值。于是 ∣ T ∣ \vert T\vert ∣T∣就是一个定值。这样的话,我们就可以利用我们刚刚推出的结论来求解这个求和式了。将两个数组 a , b a,b a,b当做多项式系数后,进行多项式乘法,得到的结果多项式中, x ∣ T ∣ + i − 1 x^{\vert T\vert+i-1} x∣T∣+i−1的系数,就是我们所求的结果。如果这个结果大于 0 0 0,则说明存在这样的字符对 ( c 1 , c 2 ) (c_1,c_2) (c1,c2)。
设 f [ i ] [ c 1 ] [ c 2 ] f[i][c_1][c_2] f[i][c1][c2]为在 T T T串第一个字符跟 S S S串的哪个字符对齐时是否存在字符对 ( c 1 , c 2 ) (c_1,c_2) (c1,c2)。如果存在,其值为 1 1 1,否则为 0 0 0。
所以整体的流程就是:
- 对于字符 c 1 c_1 c1,我们先看 S S S串中哪些位置是 c 1 c_1 c1。设数组 a a a来表示这个信息。如果 a i = 1 a_i=1 ai=1,说明字符串 S S S的第 i i i位是 c 1 c_1 c1;如果 a i = 0 a_i=0 ai=0,说明字符串的第 i i i位不是 c 1 c_1 c1。
- 翻转字符串 T T T。
- 对于字符 c 2 c_2 c2,我们先看 T T T串中哪些位置是 c 2 c_2 c2。设数组 b b b来表示这个信息。如果 b i = 1 b_i=1 bi=1,说明字符串 T T T的第 i i i位是 c 2 c_2 c2;如果 b i = 0 b_i=0 bi=0,说明字符串的第 i i i位不是 c 2 c_2 c2。
- 把得到的 a , b a,b a,b数组当做两个多项式的系数,进行卷积。
- 得到的结果多项式的系数中,如果 0 ≤ ∣ T ∣ + i − 1 < n 0\leq \vert T\vert + i -1 < n 0≤∣T∣+i−1<n,那么只要 x ∣ T ∣ + i − 1 x^{\vert T\vert +i-1} x∣T∣+i−1的系数大于 0 0 0,则可以认为 f [ i ] [ c 1 ] [ c 2 ] = 1 f[i][c_1][c_2]=1 f[i][c1][c2]=1。如果这一项的系数为 0 0 0,则 f [ i ] [ c 1 ] [ c 2 ] = 0 f[i][c_1][c_2]=0 f[i][c1][c2]=0。
这样的话,对于每一对 c 1 , c 2 c_1,c_2 c1,c2,我们都这样操作一遍,就可以得到全部的 f f f数组的信息了,即:我们求得了从 S S S串的第 i i i位作为第一个字符的长度为 ∣ T ∣ \vert T\vert ∣T∣的子串和 T T T串匹配的过程中,字符 c 1 c_1 c1和字符 c 2 c_2 c2是否出现。接下来用这个信息,对于每一个 i i i的位置,看看所有点对的情况,然后用上面说到的方法用并查集合并一下,就得到了每一个位置的答案。
试试分析现在的时间复杂度。多项式乘法采用FFT或者NTT的话,一次DFT/IDFT的时间复杂度是 O ( n log n ) O(n\log n) O(nlogn)。我们一共进行了 30 30 30个两个字母不同的字符对的查询,每一次查询进行了 3 3 3次DFT/IDFT,也就是说光是在多项式乘法上,时间复杂度就是 O ( 30 × 3 n log n ) O(30\times 3 n\log n) O(30×3nlogn)。经过计算发现这个时间复杂度略微有点大。主要原因是 30 × 3 30\times 3 30×3这个常数太大了。
每一个点对都要进行 3 3 3次DFT,这三次 D F T DFT DFT分别做了:
- 将 S S S串的 a a a数组进行DFT
- 将翻转后的 T T T串的 b b b数组进行DFT
- 将得到的结果进行IDFT。
但是,由于我们的字符集是有限大小的,我们每一个字母作为字符对的第一个字母时,都要求一次 a a a数组,进行一次DFT,这是重复操作。 b b b数组也是同理。所以我们可以预处理出 S S S串所有字符的 a a a数组的DFT后的结果,预处理出翻转后 T T T串所有字符的 b b b数组的DFT后的结果。后续求的时候,直接将预处理出的两个数组相乘,然后进行一次IDFT即可。这样,我们进行DFT/IDFT的次数是两个串的 a , b a,b a,b数组DFT预处理 6 + 6 = 12 6+6=12 6+6=12次, 30 30 30个字符对的IDFT 30 30 30次,一共只有 42 42 42次。时间复杂度一下子就砍了一半。
最后求解的时候每一个位置遍历所有字符对 36 36 36个,每一个字符对的操作是常数级(因为字符集很小),所以这个做法整体的时间复杂度可以认为是 O ( 42 n log n + 36 n ) O(42n\log n+36n) O(42nlogn+36n),经过计算,是可以通过本题的。
代码采用NTT。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL mod = (1ll << 47) * 7 * 4451 + 1;
const LL g = 3;
const LL N = 300005;string ss, tt;
LL s[125005], t[125005];
LL f[N][8][8];
LL n, m, c;
LL sa[8][N], ta[8][N];
LL tmp[N];
LL rev[N], fa[8], rk[8];LL mul(LL x, LL y) {return (x * y - (LL)(x / (long double)mod * y + 1e-3) * mod + mod) % mod;
}template<class T> T power(T a, LL b) {T res = 1;for (; b; b >>= 1) {if (b & 1) res = mul(res, a);a = mul(a, a);}return res;
}void change(LL *y, int len) {for (int i = 0; i < len; ++i) {if (i < rev[i]) swap(y[i], y[rev[i]]);}
}void DFT(LL *y, int len, int on) {change(y, len);for (LL h = 2; h <= len; h <<= 1) {LL wn = power(g, (mod - 1) / h);if (on == -1) wn = power(wn, mod - 2); for (int j = 0; j < len; j += h) {LL w = 1ll;for (int k = j; k < j + h / 2; ++k) {LL u = y[k] % mod;LL t = mul(w, y[k + h / 2]);y[k] = (u + t) % mod;y[k + h / 2] = (u - t + mod) % mod;w = mul(w, wn);}}}
}int find(int x) {return ((fa[x] == x) ? x : (fa[x] = find(fa[x])));
}void merge(int i, int j) {int x = find(i), y = find(j);if (rk[x] <= rk[y]) fa[x] = y;else fa[y] = x;if (rk[x] == rk[y] && x != y) ++rk[y];
}void main2() {cin >> ss >> tt;n = ss.length(); m = tt.length();for (int i = 0; i < n; ++i) {s[i] = ss[i] - 'a';sa[s[i]][i] = 1;}for (int i = 0; i < m; ++i) {t[i] = tt[i] - 'a';ta[t[i]][m - i - 1] = 1;}LL len = 1;while (len <= (n + m)) len <<= 1;for (int i = 0; i < len; ++i) {rev[i] = rev[i >> 1] >> 1;if (i & 1) rev[i] |= len >> 1;}for (int i = 0; i < 6; ++i) {DFT(sa[i], len, 1);DFT(ta[i], len, 1);}for (int i = 0; i < 6; ++i) {for (int j = 0; j < 6; ++j) {if (i == j) continue;for (int k = 0; k < len; ++k) {tmp[k] = mul(sa[i][k], ta[j][k]); }DFT(tmp, len, -1);LL inv = power(len, mod - 2);for (int k = 0; k < len; ++k) {tmp[k] = mul(tmp[k], inv);if (k + 1 - m >= 0 and k + 1 - m < n) f[k + 1 - m][i][j] = tmp[k];}}}for (int i = 0; i < n - m + 1; ++i) {for (int j = 0; j < 6; ++j) {fa[j] = j; rk[j] = 1;}int sum = 0;for (int j = 0; j < 6; ++j) {for (int k = 0; k < 6; ++k) {if (j == k or !f[i][j][k]) continue;int fx = find(j), fy = find(k);if (fx != fy) {++sum;merge(fx, fy);}}}cout << sum << ' ';}
}int main() {ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);LL _ = 1;
// cin >> _;while (_--) main2();return 0;
}
相关文章:

【做题笔记】多项式/FFT/NTT
HDU1402 - A * B Problem Plus 题目链接 大数乘法是多项式的基础应用,其原理是将多项式 f ( x ) a 0 a 1 x a 2 x 2 a 3 x 3 ⋯ a n x n f(x)a_0a_1xa_2x^2a_3x^3\cdotsa_nx^n f(x)a0a1xa2x2a3x3⋯anxn中的 x 10 x10 x10,然后让大数的…...
网课搜题 小猿题库多接口微信小程序源码 自带流量主
多接口小猿题库等综合网课搜题微信小程序源码带流量主,网课搜题小程序, 可以开通流量主赚钱 搭建教程1, 微信公众平台注册自己的小程序2, 下载微信开发者工具和小程序的源码3, 上传代码到自己的小程序 源码下载:https://download.csdn.net/download/m0_…...

centos安装conda python3.10
最新版本的conda自带python3.10,直接安装即可。 手动创建一个conda文件夹,进入该文件夹,然后执行以下操作步骤。 1.下载 curl -O https://repo.anaconda.com/miniconda/Miniconda3-latest-Linux-x86_64.sh2.安装 sh Miniconda3-latest-Linux-x86_64.…...

解密京东面试:如何应对Redis缓存穿透?
亲爱的小伙伴们,大家好!欢迎来到小米的微信公众号,今天我们要探讨一个在面试中可能会遇到的热门话题——Redis缓存穿透以及如何解决它。这个话题对于那些渴望进入技术领域的小伙伴们来说,可是必备的哦! 认识Redis缓存…...

#力扣:1. 两数之和@FDDLC
1. 两数之和 - 力扣(LeetCode) 一、Java import java.util.HashMap;class Solution {public int[] twoSum(int[] nums, int target) { //返回数组HashMap<Integer, Integer> map new HashMap<>(); //键:元素值;值&…...

【小沐学Python】各种Web服务器汇总(Python、Node.js、PHP、httpd、Nginx)
文章目录 1、Web服务器2、Python2.1 简介2.2 安装2.3 使用2.3.1 http.server(命令)2.3.2 socketserver2.3.3 flask2.3.4 fastapi 3、NodeJS3.1 简介3.2 安装3.3 使用3.3.1 http-server(命令)3.3.2 http3.3.3 express 4、PHP4.1 简…...
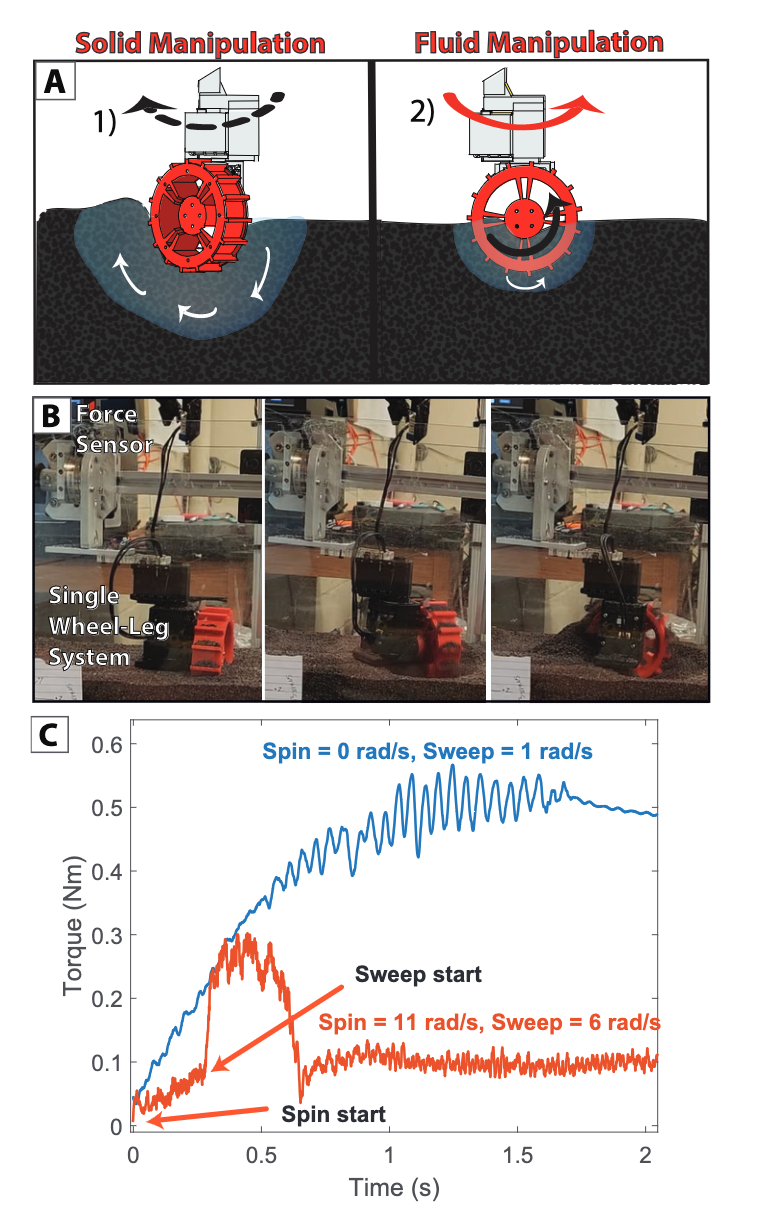
【AI视野·今日Robot 机器人论文速览 第四十六期】Tue, 3 Oct 2023
AI视野今日CS.Robotics 机器人学论文速览 Tue, 3 Oct 2023 Totally 76 papers 👉上期速览✈更多精彩请移步主页 Interesting: 📚Aerial Interaction with Tactile, 无人机与触觉的结合,实现空中交互与相互作用。(from CMU) website&#…...

macOS三种软件安装目录以及环境变量优先级
一、系统自带应用 这些软件(以git为例)位于根目录下的/usr/bin/xxx,又因为系统级环境变量文件/etc/paths已指定了命令查找位置: /usr/local/bin /System/Cryptexes/App/usr/bin /usr/bin /bin /usr/sbin /sbin所以这些自带应用可…...

嵌入式Linux裸机开发(一)基础介绍及汇编LED驱动
系列文章目录 文章目录 系列文章目录前言IMX6ULL介绍主要资料IO表现形式 汇编LED驱动原理图初始化流程时钟设置IO复用设置电气属性设置使用GPIO 编写驱动编译程序编译.o文件地址链接.elf格式转换.bin反汇编(其他) 综合成Makefile完成一步编译烧录程序imx…...
企业微信机器人对接GPT
现在网上大部分微信机器人项目都是基于个人微信实现的,常见的类库都是模拟网页版微信接口。 个人微信作为我们自己日常使用的工具,也用于支付场景,很怕因为违规而被封。这时,可以使用我们的企业微信机器人,利用企业微信…...
【数据结构】排序(1) ——插入排序 希尔排序
目录 一. 直接插入排序 基本思想 代码实现 时间和空间复杂度 稳定性 二. 希尔排序 基本思想 代码实现 时间和空间复杂度 稳定性 一. 直接插入排序 基本思想 把待排序的记录按其关键码值的大小依次插入到一个已经排好序的有序序列中,直到所有的记录插入完为止&…...

Python 列表推导式深入解析
Python 列表推导式深入解析 列表推导式是 Python 中的一种简洁、易读的方式,用于创建列表。它基于一个现有的迭代器(如列表、元组、集合等)来生成新的列表。 基本语法: 列表推导式的基本形式如下: [expression for…...

信息学奥赛一本通-编程启蒙3103:练18.3 组别判断
3103:练18.3 组别判断 时间限制: 1000 ms 内存限制: 65536 KB 提交数: 1963 通过数: 1418 【题目描述】 信息学课上要同学分组做期末报告,分组的方式为依座号顺序,每 3个人一组。如:1, 2, 3 为第一组,4, …...

C++ primer plus--探讨 C++ 新标准
18 探讨 C 新标准 18.1 复习前面介绍过的 C11 功能 (1)C11 扩大了列表初始化的适用范围,使用初始化列表时,可以不加等号。 int x {5}; float y {1.1}; short arr[5] {1, 2, 3, 4, 5}; int* ar new int[4] {1, 2, 3, 4}; vect…...
2023版 STM32实战6 输出比较(PWM)包含F407/F103方式
输出比较简介和特性 -1-只有通用/高级定时器才能输出PWM -2-占空比就是高电平所占的比例 -3-输出比较就是输出不同占空比的信号 工作方式说明 -1-1- PWM工作模式 -1-2- 有效/无效电平 有效电平可以设置为高或低电平,是自己配置的 周期选择与计算 周期重…...
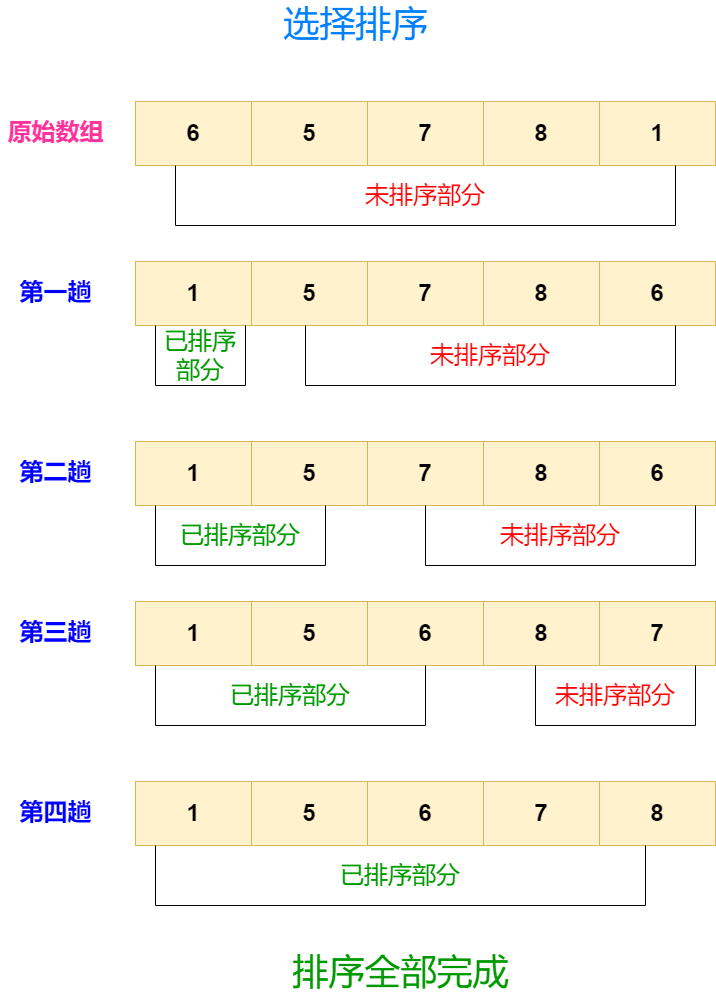
选择排序算法:简单但有效的排序方法
在计算机科学中,排序算法是基础且重要的主题之一。选择排序(Selection Sort)是其中一个简单但非常有用的排序算法。本文将详细介绍选择排序的原理和步骤,并提供Java语言的实现示例。 选择排序的原理 选择排序的核心思想是不断地从…...
安卓教材学习
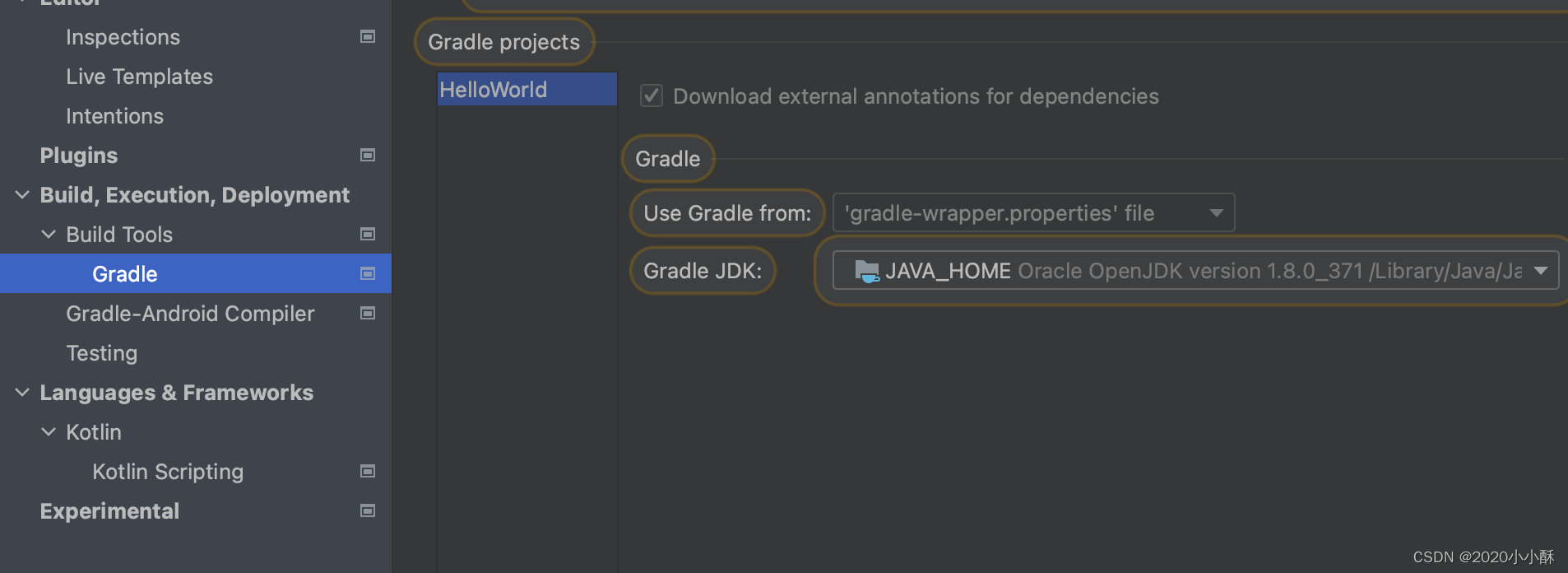
文章目录 教材学习第一行代码 Android 第3版环境配置gradle配置下载包出现问题 教材学习 摘要:选了几本教材《第一行代码 Android 第3版》,记录一下跑案例遇到的问题,和总结一些内容。 第一行代码 Android 第3版 环境配置 gradle配置 gradl…...
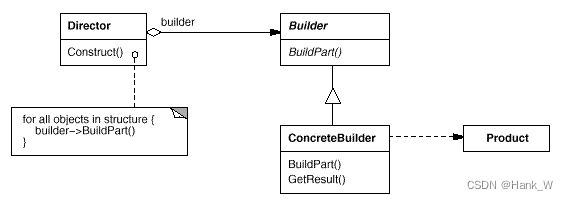
C++设计模式-生成器(Builder)
目录 C设计模式-生成器(Builder) 一、意图 二、适用性 三、结构 四、参与者 五、代码 C设计模式-生成器(Builder) 一、意图 将一个复杂对象的构建与它的表示分离,使得同样的构建过程可以创建不同的表示。 二、…...

CTFHUB - SSRF
目录 SSRF漏洞 攻击对象 攻击形式 产生漏洞的函数 file_get_contents() fsockopen() curl_exec() 提高危害 利用的伪协议 file dict gopher 内网访问 伪协议读取文件 端口扫描 POST请求 总结 上传文件 总结 FastCGI协议 CGI和FastCGI的区别 FastCGI协议 …...
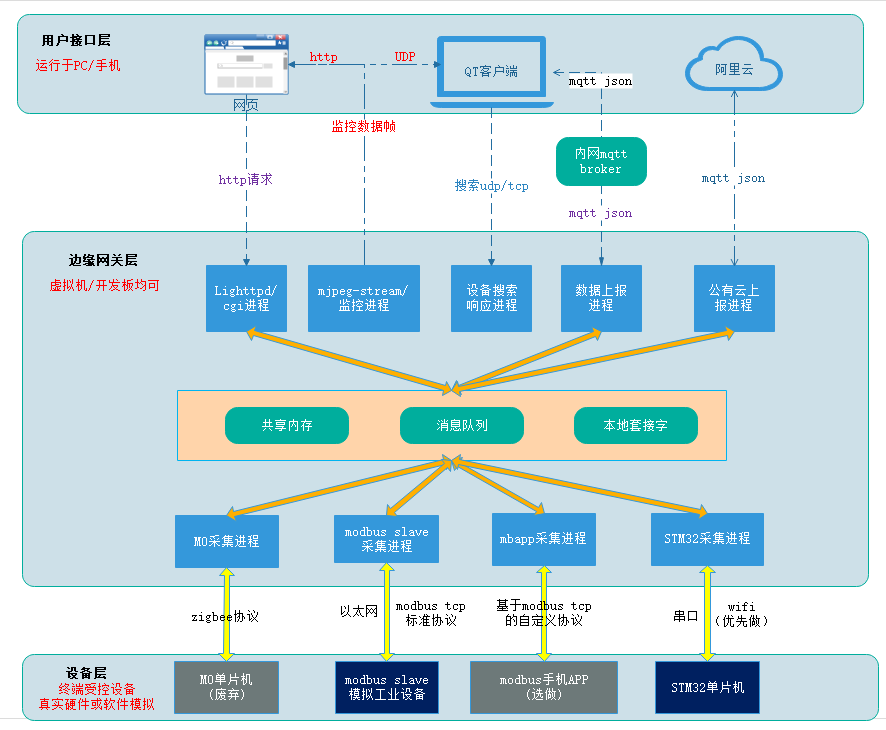
边缘计算网关
一、项目整体框架图 二、项目整体描述 边缘计算网关项目主要实现了智能家居场景和工业物联网场景下设备的数据采集和控制。 整个项目分为三大层:用户接口层、网关层、设备层。 其中用户层通过QT客户端、WEB界面及阿里云提供数据展示和用户接口。 网关使用虚拟机代替…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里
写一个shell脚本,把局域网内,把能ping通的IP和不能ping通的IP分类,并保存到两个文本文件里 脚本1 #!/bin/bash #定义变量 ip10.1.1 #循环去ping主机的IP for ((i1;i<10;i)) doping -c1 $ip.$i &>/dev/null[ $? -eq 0 ] &&am…...
