选择排序算法:简单但有效的排序方法
在计算机科学中,排序算法是基础且重要的主题之一。选择排序(Selection Sort)是其中一个简单但非常有用的排序算法。本文将详细介绍选择排序的原理和步骤,并提供Java语言的实现示例。

选择排序的原理
选择排序的核心思想是不断地从待排序的元素中选择最小的元素,然后将其放置在已排序部分的末尾。它的过程类似于人们在扑克牌中不断选择最小的牌并将其放置在手中的已排序牌的最后一张。这个过程重复进行,直到所有牌都被排序完毕。
选择排序的步骤
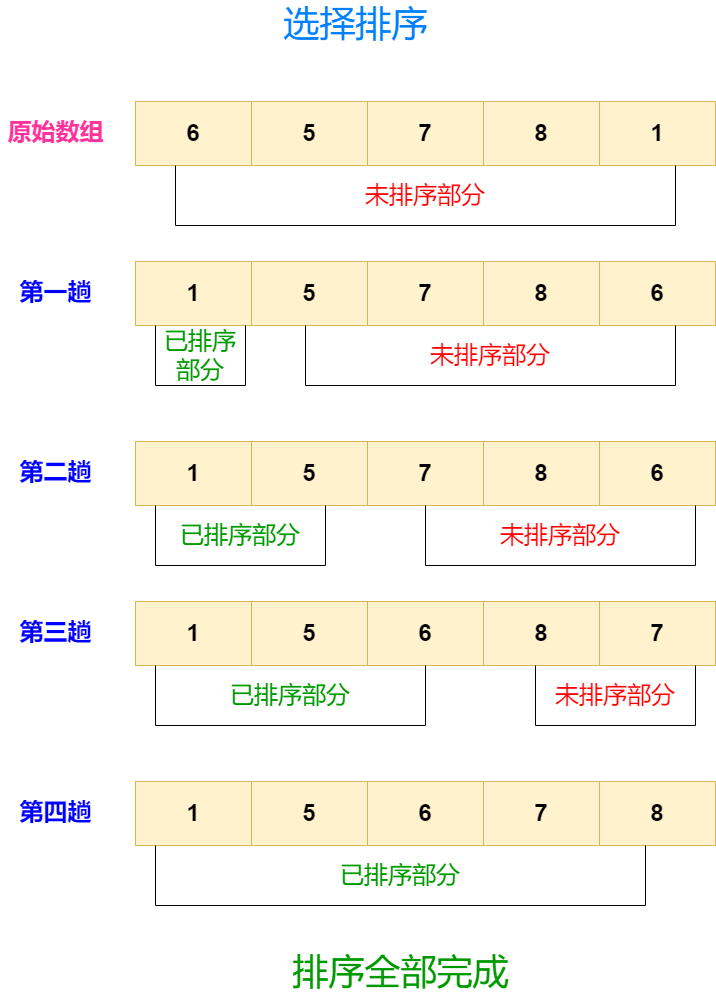
选择排序的步骤可以简单概括为以下几个阶段:
-
初始状态: 将整个数组视为未排序的部分。
-
第一次选择: 从未排序部分选择最小的元素,并将其与未排序部分的第一个元素交换位置。此时,第一个元素被视为已排序的一部分,而其余部分是未排序的。
-
第二次选择: 从剩余未排序部分选择最小的元素,并将其与未排序部分的第一个元素交换位置。现在,前两个元素被视为已排序的一部分,而其余部分是未排序的。
-
重复: 重复上述选择和交换的过程,每次选择并交换一个最小的元素,直到整个数组变为已排序状态。
-
完成: 当算法完成时,整个数组都已排序。
Java代码选择排序
以下是使用Java语言实现选择排序算法的示例代码:
public class Test {public static void main(String[] args) {int[] arr = new int[]{5,2,4,6,7,1,3};selectionSort(arr);}public static void selectionSort(int[] arr){System.out.println("原始数组:"+ Arrays.toString(arr));//获取数组长度int len = arr.length;//循环len-1次,进行数组排序,没排序完一趟,则从下标为i的元素及之后的元素为未排序的部分for(int i = 0; i< len-1; i++){//默认未排序的部分的第一个元素为最小元素下标int minIndex = i;//循环未排序的部分的数组,找出最小6元素的下标for(int j = i+1; j < len; j++){if(arr[j] < arr[minIndex]){minIndex = j;}}//将最小元素与未排序的部分的数组的第一个元素交换int temp = arr[i];arr[i] = arr[minIndex];arr[minIndex] = temp;// 打印每趟排序完成后的数组状态,以便查看排序进度System.out.println("第"+(i+1)+"趟排序完成的数组:"+ Arrays.toString(arr));}System.out.println("排序完成的数组:"+ Arrays.toString(arr));}
}打印结果为:
原始数组:[5, 2, 4, 6, 7, 1, 3]
第1趟排序完成的数组:[1, 2, 4, 6, 7, 5, 3]
第2趟排序完成的数组:[1, 2, 4, 6, 7, 5, 3]
第3趟排序完成的数组:[1, 2, 3, 6, 7, 5, 4]
第4趟排序完成的数组:[1, 2, 3, 4, 7, 5, 6]
第5趟排序完成的数组:[1, 2, 3, 4, 5, 7, 6]
第6趟排序完成的数组:[1, 2, 3, 4, 5, 6, 7]
排序完成的数组:[1, 2, 3, 4, 5, 6, 7]
以上代码演示了如何使用选择排序对一个整数数组进行排序。选择排序算法虽然不如一些高级排序算法快速,但它易于理解和实现,对于小型数据集或接近排序状态的数据集可能是一个合理的选择。
总结
选择排序虽然不是最高效的排序算法,但它是一个简单而直观的例子,有助于理解排序算法的基本原理。希望本文的解释和示例有助于您更好地理解选择排序,并在需要时应用它来解决排序问题。
相关文章:

选择排序算法:简单但有效的排序方法
在计算机科学中,排序算法是基础且重要的主题之一。选择排序(Selection Sort)是其中一个简单但非常有用的排序算法。本文将详细介绍选择排序的原理和步骤,并提供Java语言的实现示例。 选择排序的原理 选择排序的核心思想是不断地从…...
安卓教材学习
文章目录 教材学习第一行代码 Android 第3版环境配置gradle配置下载包出现问题 教材学习 摘要:选了几本教材《第一行代码 Android 第3版》,记录一下跑案例遇到的问题,和总结一些内容。 第一行代码 Android 第3版 环境配置 gradle配置 gradl…...
C++设计模式-生成器(Builder)
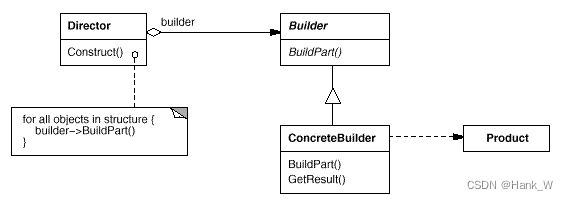
目录 C设计模式-生成器(Builder) 一、意图 二、适用性 三、结构 四、参与者 五、代码 C设计模式-生成器(Builder) 一、意图 将一个复杂对象的构建与它的表示分离,使得同样的构建过程可以创建不同的表示。 二、…...

CTFHUB - SSRF
目录 SSRF漏洞 攻击对象 攻击形式 产生漏洞的函数 file_get_contents() fsockopen() curl_exec() 提高危害 利用的伪协议 file dict gopher 内网访问 伪协议读取文件 端口扫描 POST请求 总结 上传文件 总结 FastCGI协议 CGI和FastCGI的区别 FastCGI协议 …...
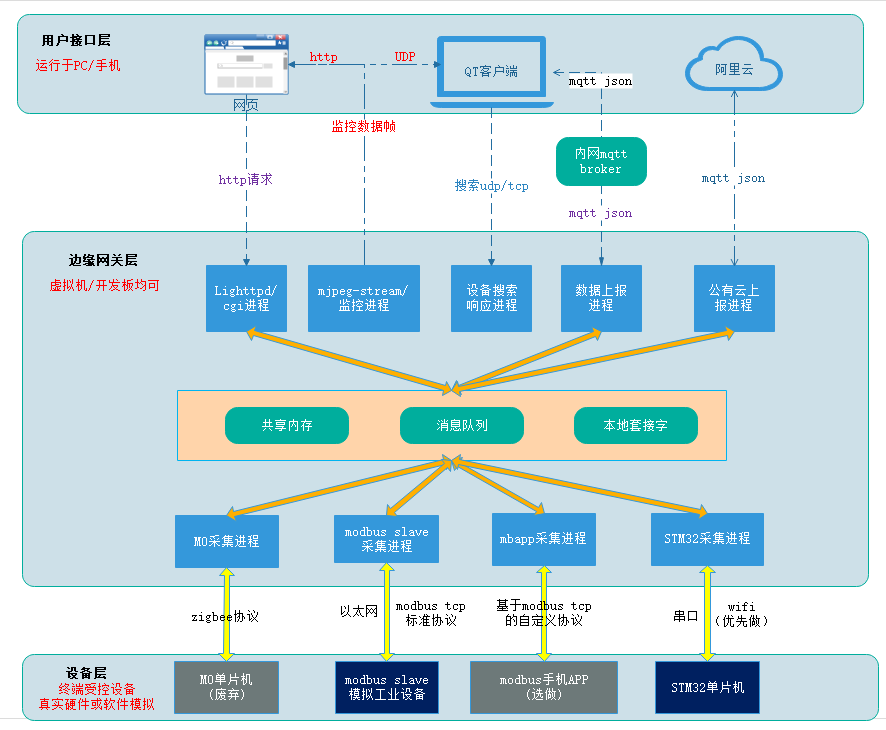
边缘计算网关
一、项目整体框架图 二、项目整体描述 边缘计算网关项目主要实现了智能家居场景和工业物联网场景下设备的数据采集和控制。 整个项目分为三大层:用户接口层、网关层、设备层。 其中用户层通过QT客户端、WEB界面及阿里云提供数据展示和用户接口。 网关使用虚拟机代替…...
1800_vim的宏录制功能尝试
全部学习信息汇总: GreyZhang/editors_skills: Summary for some common editor skills I used. (github.com) 最近5年多来,我emacs的编辑器用的还是比较多的。我的配置基本上是一个spacemacs,然后根据自己的需求增加了一丁点儿的其他配置。而…...

Ultra-Fast-Lane-Detection-v2 {后处理优化}//参考
采用三次多项式拟合生成的anchor特征点,在给定的polyfit_draw函数中,degree参数代表了拟合多项式的度数。 具体来说,当我们使用np.polyfit函数进行数据点的多项式拟合时,我们需要指定一个度数。这个度数决定了多项式的复杂度。例…...

【面试题精讲】Java静态方法和实例方法有何不同?
★ 有的时候博客内容会有变动,首发博客是最新的,其他博客地址可能会未同步,认准https://blog.zysicyj.top ” 首发博客地址[1] 面试题手册[2] 系列文章地址[3] Java 中的静态方法和实例方法在使用和行为上有一些不同之处。 调用方式不同: 静…...
【数据结构】布隆过滤器
布隆过滤器的提出 在注册账号设置昵称的时候,为了保证每个用户昵称的唯一性,系统必须检测你输入的昵称是否被使用过,这本质就是一个key的模型,我们只需要判断这个昵称被用过,还是没被用过。 方法一:用红黑…...

linux基础4---内存
1、什么是内存泄漏,怎么解决内存泄漏? 在嵌入式Linux中,内存泄漏是指由于疏忽或错误,导致一些对象或资源无法被垃圾回收器回收,从而导致内存占用不断增加,最终导致设备性能下降。内存泄漏对程序的影响很大,可能会导致应用程序变慢、崩溃或者消耗大量的内存,最终导致设…...

图论---拓扑排序
概念 一个有向图,如果图中有入度为 0 的点,就把这个点删掉,同时也删掉这个点所连的边。一直进行上面的处理,如果所有点都能被删掉,则这个图可以进行拓扑排序。拓扑排序是对DAG(有向无环图)上的节…...
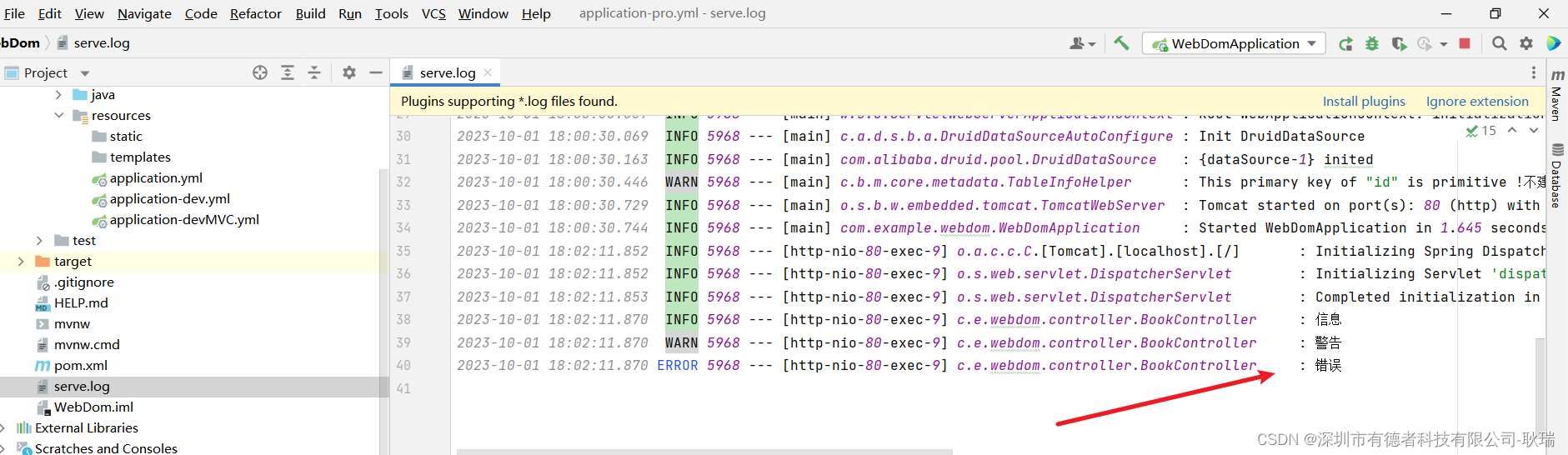
java Spring Boot 将日志写入文件中记录
我们之前的一套操作来讲 日志都是在控制台上的 但 如果你的项目在正式环境上跑 运维人员突然告诉你说日志报错了,但你日志只在控制台上,那公司项目如果访问量很大 那你是很难在控制台上找到某一条日志的 这时 我们就可以用文件把它记下来 我们打开项目 …...
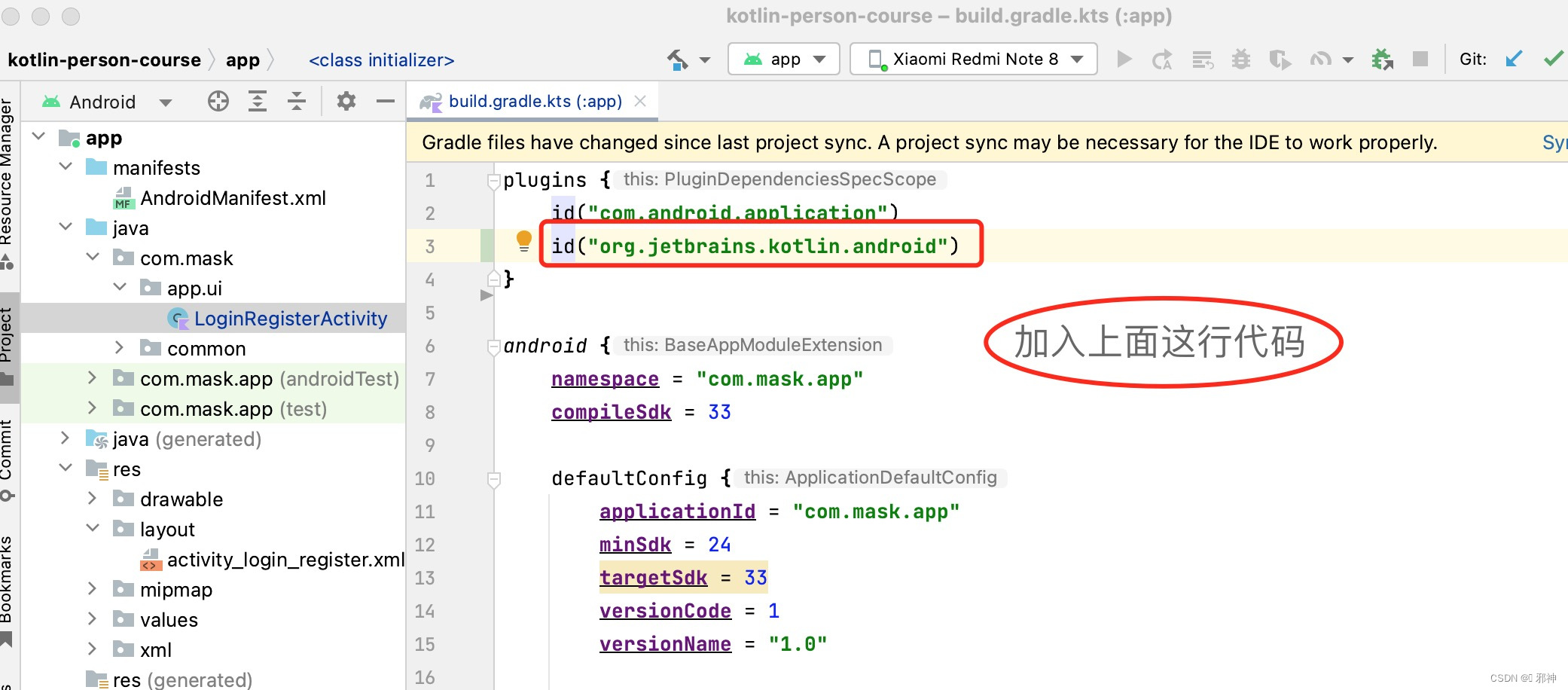
Android 开发错误集合
🔥 开发错误集合一 🔥 Caused by: java.lang.ClassNotFoundException: Didnt find class "com.mask.app.ui.LoginRegisterActivity" on path: DexPathList[[zip file "/data/app/~~NMvHVhj8V6-HwGbh2amXDA/com.mask.app-PWbg4xIlETQ3eVY…...

VSCode个人设置习惯
账号登陆同步 点击左下角齿轮或者用户头像–>Turn on Settings Sync–>全选–>Sign in &Turn on。 可以同步配置、快捷键、插件、用户代码片段、UI状态 Windows下将powershell改为cmd 在vscode打开集成终端,点击右上角加号右边的下拉菜单,…...
 322. 零钱兑换 279.完全平方数)
代码随想录训练营二刷第四十七天 | 70. 爬楼梯 (进阶) 322. 零钱兑换 279.完全平方数
代码随想录训练营二刷第四十七天 | 70. 爬楼梯 (进阶) 322. 零钱兑换 279.完全平方数 一、70. 爬楼梯 (进阶) 题目链接:https://leetcode.cn/problems/climbing-stairs/ 思路:物品是楼梯1和2,…...
beego-简单项目写法--后续放到git上
Beego案例-新闻发布系统 1.注册 后台代码和昨天案例代码一致。,所以这里面只写一个注册的业务流程图。 **业务流程图 ** 2.登陆 业务流程图 登陆和注册业务和我们昨天登陆和注册基本一样,所以就不再重复写这个代码 但是我们遇到的问题是如何做代码的迁移&…...
【算法|动态规划No.9】leetcodeLCR 091. 粉刷房子
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【手撕算法系列专栏】【LeetCode】 🍔本专栏旨在提高自己算法能力的同时,记录一下自己的学习过程,希望…...
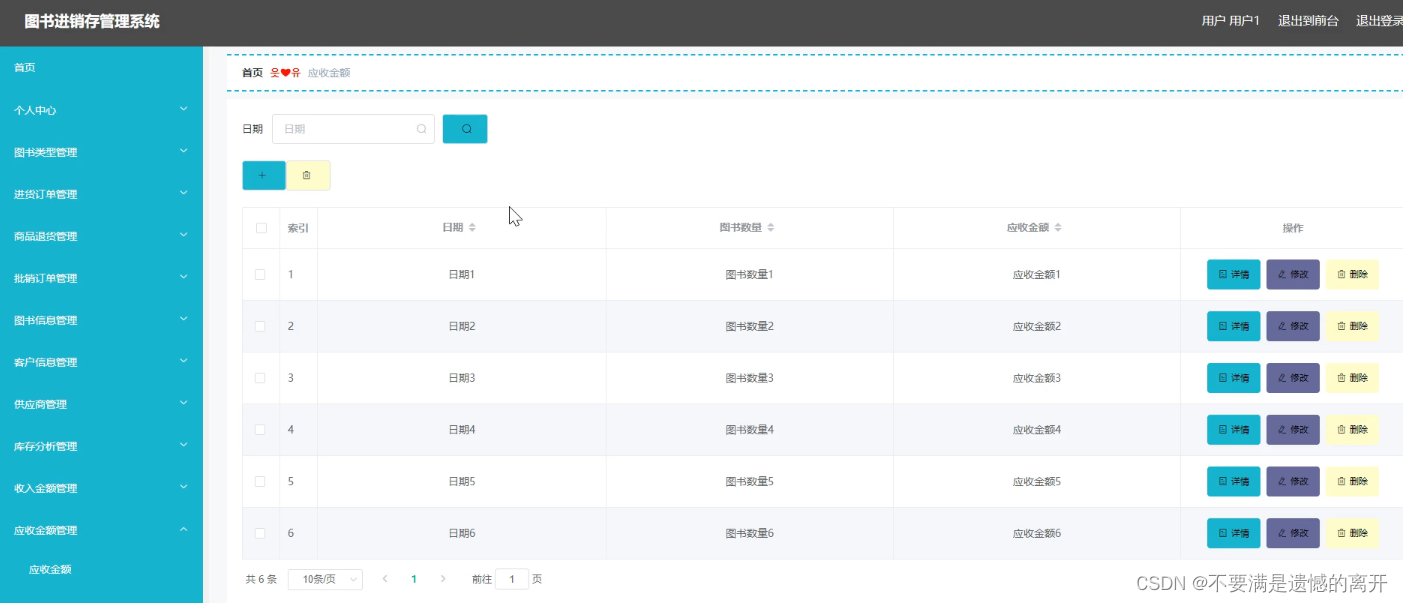
基于SpringBoot的图书进销存管理系统
目录 前言 一、技术栈 二、系统功能介绍 用户信息管理 图书类型管理 商品退货管理 客户信息管理 图书添加 客户添加 应收金额 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实…...

回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测
回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测 目录 回归预测 | MATLAB实现PSO-SVR粒子群优化支持向量机回归多输入单输出预测预测效果基本介绍模型描述程序设计预测效果 <...

vue3使用v-model控制子组件进行双向数据绑定
vue2写法: 中父组件调用子组件: <child :isShow.sync"isShow" v-show"isShow"/> 子组件想要消失, 在子组件写: this.$emit("update:isShow",false); 具体代码就不粘贴了 vue3写法: 父组件核心代码: v-model:a"xxx" 子组…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
