[C国演义] 第十三章
第十三章
- 三数之和
- 四数之和
三数之和
力扣链接

根据题目要求:
- 返回的数对应的下标各不相同
- 三个数之和等于0
- 不可包含重复的三元组 – – 即
顺序是不做要求的
如: [-1 0 1] 和 [0, 1, -1] 是同一个三元组 - 输出答案顺序不做要求
暴力解法: 排序 + 3个for循环 + 去重 — — N^3, 肯定超时
优化: 排序 + 双指针 + 去重 — — N^2
优化的具体思路:
固定一个数, 记作a; 在剩余的空间里面找和为 -a的两个数(由于是排好序的, 所以使用双指针)
去重有两种方法:
1.set去重
2 在循环内部缩小空间 — — 非常值得我们去尝试
- set去重
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {// 排序sort(nums.begin(), nums.end());// 记录结果vector<vector<int>> res; // 固定一个数 + 双指针int n = nums.size();for(int i = 0; i < n; i++) // 固定一个数{// 双指针优化int left = i+1, right = n-1;int targt = -nums[i];while(left < right){int sum = nums[left] + nums[right];if(sum < targt){left++;}else if(sum > targt){right--;}else{res.push_back({nums[i], nums[left], nums[right]});left++;right--;}}}// 去重set<vector<int>> result(res.begin(), res.end());res.clear();for(auto e : result){res.push_back(e);}return res;}
};
上面的运行结果太慢了, 我们尝试一下 缩小空间去重👇👇👇
- 缩小空间去重
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {// 排序sort(nums.begin(), nums.end());// 记录结果vector<vector<int>> res; // 固定一个数 + 双指针int n = nums.size();for(int i = 0; i < n;) // 固定一个数{// 双指针优化int left = i+1, right = n-1;int targt = -nums[i];while(left < right){int sum = nums[left] + nums[right];if(sum < targt){left++;}else if(sum > targt){right--;}else{res.push_back({nums[i], nums[left], nums[right]});left++;right--;// 去重left 和 rightwhile(left < right && nums[left] == nums[left-1]) left++;while(right > left && nums[right] == nums[right+1]) right--;}}// 去重ii++;while(i < n && nums[i] == nums[i-1]) i++;}return res;}
};




四数之和
力扣链接

这一题就跟上面的题目相似, 思路也很相似: 排序 + 固定两个数, 双指针优化 + 去重. 当然, 我们这里的去重逻辑也是 缩小空间去重
class Solution {
public:vector<vector<int>> fourSum(vector<int>& nums, int target) {sort(nums.begin(), nums.end());vector<vector<int>> res;int n = nums.size();// 选定一个数, 内部用三数之和for(int i = 0; i < n;){// 选定一个数, 内部使用双指针优化for(int j = i+1; j < n;){int left = j+1, right = n-1;long int tar = target - (long int)(nums[i]+nums[j]);while(left < right){long int cur = nums[left] + nums[right];if(cur < tar) left++;else if(cur > tar) right--;else{res.push_back({nums[i], nums[j], nums[left], nums[right]});left++, right--;// 去重left 和 rightwhile(left < right && nums[left] == nums[left-1]) left++;while(right > left && nums[right] == nums[right+1]) right--;}}// j的去重j++;while(j < n && nums[j] == nums[j-1]) j++;}// i的去重i++;while(i < n && nums[i] == nums[i-1]) i++;}return res;}
};
号令风霆迅,天声动北陬。
长驱渡河洛,直捣向燕幽。
马蹀阏氏血,旗袅可汗头。
归来报明主,恢复旧神州。 — — [宋] 岳飞 <送紫岩张先生北伐>
相关文章:

[C国演义] 第十三章
第十三章 三数之和四数之和 三数之和 力扣链接 根据题目要求: 返回的数对应的下标各不相同三个数之和等于0不可包含重复的三元组 – – 即顺序是不做要求的 如: [-1 0 1] 和 [0, 1, -1] 是同一个三元组输出答案顺序不做要求 暴力解法: 排序 3个for循环 去重 — — N^3, …...
<二>Qt斗地主游戏开发:过场动画的实现
1. 过场动画效果 2. 思路分析 过场动画较为简单,只有一个进度条在进行滚动,因此实现起来不需要动画相关处理,仅需要图片和定时器设定,让进度条动起来即可。我们可以创建一个对话框,设定背景图片以及对话框透明无边框&a…...
)
链式法则(Chain Rule)
定义 链式法则(Chain Rule)是概率论和统计学中的一个基本原理,用于计算联合概率分布或条件概率分布的乘积。它可以用于分解一个复杂的概率分布为多个较简单的条件概率分布的乘积,从而简化概率分析问题。 链式法则有两种常见的形…...

AUTOSAR COM模块框架梳理
框架: COM的功能主要就是两个: 把IPDU内的signal提取出来提供给SWC使用,把SWC发送的signal拷贝到IPDU buffer内 所以,COM的关键字是 signal, signal group, IPDU, IPDU group Signal group 是为了保证 Complex Data Types 的数…...

详细介绍区块链之挖矿
对不起,大家,这篇文章对作者来说实在是太有意义和含金量了,作者想把它设置为关注博主才能见全文,请大家理解!如果觉得还是看不懂,抱歉耽误大家的时间,就请取消关注!!&…...
)
华为OD机试真题-路灯照明问题(Java/C++/Go/Python)
【华为OD机试真题】路灯照明问题(Java/C++/Go/Python) 题目描述 在一条笔直的公路上安装了N个路灯,从位置0开始安装,路灯之间间距固定为100米。 每个路灯都有自己的照明半径,请计算第一个路灯和最后一个路灯之间,无法照明的区间的长度和。 输入描述 第一行为一个数N…...

嵌入式技术面试基本规则
潜规则1:面试的本质不是考试,而是告诉面试官你会做什么 经验不够的小伙伴特别容易犯的一个错误,不清楚面试官到底想问什么,其实整个面试中面试官并没有想难倒你的意思,只是想通过提问的方式来知道你会什么。 比如stm…...
osg实现自定义插件读取自定义格式的模型文件到场景
目录 1. 前言 2. 预备知识 3. 工具、原料 4. 代码实现 1. 前言 osg提供了很多插件来读取模型文件到场景中,这些插件支持大约70种格式类型的文件,但现实中的文件是各式各样,osg不可能囊括所有类型文件,当osg不支持某种类型格式…...

redis进阶
redis.conf 启动的时候就通过配置文件来启动的! # 这个不是配置的,就是在这儿说明一下 # 当配置中需要配置内存大小时,可以使用 1k, 5GB, 4M 等类似的格式,其转换方式如下(不区分大小写) # # 1k > 1000 bytes # 1kb > 102…...
(一)正点原子STM32MP135移植——准备
一、简述 使用板卡:正点原子的ATK-DLMP135 V1.2 从i.mx6ull学习完过来,想继续学习一下移植uboot和内核的,但是原子官方没有MP135的移植教程,STM32MP157的移植教程用的又是老版本的代码,ST官方更新后的代码不兼容老版本…...

Kotlin的关键字 lateinit 和 lazy
序、完善一下曾经的草稿。 Kotlin通常要求我们在定义属性后立即对起进行初始化,当我们不知道理想的初始值时,这样做似乎很奇怪,尤其是在生命周期驱动android属性的情况下。 lateinit 简介 lateinit,Kotlin提供的一个可以延迟初…...
阿里云服务器ECS详细介绍_云主机_服务器托管_弹性计算
阿里云服务器ECS英文全程Elastic Compute Service,云服务器ECS是一种安全可靠、弹性可伸缩的云计算服务,阿里云提供多种云服务器ECS实例规格,如经济型e实例、通用算力型u1、ECS计算型c7、通用型g7、GPU实例等,阿里云服务器网分享阿…...

12、建立健全人员培训体系
9、大小屏分离与精细化审核 10、质量审核的设立与合并 11、视频分类建议 内容仓为公司其他部门输送了许多人才,既包括有潜力的主管,也有表现突出或者具备某些特殊能力的员工,从内容仓走出的同事,有些已经成为公司重要业务某个方…...
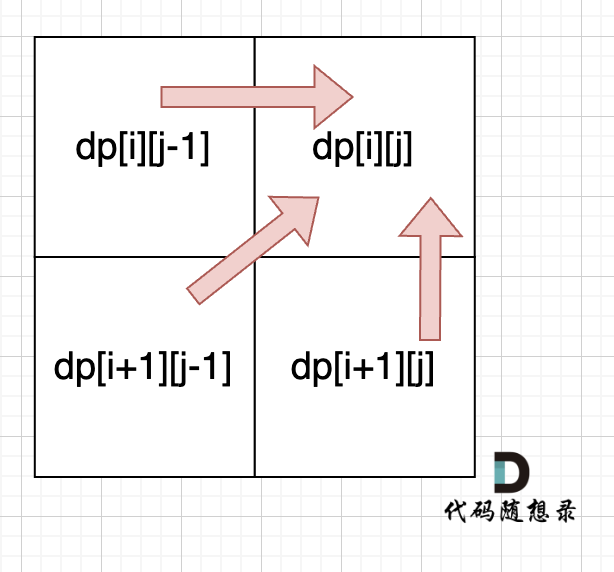
代码随想录算法训练营第五十九天 | 647. 回文子串 516.最长回文子序列
1. 回文子串 647. 回文子串 - 力扣(LeetCode) 一个子串左右两个元素相等,并且中间对称,才是回文子串 即 ij 时,[i1: j-1]对称 dp[i][j]: [i:j] 是否是回文字串 当 子串长度大于2 由 dp[i1][j-1] 推出…...

React Redux
redux是什么 Redux是一个模式和库,用于管理和更新应用程序状态,使用称为“action”的事件。它是需要在整个应用程序中使用的状态的集中存储,规则确保状态只能以可预测的方式更新。 Redux主要有三个功能: 获取当前状态更新状态监…...

StreamingLLM - 处理无限长度的输入
文章目录 关于 StreamingLLM使用关于 StreamingLLM Efficient Streaming Language Models with Attention Sinks GitHub : https://github.com/mit-han-lab/streaming-llm论文:https://arxiv.org/abs/2309.17453在流媒体应用程序(如多轮对话)中 部署大型语言模型(LLM)是迫…...

[Linux 命令] nm 详解
1. nm 命令: 显示关于指定 File 中符号的信息,文件可以是对象文件、可执行文件或对象文件库。如果文件没有包含符号信息,nm 命令报告该情况,但不把它解释为出错条件。 nm 命令缺省情况下报告十进制符号表示法下的数字值。 2. 命…...

好文学作品的鉴赏标准
好文学作品的鉴赏标准 2023年诺贝尔文学奖颁给了挪威剧作家约恩福瑟。由于之前的博彩公司给中国作家残雪开出了最高的赔率,以及诺贝尔官方推特在揭晓奖项前发布了一张泰戈尔99年前访华的老照片,残雪的获奖氛围在国内各类媒体的渲染下被拉至极高。当奖项…...

智慧公厕:将科技融入日常生活的创新之举
智慧公厕是当今社会中一项备受关注的创新项目。通过将科技融入公厕设计和管理中,这些公厕不仅能够提供更便利、更卫生的使用体验,还能够极大地提升城市形象和居民生活质量。本文将以智慧公厕领先厂家广州中期科技有限公司,大量的精品案例项目…...
ROS(0)命令及学习资源汇总
ROS安装命令 参考:Ubuntu20.04.4安装ROS Noetic详细教程 - 知乎 安装C和Python3 sudo apt-get install g sudo apt-get install python3 ROS运行小海龟仿真器 roscore确定ROS是否运行成功rosrun turtlesim turtlesim_node运行小海龟仿真器rosrun turtlesim turtle_…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
