【锁的区别】C++线程库和POSIX线程库锁的区别
C++线程库和POSIX线程库锁的区别
- C++线程库
- 代码段的互斥:mutex、recursive_mutex、timed_mutex、recursive_timed_mutex
- 互斥量mutex:直接进行lock()或者unlock()
- 递归互斥锁recursive_mutex:可以多次加锁,意味着加几次锁就需要解几次锁
- 定时互斥锁timed_mutex:可以定时加锁,规定什么时间让临界区代码实现互斥访问
- 递归定时互斥锁recursive_timed_mutex:在规定加锁时间的同时,还能实现递归的多次加锁要求
- lock_guard:RAII的方式封装了锁
- unique_lock:RAII方式+加锁/解锁
- 变量的原子性操作:atomic
- POSIX线程库
- 互斥锁:pthread_mutex
- 自旋锁:pthread_spin
- 读写锁:pthread_rwlock
C++线程库
C++线程库中提供了多种类型的原子性操作,主要分为变量的原子性操作和代码段的互斥加锁
代码段的互斥:mutex、recursive_mutex、timed_mutex、recursive_timed_mutex
如果一段代码是在多线程编程下执行的,那么必然要涉及到线程安全的问题,需要对该代码段进行加锁保护
#include <iostream>
#include <mutex>
#include <thread>
#include <vector>std::mutex g_mutex;
int g_count = 0;void Counter() {g_mutex.lock();int i = ++g_count;std::cout << "count: " << i << std::endl;// 前面代码如有异常,unlock 就调不到了。g_mutex.unlock();
}int main() {const std::size_t SIZE = 4;// 创建一组线程。std::vector<std::thread> v;v.reserve(SIZE);for (std::size_t i = 0; i < SIZE; ++i) {v.emplace_back(&Counter);}// 等待所有线程结束。for (std::thread& t : v) {t.join();}return 0;
}互斥量mutex:直接进行lock()或者unlock()
上述例子中,使用了mutex这个锁,也就是c++中提出的锁,但是这样的方式导致一个线程执行g_count时,其他线程在进行阻塞等待,是有其自己的缺陷的
递归互斥锁recursive_mutex:可以多次加锁,意味着加几次锁就需要解几次锁
定时互斥锁timed_mutex:可以定时加锁,规定什么时间让临界区代码实现互斥访问
递归定时互斥锁recursive_timed_mutex:在规定加锁时间的同时,还能实现递归的多次加锁要求
lock_guard:RAII的方式封装了锁
使用了RAII的思想,让类对象1去管理锁资源,在创建对象的时候加锁,析构对象的时候解锁,以此来预防死锁
unique_lock:RAII方式+加锁/解锁
除了使用RAII的思想之外,还提供了加锁解锁修改锁的功能,比lock_guard增加了一些对锁的操作
变量的原子性操作:atomic
int a
这个变量在整个多线程编程中如果是一个全局变量(局部变量也可以),那么当多个线程需要对其进行修改操作时,必然涉及到线程安全的问题,需要对这个变量加锁保护,但是使用上述的mutex类型会显得大炮打苍蝇,有点兴师动众了,同时如果使用mutex加锁的方式来实现互斥,会让其他线程处于阻塞等锁的状态,会影响程序的效率
c++11中提供了一系列原子操作
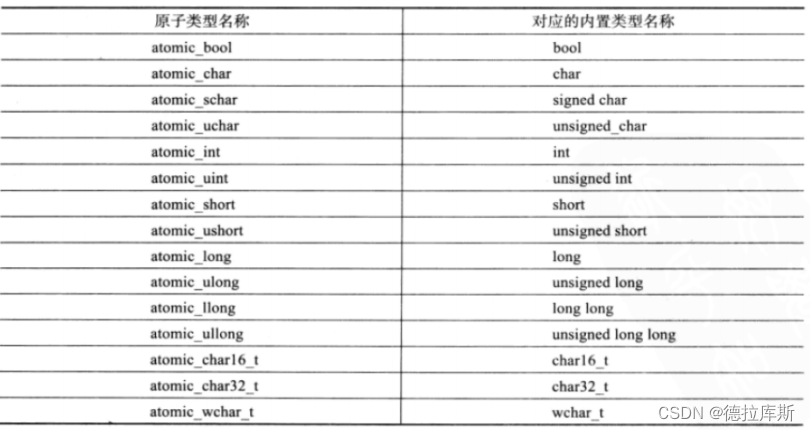
#include <iostream>
using namespace std;
#include <thread>
//需要包含对应的头文件
#include <atomic>
atomic_long sum{ 0 };
void fun(size_t num)
{for (size_t i = 0; i < num; ++i)sum ++; // 原子操作
}
int main()
{cout << "Before joining, sum = " << sum << std::endl;thread t1(fun, 1000000);thread t2(fun, 1000000);t1.join();t2.join();cout << "After joining, sum = " << sum << std::endl;return 0;
}
将普通变量修改为原子类型的变量,这样就无需进行加锁解锁操作了,会使代码的运行效率更高,线程自己就能够对这些原子类型的变量实现互斥访问了
POSIX线程库
互斥锁:pthread_mutex
有线程尝试加互斥锁时,如果没有加到锁,该线程会挂起并且切换,只有当其他线程将该互斥锁释放之后,该线程才会被唤醒继续加锁。
和C++中的mutex相似,可以对临界区代码进行加锁保护,但是需要对该互斥锁初始化,并且需要进行销毁
pthread_mutex_init()//初始化
pthread_mutex_lock()//加锁
pthread_mutex_unlock()//解锁
pthread_mutex_destroy()//销毁
自旋锁:pthread_spin
与互斥锁相比,它的效率更高,但是也更占CPU资源。
当有线程尝试加自旋锁时,如果该线程没有加到锁,那么会持续加锁,直到拿到锁为止,线程不会挂起也不会切换,因此加锁效率高,但也更加占用CPU资源
读写锁:pthread_rwlock
当存在这样的场景时:对数据的修改操作少,有大量的读数据操作,在这样的情况下对临界资源进行加锁会导致程序效率低下,那么就需要有一个读不加锁,而只有在写数据的时候才进行加锁来提高程序的效率,读写锁就是这样一个锁
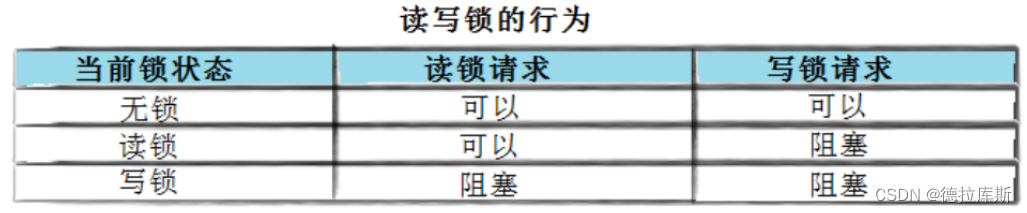
读共享,写独占,读锁优先级高
相关文章:

【锁的区别】C++线程库和POSIX线程库锁的区别
C线程库和POSIX线程库锁的区别 C线程库代码段的互斥:mutex、recursive_mutex、timed_mutex、recursive_timed_mutex互斥量mutex:直接进行lock()或者unlock()递归互斥锁recursive_mutex:可以多次加锁,意味着加几次锁就需要解几次锁…...

网络层·IP协议
承接前文TCP协议-CSDN博客 简介 协议头格式 网段划分(重要) 划分方法 IP地址的数量限制(背景介绍) 私有IP地址和公网IP地址(提出解决思路) NAT技术(解决方法) 路由 网络层 在复杂的网络环境中确定一个合适的路径 IP协议 主机: 配有IP地址, 可以认为就是你的电脑; 路由器:…...
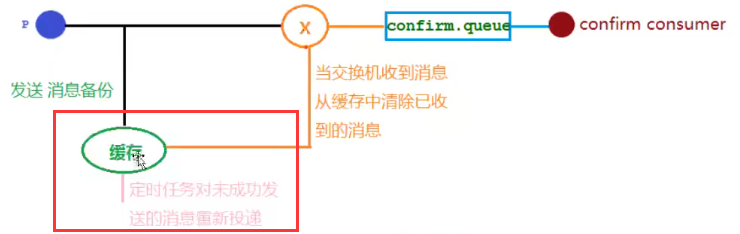
RabbitMQ学习笔记(下):延迟队列,发布确认高级,备份交换机
十、延迟队列 延迟队列 概念: 延迟队列使用场景: 流程图: 延迟队列整合Springboot 导入依赖: <dependencies><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot…...

Python 无废话-基础知识面向对象编程详解
类定义 如何理解万物皆对象? 生活中一些事物,动物(可爱的小狗、调皮的小猫)、交通工具(比亚迪U8汽车、飞机)、人(学生、教师)…… 这些对象都有着独特或共性的属性和方法来描述其…...
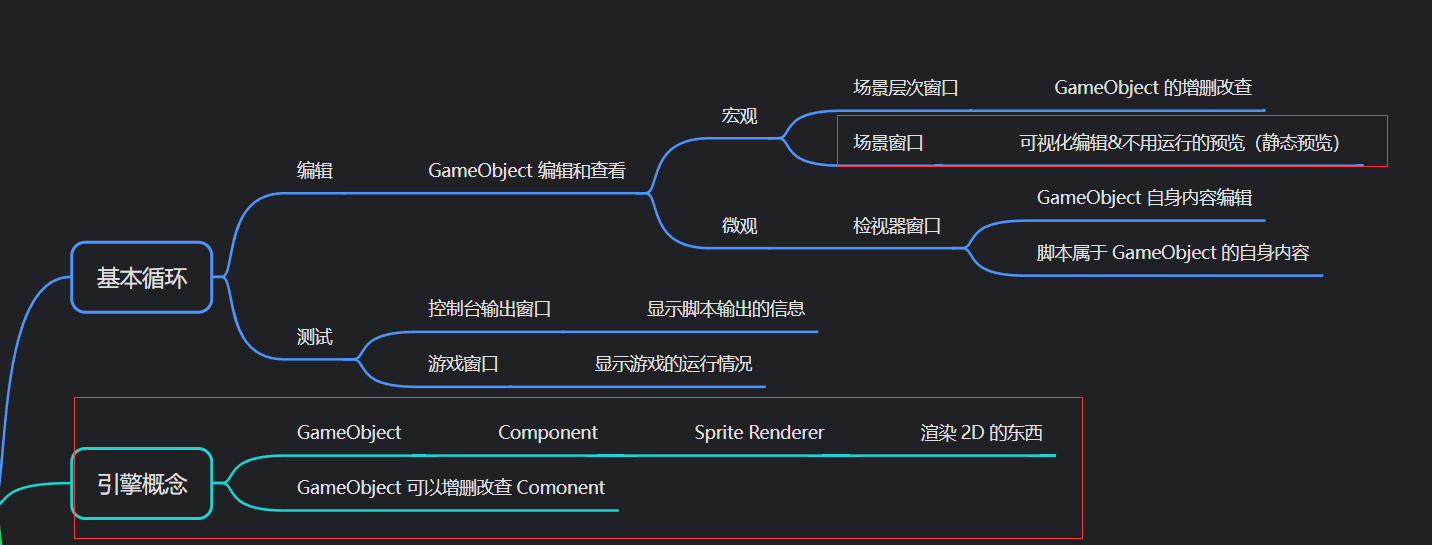
凉鞋的 Unity 笔记 106. 第二轮循环场景视图Sprite Renderer
106. 第二轮循环&场景视图&Sprite Renderer 从这一篇开始,我们开始进行第二轮循环。 这次我们至少能够在游戏运行窗口看到一些东西。 首先还是在场景层次窗口进行编辑,先创建一个 Sprite,操作如下: 创建后,会在 Scene …...

Vue中如何进行分布式路由配置与管理
Vue中的分布式路由配置与管理 随着现代Web应用程序的复杂性不断增加,分布式路由配置和管理成为了一个重要的主题。Vue.js作为一种流行的前端框架,提供了多种方法来管理Vue应用程序的路由。本文将深入探讨在Vue中如何进行分布式路由配置与管理࿰…...
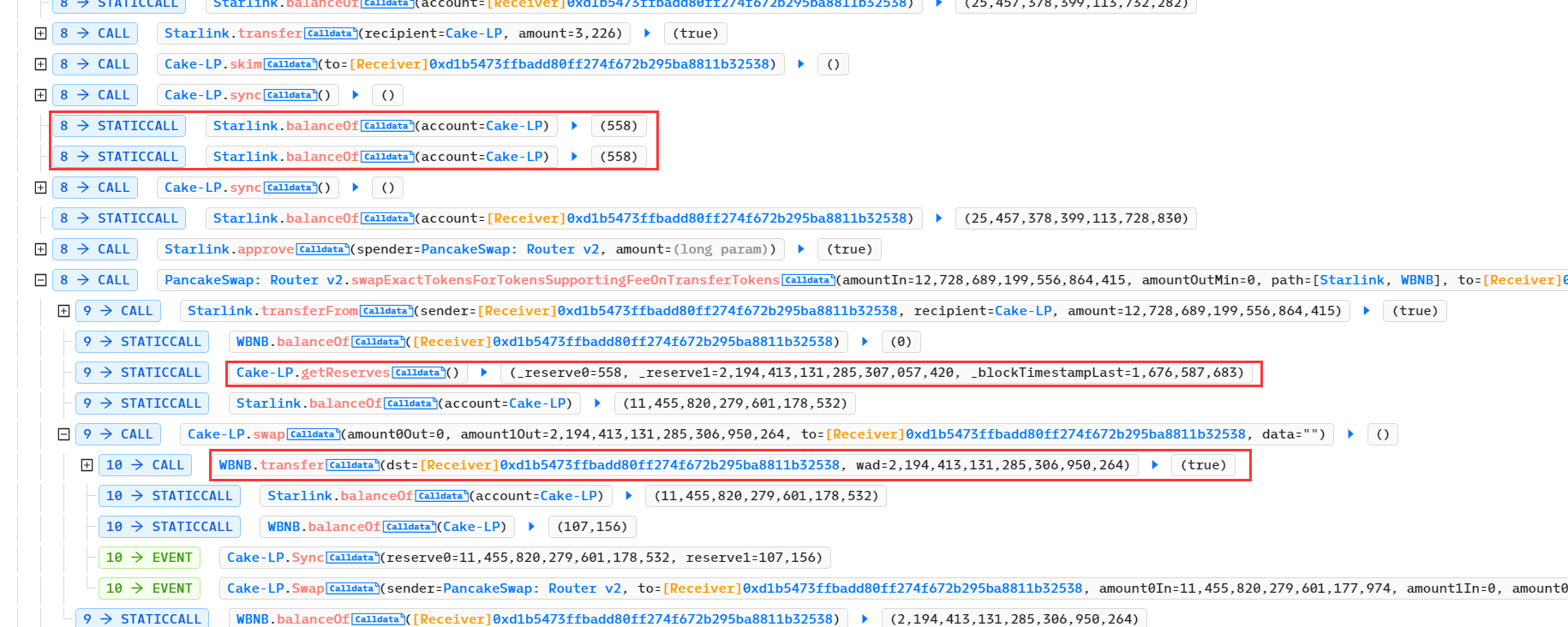
Solidity 合约漏洞,价值 38BNB 漏洞分析
Solidity 合约漏洞,价值 38BNB 漏洞分析 1. 漏洞简介 https://twitter.com/NumenAlert/status/1626447469361102850 https://twitter.com/bbbb/status/1626392605264351235 2. 相关地址或交易 攻击交易: https://bscscan.com/tx/0x146586f05a451313…...
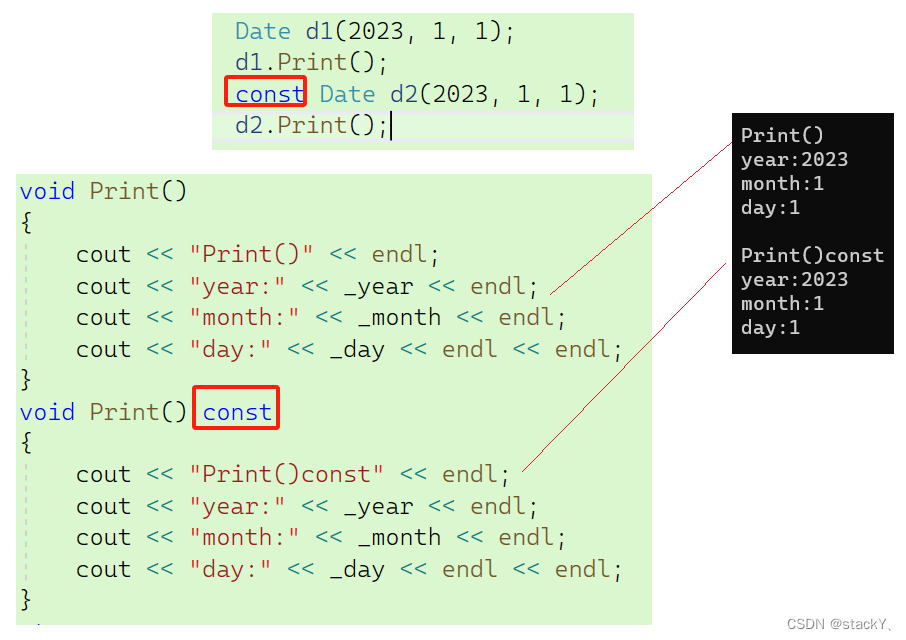
【C++】:类和对象(2)
朋友们、伙计们,我们又见面了,本期来给大家解读一下有关Linux的基础知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从入门到精通 数…...

【GIT版本控制】--提交更改
一、添加文件到暂存区 在GIT中,要提交更改,首先需要将文件添加到暂存区(Staging Area)。这是一个用于存放将要提交的更改的临时区域。以下是将文件添加到暂存区的步骤: 打开终端或命令提示符:首先&#x…...
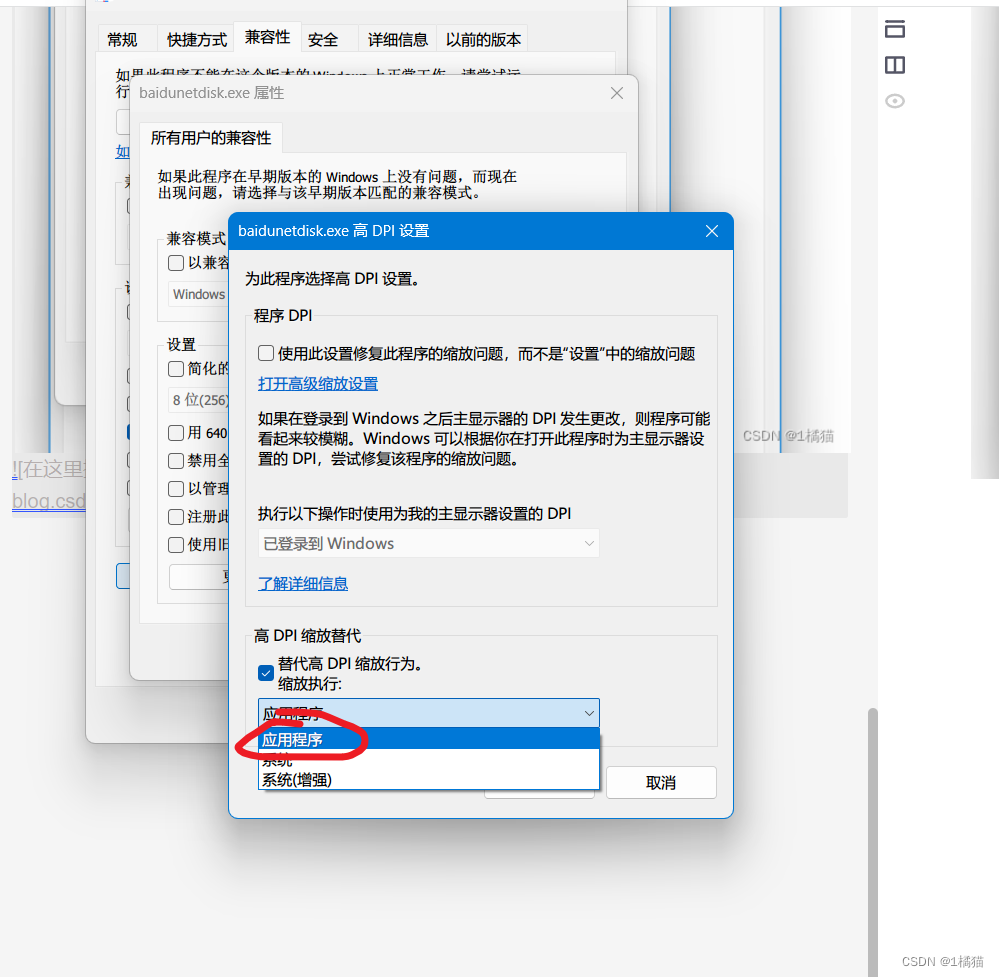
解决高分屏DPI缩放PC端百度网盘界面模糊的问题
第一步 更新最新版本 首先,在百度网盘官网下载最新安装包: https://pan.baidu.com/download 进行覆盖安装 第二步 修改兼容性设置 右键百度网盘图标,点击属性,在兼容性选项卡中点击更改所有用户的设置 弹出的选项卡中选择更改高…...
全能视频工具 VideoProc Converter 4K for mac中文
VideoProc 4K提供快速完备的4K影片处理方案,您可以透过这款软体调节输出影片格式和大小。能够有效压缩HD/4K影片体积90%以上,以便更好更快地上传到YouTube,或是通过电子邮件附件发送。业界领先的视讯压缩引擎,让你轻松处理大体积视…...

Vue中实现自定义编辑邮件发送到指定邮箱(纯前端实现)
formspree里面注册账号 注册完成后进入后台新建项目并且新建表单 这一步完成之后你将得到一个地址 最后就是在项目中请求这个地址 关键代码如下: submitForm() {this.fullscreenLoading true;this.$axios({method: "post",url: "https://xxxxxxx…...

计算机专业毕业设计项目推荐11-博客项目(Go+Vue+Mysql)
博客项目(GoVueMysql) **介绍****系统总体开发情况-功能模块****各部分模块实现** 介绍 本系列(后期可能博主会统一为专栏)博文献给即将毕业的计算机专业同学们,因为博主自身本科和硕士也是科班出生,所以也比较了解计算机专业的毕业设计流程以及模式&am…...

QT实现TCP
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//实例化一个服务器server new QTcpServer(this);// 此时,服务器已经成功进入监听状态,…...
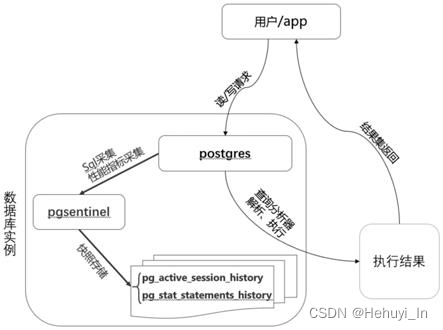
PostgreSQL ash —— pgsentinel插件
一、 插件作用 众所周知,pg是没有像oracle那样的ash视图的,因此要回溯历史问题不太方便。pgsentinel插件会将pg_stat_activity与pg_stat_statements视图内容定期快照,并存入pg_active_session_history和pg_stat_statements_history视图中。 1…...
【刷题笔记10.5】LeetCode:排序链表
LeetCode:排序链表 一、题目描述 给你链表的头结点 head ,请将其按 升序 排列并返回 排序后的链表 。 二、分析 这题咱们默认要求:空间复杂度为O(1)。所以这把咱们用自底向上的方法实现归并排序,则可以达到O(1) 的空间复杂…...
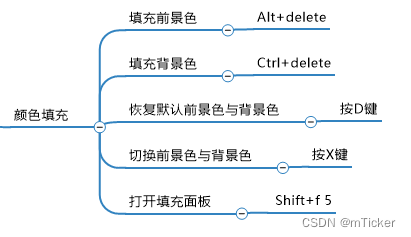
三、【色彩模式与颜色填充】
文章目录 Photoshop常用的几种颜色模式包括:1. RGB模式2. CMYK模式3. 灰度模式4. LAB模式5. 多通道模式 Photoshop颜色填充1.色彩基础2.拾色器认识3.颜色填充最后附上流程图: Photoshop常用的几种颜色模式包括: 1. RGB模式 详细可参考&…...
karmada v1.7.0安装指导
前言 安装心得 经过多种方式操作,发现二进制方法安装太复杂,证书生成及其手工操作太多了,没有安装成功;helm方式的安装,v1.7.0的chart包执行安装会报错,手工修复了报错并修改了镜像地址,还是各…...
OK3568 forlinx系统编译过程及问题汇总
1. 共享文件夹无法加载;通过网上把文件夹加载后,拷贝文件很慢,任务管理器查看发现硬盘读写速率很低。解决办法:重新安装vmware tools。 2. 拷贝Linux源码到虚拟机,解压。 3. 虚拟机基本库安装 forlinxubuntu:~$ sudo…...

JVM篇---第五篇
系列文章目录 文章目录 系列文章目录一、简述Java的对象结构二、如何判断对象可以被回收?三、JVM的永久代中会发生垃圾回收么?一、简述Java的对象结构 Java对象由三个部分组成:对象头、实例数据、对齐填充。 对象头由两部分组成,第一部分存储对象自身的运行时数据:哈希码…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
