推荐算法——Apriori算法原理
0、前言:
- 首先名字别读错:an pu ruo ao rui 【拼音发音】
- Apriori是一种推荐算法
- 推荐系统:从海量数据中,帮助用户进行信息的过滤和选择。主要推荐方法有:基于内容的推荐、协同过滤推荐、基于关联规则的推荐、基于知识的推荐、混合推荐。
- 关联分析:是一种在大规模数据集中寻找有趣关系的非监督学习算法,是利用一些有趣性的量度来识别数据库中发现的强规则。
1、基础概念
- 频繁项集:经常【需要量化】出现在一块的物品的集合
- 关联规则:暗示两种物品之间可能存在很强的关系
- 事务:将数据看成一条条交易记录的集合,事务就是一条交易
- 项:交易的每一个物品称为一个项
- 项集:包含零个或者多个项的集合
- k-项集:包含k个项的项集
- 前件和后件:一个规则中先买了尿布后买了啤酒,尿布就是啤酒的前件、啤酒就是尿布的后件
- 常用频繁项集的评估标准有:支持度、置信度、提升度;
- 支持度就是几个关联的数据在数据集中出现次数占总数据集的比重。(举例:超市一天卖了5单,其中有2单同时出现了尿布和啤酒,那么{尿布、啤酒}的支持度就是2/5=0.4),支持度常用来删除一些没意义的规则。
- 置信度就是一个数据出现后,另一个数据出现的概率。(举例:买了尿布后会买啤酒的概率=两者同时出现的概率(两者的支持度)/尿布出现的概率(尿布的支持度))
- 提升度:如果A事件的支持度本来就很高,然后求B事件发生后A事件的置信度,发现也很高,但并没有A事件本身的支持度高,就有可能误以为B事件的发生导致A事件发生的可能性增加了。所以加入了提升度的概念(举例:求A事件发生对B事件的提升度=AB同时发生的支持度/B事件发生的持度度),提升度大于1,表明A对B是有效的强关联规则,小于1表明A对B是无效的强关联规则。等于1,说明没有提升。
- ★发现频繁项集和关联规则:如果一一遍历去找关联规则和频繁项集,计算量非常大,所以要进行筛选。
- 1、首先设定最小支持度,最小置信度,找到满足最小支持度的所有项集,这些项集叫做频繁项集。
- 2、从频繁项集中提取所有高置信度的规则,这些规则就是强关联规则。
- 注意:如果一个项集是频繁的,那么它的所有子集也是频繁的。
- 注意:如果一个项集是非频繁的,那么所有包含它的集合也是非频繁的。【通过这条规则减少计算量】
2、算法实现过程
- Apriori算法原理:所有非频繁项集不用计算,减少计算量。获取apriori频繁项集是第一步,要通过apriori最终获取强关联规则,就要在频繁项集支持度的基础上,计算每种规则的支持度。

- 原始候选集构建1-项集:
# 数据集
dataset = [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
# 让候选集每一项变成不可变集合,进而获取1-项集
def creat_c1(data_set):c1 = []for data in data_set:for i in data:if i not in c1:c1.append(i)c1.sort()return list(map(frozenset,[{i} for i in c1])) # frozenset是将集合变成不可变集合,目的是最后让frozenset作为字典的key
c1 = creat_c1(dataset)
'''
[frozenset({1}),frozenset({2}),frozenset({3}),frozenset({4}),frozenset({5})]
'''
- 由1-项集(C1)转为1-项频繁集(L1)推出k-项集转k-项频繁集的函数:通过支持度筛选频繁集;scanD()函数:获取所有k-项集的支持度和k-项集对应的k-项频繁集
# C1(1项集):L1(1项频繁项集)
# D:数据集
# Ck:k项集
# min_support:最小支持度
def scanD(D,Ck,min_support=0.1):support_dic = {}# 遍历原始交易记录for d in D:for c in Ck:# 判断是否是子集,是的话数量加1if c.issubset(d):support_dic[c] = support_dic.get(c,0) + 1 # 防止刚开始support_dic是空support_data = {} # 所有项集的支持度LK = [] # 频繁项集# 计算支持度for k,v in support_dic.items():support = v/len(D)support_data[k] = support
# print(support_data) # 打印支持度# 获得频繁项集if support >= min_support:LK.append(k)# 返回频繁项集、所有项集支持度:return LK, support_data
- 由1-项频繁集产生2-项集的方法推出:k-项频繁集产生k+1-项集的方法;apriori_gen()函数:获取所有k-项频繁集(Lk)对应的k+1-项集(Ck+1),如下图以2-项集生成方法说明:

# L1(1频繁项集) => C2(2项集)
def apriori_gen(LK):Ck = []for i in range(len(LK)-1):for j in range(i+1,len(LK)):f_set = LK[i] | LK[j]# print(f_set)# 不能重复,新项集只能是k+1项if f_set not in Ck and len(f_set) == len(LK[0])+1:Ck.append(f_set)# print(Ck)return Ck
- 获取频繁项集和频繁项集生成过程中产生的项集的支持度
import time
def apriori(D, min_support=0.1):c1 = creat_c1(D)L1,support1 = scanD(D,c1,min_support)# 所有频繁项集L_f = []# 所有项集支持度就直接添加到support1中# 循环while True:L_f.append(L1)# 项集C = apriori_gen(L1)# 项集——频繁项集L,support = scanD(D,C,min_support)L1 = Lsupport1.update(support)if len(L1)==0:breakreturn L_f,support1
- 获取k项集满足最小置信度的强关联规则的集合
计算置信度:confidence(X -> Y) = P(Y|X) = P(XY) / P(X)【在x发生的条件下Y发生的置信度】
calculate_conf()函数:计算某个频繁项集对应的满足最小置信度的强关联规则的集合。
# 计算一个项集的所有强关联规则
# 计算置信度
# freqSet: 频繁项集
# H=[frozenset({i}) for i in freqSet]
# L, support_Data = apriori(dataset, min_support=n)
# brl = [ ] # 保存强关联规则的列表
def calculate_conf(freqSet, H, supportData, brl, minConf=0.5):newH = [ ]# 遍历Hfor s in H:# 置信度conf = supportData[freqSet] / supportData[freqSet - s]# conf(3,5->1) = P(1, 3, 5) / P(3,5) # display(f'--- {freqSet - s} -> {s} = {conf} ---')# 大于最小置信度的规则是强规则if conf >= minConf:# 保存强关联规则到brl中brl.append( (freqSet - s, "->" , s, ' = ', conf) ) newH.append(s)return newH用一个2-项集测试下函数calculate_conf,发现对于2-项集,函数能够获取所有满足置信度要求的关联规则。
freqSet = frozenset({1, 3})
H = [frozenset({i}) for i in freqSet]
L, support_data = apriori(dataset, min_support=0.2)
brl = [ ] # 保存强关联规则的列表
# display(freqSet, H)# 计算单个项集的置信度
calculate_conf(freqSet, H, support_data, brl, minConf=0.1)
brl
'''
[(frozenset({3}), '->', frozenset({1}), ' = ', 0.6666666666666666),(frozenset({1}), '->', frozenset({3}), ' = ', 1.0)]
'''
# 3-项集
freqSet = frozenset({1, 3, 5})
H = [frozenset({i}) for i in freqSet]
L, support_data = apriori(dataset, min_support=0.2)
brl = [ ] # 保存强关联规则的列表
# display(freqSet, H)# 计算单个项集的置信度
calculate_conf(freqSet, H, support_data, brl, minConf=0.1)
brl
'''
[(frozenset({3, 5}), '->', frozenset({1}), ' = ', 0.5),(frozenset({1, 5}), '->', frozenset({3}), ' = ', 1.0),(frozenset({1, 3}), '->', frozenset({5}), ' = ', 0.5)]
'''
可以发现:在3项集中出现了问题,3项集中只有2-项集作为前件的情况,没有1-项集作为前件的情况,出现了统计不完全的情况。因此为了让统计结果齐全,需要重新写个函数完善calculate_conf()函数。
# 考虑2-项集,3-项集,4-项集...
def rules_from_freq(freqSet, H, supportData, brl, minConf=0.7):tmp = Truewhile tmp:tmp = False# 计算置信度newH = calculate_conf(freqSet, H, supportData, brl, minConf=minConf)# display(f'newH: {newH}')H = apriori_gen(newH)# display(f'H: {H}')# print('*' * 100)tmp = not (H==[ ] or len(H[0]) == len(freqSet))测试:通过测试结果可以看出,完善之后的函数就能够获得所有满足要求置信度的关联规则
# 3-项集
freqSet = frozenset({1, 3, 5})
H = [frozenset({i}) for i in freqSet]
L, support_data = apriori(dataset, min_support=0.2)
brl = [ ] # 保存强关联规则的列表
# display(freqSet, H)# 计算单个项集的置信度
rules_from_freq(freqSet, H, support_data, brl, minConf=0.1)
brl
'''
[(frozenset({3, 5}), '->', frozenset({1}), ' = ', 0.5),(frozenset({1, 5}), '->', frozenset({3}), ' = ', 1.0),(frozenset({1, 3}), '->', frozenset({5}), ' = ', 0.5),(frozenset({5}), '->', frozenset({1, 3}), ' = ', 0.3333333333333333),(frozenset({3}), '->', frozenset({1, 5}), ' = ', 0.3333333333333333),(frozenset({1}), '->', frozenset({3, 5}), ' = ', 0.5)]
'''
- 获取强关联规则的置信度:获取给定项集L中满足置信度要求的强关联规则
def gen_rules(L, support_data, min_conf=0.5):big_rule_list = [ ]for i in range(1, len(L)): # 遍历所有行,第一行除外for freqSet in L[i]: # 遍历每一行的所有元素# display(freqSet)H = [frozenset({i}) for i in freqSet]# 求每个项集的强关联规则,会保存在big_rule_list中rules_from_freq(freqSet, H, support_data, big_rule_list, minConf=min_conf)return big_rule_list
3、apriori算法总结:通过总结疏通下apriori算法中求频繁项集和求强关联规则的函数构造方法

相关文章:

推荐算法——Apriori算法原理
0、前言: 首先名字别读错:an pu ruo ao rui 【拼音发音】Apriori是一种推荐算法推荐系统:从海量数据中,帮助用户进行信息的过滤和选择。主要推荐方法有:基于内容的推荐、协同过滤推荐、基于关联规则的推荐、基于知识的…...

vue ant 隐藏 列
vue ant 隐藏 列 如果你使用的是Vue和Ant Design Vue组件库,你可以使用v-if指令来实现条件渲染来隐藏列。以下是一个示例代码: <template><a-table :columns"columns" :data-source"data"><template v-slot:custom…...

java基础之初始化顺序
初始化顺序 在类中变量定义的顺序决定了它们初始化的顺序。在创建任何java对象时,都是依次调用父类非静态初始化块、父类构造器执行初始化、本类的非静态初始化块、本类构造器执行初始化 public class House { // 构造器之前 Window w1 new Window(1); Ho…...
FFmpeg 命令:从入门到精通 | ffmpeg filter(过滤器 / 滤镜)
FFmpeg 命令:从入门到精通 | ffmpeg filter(过滤器 / 滤镜) FFmpeg 命令:从入门到精通 | ffmpeg filter(过滤器 / 滤镜)ffmpeg fliter 基本内置变量视频裁剪文字水印图片水印画中画视频多宫格处理 FFmpeg 命…...

【C语言】23-结构体类型
目录 1. 如何建立结构体类型2. 如何使用结构体2.1 定义结构体变量2.2 结构体变量的初始化和引用2.3 结构体数组2.4 结构体指针2.4.1 指向结构体变量的指针2.4.2 指向结构体数组的指针C 语言提供了一些由系统已定义好的数据类型,如: int、 float、 char 等,用户可以在程序…...

Python小技巧:快速合并字典dict()
文章目录 前言知识点字典合并1. dict.update()基础合并2. 字典推导式 update() 后话 前言 这里是Python小技巧的系列文章。这是第四篇,快速合并字典。 在Python的使用中,有时候需要将两个 dict(字典) 进行合并。 通常我们会借助 dict(字典) 的内置方法 …...
)
如何使用 React 和 Docusaurus 编写的一些自定义钩子(Hook)
import useRouteContext from @docusaurus/useRouteContext; import {DependencyList, useEffect, useRef, useState, useMemo } from react; import {dequal } from dequal; /* eslint-disable global-require */ // @ts-ignore/*** 用于深度检测依赖的useMemo钩子* @param fa…...

【初识Linux】Linux环境配置、Linux的基本指令 一
Linux基本指令一 一、学习前提(环境配置)①安装Xshell和云服务器推荐②Xshell用途如下图③打开Xshell 二、 Linux基本指令①whoami和who指令②pwd、ls、ls -l三个指令ls指令扩充 ③cd指令前提了解有了上面的认识,我们就可以开始cd指令的学习了 ④tree指令…...

conda常用命令参数,指定版本,依赖库文件,创建虚拟环境,删除,激活,退出,内部安装包,pip通过代理安装包
以下是conda的常用命令和参数: 1. 创建虚拟环境: - 创建一个新的虚拟环境:conda create -n 环境名 pythonx.x - 使用指定的依赖文件创建虚拟环境:conda create -n 环境名 --file requirements.txt 2. 激活虚拟环境&#x…...
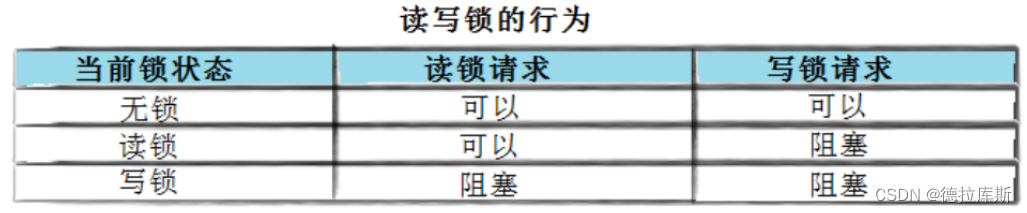
【锁的区别】C++线程库和POSIX线程库锁的区别
C线程库和POSIX线程库锁的区别 C线程库代码段的互斥:mutex、recursive_mutex、timed_mutex、recursive_timed_mutex互斥量mutex:直接进行lock()或者unlock()递归互斥锁recursive_mutex:可以多次加锁,意味着加几次锁就需要解几次锁…...

网络层·IP协议
承接前文TCP协议-CSDN博客 简介 协议头格式 网段划分(重要) 划分方法 IP地址的数量限制(背景介绍) 私有IP地址和公网IP地址(提出解决思路) NAT技术(解决方法) 路由 网络层 在复杂的网络环境中确定一个合适的路径 IP协议 主机: 配有IP地址, 可以认为就是你的电脑; 路由器:…...
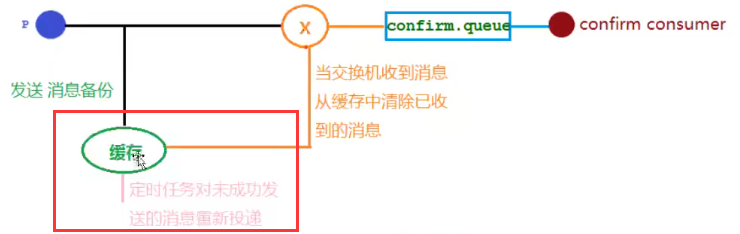
RabbitMQ学习笔记(下):延迟队列,发布确认高级,备份交换机
十、延迟队列 延迟队列 概念: 延迟队列使用场景: 流程图: 延迟队列整合Springboot 导入依赖: <dependencies><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot…...

Python 无废话-基础知识面向对象编程详解
类定义 如何理解万物皆对象? 生活中一些事物,动物(可爱的小狗、调皮的小猫)、交通工具(比亚迪U8汽车、飞机)、人(学生、教师)…… 这些对象都有着独特或共性的属性和方法来描述其…...
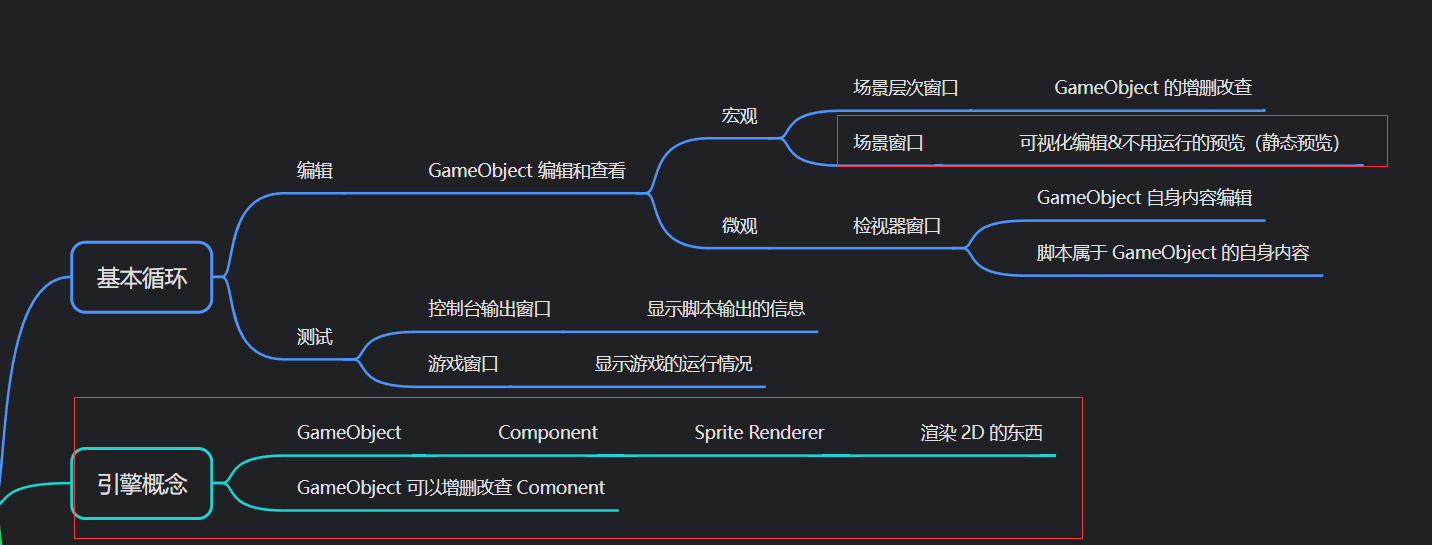
凉鞋的 Unity 笔记 106. 第二轮循环场景视图Sprite Renderer
106. 第二轮循环&场景视图&Sprite Renderer 从这一篇开始,我们开始进行第二轮循环。 这次我们至少能够在游戏运行窗口看到一些东西。 首先还是在场景层次窗口进行编辑,先创建一个 Sprite,操作如下: 创建后,会在 Scene …...

Vue中如何进行分布式路由配置与管理
Vue中的分布式路由配置与管理 随着现代Web应用程序的复杂性不断增加,分布式路由配置和管理成为了一个重要的主题。Vue.js作为一种流行的前端框架,提供了多种方法来管理Vue应用程序的路由。本文将深入探讨在Vue中如何进行分布式路由配置与管理࿰…...
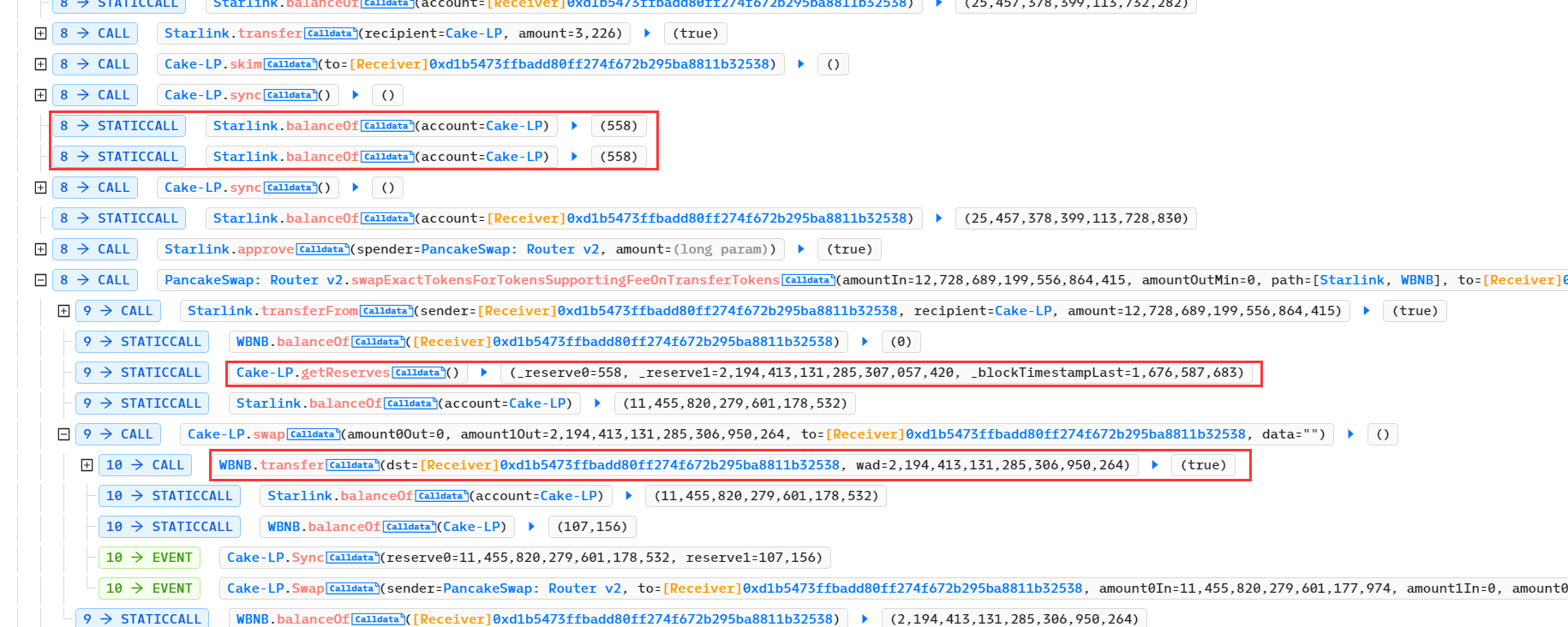
Solidity 合约漏洞,价值 38BNB 漏洞分析
Solidity 合约漏洞,价值 38BNB 漏洞分析 1. 漏洞简介 https://twitter.com/NumenAlert/status/1626447469361102850 https://twitter.com/bbbb/status/1626392605264351235 2. 相关地址或交易 攻击交易: https://bscscan.com/tx/0x146586f05a451313…...
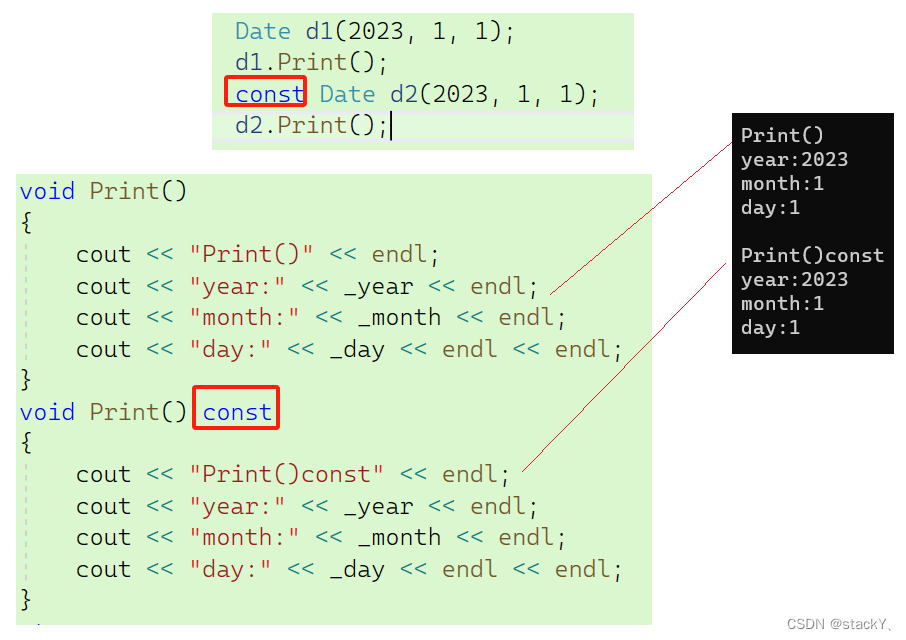
【C++】:类和对象(2)
朋友们、伙计们,我们又见面了,本期来给大家解读一下有关Linux的基础知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从入门到精通 数…...

【GIT版本控制】--提交更改
一、添加文件到暂存区 在GIT中,要提交更改,首先需要将文件添加到暂存区(Staging Area)。这是一个用于存放将要提交的更改的临时区域。以下是将文件添加到暂存区的步骤: 打开终端或命令提示符:首先&#x…...
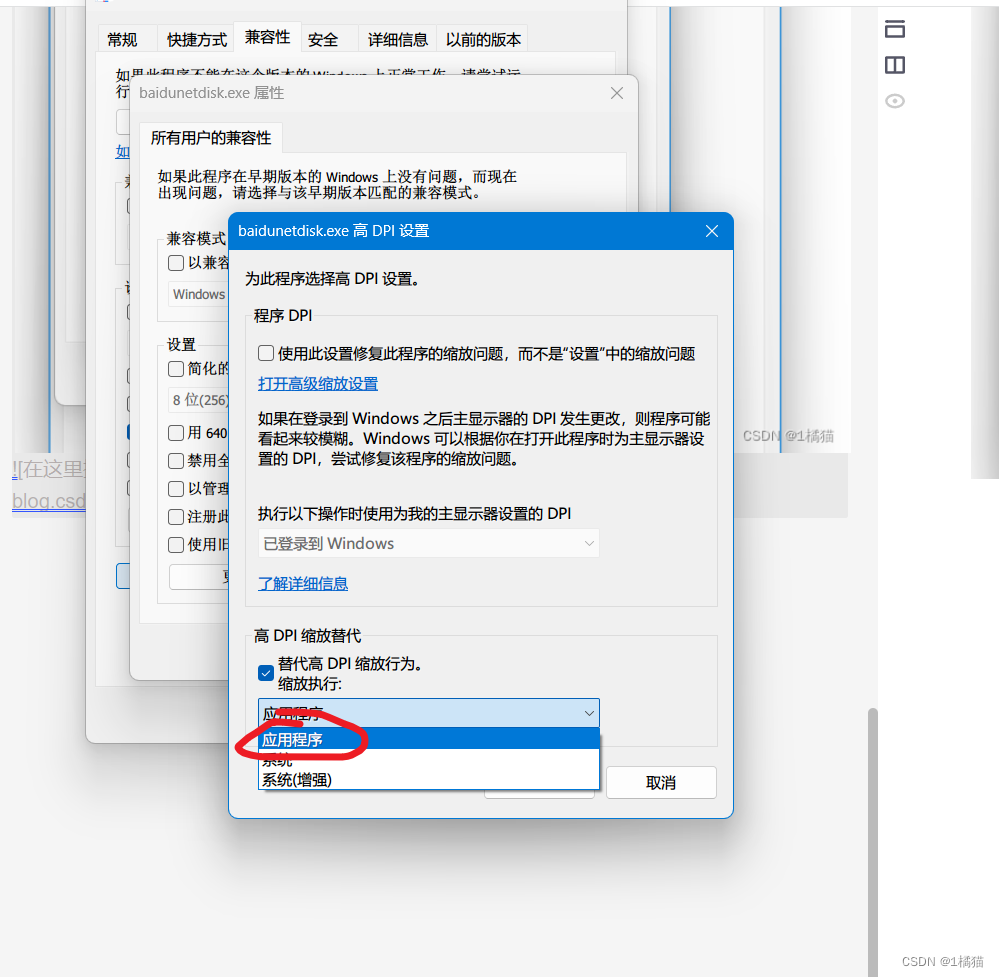
解决高分屏DPI缩放PC端百度网盘界面模糊的问题
第一步 更新最新版本 首先,在百度网盘官网下载最新安装包: https://pan.baidu.com/download 进行覆盖安装 第二步 修改兼容性设置 右键百度网盘图标,点击属性,在兼容性选项卡中点击更改所有用户的设置 弹出的选项卡中选择更改高…...
全能视频工具 VideoProc Converter 4K for mac中文
VideoProc 4K提供快速完备的4K影片处理方案,您可以透过这款软体调节输出影片格式和大小。能够有效压缩HD/4K影片体积90%以上,以便更好更快地上传到YouTube,或是通过电子邮件附件发送。业界领先的视讯压缩引擎,让你轻松处理大体积视…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
