折半+dp之限制转状态+状压:CF1767E
https://vjudge.net/problem/CodeForces-1767E/origin
首先40,必然折半。然后怎么做?
分析性质。每次可以走1步or2步,等价什么?等价任意相邻2个必选一个!然后就可以建图
这个图是个限制图,我们折半后可以进行状压。dp的过程是限制转状态。
首先分别的,前后内部都必须满足。然后对于交织在两部分的限制,我们枚举其中一边哪些不选,必然可以对应另外那边哪些必选。得到的集合求其最小合法超集即是答案。
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 300010
#define M 21
//#define mo
int n, m, i, j, k, T;
int ans, f[1<<M], b[M<<1][M<<1];
int a[N], s, t, mid, cost[M<<1];
int k1, k2, s1, s2; void cun(int x, int y) {b[x][y]=b[y][x]=1;
}int check(int s) {if(k1<mid && (s&s1)==0) return 0; if(k2<mid && (s&s2)==0) return 0; for(int i=0; i<mid; ++i)for(int j=0; j<mid; ++j)if(b[i][j] && (!(s&(1<<i)) && !(s&(1<<j)))) return 0; return 1;
}int check2(int s) {if(k1>=mid && (s&s1)==0) return 0; if(k2>=mid && (s&s2)==0) return 0; for(int i=mid; i<m; ++i)for(int j=mid; j<m; ++j) if(b[i][j] && (!(s&(1<<i-mid)) && !(s&(1<<j-mid)))) return 0; return 1;
}void Least(int s, int &t) {for(int i=mid; i<m; ++i)for(int j=0; j<mid; ++j) {
// printf("(%d %d) %d\n", i, j); if(b[i][j] && !(s&(1<<i-mid))) t|=(1<<j); }}signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);
// T=read();
// while(T--) {
//
// }n=read(); m=read(); mid=m/2; ans=1e18;
// printf("%lld\n", mid); for(i=1; i<=n; ++i) a[i]=read()-1; s1=(1<<a[1]); s2=(1<<a[n]); k1=a[1]; k2=a[n]; if(k1>=mid) s1=(1<<a[1]-mid); if(k2>=mid) s2=(1<<a[n]-mid);
// printf("%d %d | %d %d\n", k1, k2, s1, s2); for(i=1; i<n; ++i) cun(a[i], a[i+1]); for(i=0; i<m; ++i) cost[i]=read(); memset(f, 0x3f, sizeof(f)); for(s=(1<<mid)-1; s>=0; --s) {if(check(s)) {
// printf("> %d ", s); for(i=k=0; i<mid; ++i) if(s&(1<<i)) k+=cost[i];
// printf("%lld\n", k); f[s]=min(f[s], k); }for(i=0; i<mid; ++i) if(s&(1<<i))f[s-(1<<i)]=min(f[s-(1<<i)], f[s]); }for(s=0; s<(1<<m-mid); ++s) {if(check2(s)) {
// printf(">> %d ", s);t=0; Least(s, t); for(i=k=0; i<m-mid; ++i) if(s&(1<<i)) k+=cost[i+mid];
// printf("%lld %lld\n", k, t); ans=min(ans, k+f[t]); }}printf("%lld", ans); return 0;
}相关文章:

折半+dp之限制转状态+状压:CF1767E
https://vjudge.net/problem/CodeForces-1767E/origin 首先40,必然折半。然后怎么做? 分析性质。每次可以走1步or2步,等价什么?等价任意相邻2个必选一个!然后就可以建图 这个图是个限制图,我们折半后可以…...

如何写出优质代码
(本文转载自其他博主但是个人忘记了出处) 优质代码是什么? 优质代码是指那些易于理解、易于维护、可读性强、结构清晰、没有冗余、运行效率高、可复用性强、稳定性好、可扩展性强的代码。 这类代码不仅能够准确执行预期功能,同时也便于其他开发者理解…...
ChatGLM2-6B的通透解析:从FlashAttention、Multi-Query Attention到GLM2的微调、源码解读
前言 本文最初和第一代ChatGLM-6B的内容汇总在一块,但为了阐述清楚FlashAttention、Multi-Query Attention等相关的原理,以及GLM2的微调、源码解读等内容,导致之前那篇文章越写越长,故特把ChatGLM2相关的内容独立抽取出来成本文 …...
3D人脸生成的论文
一、TECA 1、论文信息 2、开源情况:comming soon TECA: Text-Guided Generation and Editing of Compositional 3D AvatarsGiven a text description, our method produces a compositional 3D avatar consisting of a mesh-based face and body and NeRF-based ha…...

解决问题:可以用什么方式实现自动化部署
自动化部署可以使用多种工具来实现: 脚本编写:可以使用 Bash、Python 等编写脚本来实现自动化部署。例如,可以使用 Bash 脚本来自动安装、配置和启动应用程序。 配置管理工具:像 Ansible、Puppet、Chef、Salt 等配置管理工具可以…...

【数据结构】链表栈
目录: 链表栈 1. 链式栈的实现2. 链表栈的创建3. 压栈4. 弹栈 链表栈 栈的主要表示方式有两种,一种是顺序表示,另一种是链式表示。本文主要介绍链式表示的栈。 链栈实际上和单链表差别不大,唯一区别就在于只需要对链表限定从头…...

Android笔记:Android 组件化方案探索与思考
组件化项目,通过gradle脚本,实现module在编译期隔离,运行期按需加载,实现组件间解耦,高效单独调试。 先来一张效果图 组件化初衷 APP版本不断的迭代,新功能的不断增加,业务也会变的越来越复杂…...
MeterSphere v2.10.X-lts 双节点HA部署方案
一、MeterSphere高可用部署架构及服务器配置 1.1 服务器信息 序号应用名称操作系统要求配置要求描述1负载均衡器CentOS 7.X /RedHat 7.X2C,4G,200GB部署Nginx,实现负载路由。 部署NFS服务器。2MeterSphere应用节点1CentOS 7.X /RedHat 7.X8C,16GB,200G…...
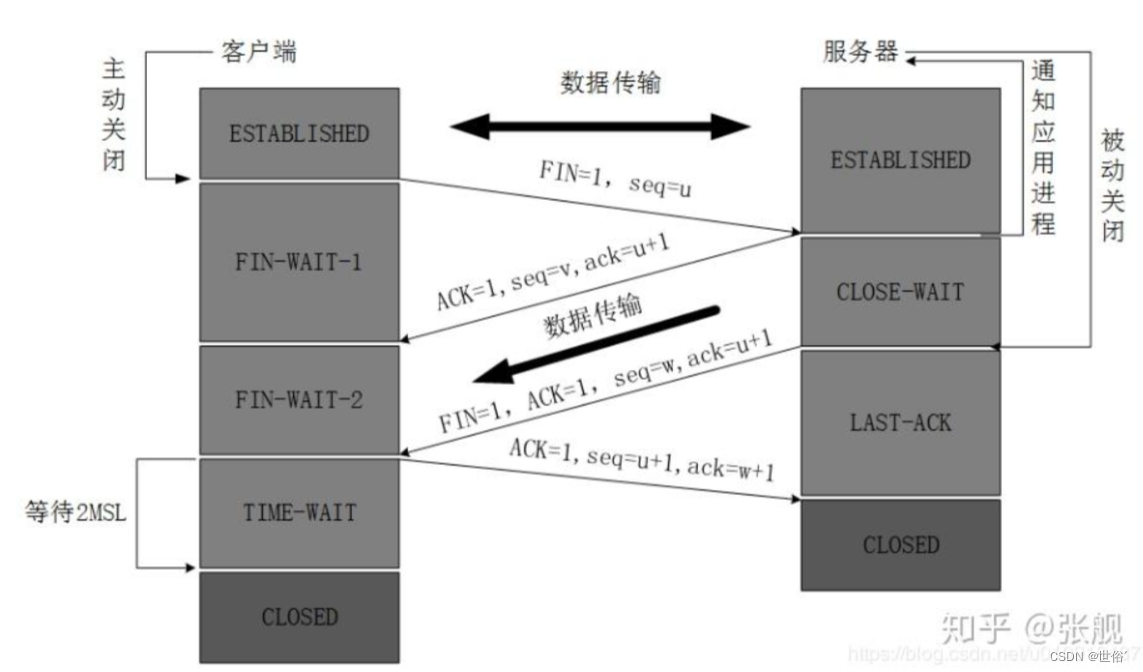
Java进阶篇--网络编程
目录 计算机网络体系结构 什么是网络协议? 为什么要对网络协议分层? 网络通信协议 TCP/IP 协议族 应用层 运输层 网络层 数据链路层 物理层 TCP/IP 协议族 TCP的三次握手四次挥手 TCP报文的头部结构 三次握手 四次挥手 …...

PyTorch入门之【CNN】
参考:https://www.bilibili.com/video/BV1114y1d79e/?spm_id_from333.999.0.0&vd_source98d31d5c9db8c0021988f2c2c25a9620 书接上回的MLP故本章就不详细解释了 目录 traintest train import torch from torchvision.transforms import ToTensor from torchvi…...

马斯洛需求层次模型之安全需求之云安全浅谈
在互联网云服务领域,安全需求是用户首要考虑的因素之一。用户希望在将数据和信息托付给云服务提供商时,这些数据和信息能够得到充分的保护,避免遭受未经授权的访问、泄露或破坏。这种安全需求的满足,对于用户来说是至关重要的&…...
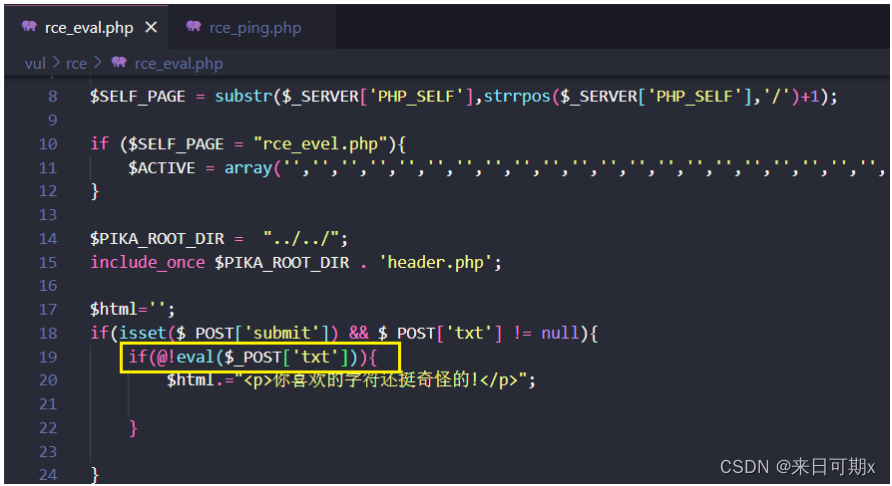
Pikachu靶场——远程命令执行漏洞(RCE)
文章目录 1. RCE1.1 exec "ping"1.1.1 源代码分析1.1.2 漏洞防御 1.2 exec "eval"1.2.1 源代码分析1.2.2 漏洞防御 1.3 RCE 漏洞防御 1. RCE RCE(remote command/code execute)概述: RCE漏洞,可以让攻击者直接向后台服务器远程注入…...
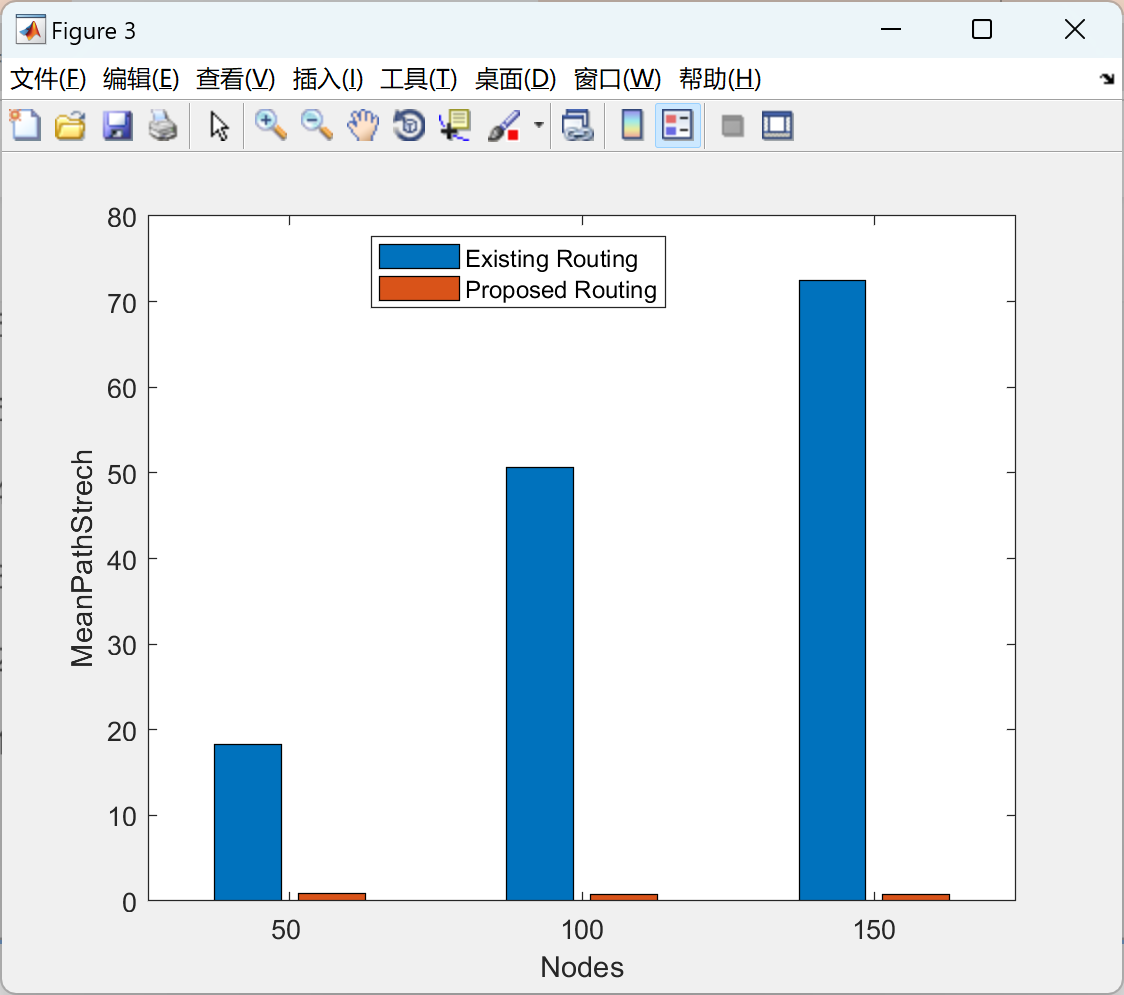
【WSN】无线传感器网络 X-Y 坐标到图形视图和位字符串前缀嵌入方法研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Linux定时任务
文章目录 前言设置定时任务流程定时规则例子 终止定时任务列出当前的定时任务重启任务调度 前言 在Linux系统中有时侯需要周期性的自动执行一些命令,这时候Linux定时任务就派上用场了 设置定时任务流程 进入定时任务的编辑模式 crontab -e编辑定时任务ÿ…...
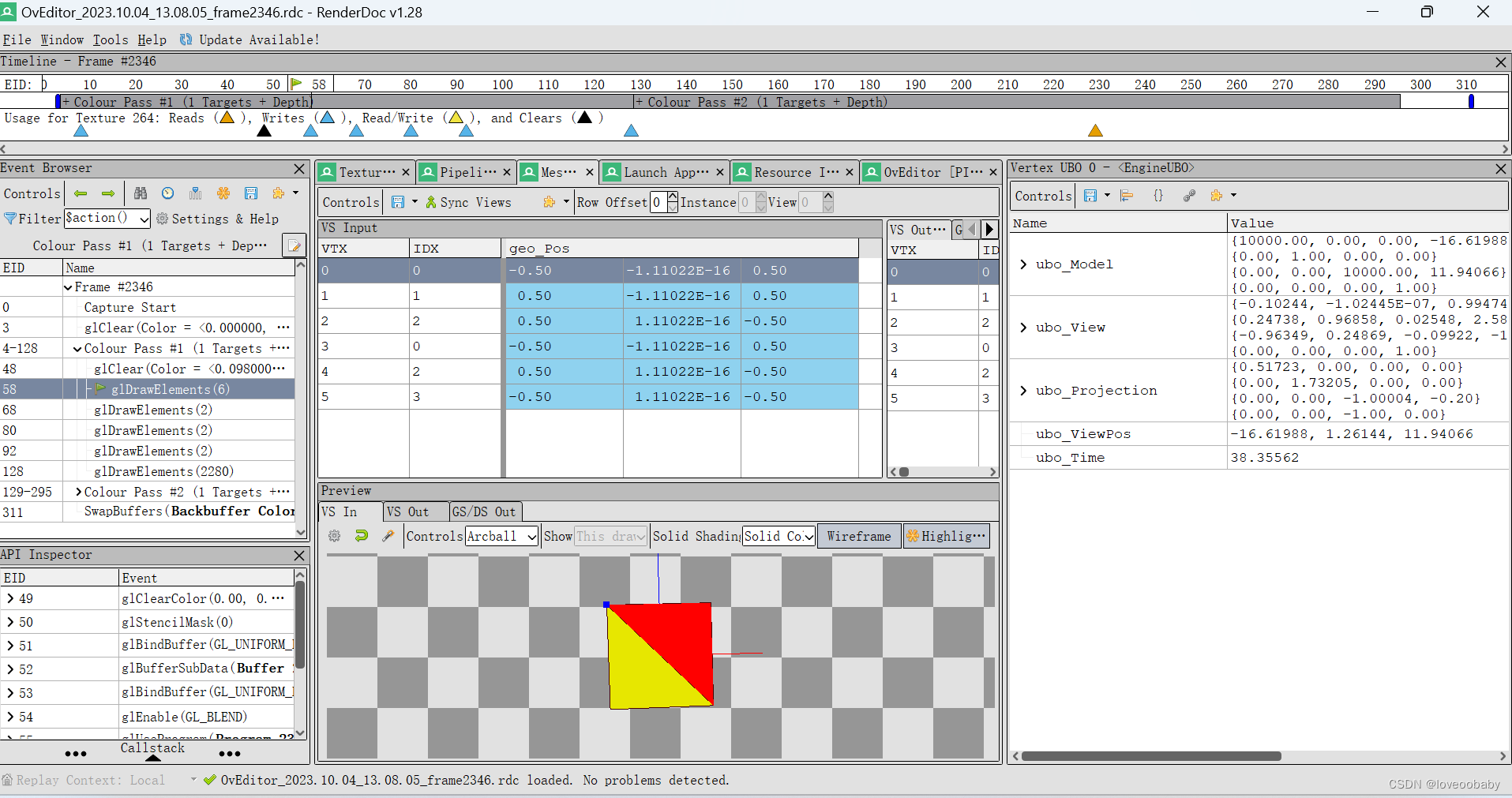
【Overload游戏引擎分析】画场景网格的Shader
Overload引擎地址: GitHub - adriengivry/Overload: 3D Game engine with editor 一、栅格绘制基本原理 Overload Editor启动之后,场景视图中有栅格线,这个在很多软件中都有。刚开始我猜测它应该是通过绘制线实现的。阅读代码发现࿰…...

【JavaEE】多线程进阶(一)饿汉模式和懒汉模式
多线程进阶(一) 文章目录 多线程进阶(一)单例模式饿汉模式懒汉模式 本篇主要引入多线程进阶的单例模式,为后面的大冰山做铺垫 代码案例介绍 单例模式 非常经典的设计模式 啥是设计模式 设计模式好比象棋中的 “棋谱”…...
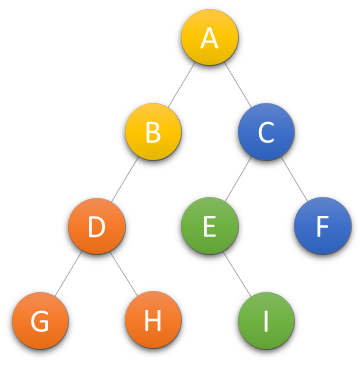
C++树详解
树 树的定义 树(Tree)是n(n≥0)个结点的有限集。n0时称为空树。在任意一颗非空树中:①有且仅有一个特定的称为根(Root)的结点;②当n>1时,其余结点可分为m(…...

支付环境安全漏洞介绍
1、平台支付逻辑全流程分析 2、平台支付漏洞如何利用?买东西还送钱? 3、BURP抓包分析修改支付金额,伪造交易状态? 4、修改购物车参数实现底价购买商品 5、SRC、CTF、HW项目月入10W副业之路 6、如何构建最适合自己的网安学习路线 1…...
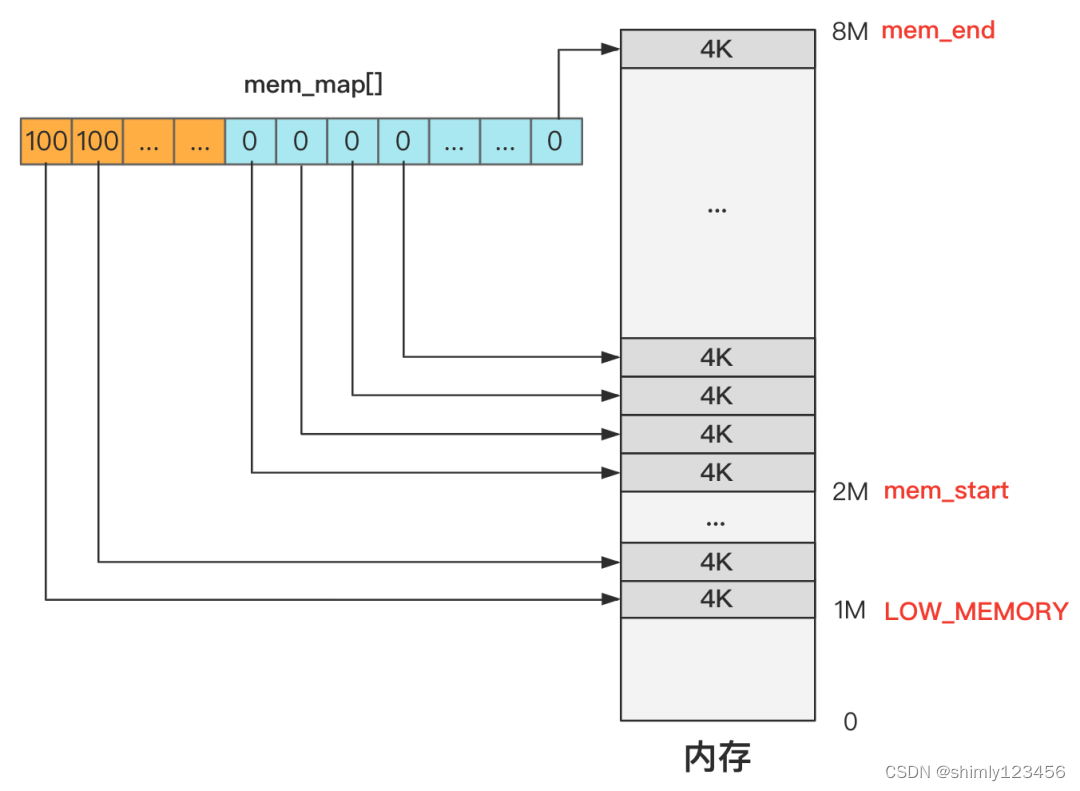
抄写Linux源码(Day16:内存管理)
回忆我们需要做的事情: 为了支持 shell 程序的执行,我们需要提供: 1.缺页中断(不理解为什么要这个东西,只是闪客说需要,后边再说) 2.硬盘驱动、文件系统 (shell程序一开始是存放在磁盘里的,所以需要这两个东…...

Cookie和Session详解以及结合生成登录效果
目录 引言 1.Cookie中的数据从哪来数据长啥样? 2.Cookie有什么作用? 3.cookie与session的工作关联? 4.Cookie到哪去? 5.Cookie如何存? 6.Session 7.Cookie与Session的关联与区别 8.通过代码理解 8.1 相关代码 8.2…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
