JAVA经典百题之找完数
题目:一个数如果恰好等于它的因子之和,这个数就称为"完数"。例如6=1+2+3.编程找出1000以内的所有完数。
程序分析
首先,我们需要编写一个程序来找出1000以内的所有完数。"完数"是指一个数等于它的因子之和,因此,我们需要遍历每个数,计算它的因子并检查是否满足这个条件。
解题思路
我们可以使用三种不同的方法来实现这个程序:
-
暴力法:对每个数进行因子分解,并检查是否满足完数条件。
-
优化暴力法:减少因子的搜索范围,通过观察发现因子一定在 1 到 sqrt(n) 之间。
-
欧几里得算法:利用数论知识,将因子的搜索范围缩小到 sqrt(n) 以内。
1. 暴力法
程序实现
import java.util.ArrayList;
import java.util.List;public class PerfectNumbers {public static boolean isPerfect(int num) {int sum = 1; // 1 is always a factor of any numberfor (int i = 2; i <= num / 2; i++) {if (num % i == 0) {sum += i;}}return (sum == num);}public static List<Integer> findPerfectNumbers(int limit) {List<Integer> perfectNumbers = new ArrayList<>();for (int i = 2; i <= limit; i++) {if (isPerfect(i)) {perfectNumbers.add(i);}}return perfectNumbers;}public static void main(String[] args) {int limit = 1000;List<Integer> perfectNumbers = findPerfectNumbers(limit);System.out.println("Perfect numbers within 1 to " + limit + ": " + perfectNumbers);}
}
优缺点
-
优点:
- 实现简单,容易理解。
-
缺点:
- 算法效率较低,时间复杂度为 O(n^2),对于较大范围的数需要大量计算。
2. 优化暴力法
程序实现
import java.util.ArrayList;
import java.util.List;public class PerfectNumbers {public static boolean isPerfect(int num) {int sum = 1; // 1 is always a factor of any numberfor (int i = 2; i <= Math.sqrt(num); i++) {if (num % i == 0) {sum += i;if (i != num / i) {sum += num / i;}}}return (sum == num);}public static List<Integer> findPerfectNumbers(int limit) {List<Integer> perfectNumbers = new ArrayList<>();for (int i = 2; i <= limit; i++) {if (isPerfect(i)) {perfectNumbers.add(i);}}return perfectNumbers;}public static void main(String[] args) {int limit = 1000;List<Integer> perfectNumbers = findPerfectNumbers(limit);System.out.println("Perfect numbers within 1 to " + limit + ": " + perfectNumbers);}
}
优缺点
-
优点:
- 优化了因子的搜索范围,时间复杂度为 O(n*sqrt(n)),比暴力法效率高。
-
缺点:
- 仍然需要对每个数进行因子分解,效率仍然不是最优。
3. 欧几里得算法
程序实现
import java.util.ArrayList;
import java.util.List;public class PerfectNumbers {public static boolean isPerfect(int num) {if (num <= 1)return false;int sum = 1; // 1 is always a factor of any numberfor (int i = 2; i * i <= num; i++) {if (num % i == 0) {sum += i;if (i != num / i) {sum += num / i;}}}return (sum == num);}public static List<Integer> findPerfectNumbers(int limit) {List<Integer> perfectNumbers = new ArrayList<>();for (int i = 2; i <= limit; i++) {if (isPerfect(i)) {perfectNumbers.add(i);}}return perfectNumbers;}public static void main(String[] args) {int limit = 1000;List<Integer> perfectNumbers = findPerfectNumbers(limit);System.out.println("Perfect numbers within 1 to " + limit + ": " + perfectNumbers);}
}
优缺点
-
优点:
- 采用了更优化的因子搜索范围,时间复杂度为 O(n*sqrt(n)/log(n)),效率比前两种方法更高。
-
缺点:
- 需要理解欧几里得算法,可能对于初学者有一定难度。
总结
-
在这个问题中,欧几里得算法是最优的选择,具有较高的效率和较小的时间复杂度。它通过缩小因子搜索范围,减少了不必要的计算,使得程序更高效。
-
如果对于简单问题或者不追求高效率,暴力法是一种简单易懂的解决方案。
-
优化暴力法介于两者之间,比暴力法效率高,但比欧几里得算法略逊一筹。可根据实际情况选择使用。
综上所述,推荐使用欧几里得算法来解决这个问题。
相关文章:

JAVA经典百题之找完数
题目:一个数如果恰好等于它的因子之和,这个数就称为"完数"。例如61+2+3.编程找出1000以内的所有完数。 程序分析 首先,我们需要编写一个程序来找出1000以内的所有完数。"完数"是指一个数等于它的…...

CSS 滚动驱动动画 view-timeline-inset
view-timeline-inset 语法例子🌰 正 scroll-padding 为正正的 length正的 percentage 负 scroll-padding 为负负的 length负的 percentage 兼容性 view-timeline-inset 在使用 view() 时说过, 元素在滚动容器的可见性推动了 view progress timeline 的进展. 默认…...

ansible部署二进制k8s
简介 GitHub地址: https://github.com/chunxingque/ansible_install_k8s 本脚本通过ansible来快速安装和管理二进制k8s集群;支持高可用k8s集群和单机k8s集群地部署;支持不同版本k8s集群部署,一般小版本的部署脚本基本是通用的。 …...
Nginx限流熔断
一、Nginx限流熔断 Nginx 是一款流行的反向代理和负载均衡服务器,也可以用于实现服务熔断和限流。通过使用 Nginx 的限流和熔断模块,比如:ngx_http_limit_req_module 和 ngx_http_limit_conn_module,可以在代理层面对服务进行限流…...

QQ登录的具体流程
文章目录 网站授权QQ登录QQ登录的完整流程代码示例1. 添加依赖2. 配置文件3. 实现Service4. 创建Controller 网站授权QQ登录 首先需要去QQ互联申请应用填写网站的相关信息,以及回调地址,需要进行审核。申请流程暂时不说了,百度一下挺多申请失…...
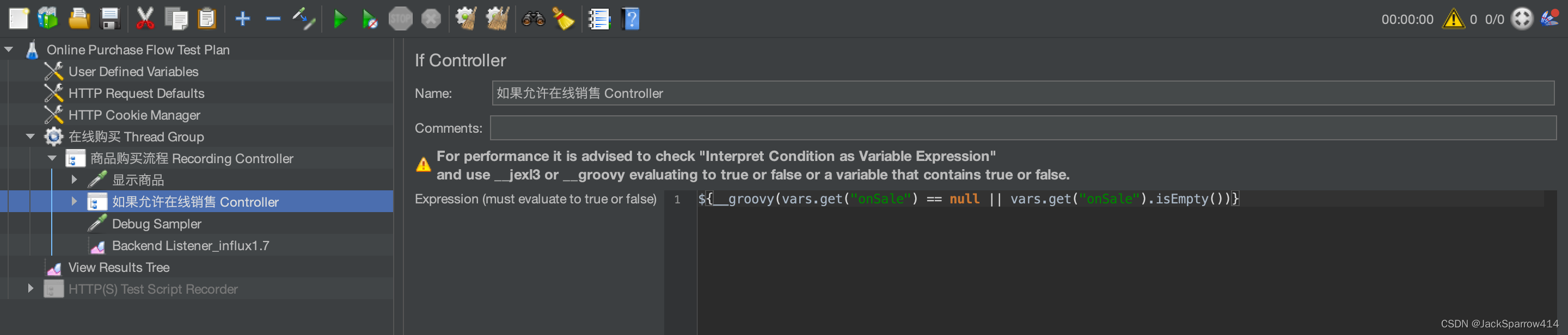
用JMeter对HTTP接口进行压测(一)压测脚本的书写、调试思路
文章目录 安装JMeter和Groovy为什么选择Groovy? 压测需求以及思路准备JMeter脚本以及脚本正确性验证使用Test Script Recorder来获取整条业务线上涉及的接口为什么使用Test Script Recorder? 配置Test Script Recorder对接口进行动态化处理处理全局变量以…...

接着聊聊如何从binlog文件恢复误delete的数据,模拟Oracle的闪回功能
看腻了文章就来听听视频演示吧:https://www.bilibili.com/video/BV1cV411A7iU/ delete忘加where条件(模拟Oracle闪回) 操作基本等同于上篇:再来谈谈如何从binlog文件恢复误update的数据,模拟Oracle的回滚功能 原理&a…...

计算机竞赛 深度学习机器视觉车道线识别与检测 -自动驾驶
文章目录 1 前言2 先上成果3 车道线4 问题抽象(建立模型)5 帧掩码(Frame Mask)6 车道检测的图像预处理7 图像阈值化8 霍夫线变换9 实现车道检测9.1 帧掩码创建9.2 图像预处理9.2.1 图像阈值化9.2.2 霍夫线变换 最后 1 前言 🔥 优质竞赛项目系列,今天要分…...

pyqt5使用经验总结
pyqt5环境配置注意: 安装pyqt5 pip install PyQt5 pyqt5-tools 环境变量-创建变量名: 健名:QT_QPA_PLATFORM_PLUGIN_PATH 值为:Lib\site-packages\PyQt5\Qt\plugins pyqt5经验2: 使用designer.exe进行设计࿱…...

【MQTT】mosquitto库中SSL/TLS相关API接口
文章目录 1.相关API1.1 mosquitto_tls_set1.2 mosquitto_tls_insecure_set1.3 mosquitto_tls_opts_set1.4 mosquitto_tls_insecure_set1.5 mosquitto_tls_set_context1.6 mosquitto_tls_psk_set 2.示例代码 Mosquitto 是一个流行的 MQTT 消息代理(broker)…...
假期题目整合
1. 下载解压题目查看即可 典型的猪圈密码只需要照着输入字符解开即可得到答案 2. 冷门类型的密码题型,需要特意去找相应的解题思路,直接百度搜索天干地支解密即可 3. 一眼能出思路他已经给了篱笆墙的提示提示你是栅栏密码对应解密即可 4. 最简单的社会主…...

Redisson—分布式服务
一、 分布式远程服务(Remote Service) 基于Redis的Java分布式远程服务,可以用来通过共享接口执行存在于另一个Redisson实例里的对象方法。换句话说就是通过Redis实现了Java的远程过程调用(RPC)。分布式远程服务基于可…...
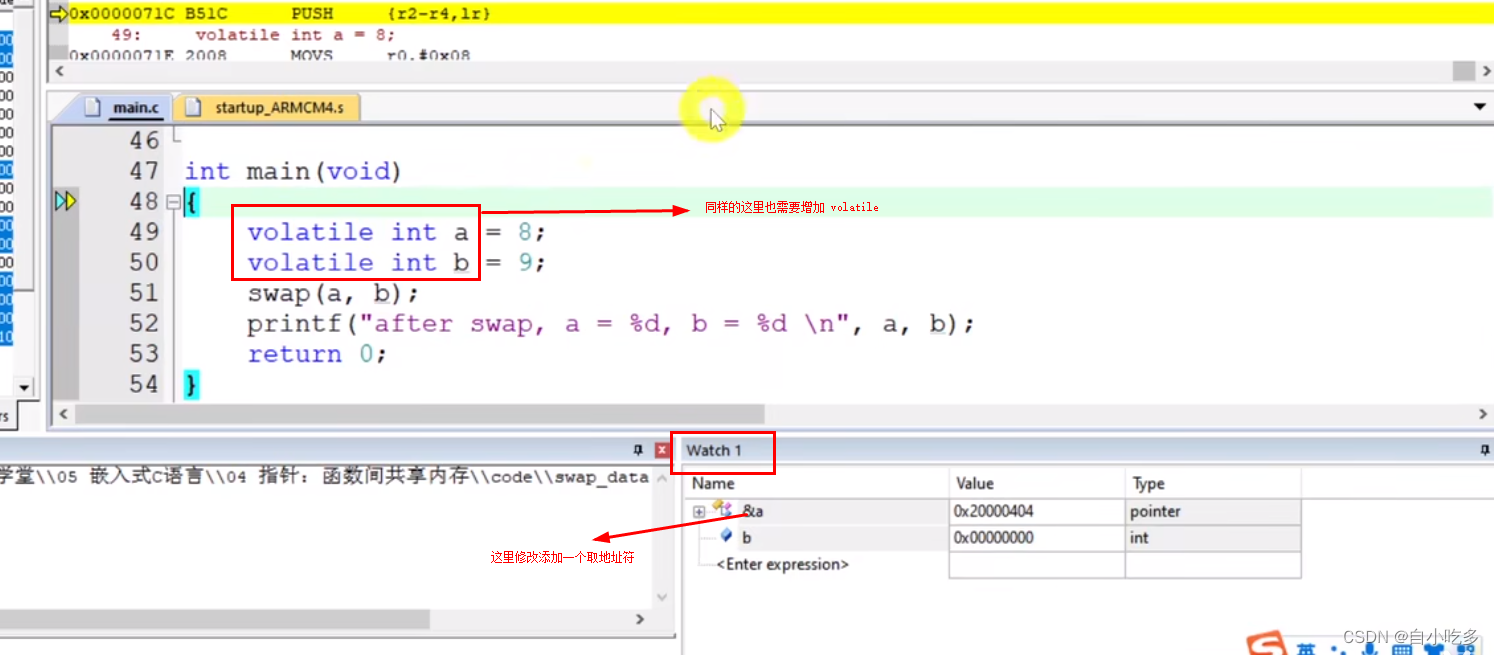
volatile使用方法
volatile使用方法 编译优化。使用等级3的话,可能将优化了一些变量。 这为什么会开启等第三呢?这是关于单片机的内存容量比较小,所以开启优化的话,可以可以省一些空间,但是如果。会出现些变量的问题,需要通过…...

提升您的 Go 应用性能的 6 种方法
优化您的 Go 应用程序 1. 如果您的应用程序在 Kubernetes 中运行,请自动设置 GOMAXPROCS 以匹配 Linux 容器的 CPU 配额 Go 调度器 可以具有与运行设备的核心数量一样多的线程。由于我们的应用程序在 Kubernetes 环境中的节点上运行,当我们的 Go 应用程…...
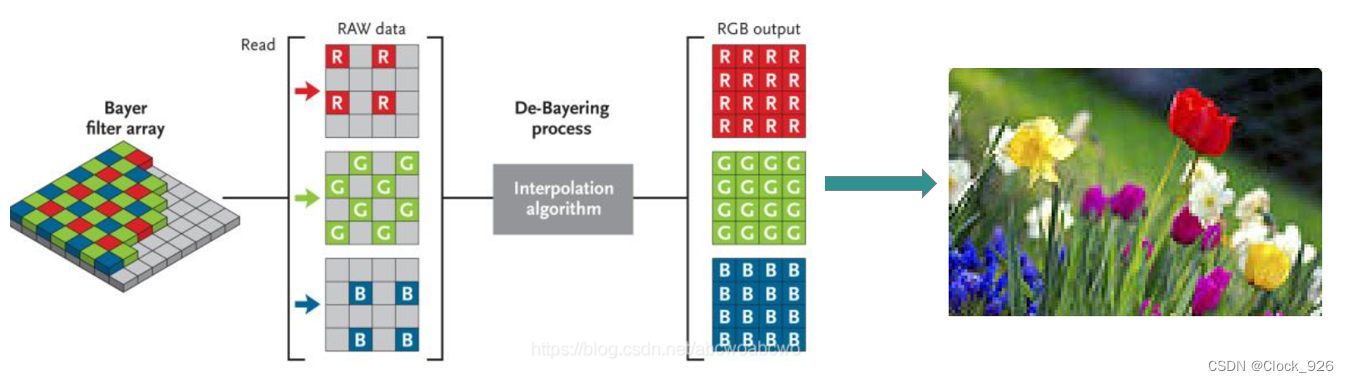
计算摄像技术02 - 颜色空间
一些计算摄像技术知识内容的整理:颜色视觉与感知特性、颜色空间和基于彩色滤镜阵列的彩色感知。 文章目录 一、颜色视觉与感知特性 (1)色调 (2)饱和度 (3)明度 二、颜色空间 (1&…...
Pytorch笔记之分类
文章目录 前言一、导入库二、数据处理三、构建模型四、迭代训练五、模型评估总结 前言 使用Pytorch进行MNIST分类,使用TensorDataset与DataLoader封装、加载本地数据集。 一、导入库 import numpy as np import torch from torch import nn, optim from torch.uti…...
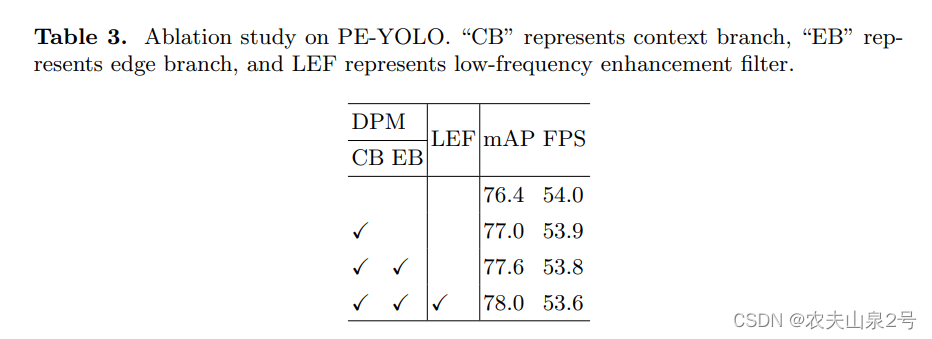
【目标检测】——PE-YOLO精读
yolo,暗光目标检测 论文:PE-YOLO 1. 简介 卷积神经网络(CNNs)在近年来如何推动了物体检测的发展。许多检测器已经被提出,而且在许多基准数据集上的性能正在不断提高。然而,大多数现有的检测器都是在正常条…...

Java 数组转集合
数组转集合 如果仅仅这样转化Arrays.asList(数组),导致集合只能查询,无法进行其他操作,因此,对该方法进行优化: List<实体> list1 new ArrayList<>(Arrays.asList(数组))以上方法就可以使用集合的所有操…...
Elasticsearch:ES|QL 查询语言简介
警告:此功能处于技术预览阶段,可能会在未来版本中更改或删除。 Elastic 将尽最大努力解决任何问题,但技术预览版中的功能不受官方 GA 功能的支持 SLA 的约束。在目前的 Elastic Stack 8.10 中此功能还没有提供。 Elasticsearch 查询语言 (ES|…...

qt qml中listview出现卡顿情况时的常用处理方法
如果在qt QML中使用ListView时出现卡顿情况,可能是因为渲染大量的数据或者在模型中进行复杂的数据处理。以下是常用的解决方法: 1. 设置ListView的缓存策略:通过设置ListView的cacheBuffer属性为适当的值,可以提高滚动的流畅性。…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

什么是VR全景技术
VR全景技术,全称为虚拟现实全景技术,是通过计算机图像模拟生成三维空间中的虚拟世界,使用户能够在该虚拟世界中进行全方位、无死角的观察和交互的技术。VR全景技术模拟人在真实空间中的视觉体验,结合图文、3D、音视频等多媒体元素…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

StarRocks 全面向量化执行引擎深度解析
StarRocks 全面向量化执行引擎深度解析 StarRocks 的向量化执行引擎是其高性能的核心设计,相比传统行式处理引擎(如MySQL),性能可提升 5-10倍。以下是分层拆解: 1. 向量化 vs 传统行式处理 维度行式处理向量化处理数…...
