力扣第101题 c++ 递归 迭代 双方法 +注释 ~
题目
101. 对称二叉树
简单
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
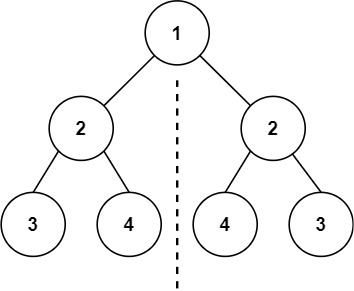
输入:root = [1,2,2,3,4,4,3] 输出:true
示例 2:
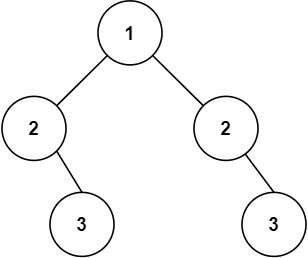
输入:root = [1,2,2,null,3,null,3] 输出:false
提示:
- 树中节点数目在范围
[1, 1000]内 -100 <= Node.val <= 100
进阶:你可以运用递归和迭代两种方法解决这个问题吗?
思路和解题方法一(递归)
compare()函数是用来判断两个节点是否对称的,其中left和right参数分别代表左右子节点。首先我们需要判断
left和right是否为空,若其中一个节点为空而另一个不为空,那么这两个节点不对称,返回false。如果两个节点都为空,则认为它们对称,返回true。如果两个节点的值不相等,则说明它们不对称,返回
false。如果两个节点的值相等,则需要递归判断它们的左右子节点是否对称。具体来说,需要比较左子树的左子节点和右子树的右子节点、左子树的右子节点和右子树的左子节点是否对称,即
outside = compare(left->left, right->right)和inside = compare(left->right, right->left)。最后,给出判断结果,即只有当左子树的左子节点和右子树的右子节点、左子树的右子节点和右子树的左子节点都对称时,才可以认为这两个节点对称,返回
isSame = outside && inside。
isSymmetric()函数是判断整个二叉树是否对称的。如果给定的根节点root为空,则直接返回true。否则,调用compare()函数比较根节点的左右子节点是否对称。最后,整个程序返回的是
isSymmetric()函数的返回值。
复杂度
时间复杂度:
O(n)
时间复杂度是O(n),其中n为二叉树的节点数,因为我们需要遍历每个节点,每个节点都需要进行一次比较。
空间复杂度
O(n)
空间复杂度也是O(n),因为在递归调用
compare()函数时,需要不断开辟新的栈空间来存储递归函数的参数和局部变量,最坏的情况下需要递归到最深层,此时栈空间的大小为O(n)。
c++ 代码
//复杂简单版
class Solution {
public:// 判断节点是否对称的函数bool compare(TreeNode* left, TreeNode* right) {// 首先排除空节点的情况if (left == NULL && right != NULL) return false;else if (left != NULL && right == NULL) return false;else if (left == NULL && right == NULL) return true;// 排除了空节点,再排除数值不相同的情况else if (left->val != right->val) return false;// 此时就是:左右节点都不为空,且数值相同的情况// 此时才做递归,做下一层的判断bool outside = compare(left->left, right->right); // 左子树:左、 右子树:右bool inside = compare(left->right, right->left); // 左子树:右、 右子树:左bool isSame = outside && inside; // 左子树:中、 右子树:中 (逻辑处理)return isSame;}// 判断整棵二叉树是否对称的函数bool isSymmetric(TreeNode* root) {if (root == NULL) return true;// 如果根节点不为空,调用compare()函数比较左子节点和右子节点是否对称return compare(root->left, root->right);}
};//精简版
class Solution {
public:// 检查两个节点是否对称的函数bool check(TreeNode *p, TreeNode *q) {// 如果两个节点都为空,视为对称if (!p && !q) return true;// 如果其中一个节点为空,另一个节点非空,视为不对称if (!p || !q) return false;// 检查当前节点的值是否相等,并递归检查左子树和右子树是否对称return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);}// 判断整棵二叉树是否对称的函数bool isSymmetric(TreeNode* root) {// 调用check函数,同时传入相同的根节点,判断左子树和右子树是否对称return check(root, root);}
};
思路和解题方法二(迭代)
首先检查根节点是否为空,若为空直接返回true。
创建一个队列que,并将根节点的左子树和右子树头结点依次加入队列。
进入while循环,判断队列是否为空。如果队列不为空,则继续执行循环体。
在循环体中,从队列中取出两个节点:leftNode为队列首部的节点,rightNode为队列次首部的节点。
判断左节点和右节点是否都为空。如果是,说明当前节点属于对称的部分,继续循环。
如果左节点和右节点有一个为空,或者它们的值不相等,返回false,表示不对称。
如果左节点和右节点都不为空且值相等,将其左孩子、右孩子按顺序依次加入队列,以备后续判断是否对称。
循环结束后,返回true,表示二叉树是对称的。
复杂度
时间复杂度:
O(n)
时间复杂度为O(n),其中n是二叉树的节点数。
空间复杂度
O(n)
使用了一个队列来存储节点,因此,空间复杂度为O(n)。
c++ 代码
class Solution {
public:bool isSymmetric(TreeNode* root) { // 判断二叉树是否对称的函数,传入根节点rootif (root == NULL) return true; // 如果根节点为空,返回truequeue<TreeNode*> que; // 创建一个队列que来存储需要判断的节点que.push(root->left); // 将左子树头结点加入队列que.push(root->right); // 将右子树头结点加入队列while (!que.empty()) { // 当队列不为空时,进行循环TreeNode* leftNode = que.front(); que.pop(); // 取出队列首部的节点leftNodeTreeNode* rightNode = que.front(); que.pop(); // 取出队列次首部的节点rightNodeif (!leftNode && !rightNode) { // 如果左节点为空、右节点为空,说明是对称的,继续循环continue;}// 左右一个节点不为空,或者都不为空但数值不相同,返回falseif ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {return false; // 如果左右节点有一个为空或者值不相等,直接返回false,表示当前二叉树不对称}// 加入左节点左孩子、右节点右孩子、左节点右孩子、右节点左孩子que.push(leftNode->left); // 左节点的左孩子que.push(rightNode->right); // 右节点的右孩子que.push(leftNode->right); // 左节点的右孩子que.push(rightNode->left); // 右节点的左孩子}return true; // 当循环结束时,说明整个二叉树都对称,返回true}
};
觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。
每天都会不定时更新哦 >人< 。
相关文章:

力扣第101题 c++ 递归 迭代 双方法 +注释 ~
题目 101. 对称二叉树 简单 给你一个二叉树的根节点 root , 检查它是否轴对称。 示例 1: 输入:root [1,2,2,3,4,4,3] 输出:true示例 2: 输入:root [1,2,2,null,3,null,3] 输出:false提示&a…...
Go:实现SMTP邮件发送订阅功能(包含163邮箱、163企业邮箱、谷歌gmail邮箱)
需求很简单,就是用户输入自己的邮箱后,使用官方邮箱给用户发送替邮件模版 目录 前置邮件模版邮箱开启SMTP服务163邮箱163企业邮箱谷歌gmail邮箱腾讯企业邮箱-失败其他邮箱-未操作 邮件发送核心代码config.yaml配置读取邮件相关配置发送邮件 附录 前置 邮…...
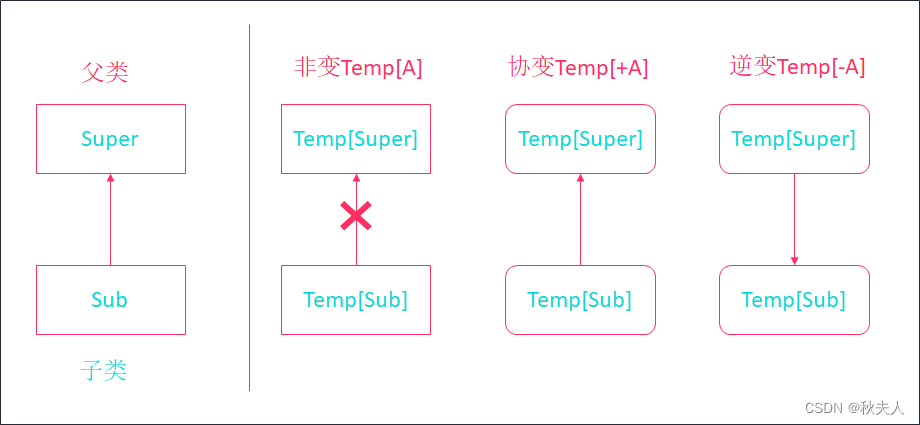
Scala第十六章节
Scala第十六章节 scala总目录 文档资料下载 章节目标 掌握泛型方法, 类, 特质的用法了解泛型上下界相关内容了解协变, 逆变, 非变的用法掌握列表去重排序案例 1. 泛型 泛型的意思是泛指某种具体的数据类型, 在Scala中, 泛型用[数据类型]表示. 在实际开发中, 泛型一般是结合…...

C语言 实现 链 显示 效果 查找 修改 删除
显示所有信息 2023年10月1日的描述:今天放假 2023年10月2日的描述:今天有体育 2023年10月3日的描述:今天有数学 2023年10月4日的描述:今天有语文 2023年10月5日的描述:今天有政治 2023年10月6日的描述:今天交学费 2023年10月7日的描述:今天周末 2023年10月8日的描述:今天给家里…...

CSS基础语法第一天
目录 一、CSS 简介 1.1 CSS简介 1.2 CSS语法 1.3 CSS 语法规范 1.4 CSS 代码风格 1.4.1 样式格式书写 1.4.2 样式大小写 1.4.3 空格规范 二、CSS 基础选择器 2.1选择器分类 2.2标签选择器 2.3 类选择器 2.4 id选择器 2.5 通配符选择器 三、盒子尺寸和背景色 …...

Leetcode 1492.n的第k个因子
给你两个正整数 n 和 k 。 如果正整数 i 满足 n % i 0 ,那么我们就说正整数 i 是整数 n 的因子。 考虑整数 n 的所有因子,将它们 升序排列 。请你返回第 k 个因子。如果 n 的因子数少于 k ,请你返回 -1 。 示例 1: 输入&#…...
十一工具箱流量主小程序源码
无授权,去过滤机制版本 看到网上发布的都是要授权的 朋友叫我把他去授权,能用就行 就把过滤去了 这样就不用授权 可以免费使用 白嫖党专属 一切接口可用,无需担心不能用 授权者不关站一直可以用 源码下载:https://download.csdn.…...
10.5汇编语言整理
【汇编语言相关语法】 1.汇编语言的组成部分 1.伪操作:不参与程序的执行,但是用于告诉编译器程序该怎么编译 .text .global .end .if .else .endif .data 2.汇编指令 编译器将一条汇编指令编译成一条机器码,在内存里一条指令占4字节内存&…...

Connect to 127.0.0.1:1080 [/127.0.0.1] failed: Connection refused: connect
报错信息 A problem occurred configuring root project CourseSelection. > Could not resolve all artifacts for configuration :classpath.> Could not resolve com.android.tools.build:gradle:3.6.1.Required by:project :> Could not resolve com.android.tool…...
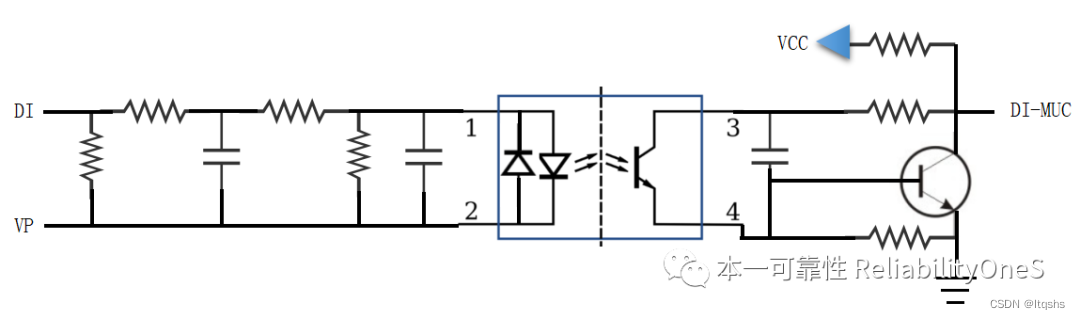
驱动器类产品的接口EMC拓扑方案
驱动器类产品的接口EMC拓扑方案 1. 概述 本文以高压伺服驱动器和变频器类产品为例,对常用端口滤波拓扑方案进行总结,后续根据不同的应用场景可进行适当删减,希望对大家有帮助。 2. 驱动器验证等级 本文推荐拓扑的实验结果,满足…...
2023最新ICP备案查询系统源码 附教程 Thinkphp框架
2023最新ICP备案查询系统源码 附教程 thinkphp框架 本系统支持网址备案,小程序备案,APP备案查询,快应用备案查询 优势: 响应速度快,没有延迟,没有缓存,数据与官方同步 源码下载:ht…...

大数据Doris(六):编译 Doris遇到的问题
文章目录 编译 Doris遇到的问题 一、js_generator.cc:(.text+0xfc3c): undefined reference to `well_known_types_js’...
vue重修004上部
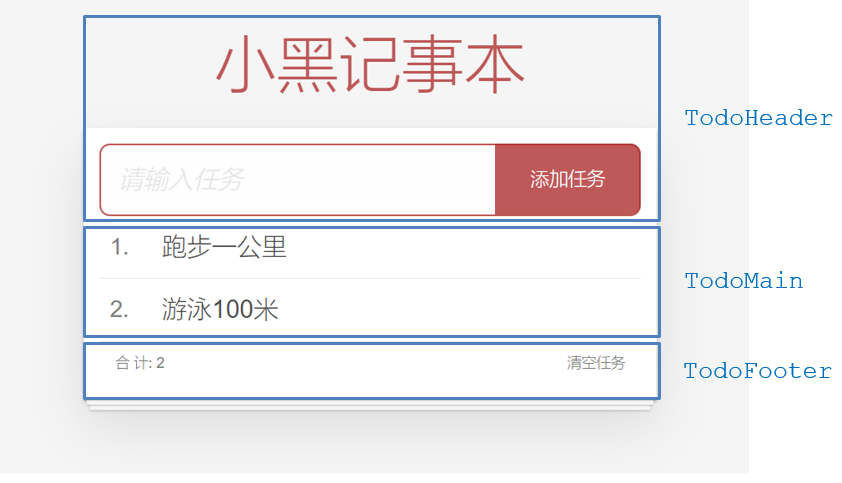
文章目录 版权声明组件的三大组成部分scoped解决样式冲突scoped原理2.代码演示 组件data函数说明演示 组件通信组件关系分类通信解决方案父子通信流程子向父通信代 props详解props校验props&data、单向数据流 小黑记事本(组件版)基础组件结构需求和实…...

【C++ techniques】要求/禁止/判断—对象产生于堆中
有时候我们想让某种对象具有“自杀”的能力,所以我们必须要求对象存在堆中,以便我们调用delete this;另一些时候,我们要求拥有某种确定性,保证某一些类型绝不会发生内存泄漏,原因是没有任何一个该类型的对象…...

吃鸡高手亲授:玩转绝地求生,分享顶级游戏干货!
绝地求生(PUBG)自上线以来,成为了全球热门游戏。作为吃鸡行家,我将分享一些独家技巧和干货,帮助您提高游戏战斗力,享受顶级游戏作战体验! 首先,让我们谈一谈战斗力升级。想要在吃鸡游…...

Vue中如何进行自定义图表与可视化图形设计
Vue中如何进行自定义图表与可视化图形设计 在现代Web应用程序开发中,数据可视化图表和图形设计是至关重要的一部分。Vue.js是一个流行的JavaScript框架,它提供了强大的工具来构建交互性强大的用户界面。本文将探讨如何在Vue.js中进行自定义图表和可视化…...
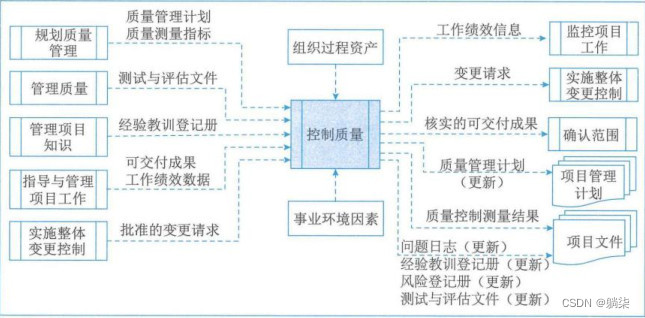
学信息系统项目管理师第4版系列19_质量管理
1. 公差 1.1. 质量测量中公差是测量指标的可允许变动范围,而不是实际测量值与预期值的差 1.1.1. 【高22下选35】 1.2. 结果的的可接受范围 2. 控制界限 2.1. 统计意义上稳定的过程或过程绩效的普通偏差的边界 3. 3版 3.1. 质量控制新七工具 3.1.1. 【高19下…...

react库的基础学习
React介绍 React.js是前端三大新框架:Angular.js、React.js、Vue.js之一,这三大新框架的很多理念是相同的,但是也有各自的特点。 React起源于Facebook的内部项目,因为该公司对市场上所有 JavaScript MVC 框架,都不满…...
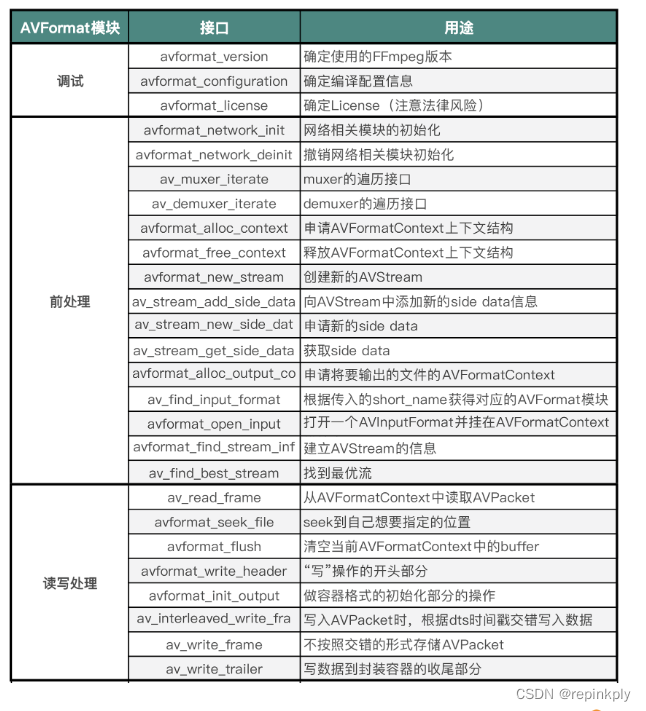
FFmpeg 基础模块:容器相关的 API 操作
目录 AVFormat 模块 AVFormat 前处理部分 AVFormat 读写处理部分 小结 思考 FFmpeg 目录中包含了 FFmpeg 库代码目录、构建工程目录、自测子系统目录等,具体内容如下: 现在你知道 FFmpeg 的源代码目录中都包含了哪些内容,在之后使用 FFm…...
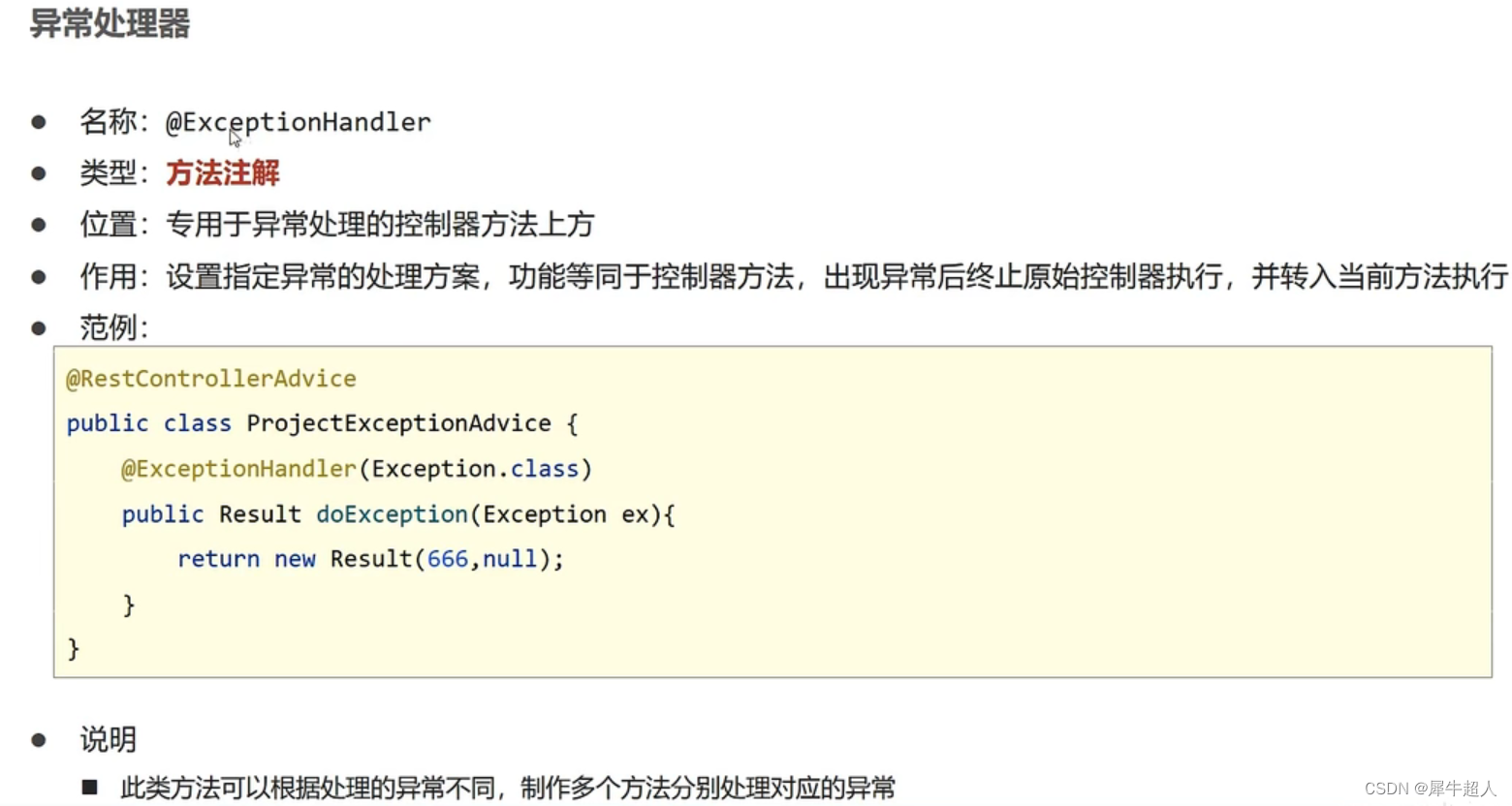
SpringMVC+统一表现层返回值+异常处理器
一、统一表现层返回值 根据我们不同的处理方法,返回的数据格式都会不同,例如添加只返回true|false,删除同理,而查询却返回数据。 Result类 为此我们封装一个result类来用于表现层的返回。 public class Result {//描述统一格式…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
