【数据结构-二叉树 九】【树的子结构】:树的子结构
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【子结构】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为:目标公司+最近一年+出现频率排序,由高到低的去牛客TOP101去找,只有两个地方都出现过才做这道题(CodeTop本身汇聚了LeetCode的来源),确保刷的题都是高频要面试考的题。
明确目标题后,附上题目链接,后期可以依据解题思路反复快速练习,题目按照题干的基本数据结构分类,且每个分类的第一篇必定是对基础数据结构的介绍。
树的子结构【MID】
双重递归,前所未有的体验
题干
直接粘题干和用例

解题思路
原题解地址,若树 B 是树 A 的子结构,则子结构的根节点可能为树 A 的任意一个节点。因此,判断树 B 是否是树 A 的子结构,需完成以下两步工作:
- 先序遍历树 A 中的每个节点 node ;(对应函数
isSubStructure(A, B)) - 判断树 A 中以 node 为根节点的子树是否包含树 B 。(
对应函数 recur(A, B))
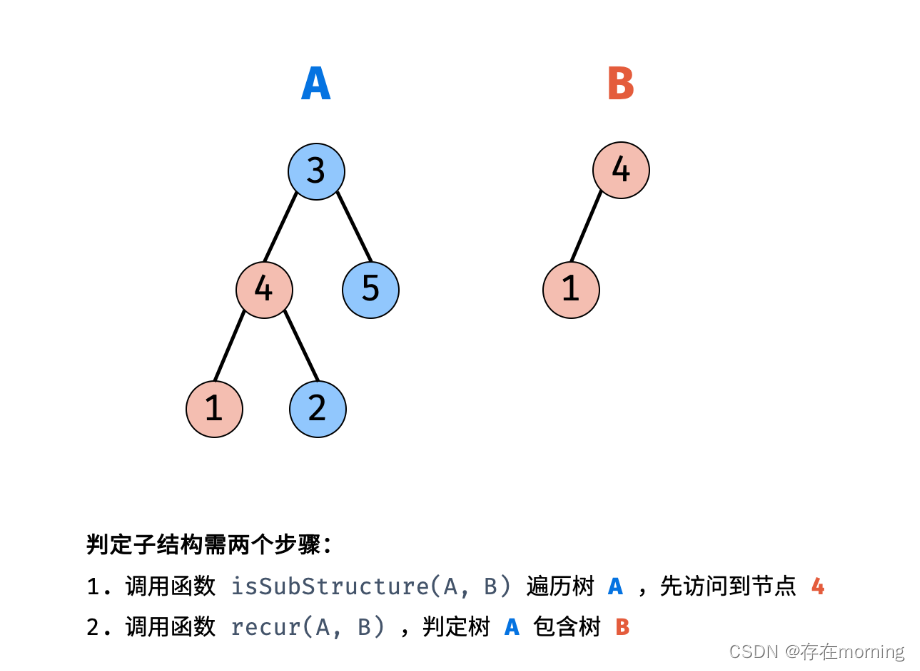
树 A 的根节点记作 节点 A ,树 B 的根节点称为 节点 B 。
recur(A, B) 函数:
终止条件:
- 当节点 B 为空:说明树 B 已匹配完成(越过叶子节点),因此返回 true ;
- 当节点 A 为空:说明已经越过树 A 的叶节点,即匹配失败,返回 false;
- 当节点 A 和 B 的值不同:说明匹配失败,返回 false ;
返回值:
- 判断 A 和 B 的 左子节点 是否相等,即
recur(A.left, B.left); - 判断 A 和 B 的 右子节点 是否相等,即
recur(A.right, B.right);
isSubStructure(A, B) 函数:
特例处理: 当 树 A 为空 或 树 B 为空 时,直接返回 false;
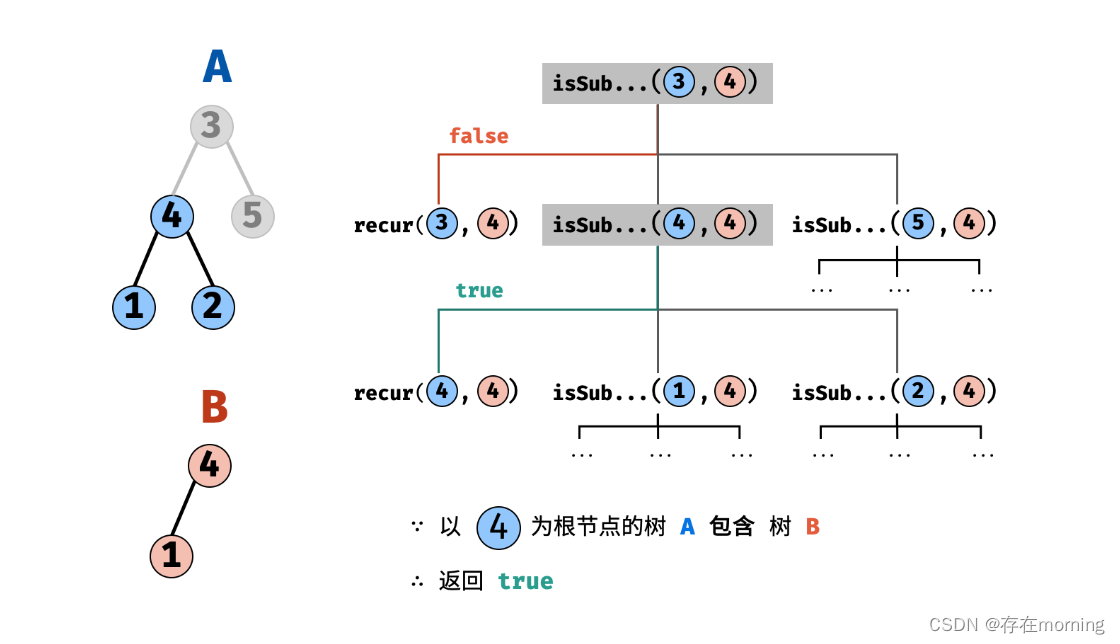
返回值: 若树 B 是树 A 的子结构,则必满足以下三种情况之一,因此用或 || 连接;
- 以 节点 A 为根节点的子树 包含树 B ,对应 recur(A, B);
- 树 B 是 树 A 左子树 的子结构,对应
isSubStructure(A.left, B); - 树 B 是 树 A 右子树 的子结构,对应
isSubStructure(A.right, B);
代码实现
给出代码实现基本档案
基本数据结构:二叉树
辅助数据结构:无
算法:递归
技巧:无
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
当然包括但不限于以上
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode(int x) { val = x; }* }*/
class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param n int整型 the n* @return int整型*/public boolean isSubStructure(TreeNode A, TreeNode B) {// 1 如果A树或B树为空,则匹配失败if (A == null || B == null) {return false;}// 2 A的当前节点包含B,或A的左子树包含B,或A的右子树包含Breturn isNodeSub(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);}private boolean isNodeSub(TreeNode node, TreeNode B) {// 1 如果B为空,说明B节点比对完成,匹配成功【终止条件】if (B == null ) {return true;}// 2 如果B不为null,且node为空,说明尚未匹配完B但已越过A的节点树叶子节点,匹配失败【终止条件】if (node == null ) {return false;}// 3 如果node节点值不等于B,则说明不是子结构,匹配失败【本层任务】if (node.val != B.val) {return false;}// 4 比较node与B的左右子节点,必须都满足条件才可以【返回值】return isNodeSub(node.left, B.left) && isNodeSub(node.right, B.right);}
}
复杂度分析
- 时间复杂度 O(MN): 其中 M,N分别为树 A 和 树 B 的节点数量;先序遍历树 A 占用 O(M) ,每次调用
recur(A, B)判断占用 O(N)。 - 空间复杂度 O(M) : 当树 A 和树 B 都退化为链表时,递归调用的深度取决于二叉树A的高度,最坏情况下,二叉树A是一个完全不平衡的树,高度为M,因此递归调用的最大深度为M。每次递归调用都需要一些额外的栈空间来保存函数调用的上下文,因此空间复杂度为O(M)
相关文章:

【数据结构-二叉树 九】【树的子结构】:树的子结构
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【子结构】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&…...

七张图解锁Mybatis整体脉络,让你轻松拿捏面试官
前言 MyBatis是一款ORM(Object-Relational Mapping)框架,其主要用于将Java对象与关系数据库之间进行映射,凭借其轻量性、稳定性以及广泛的开源社区其受到了广大开发者的追捧。 那MyBatis为我们做了哪些事情呢?其实&a…...

力扣之删除有序数组中的重复项
力扣:26. 删除有序数组中的重复项 - 力扣(LeetCode) 方法:双指针法。 我的方法: class Solution { public:int removeDuplicates(vector<int>& nums) {int slow 0,fast;for(fast 0; fast < nums.size()…...

pnpm、npm、yarn 包管理工具『优劣对比』及『环境迁移』
前言 博主在开发前端网站的时候,发现随着开发的项目的逐渐增多,安装的依赖包越来越臃肿,依赖包的安装速度也是非常越来越慢,多项目开发管理也是比较麻烦。之前我就了解过 pnpm,但是当时担心更换包管理环境可能会出现的…...
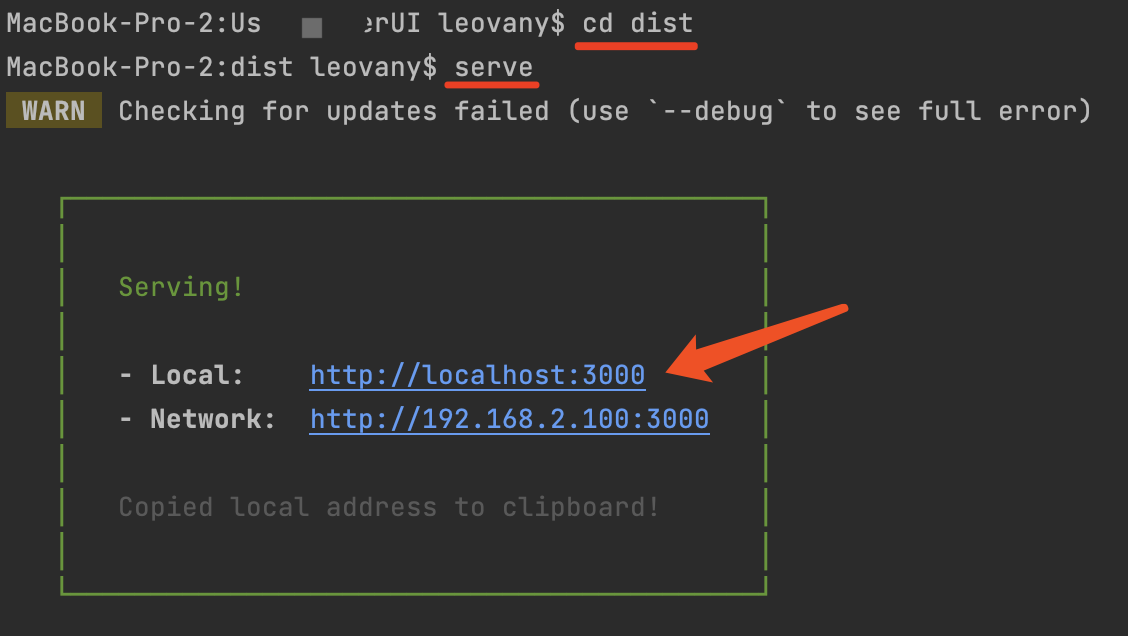
【AntDesign】多环境配置和启动
环境分类,可以分为 本地环境、测试环境、生产环境等,通过对不同环境配置内容,来实现对不同环境做不同的事情。 AntDesign 项目,通过 config.xxx.ts 添加不同的后缀来区分配置文件,启动时候通过后缀启动即可。 config…...

Unix Network Programming Episode 78
‘getaddrinfo’ Function The gethostbyname and gethostbyaddr functions only support IPv4. The API for resolving IPv6 addresses went through several iterations, as will be described in Section 11.20(See 8.9.20); the final result is the getaddrinfo function…...
学习笔记(css穿透、vue-cookie、拦截器、vuex、导航守卫、token/Cookie、正则校验)
目录 一、记录 1、CSS穿透 2、输入框是否提示输入 3、插槽 #slot 4、v-deep深入改掉属性值 二、vue-cookie 1、官方文档 2、使用 三、拦截器 1、请求拦截器 2、响应拦截器 四、vuex对信息存取改 五、路由导航守卫 1、登录思路 2、设置白名单 六、Token与Cookie…...
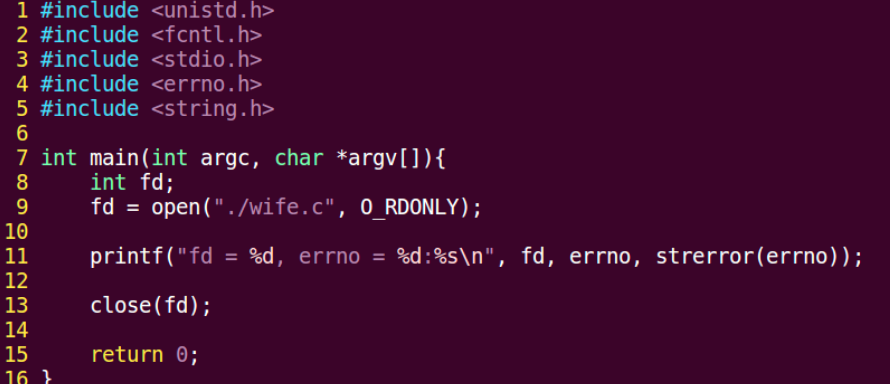
Day4:Linux系统编程1-60P
我的学习方法是:Linux系统编程(看pdf笔记) Linux网络编程 WebServer 01P-17P Linux相关命令及操作 cp -a dirname1 dirname2 复制目录 cp -r dirname1 dirname2 递归复制目录 1 到目录 2 这里-a 和-r 的差别在于,-a 是完全复制…...
支持的模型)
【HuggingFace】Transformers(V4.34.0 稳定)支持的模型
Transformer 4.43.40 版本是自然语言处理领域的一个重要工具包,为开发者提供了丰富的预训练模型资源,可以用于各种文本处理任务。在这个版本中,Transformer 支持了众多模型,每个模型都具有不同的优势和适用领域。下面是一个 Trans…...

oracle 导入数据泵常用语句
oracle常用语句 window10 导出导入数据泵文件导入数据泵文件导出数据泵文件 oracle表空间查询、剩余空间查询查询表空间大小及对应文件查询各个表空间大小扩充表空间 window10 导出导入数据泵文件 导入数据泵文件 首先将数据泵文件放在oracle安装得对应位置,例如&…...

tensorflow中的常见方法
1.tf.argmax(input,axis) tf.argmax(input,axis)根据axis取值的不同返回每行或者每列最大值的索引。 axis 0: 比较每一列的元素,将每一列最大元素所在的索引记录下来,最后输出每一列最大元素所在的索引数组。 test[0] array([1, 2, 3]) test[1] …...
【周末闲谈】“PHP是最好的语言”这个梗是怎么来的?
个人主页:【😊个人主页】 系列专栏:【❤️周末闲谈】 系列目录 ✨第一周 二进制VS三进制 ✨第二周 文心一言,模仿还是超越? ✨第二周 畅想AR 文章目录 系列目录前言最早的出处关于PHP语言优点缺点网络评价 总结 前言 …...

四位十进制数字频率计VHDL,仿真视频、代码
名称:四位十进制数字频率计VHDL,quartus仿真 软件:Quartus 语言:VHDL 代码功能: 使用直接测频法测量信号频率,测频范围为1~9999Hz,具有超量程报警功能 演示视频:四位十进制数字频…...
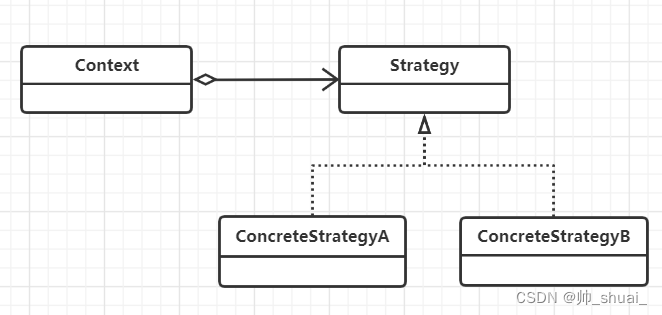
Unity实现设计模式——策略模式
Unity实现设计模式——策略模式 策略模式是一种定义一些列算法的方法,这些所有的算法都是完成相同的工作,只是实现不同。它可以通过相同的方式调用所有的算法,减少各种算法类与使用算法类之间的耦合。 策略模式的 Strategy 类层次为 Contex…...

C++基础——数据类型
1 概述 在创建变量和常量的时候,都需要指定其数据类型,以便为其分配合适的内存空间。 其中宏常量不需要指定类型,是因为宏定义是字符替换。 2 整型 整型表示的是整数,C中的整型有以下几种: 数据类型占用空间取值范…...

文本自动输入/删除的加载动画效果
效果展示 CSS 知识点 绕矩形四周跑的光柱动画实现animation 属性的 steps 属性值运用 页面基础结构实现 <div class"loader"><!-- span 标签是围绕矩形四周的光柱 --><span></span><span></span><span></span>&l…...

PHP8的匿名类-PHP8知识详解
PHP8支持通过new class 来实例化一个匿名类。所谓匿名类,就是指没有名称的类,只能在创建时使用new语句来声明它们。 匿名类是一种没有命名的即时类,可以用于简单的对象封装和实现接口。 以下是PHP 8中匿名类的基本语法示例: $ob…...
WebKit Inside: CSS 样式表的匹配时机
WebKit Inside: CSS 的解析 介绍了 CSS 样式表的解析过程,这篇文章继续介绍 CSS 的匹配时机。 无外部样式表 内部样式表和行内样式表本身就在 HTML 里面,解析 HTML 标签构建 DOM 树时内部样式表和行内样式就会被解析完毕。因此如果 HTML 里面只有内部样式…...

<HarmonyOS第一课>从简单的页面开始——闯关习题及答案
加入鸿蒙应用开发公开课系统学习HarmonyOS应用开发 判断题 1.在Column容器中的子组件默认是按照从上到下的垂直方向布局的,其主轴的方向是垂直方向,在Row容器中的组件默认是按照从左到右的水平方向布局的,其主轴的方向是水平方向。ÿ…...

视频下载plus+:一款强大的视频下载小程序
引言 在当下,随着视频号的火爆和用户数量的不断增加,视频下载已经成为了众多用户追求的目标。尽管市面上有很多视频下载助手,但是很多人对于如何下载视频还是摸不着头脑。今天我将向大家推荐一款我自己使用并且非常好用的视频下载小程序——…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

Mac flutter环境搭建
一、下载flutter sdk 制作 Android 应用 | Flutter 中文文档 - Flutter 中文开发者网站 - Flutter 1、查看mac电脑处理器选择sdk 2、解压 unzip ~/Downloads/flutter_macos_arm64_3.32.2-stable.zip \ -d ~/development/ 3、添加环境变量 命令行打开配置环境变量文件 ope…...
)
Java中Git基础操作详解(clone、commit、push、branch)
Git是Java开发者必备的版本控制工具,以下是核心操作的详细说明及示例: 一、Git基础概念 仓库(Repository):存储代码的目录,包含所有版本历史。提交(Commit)…...
