布隆过滤器的使用
布隆过滤器简介
Bloom Filter(布隆过滤器)是一种多哈希函数映射的快速查找算法。它是一种空间高效的概率型数据结构,通常应用在一些需要快速判断某个元素是否属于集合,但是并不严格要求100%正确的场合。
布隆过滤器的优势在于,利用很少的空间可以做到精确率较高,空间效率和查询时间都比一般的算法要好的多,缺点是有一定的误识别率和删除困难。为什么不允许删除元素呢:删除意味着需要将对应的 k 个 bits 位置设置为 0,其中有可能是其他元素对应的位。
哈希表与布隆过滤器
哈希表也能用于判断元素是否在集合中,但是Bloom Filter只需要哈希表的1/8或1/4的空间复杂度就能完成同样的问题。Bloom Filter可以插入元素,但是不可以删除已有元素。集合中的元素越多,误报率越大,但是不会漏报。
应用场景
布隆过滤器的用处就是,能够在节省存储空间的情况下迅速判断一个元素是否在一个集合中。主要有如下几个典型使用场景:
- 网页爬虫对URL的去重,避免爬取相同的URL地址;
- 反垃圾邮件,从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱;
- 缓存击穿,将已存在的缓存放到布隆过滤器中,当黑客访问不存在的缓存时迅速返回避免缓存及DB挂掉。
- 黑白名单的过滤
原理
如果想判断一个元素是不是在一个集合中,一般想到的方法是暂存数据,然后查找判定是否存在集合中。这种方法在数据量比较小的情况下适用,但是几个中元素较多的时候,检索速度就会越来越慢。
可以利用Bitmap:只要检查对应点是不是1就可以知道集合中有没有这个数。Bloom filter可以看做是对bitmap的扩展。只是使用多个hash映射函数,从而减低hash发生冲突的概率。可以发现由于有hash的介入,布隆过滤器整体上是一种非常概率的数据结构,存在一定的误判率。所以有这样的特性:key命中了布隆过滤器,代表key可能在布隆过滤器中、key没有命中布隆过滤器,代表key一定不在布隆过滤器中。
在Go 中比较常用的是:https://github.com/bits-and-blooms/bloom,我们可以通过分析这个开源的项目来看下布隆过滤器的实现原理
例子
package mainimport ("fmt""github.com/bits-and-blooms/bitset"bloom "github.com/bits-and-blooms/bloom/v3"
)func main() {filter := bloom.NewWithEstimates(1000000, 0.01)filter.Add([]byte("a"))if filter.Test([]byte("a")) {fmt.Println("true")return}fmt.Println("false")
}
数据结构
type BloomFilter struct {m uintk uintb *bitset.BitSet
}// 这个才是 BloomFilter 真正的底层结构,就是一个 []uint64
type BitSet struct {length uintset []uint64
}// 将元素添加到 布隆过滤器 里面
// Add data to the Bloom Filter. Returns the filter (allows chaining)
func (f *BloomFilter) Add(data []byte) *BloomFilter {h := baseHashes(data)for i := uint(0); i < f.k; i++ {f.b.Set(f.location(h, i))}return f
}
可以简单理解成下面这张图,元素1,6,9 经过 hash 函数之后存在了数组中,在Bloom Filters 可视化网站 可以看到动态视频。然后判断存不存在只需要判断hash 之后的元素对应的数组位置是不是都等于1
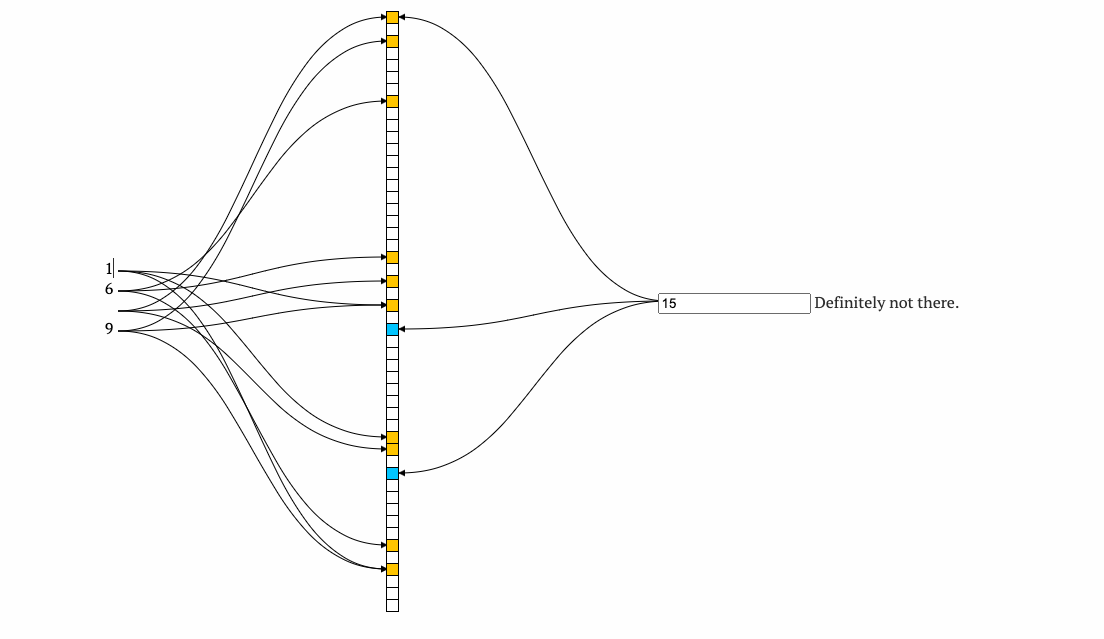
问题
布隆过滤器的容量及误判率该如何设定
- 假设布隆过滤器容量为 n,过滤器误判率为 p, qps 为 x,一次请求对布隆过滤器的访问次数为 g,则极限 qps 场景下每秒对布隆过滤器的访问次数为 xg,那每秒可能会有 xg*p 的请求到 数据源中;假设我们的数据源的请求 qps限制 为 y,那么误判率 p 的估计取值为
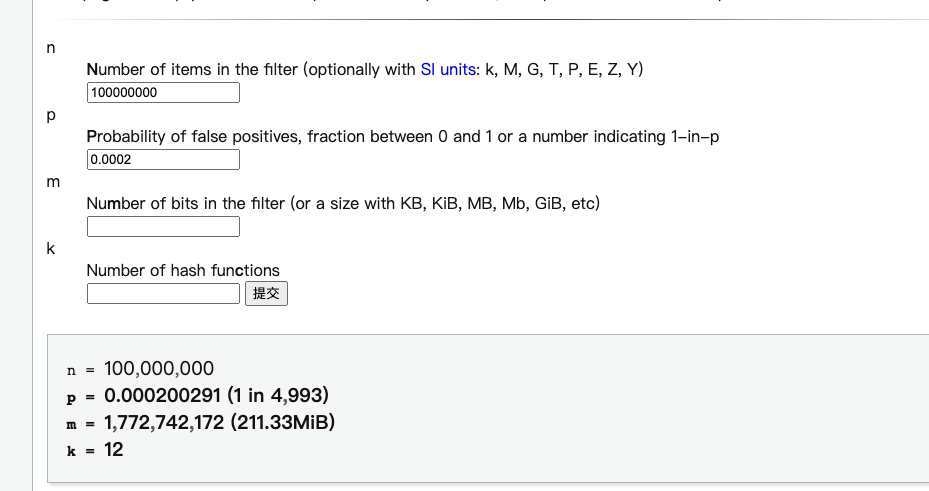
y / (x*g)。 - 知道了容量和误判率之后,我们就可以通过:https://hur.st/bloomfilter/n=100000000&p=0.0002&m=&k= 大致预估出 布隆过滤器 的大小
如何更新布隆过滤器
因为布隆过滤器不能够删除,所以我们只能定时或者手动更新布隆过滤器
布隆过滤器 Redis 大Key问题
在 n= 1 亿,p=0.0002的数据下,布隆过滤器大概在 211.33MiB,这个时候我们存在redis 上,就会造成 redis 大key 问题,有可能会引起redis 的慢查询,拖挂 redis。
我们可以定时生成布隆过滤器讲结果存储在 DB 或者对象存储中,由每一个服务的实例定时去拉取生成的最新布隆过滤器数据。
Redis布隆过滤器
bitmap
在刚刚我们提到,布隆过滤器的核心数据结构为bitmap, 在Redis上也支持bitmap,其实就是对 string 的每一位进行操作。由此我们也可以得出,用 Redis的bitmap实现的布隆过滤器可以存储最大的数据量为:512x1024x1024x8 = 4294967296,42亿。
我们可以通过 SETBIT 来设置 bit的值,GETBIT 来获取 bit位的值
127.0.0.1:6379> SETBIT mykey 7 1
(integer) 0
127.0.0.1:6379> GETBIT mykey 7
(integer) 1
127.0.0.1:6379> SETBIT mykey 7 0
(integer) 1
127.0.0.1:6379> GETBIT mykey 7
(integer) 0
127.0.0.1:6379>
所以通过Redis bitmap来实现布隆过滤器需要做三件事情:
- k 次散列函数计算出 k 个位点。
- 插入时将位数组中 k 个位点的值设置为 1。
- 查询时根据 1 的计算结果判断 k 位点是否全部为 1,否则表示该元素一定不存在
Bloom Filter
我们也可以通过安装 Redis 的插件:https://github.com/RedisBloom/RedisBloom,这个插件包含了很多数据类型。Bloom filter(布隆过滤器), Cuckoo filter(布谷鸟过滤器), Count-min sketch(频率算法), Top-K, t-digest(近似百分位算法)
在Redis中的操作
bloom filter定义
BF.RESERVE {key} {error_rate} {capacity}
使用给定的期望错误率和初始容量创建空的Bloom过滤器(如果不存在的话)。如果打算向Bloom过滤器中添加许多项,则此命令非常有用,否则只能使用BF.ADD 添加项。
初始容量和错误率将决定过滤器的性能和内存使用情况。一般来说,错误率越小(即对误差的容忍度越低),每个过滤器条目的空间消耗就越大。
bloom filter基本操作
BF.ADD {key} {item}
单条添加元素
向Bloom filter添加一个元素,如果该key不存在,则创建该key(过滤器)。
如果项是新插入的,则为“1”;如果项以前可能存在,则为“0”。
BF.MADD {key} {item} [item…]
批量添加元素
布尔数(整数)的数组。返回值为0或1的范围的数据,这取决于是否将相应的输入元素新添加到过滤器中,或者是否已经存在。
BF.EXISTS {key} {item}
判断单个元素是否存在
如果存在,返回1,否则返回0
BF.MEXISTS {key} {item} [item…]
判断多个元素是否存在
其他相关的命令可以在这里查询到:https://redis.io/commands/?name=bf
127.0.0.1:6379> BF.ADD bfKey 1
(integer) 1
127.0.0.1:6379> BF.ADD bfKey foo
(integer) 1
127.0.0.1:6379> BF.EXISTS bfKey 4
(integer) 0
127.0.0.1:6379> BF.EXISTS bfKey 4
(integer) 0
127.0.0.1:6379> BF.EXISTS bfKey 1
(integer) 1
127.0.0.1:6379> BF.EXISTS bfKey foo
(integer) 1
127.0.0.1:6379>
布谷鸟过滤器
为了解决布隆过滤器中不能删除,且存在误判的缺点,本文引入了一种新的哈希算法——cuckoo filter,它既可以确保该元素存在的必然性,又可以在不违背此前提下删除任意元素,仅仅比bitmap牺牲了微量空间效率。
原理
最简单的布谷鸟哈希结构是一维数组结构,会有两个 hash 算法将新来的元素映射到数组的两个位置。如果两个位置中有一个位置为空,那么就可以将元素直接放进去。但是如果这两个位置都满了,它就不得不「鸠占鹊巢」,随机踢走一个,然后自己霸占了这个位置。
- 使用两个哈希函数 h1(x) 、 h2(x) 和两个哈希桶 T1、T2 。
- 插入元素 x:
- 如果 T1[h1(x)] 、T2[h2(x)] 有一个为空,则插入;两者都空,随便选一个插入。
- 如果 T1[h1(x)] 、T2[h2(x)] 都满,则随便选择其中一个(设为 y ),将其踢出,插入 x。
- 重复上述过程,插入元素 y。
- 如果插入时,踢出次数过多,则说明哈希桶满了。则进行扩容、ReHash 后,再次插入。
- 查询元素 x:
- 读取 T1[h1(x)] 、T2[h2(x)] 和 x 比对即可
可以通过这个Cuckoo Filter 可视化网站观察到。
- 读取 T1[h1(x)] 、T2[h2(x)] 和 x 比对即可
其他
- 布谷鸟哈希
- 布谷鸟过滤器
- 布谷鸟过滤器实现
相关文章:

布隆过滤器的使用
布隆过滤器简介 Bloom Filter(布隆过滤器)是一种多哈希函数映射的快速查找算法。它是一种空间高效的概率型数据结构,通常应用在一些需要快速判断某个元素是否属于集合,但是并不严格要求100%正确的场合。 布隆过滤器的优势在于,利用很少的空…...

Web开发-单例模式
目录 单例模式介绍代码实现单例模式 单例模式介绍 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点。单例模式可以通过private属性实现。通过将类的构造函数设为private,可以防止类在外部被实例化。单例模式通…...
MySQL:温备份和恢复-mysqldump (4)
介绍 温备:同样是在数据库运行的时候进行备份的,但对当前数据库的操作会产生影响。(只可以读操作,不可以写操作) 温备份的优点: 1.可在表空间或数据文件级备份,备份时间短。 2.备份时数据库依然…...
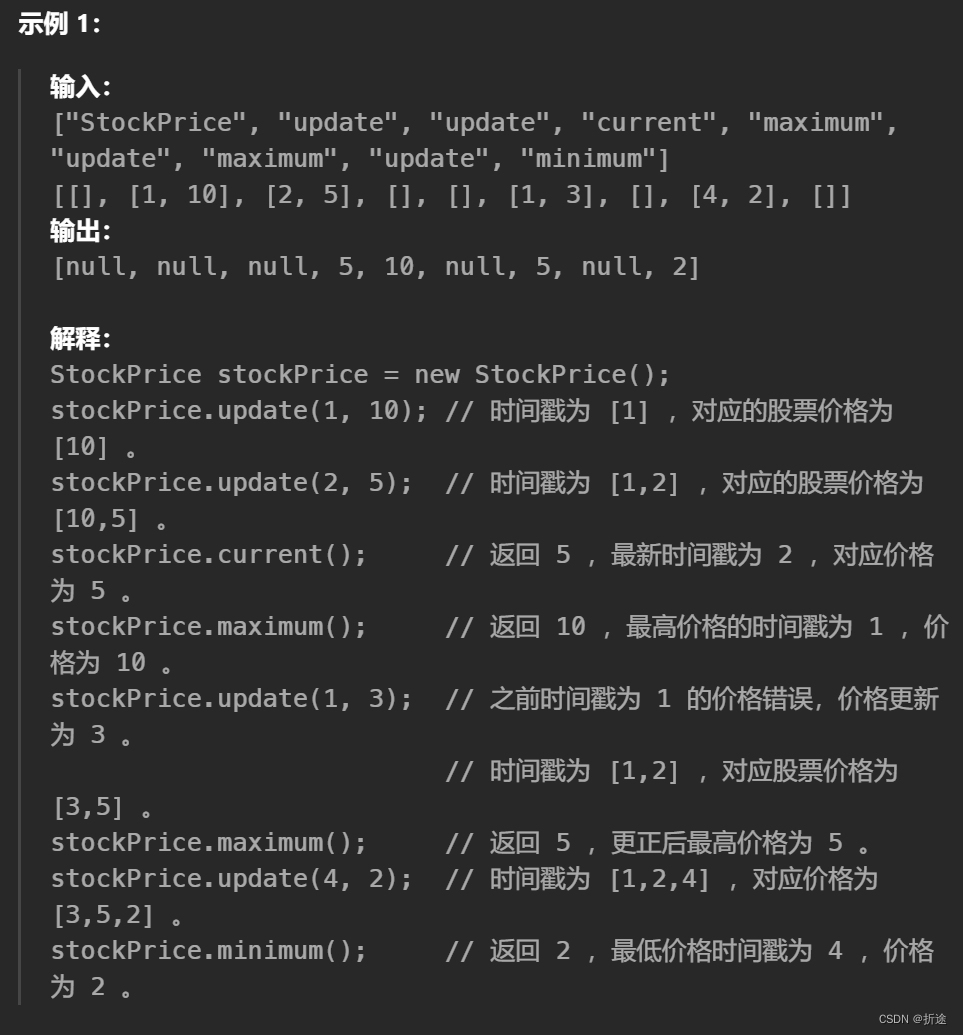
【力扣每日一题】2023.10.8 股票价格波动
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题是程序设计题,要我们实现一个类,一共是四个功能,第一个是给一个时间戳和价格,表示该…...

Linux隐藏文件或文件夹
在Linux中,以点(.)开头的文件或文件夹是隐藏文件或隐藏文件夹。要创建一个隐藏文件或文件夹,可以使用以下命令: 创建隐藏文件: touch .filename这将在当前目录下创建一个名为 “.filename” 的隐藏文件。…...
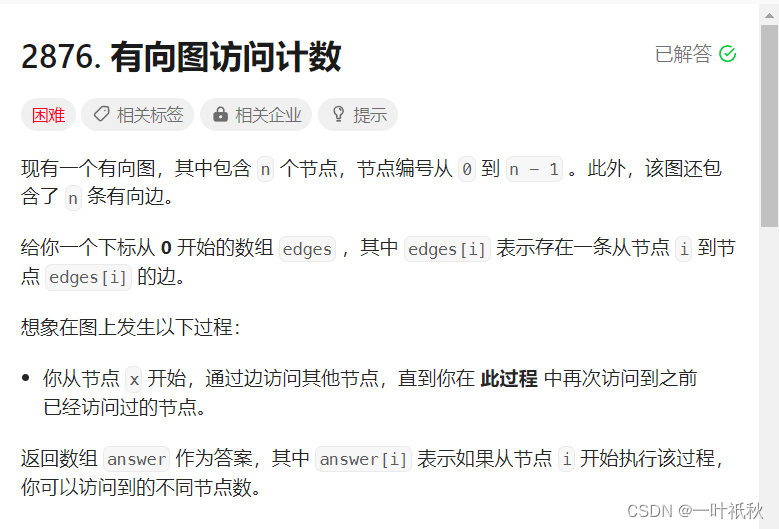
leetcode - 365周赛
一,2873.有序三元组中的最大值 I 该题的数据范围小,直接遍历: class Solution {public long maximumTripletValue(int[] nums) {int n nums.length;long ans 0;for(int i0; i<n-2; i){for(int ji1; j<n-1; j){for(int kj1; k<…...

为什么mac上有的软件删除不掉?
对于Mac用户来说,软件卸载通常是一个相对简单的过程。然而,有时你可能会发现某些软件似乎“顽固不化”,即使按照常规方式尝试卸载,也依然存在于你的电脑上。这到底是为什么呢?本文将探讨这一问题的可能原因。 1.卸载失…...
【vue3】wacth监听,监听ref定义的数据,监听reactive定义的数据,详解踩坑点
假期第二篇,对于基础的知识点,我感觉自己还是很薄弱的。 趁着假期,再去复习一遍 之前已经记录了一篇【vue3基础知识点-computed和watch】 今天在学习的过程中发现,之前记录的这一篇果然是很基础的,很多东西都讲的不够…...
跨境电商如何通过软文建立品牌形象?
在全球产业链结构重塑后的今天,越来越多的企业意识到想要可持续发展,就需要在建立品牌形象,在用户心中留下深刻印象,那么应该如何有效建立品牌形象呢?可以利用软文来打造品牌形象,接下来媒介盒子就告诉大家…...
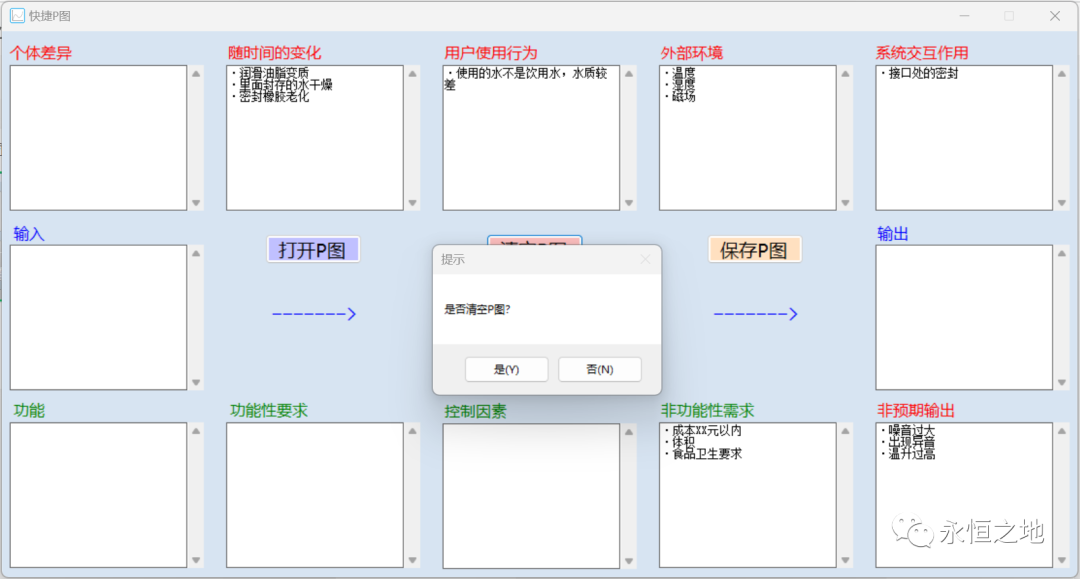
我做了一个简易P图(参数图)分析软件
P图(即参数图,Parameter Diagram),是一个结构化的工具,帮助大家对产品更好地进行分析。 典型P图格式 P图最好是和FMEA软件联动起来,如国可工软的FMEA软件有P图分析这个功能。 单纯的P图分析软件很少,为了方便做P图分…...
:状态,按键分区,算子状态,状态后端。容错机制,检查点,保存点。状态一致性。flink与kafka整合)
209.Flink(四):状态,按键分区,算子状态,状态后端。容错机制,检查点,保存点。状态一致性。flink与kafka整合
一、状态 1.概述 算子任务可以分为有状态、无状态两种。 无状态:filter,map这种,每次都是独立事件有状态:sum这种,每次处理数据需要额外一个状态值来辅助。这个额外的值就叫“状态”2.状态的分类 (1)托管状态(Managed State)和原始状态(Raw State) 托管状态就是由…...
rabbitmq查看节点信息命令失败
不影响访问rabbitmq,但是无法使用 命令查看节点信息 等 查看节点信息命令:rabbitmq-diagnostics status --node rabbitJHComputer Error: unable to perform an operation on node ‘rabbitJHComputer‘. Please see diagnostics informatio rabbitmq-…...
c语言动态内存分布
前言: 随着我们深入的学习c语言,之前使用的静态内存分配已经难以满足我们的实际需求。比如前面我们的通讯录功能的实现,如果只是静态内存分配,那么也就意味着程序开始的内存分配大小就是固定的,应该开多大的空间呢&am…...

1.3.2有理数减法(第一课时)作业设计
【学习目标】 1.理解有理数减法法则,能熟练地进行有理数的减法运算. 2.感受有理数减法与加法对立统一的辨证思想,体会转化的思想方法....
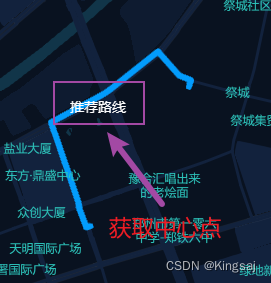
vue3 -- ts封装 Turf.js地图常用方法
Turf.js中文网 地理空间分析库,处理各种地图算法 文档地址 安装 Turf 库 npm install @turf/turf创建src/hooks/useTurf.ts 文件1:获取线中心点 效果: 代码: useTurf.ts import * as turf from @turf/turf// 获取线中心点 export class CenterPointOfLine {...
Qt之实现圆形进度条
在Qt自带的控件中,只有垂直进度条、水平进度条两种。 在平时做页面开发时,有些时候会用到圆形进度条,比如说:下载某个文件的下载进度。 展示效果,如下图所示: 实现这个功能主要由以下几个重点:…...

C# 图解教程 第5版 —— 第1章 C# 和 .NET 框架
文章目录 1.1 在 .NET 之前1.2 .NET 时代1.2.1 .NET 框架的组成1.2.2 大大改进的编程环境 1.3 编译成 CIL1.4 编译成本机代码并执行1.5 CLR1.6 CLI1.7 各种缩写1.8 C# 的演化1.9 C# 和 Windows 的演化(*) 1.1 在 .NET 之前 MFC(Microsoft Fou…...
electronjs入门-聊天应用程序,与Electron.js通信
随着第一章中构建的应用程序,我们将开始将其与Electron框架中的模块集成,并以此为基础,以更实用的方式了解它们。 过程之间的通信 根据第二章中的解释,我们将发送每个进程之间的消息;具体来说联系人和聊天࿱…...
【自用】ubuntu 18.04 LTS安装opencv 3.4.16 + opencv_contrib 3.4.16
1.下载 opencv 3.4.16 opencv_contrib 3.4.16 其中,opencv_contrib解压后的多个文件夹复制到opencv内、合并 声明:尚未验证该方式是否可行 2.安装 参考博文: https://zhuanlan.zhihu.com/p/650792342 https://zhuanlan.zhihu.com/p/8719780…...
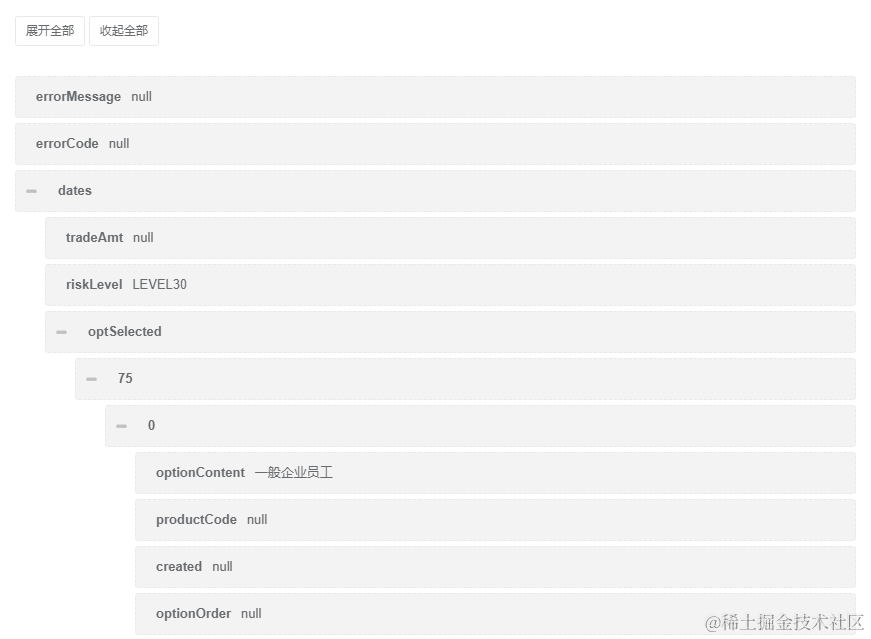
递归解析Json,实现生成可视化Tree+快速获取JsonPath | 京东云技术团队
内部平台的一个小功能点的实现过程,分享给大家: 递归解析Json,可以实现生成可视化Tree快速获取JsonPath。 步骤: 1.利用JsonPath读取根,获取JsonObject 2.递归层次遍历JsonObjec,保存结点信息 3.利用z…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...
