golang的切片使用总结二
如果没看golang切片的第一篇总结博客 golang的切片使用总结一-CSDN博客 ,请浏览之
举例9:make([]int, a, b)后访问下标a的元素
s := make([]int, 10, 12)
v := s[10]
fmt.Printf("v:%v", v)
打印结果:
panic: runtime error: index out of range [10] with length 10
goroutine 1 [running]:
main.main()
结论:capacity(容量)是物理意义上的,空间归切片s所有;但len(长度)是逻辑意义上的,访问元素时是根据逻辑意义为准,因为s[10]认为是越界访问
举例10:make([]int, a, b)后截取新切片,再对新切片append
s := make([]int, 10, 12)
s1 := s[8:]
s1 = append(s1, []int{10, 11, 12}...)
v := s[10]
fmt.Printf("v:%v", v)
打印结果:
panic: runtime error: index out of range [10] with length 10
goroutine 1 [running]:
main.main()
结论:虽然s1从s截取得到,二者共享同一块内存数据。但是后面的s1 = append(s1)操作会让s1发生扩容,s1扩容后就跟s完全分开了,内存完全独立。所以,s还是原来的len为10,访问s[10]会发生panic
举例11:切片在函数中是值传递还是引用传递
func main() {
s := make([]int, 10, 12)
s1 := s[8:]
changeSlice(s1)
fmt.Printf("s: %v", s)
}func changeSlice(s1 []int) {
s1[0] = -1
}
打印结果:s: [0 0 0 0 0 0 0 0 -1 0]
结论:切片s1是从切片s截取得到,传入函数后,由于切片是引用传递,函数内的s1[0]和函数外的s[8]是同一个元素,所以原切片s会被修改
举例12:切片传递到函数内后进行修改,且append
func main() {
s := make([]int, 10, 12)
s1 := s[8:]
changeSlice(s1)
fmt.Printf("s:%v, len of s:%v, cap of s:%v \n", s, len(s), cap(s))
fmt.Printf("changeSlice函数后, s1:%v, len of s1:%v, cap of s1:%v \n", s1, len(s1), cap(s1))
}
func changeSlice(s1 []int) {
s1[0] = -1
s1 = append(s1, 10, 11, 12, 13, 14, 15)
fmt.Printf("changeSlice函数内, s1:%v, len of s1:%v, cap of s1:%v \n", s1, len(s1), cap(s1))
}
打印结果:
changeSlice函数内, s1:[-1 0 10 11 12 13 14 15], len of s1:8, cap of s1:8
s:[0 0 0 0 0 0 0 0 -1 0], len of s:10, cap of s:12
changeSlice函数后, s1:[-1 0], len of s1:2, cap of s1:4
结论:虽然切片是引用传递,实际指的是元素数据存储为引用,但切片参数仍然是不同的slice header。有点儿像C++的指针,两个指针指向的数据是同一份地址,但是两个指针本身是不同的。
所以函数changeSlice()内的s1,函数外的s1,旧切片s,三者指向的是同一块数据,一处修改即生效。但是函数changeSlice()内的s1,函数外的s1代表的是两个不同的slice header,函数执行只是修改函数内s1的slice header,函数外面s1的slice header不受影响,长度仍然是2,capacity仍然是4
举例13:多次截取切片后赋值
s := []int{0, 1, 2, 3, 4}
s = append(s[:2], s[3:]...)
fmt.Printf("s:%v, len(s)=%v, cap(s)=%v \n", s, len(s), cap(s))
v := s[4]
fmt.Printf("v=%v", v)
打印结果:
s:[0 1 3 4], len(s)=4, cap(s)=5
panic: runtime error: index out of range [4] with length 4
goroutine 1 [running]:
main.main()
结论:执行append(s[:2],s[3:]...)后,s中有4个元素,capacity仍然为5,使用下标访问s时使用的是逻辑长度,认为是越界
举例14:切片超过256时,扩容时的公式
s := make([]int, 512)
s = append(s, 1)
fmt.Printf("len(s)=%v,cap(s)=%v", len(s), cap(s))
打印结果:len(s)=513,cap(s)=848
结论:切片中元素超过512时,扩容公式不是直接翻倍,而是每次递增(N/4 + 192),直到值达到需求,其中的192=(3*256)/4
按照上面的公式,512 +(512/4+192) = 832个元素
但是为什么这里容量显示是848呢?这关联到golang的内存对齐
为了更好地进行内存空间对齐,golang 允许产生一些有限的内部碎片,对拟申请空间的 object 进行大小补齐,最终 6656 byte 会被补齐到 6784 byte 的这一档次,各个档次表如下所示:
// class bytes/obj bytes/span objects tail waste max waste min align
// 1 8 8192 1024 0 87.50% 8
// 2 16 8192 512 0 43.75% 16
// 3 24 8192 341 8 29.24%
// ...
// 48 6528 32768 5 128 6.23% 128
// 49 6784 40960 6 256 4.36% 128刚才计算出来的832元素,每个int占8个字节,所以832 * 8字节 = 6656字节
所以我们需要6656字节时,根据上面表格,落在6784这一档,golang帮我们申请了6784个字节,
6784字节 / 8字节 = 848个int元素
最终计算得到capacity为848
本篇总结:
1. 切片的capacity可以认为是物理意义上的空间;而len是罗辑意义上的元素个数
2. 根据下标访问切片时,golang的执行的是逻辑判断,不能大于或等于len的值,否则会认为是越界,发生panic
3. 切片在函数参数中传递时是引用传递,但这里的引用指的是存储的数据指向同一份。但函数内外的参数仍然是不同的slice header,就像两个指针一样
4. 切片元素超过256时,切片扩容不再是简单的翻倍,而是有个递增公式,每次增加为N/4+192。但golang申请内存时还有内存对齐的问题,有个档次表。申请内存时,在哪个档则采用这个档的值
相关文章:

golang的切片使用总结二
如果没看golang切片的第一篇总结博客 golang的切片使用总结一-CSDN博客 ,请浏览之 举例9:make([]int, a, b)后访问下标a的元素 s : make([]int, 10, 12) v : s[10] fmt.Printf("v:%v", v) 打印结果: panic: runtime error: index …...
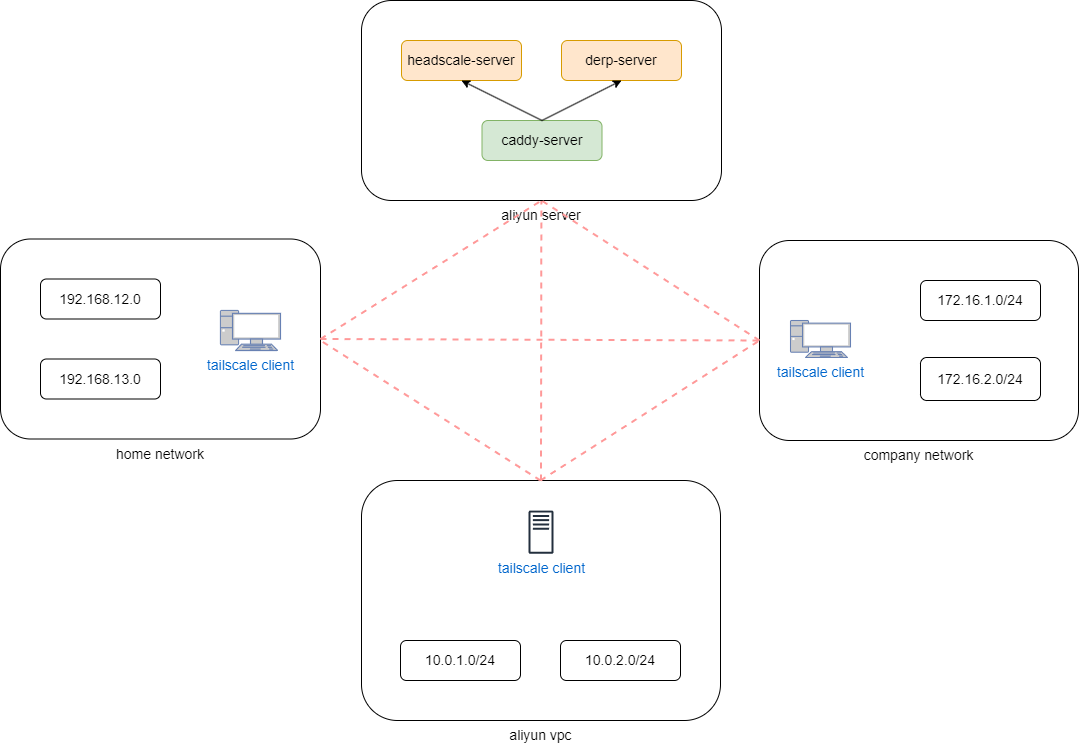
tailscale自建headscale和derp中继
tailscale derp中继服务简介 tailscale是一个基于WireGuard的零配置软件,它可以轻松地在多台设备之间建立点对点加密连接。 derp服务器是tailscale网络的重要组成部分。它作为tailscale客户端之间的中继,帮助客户端找到并连接到其他客户端设备。 但Tailscale 官方…...
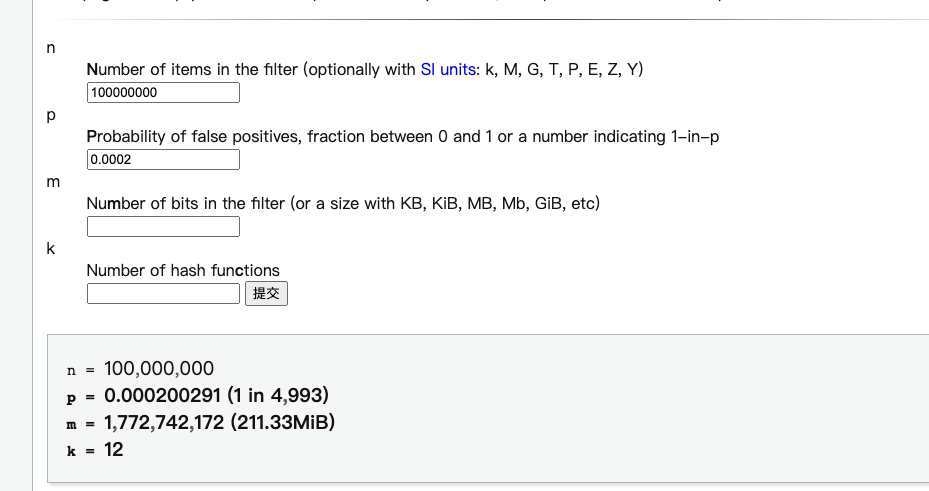
布隆过滤器的使用
布隆过滤器简介 Bloom Filter(布隆过滤器)是一种多哈希函数映射的快速查找算法。它是一种空间高效的概率型数据结构,通常应用在一些需要快速判断某个元素是否属于集合,但是并不严格要求100%正确的场合。 布隆过滤器的优势在于,利用很少的空…...

Web开发-单例模式
目录 单例模式介绍代码实现单例模式 单例模式介绍 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点。单例模式可以通过private属性实现。通过将类的构造函数设为private,可以防止类在外部被实例化。单例模式通…...
MySQL:温备份和恢复-mysqldump (4)
介绍 温备:同样是在数据库运行的时候进行备份的,但对当前数据库的操作会产生影响。(只可以读操作,不可以写操作) 温备份的优点: 1.可在表空间或数据文件级备份,备份时间短。 2.备份时数据库依然…...
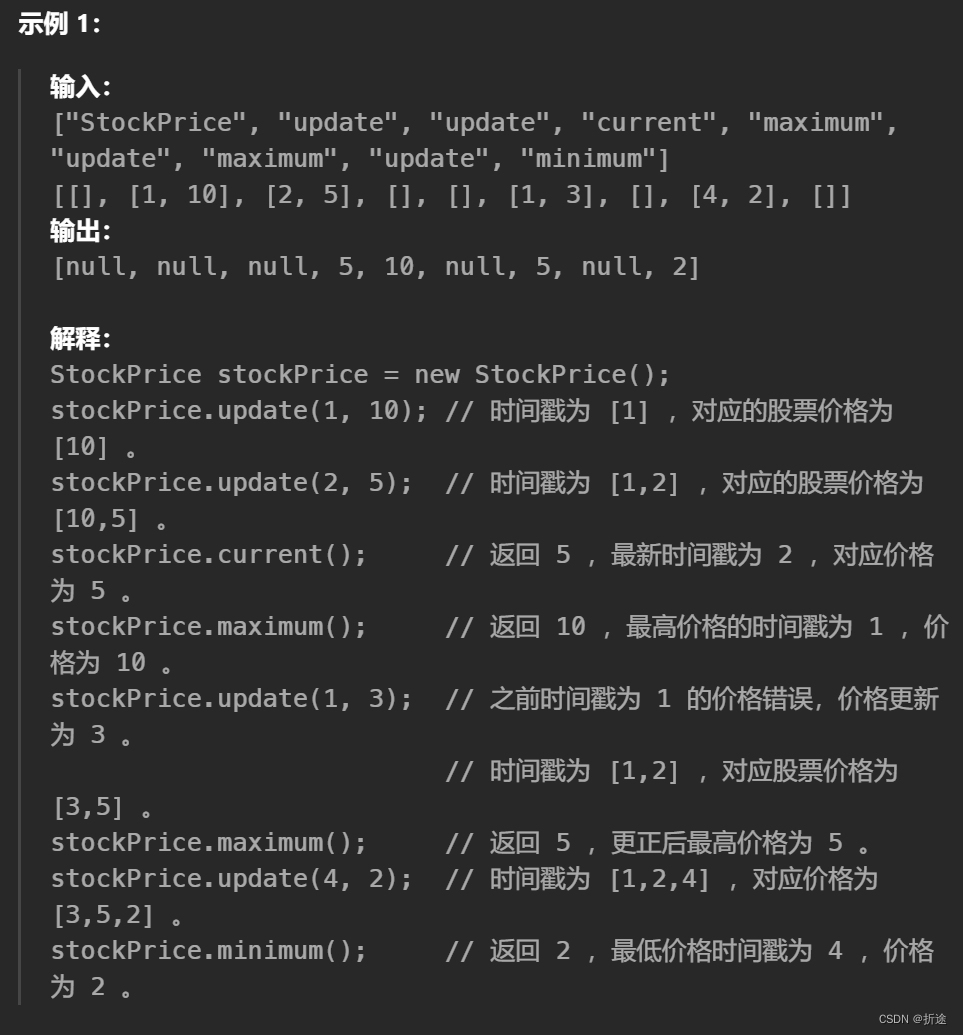
【力扣每日一题】2023.10.8 股票价格波动
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题是程序设计题,要我们实现一个类,一共是四个功能,第一个是给一个时间戳和价格,表示该…...

Linux隐藏文件或文件夹
在Linux中,以点(.)开头的文件或文件夹是隐藏文件或隐藏文件夹。要创建一个隐藏文件或文件夹,可以使用以下命令: 创建隐藏文件: touch .filename这将在当前目录下创建一个名为 “.filename” 的隐藏文件。…...
leetcode - 365周赛
一,2873.有序三元组中的最大值 I 该题的数据范围小,直接遍历: class Solution {public long maximumTripletValue(int[] nums) {int n nums.length;long ans 0;for(int i0; i<n-2; i){for(int ji1; j<n-1; j){for(int kj1; k<…...

为什么mac上有的软件删除不掉?
对于Mac用户来说,软件卸载通常是一个相对简单的过程。然而,有时你可能会发现某些软件似乎“顽固不化”,即使按照常规方式尝试卸载,也依然存在于你的电脑上。这到底是为什么呢?本文将探讨这一问题的可能原因。 1.卸载失…...
【vue3】wacth监听,监听ref定义的数据,监听reactive定义的数据,详解踩坑点
假期第二篇,对于基础的知识点,我感觉自己还是很薄弱的。 趁着假期,再去复习一遍 之前已经记录了一篇【vue3基础知识点-computed和watch】 今天在学习的过程中发现,之前记录的这一篇果然是很基础的,很多东西都讲的不够…...
跨境电商如何通过软文建立品牌形象?
在全球产业链结构重塑后的今天,越来越多的企业意识到想要可持续发展,就需要在建立品牌形象,在用户心中留下深刻印象,那么应该如何有效建立品牌形象呢?可以利用软文来打造品牌形象,接下来媒介盒子就告诉大家…...
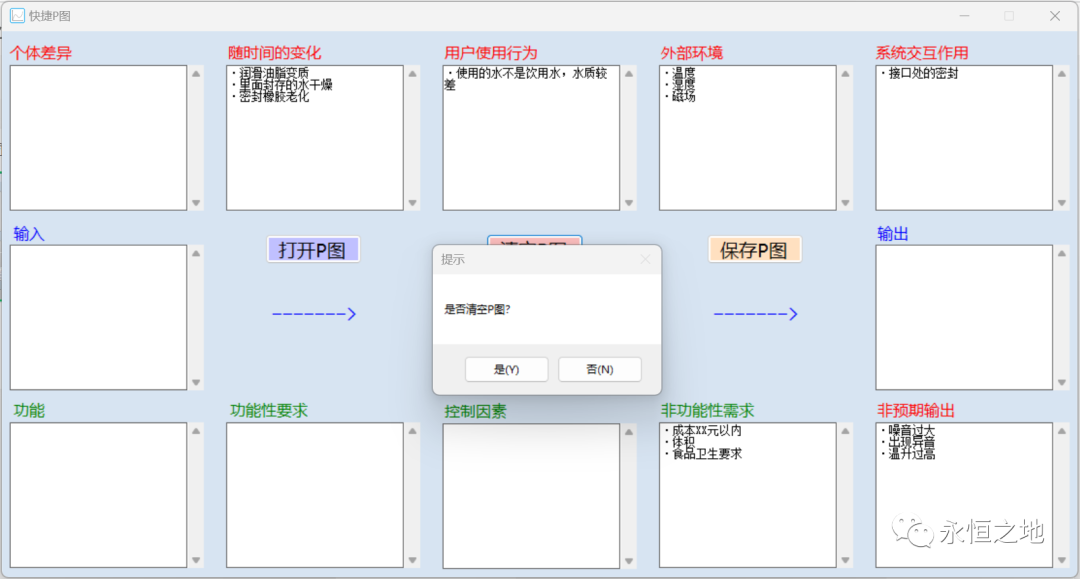
我做了一个简易P图(参数图)分析软件
P图(即参数图,Parameter Diagram),是一个结构化的工具,帮助大家对产品更好地进行分析。 典型P图格式 P图最好是和FMEA软件联动起来,如国可工软的FMEA软件有P图分析这个功能。 单纯的P图分析软件很少,为了方便做P图分…...
:状态,按键分区,算子状态,状态后端。容错机制,检查点,保存点。状态一致性。flink与kafka整合)
209.Flink(四):状态,按键分区,算子状态,状态后端。容错机制,检查点,保存点。状态一致性。flink与kafka整合
一、状态 1.概述 算子任务可以分为有状态、无状态两种。 无状态:filter,map这种,每次都是独立事件有状态:sum这种,每次处理数据需要额外一个状态值来辅助。这个额外的值就叫“状态”2.状态的分类 (1)托管状态(Managed State)和原始状态(Raw State) 托管状态就是由…...
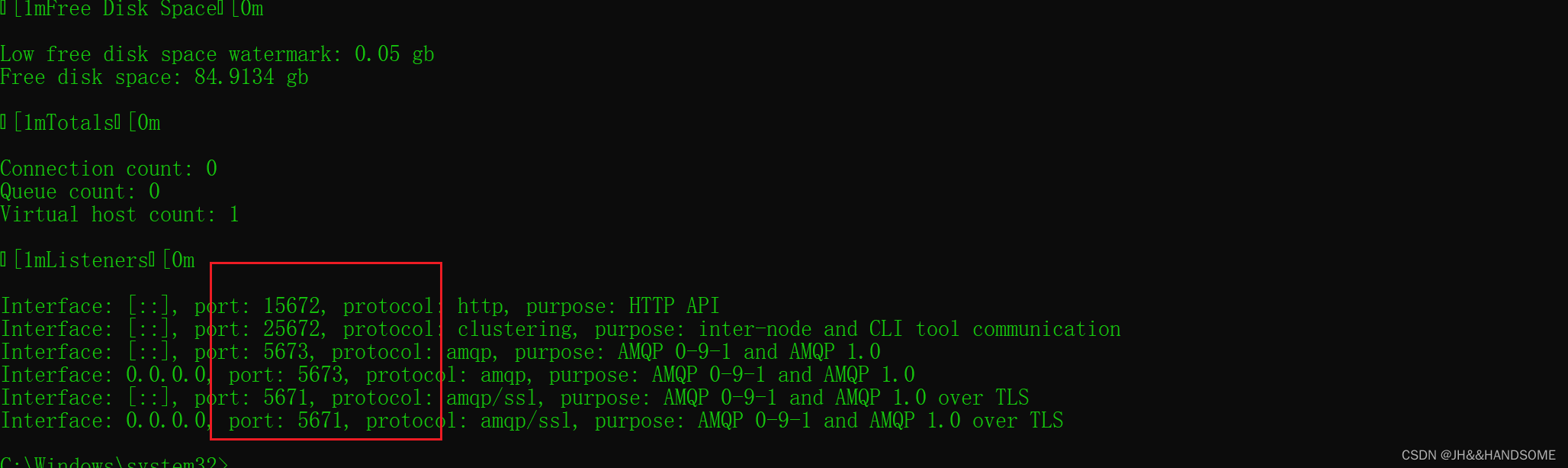
rabbitmq查看节点信息命令失败
不影响访问rabbitmq,但是无法使用 命令查看节点信息 等 查看节点信息命令:rabbitmq-diagnostics status --node rabbitJHComputer Error: unable to perform an operation on node ‘rabbitJHComputer‘. Please see diagnostics informatio rabbitmq-…...
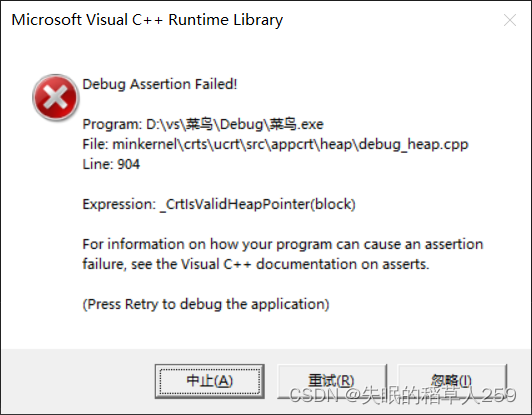
c语言动态内存分布
前言: 随着我们深入的学习c语言,之前使用的静态内存分配已经难以满足我们的实际需求。比如前面我们的通讯录功能的实现,如果只是静态内存分配,那么也就意味着程序开始的内存分配大小就是固定的,应该开多大的空间呢&am…...

1.3.2有理数减法(第一课时)作业设计
【学习目标】 1.理解有理数减法法则,能熟练地进行有理数的减法运算. 2.感受有理数减法与加法对立统一的辨证思想,体会转化的思想方法....
vue3 -- ts封装 Turf.js地图常用方法
Turf.js中文网 地理空间分析库,处理各种地图算法 文档地址 安装 Turf 库 npm install @turf/turf创建src/hooks/useTurf.ts 文件1:获取线中心点 效果: 代码: useTurf.ts import * as turf from @turf/turf// 获取线中心点 export class CenterPointOfLine {...
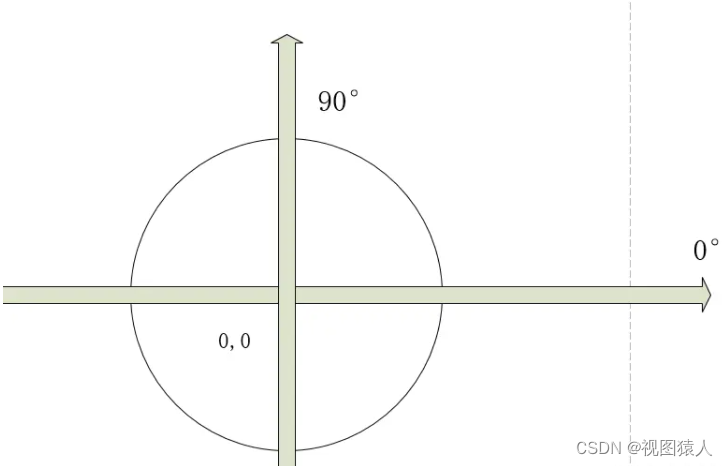
Qt之实现圆形进度条
在Qt自带的控件中,只有垂直进度条、水平进度条两种。 在平时做页面开发时,有些时候会用到圆形进度条,比如说:下载某个文件的下载进度。 展示效果,如下图所示: 实现这个功能主要由以下几个重点:…...

C# 图解教程 第5版 —— 第1章 C# 和 .NET 框架
文章目录 1.1 在 .NET 之前1.2 .NET 时代1.2.1 .NET 框架的组成1.2.2 大大改进的编程环境 1.3 编译成 CIL1.4 编译成本机代码并执行1.5 CLR1.6 CLI1.7 各种缩写1.8 C# 的演化1.9 C# 和 Windows 的演化(*) 1.1 在 .NET 之前 MFC(Microsoft Fou…...
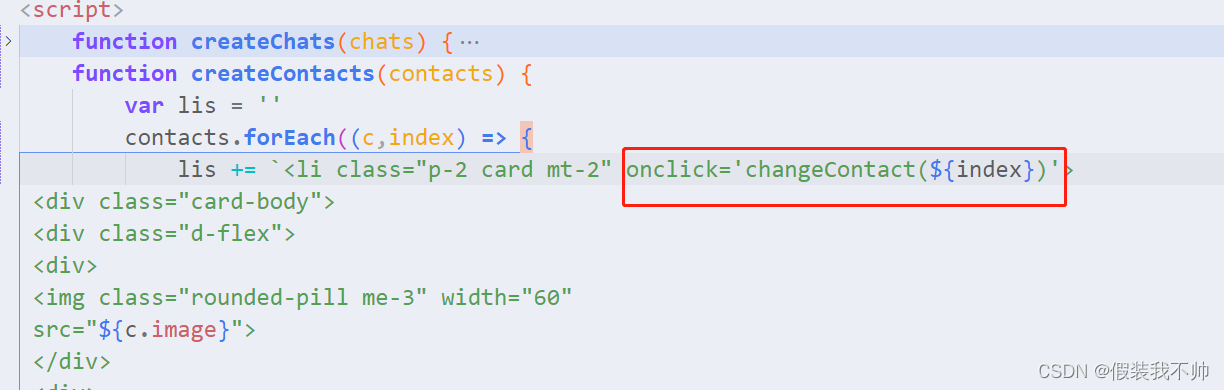
electronjs入门-聊天应用程序,与Electron.js通信
随着第一章中构建的应用程序,我们将开始将其与Electron框架中的模块集成,并以此为基础,以更实用的方式了解它们。 过程之间的通信 根据第二章中的解释,我们将发送每个进程之间的消息;具体来说联系人和聊天࿱…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
