ds套dp——考虑位置转移or值域转移:CF1762F
https://www.luogu.com.cn/problem/CF1762F
- 分析性质,就是我们选的数要么递增,要么递减(非严格)
- 然后很明细是ds套dp, f i f_i fi 表示以 i i i 开头的答案
- 然后考虑如何转移(ds套dp难点反而在转移而不是状态,因为要考虑如何和ds结合)
- 转移的话,要么从位置考虑,要么从值域考虑
- 从值域考虑,就从后面比它大且最小的转移,似乎不知道怎么搞
- 从位置考虑,就是从第一个在 [ a i , a i + k ] [a_i,a_i+k] [ai,ai+k] 内的数转移。我们考虑会漏掉值域在 [ a i + 1 , a j − 1 ] [a_i+1,a_j-1] [ai+1,aj−1] 的数,但这可以直接套ds来做了。至于大于 a j a_j aj 的会在 f j f_j fj 里算
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 500010
//#define M
//#define mo
struct node {int x, id; bool operator < (const node &A) const {return id < A.id; }
}b[N];
int n, m, i, j, k, T;
int ans, a[N], mp[N], nxt[N], f[N], l;
set<node>s;
set<node>::iterator it; struct Binary_tree {int cnt[N]; void add(int x, int y) {while(x<N) cnt[x]+=y, x+=x&-x; }int que(int x) {int ans = 0; while(x) ans+=cnt[x], x-=x&-x; return ans; }
}Bin;void calc() {for(i=1; i<=n; ++i) b[i].x = a[i], b[i].id = i; auto cmp = [&] (node x, node y) -> bool {if(x.x == y.x) return x.id > y.id; return x.x > y.x; }; sort(b+1, b+n+1, cmp); s.clear(); for(i=l=1; i<=n; ++i) {while(b[l].x>b[i].x+k) s.erase(b[l]), ++l; it = s.upper_bound({0, b[i].id}); if(it == s.end()) nxt[b[i].id] = 0; else nxt[b[i].id] = (it -> id); s.insert(b[i]); }
// for(i = 1; i <= n; ++i) printf("%d ", nxt[i]); printf("\n"); for(i=n; i>=1; --i) {j=nxt[i]; f[i]=f[j]+1; if(nxt[i]==0) f[i]+=Bin.que(a[i]+k)-Bin.que(a[i]-1); else f[i]+=Bin.que(a[nxt[i]]-1)-Bin.que(a[i]-1); ans+=f[i]; Bin.add(a[i], 1);
// printf("%lld (%lld %lld)", f[i], f[j]); }
// printf("\n"); for(i=1; i<=n; ++i) Bin.add(a[i], -1);
}signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);T=read();while(T--) {n=read(); k=read(); ans=0; for(i=1; i<=n; ++i) {a[i]=read(), mp[a[i]]++, ans-=mp[a[i]]; }
// printf("> %lld\n", ans); `calc(); reverse(a+1, a+n+1); calc(); for(i=1; i<=n; ++i) mp[a[i]]=0; printf("%lld\n", ans); }return 0;
}相关文章:

ds套dp——考虑位置转移or值域转移:CF1762F
https://www.luogu.com.cn/problem/CF1762F 分析性质,就是我们选的数要么递增,要么递减(非严格)然后很明细是ds套dp, f i f_i fi 表示以 i i i 开头的答案然后考虑如何转移(ds套dp难点反而在转移而不是…...
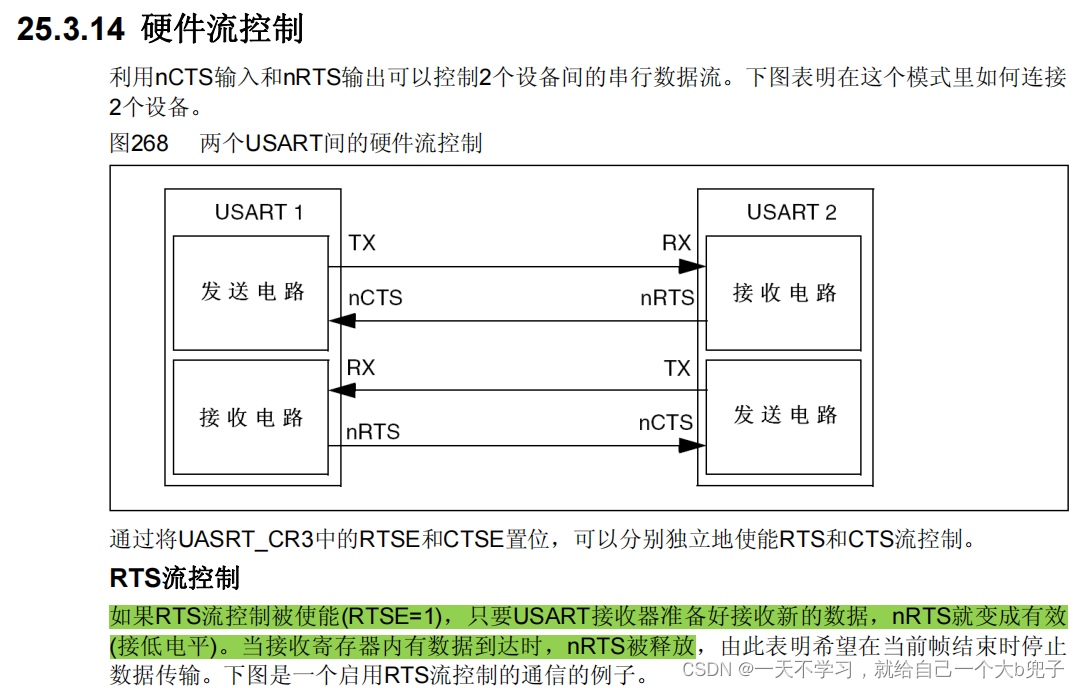
stm32的GPIO寄存器操作以及GPIO外部中断,串口中断
一、学习参考资料 (1)正点原子的寄存器源码。 (2)STM32F103最小系统板开发指南-寄存器版本_V1.1(正点) (3)STM32F103最小系统板开发指南-库函数版本_V1.1(正点&a…...
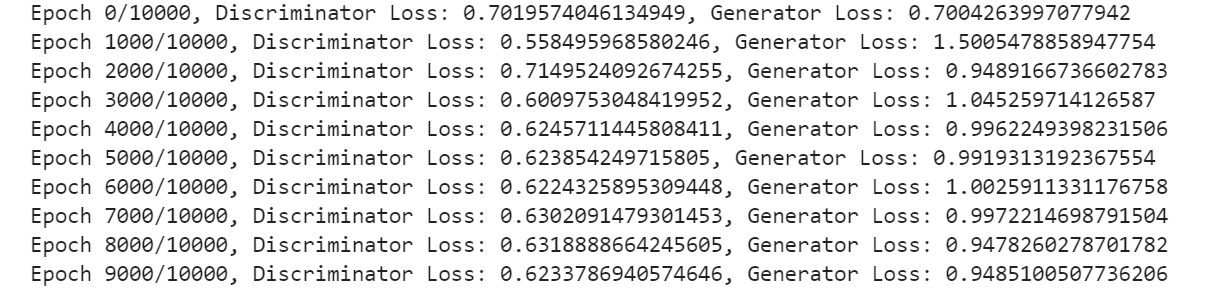
生成对抗网络入门案例
前言 生成对抗网络(Generative Adversarial Networks,简称GANs)是一种用于生成新样本的机器学习模型。它由两个主要组件组成:生成器(Generator)和判别器(Discriminator)。生成器尝试…...
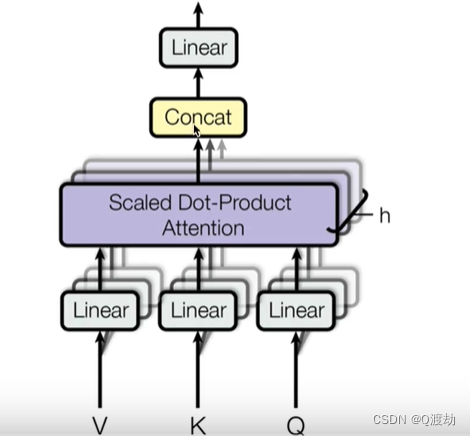
多头注意力机制
1、什么是多头注意力机制 从多头注意力的结构图中,貌似这个所谓的多个头就是指多组线性变换,但是并不是,只使用了一组线性变换层,即三个变换张量对 Q、K、V 分别进行线性变换,这些变化不会改变原有张量的尺寸…...
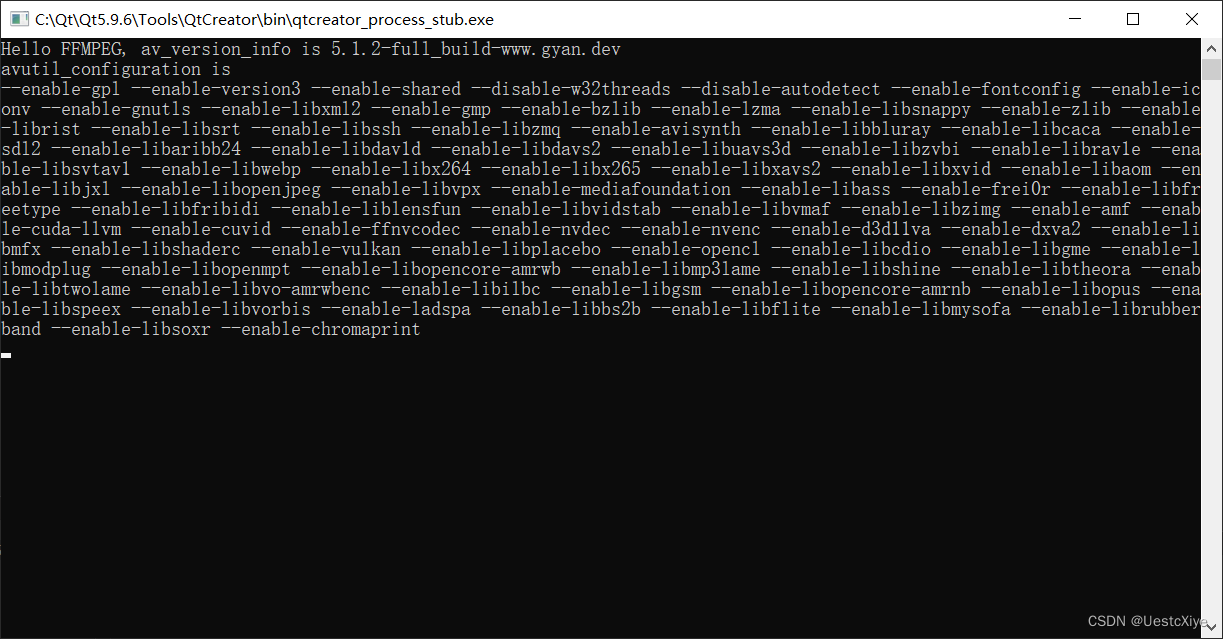
Qt + FFmpeg 搭建 Windows 开发环境
Qt FFmpeg 搭建 Windows 开发环境 Qt FFmpeg 搭建 Windows 开发环境安装 Qt Creator下载 FFmpeg 编译包测试 Qt FFmpeg踩坑解决方法1:换一个 FFmpeg 库解决方法2:把项目改成 64 位 后记 官方博客:https://www.yafeilinux.com/ Qt开源社区…...

[网鼎杯 2020 白虎组]PicDown python反弹shell proc/self目录的信息
[网鼎杯 2020 白虎组]PicDown - 知乎 这里确实完全不会 第一次遇到一个只有文件读取思路的题目 这里也确实说明还是要学学一些其他的东西了 首先打开环境 只存在一个框框 我们通过 目录扫描 抓包 注入 发现没有用 我们测试能不能任意文件读取 ?url../../../../etc/passwd …...
SDL2绘制ffmpeg解析的mp4文件
文章目录 1.FFMPEG利用命令行将mp4转yuv4202.ffmpeg将mp4解析为yuv数据2.1 核心api: 3.SDL2进行yuv绘制到屏幕3.1 核心api 4.完整代码5.效果展示6.SDL2事件响应补充6.1 处理方式-016.2 处理方式-02 本项目采用生产者消费者模型,生产者线程:使用ffmpeg将m…...

决策树C4.5算法的技术深度剖析、实战解读
目录 一、简介决策树(Decision Tree)例子: 信息熵(Information Entropy)与信息增益(Information Gain)例子: 信息增益比(Gain Ratio)例子: 二、算…...
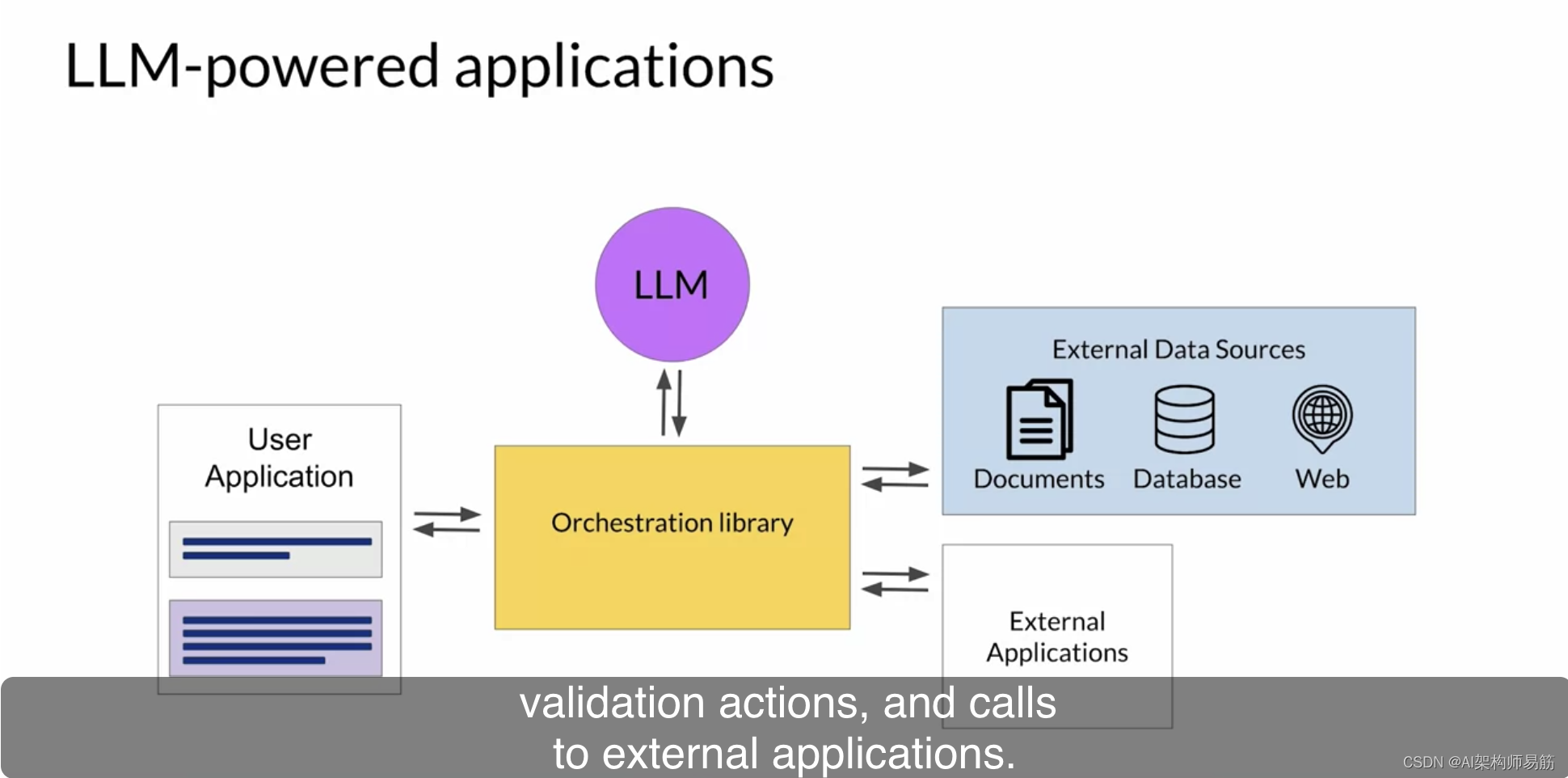
LLMs Python解释器程序辅助语言模型(PAL)Program-aided language models (PAL)
正如您在本课程早期看到的,LLM执行算术和其他数学运算的能力是有限的。虽然您可以尝试使用链式思维提示来克服这一问题,但它只能帮助您走得更远。即使模型正确地通过了问题的推理,对于较大的数字或复杂的运算,它仍可能在个别数学操…...
【12】c++设计模式——>单例模式练习(任务队列)
属性: (1)存储任务的容器,这个容器可以选择使用STL中的队列(queue) (2)互斥锁,多线程访问的时候用于保护任务队列中的数据 方法:主要是对任务队列中的任务进行操作 &…...
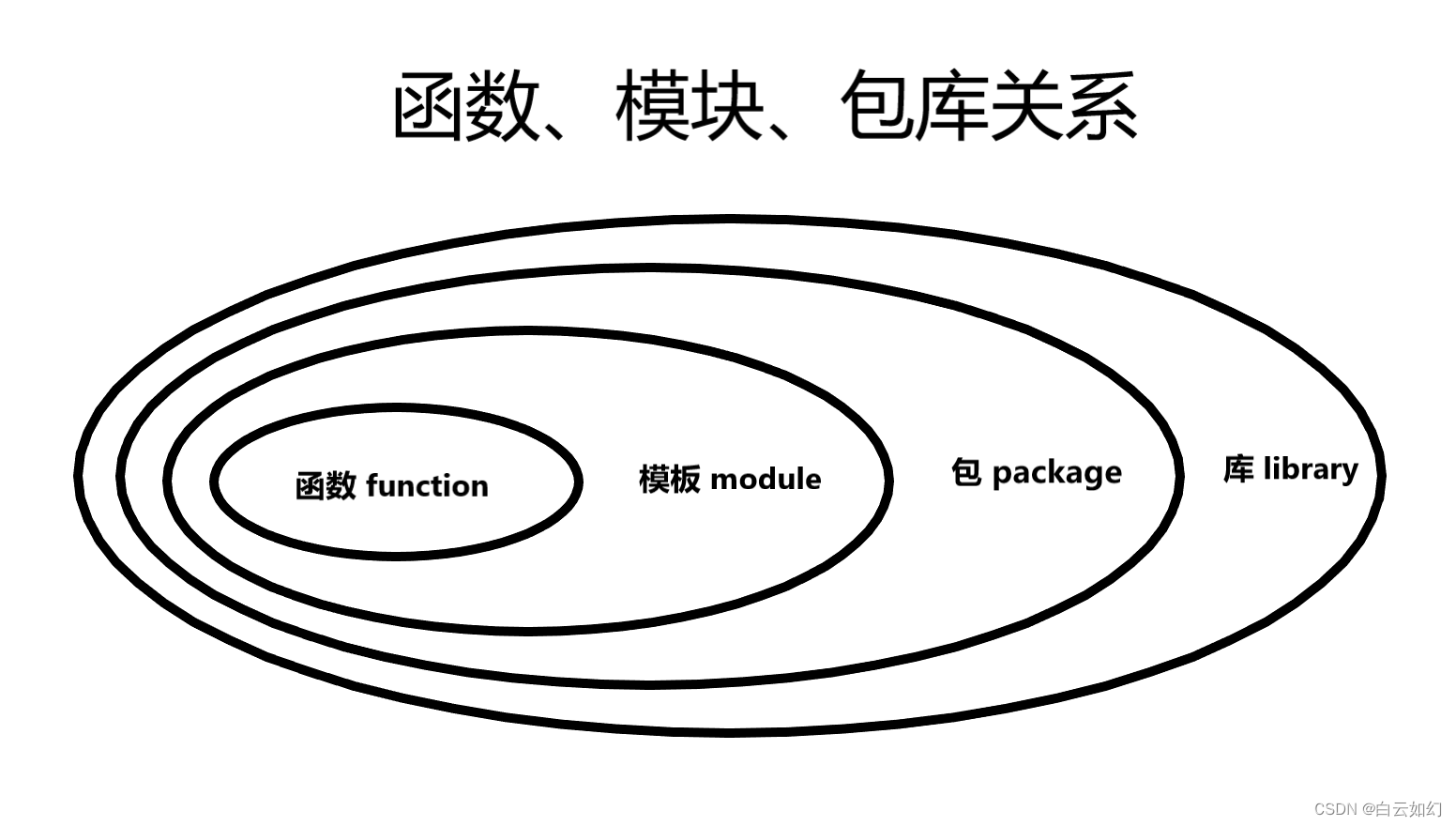
Python之函数、模块、包库
函数、模块、包库基础概念和作用 A、函数 减少代码重复 将复杂问题代码分解成简单模块 提高代码可读性 复用老代码 """ 函数 """# 定义一个函数 def my_fuvtion():# 函数执行部分print(这是一个函数)# 定义带有参数的函数 def say_hello(n…...

SQL创建与删除索引
索引创建、删除与使用: 1.1 create方式创建索引:CREATE [UNIQUE – 唯一索引 | FULLTEXT – 全文索引 ] INDEX index_name ON table_name – 不指定唯一或全文时默认普通索引 (column1[(length) [DESC|ASC]] [,column2,…]) – 可以对多列建立组合索引 …...
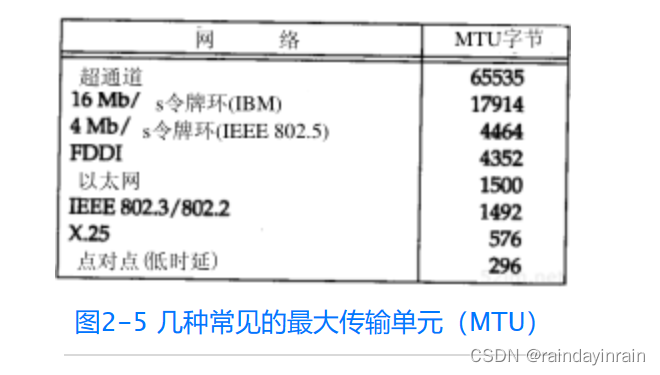
网络协议--链路层
2.1 引言 从图1-4中可以看出,在TCP/IP协议族中,链路层主要有三个目的: (1)为IP模块发送和接收IP数据报; (2)为ARP模块发送ARP请求和接收ARP应答; (3…...

HDLbits: Count clock
目前写过最长的verilog代码,用了将近三个小时,编写12h显示的时钟,改来改去,估计只有我自己看得懂(吐血) module top_module(input clk,input reset,input ena,output pm,output [7:0] hh,output [7:0] mm,…...

【1day】用友移动管理系统任意文件上传漏洞学习
注:该文章来自作者日常学习笔记,请勿利用文章内的相关技术从事非法测试,如因此产生的一切不良后果与作者无关。 目录 一、漏洞描述 二、影响版本 三、资产测绘 四、漏洞复现...

【c++】向webrtc学习容器操作
std::map的key为std::pair 时的查找 std::map<RemoteAndLocalNetworkId, size_t> in_flight_bytes_RTC_GUARDED_BY(&lock_);private:using RemoteAndLocalNetworkId = std::pair<uint16_t, uint16_t...
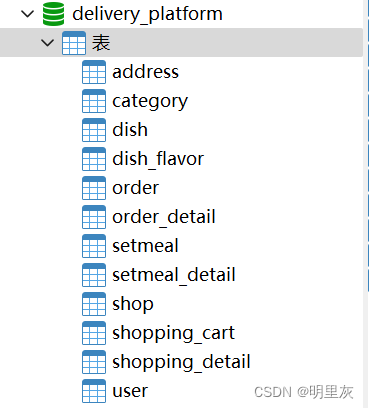
SpringBoot+Vue3外卖项目构思
SpringBoot的学习: SpringBoot的学习_明里灰的博客-CSDN博客 实现功能 前台 用户注册,邮箱登录,地址管理,历史订单,菜品规格,购物车,下单,菜品浏览,评价,…...

【AI视野·今日NLP 自然语言处理论文速览 第四十七期】Wed, 4 Oct 2023
AI视野今日CS.NLP 自然语言处理论文速览 Wed, 4 Oct 2023 Totally 73 papers 👉上期速览✈更多精彩请移步主页 Daily Computation and Language Papers Contrastive Post-training Large Language Models on Data Curriculum Authors Canwen Xu, Corby Rosset, Luc…...

c++的lambda表达式
文章目录 1 lambda表达式2 捕捉列表 vs 参数列表3 lambda表达式的传递3.1 函数作为形参3.2 场景1:条件表达式3.3 场景2:线程的运行表达式 1 lambda表达式 lambda表达式可以理解为匿名函数,也就是没有名字的函数,既然是函数&#…...

电梯安全监测丨S271W无线水浸传感器用于电梯机房/电梯基坑水浸监测
城市化进程中,电梯与我们的生活息息相关。高层住宅、医院、商场、学校、车站等各种商业体建筑、公共建筑中电梯为我们生活工作提供了诸多便利。 保障电梯系统的安全至关重要!特别是电梯机房和电梯基坑可通过智能化改造提高其安全性和稳定性。例如在暴风…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
