pytorch_神经网络构建2(数学原理)
文章目录
- 深层神经网络
- 多分类深层网络
- 反向传播算法
- 优化算法
- 动量算法
- Adam 算法
深层神经网络
分类基础理论:
交叉熵是信息论中用来衡量两个分布相似性的一种量化方式
之前讲述二分类的loss函数时我们使用公式-(y*log(y_)+(1-y)*log(1-y_)进行误差计算
y表示真实值,y_表示预测值
def binary_loss(y_pred, y):logits = (y * y_pred.clamp(1e-12).log() + (1 - y) * (1 - y_pred).clamp(1e-12).log()).mean()return -logits
交叉熵的一般公式为:
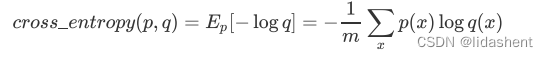
那么二分类时公式可以写作:
其中sigmoid(x)=y_
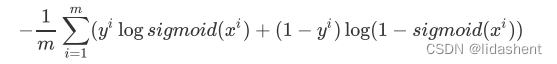
这就是二分类的loss函数,那么如果我们要进行多分类,比如三分类,十分类,参照此交叉熵方式改进是可行的
而pytorch已经为我们预设了此函数,它将根据我们神经网络输出的分类个数自动进行公式计算
其中每个分类的概率为:
对于输出层的每个输出x1,x2,x3,每个求指数e^x1等等,然后求和,再算出每个值大小占比,即其概率
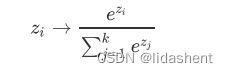
多分类深层网络
我们可以举个例子,比如mnist手写识别案例,它有十个分类,据此实践交叉熵公式
其中网络的训练是类似的,不同的是loss函数
train_set=mnist.MNIST("./data",train=True,download=True)
test_set=mnist.MNIST('./data',train=False,download=True)
a_data, a_label = train_set[0]
从网络上下载mnist手写数据,然后将其类型转化为tensor类型
查看数据

每张图片28*28,可以看做一组784列的01数据,数据范围为0~255
将所有数据拉平并且标准化,方便输入
from torch.utils.data import DataLoader
def data_tf(x):x = np.array(x, dtype='float32') / 255x = (x - 0.5) / 0.5 # 标准化x = x.reshape((-1,)) # 拉平x = torch.from_numpy(x)return x
train_set = mnist.MNIST('./data', train=True, transform=data_tf, download=True) # 重新载入数据集,申明定义的数据变换
test_set = mnist.MNIST('./data', train=False, transform=data_tf, download=True)
当数据集巨大,不能一次导入内存时,往往采取划分迭代方式批次录入,使用数据迭代器
from torch.utils.data import DataLoader
# 数据迭代器
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
test_data = DataLoader(test_set, batch_size=128, shuffle=False)
a, a_label = next(iter(train_data))
数据迭代器是一个对象,从其中取出数据需要使用迭代器,他没有下标
数据已经准备完毕
然后定义神经网络结构和参数,定义损失函数和wb参数优化器,然后进行迭代训练wb
pytroch已经预设了交叉熵函数
mnNet=nn.Sequential(nn.Linear(784,256),nn.ReLU(),nn.Linear(256, 128),nn.ReLU(),nn.Linear(128, 64),nn.ReLU(),nn.Linear(64, 20),nn.ReLU(),nn.Linear(20, 10))
losser=nn.CrossEntropyLoss()
optimizer=torch.optim.SGD(mnNet.parameters(),1e-1)
开始迭代训练,其中我们需要统计每个批次的准确率和loss值,方便我们直观的看到准确率和loss的变化
我们需要求出一次迭代数据集训练中所有批次的准确率之和,然后比批次的迭代次数
就得到了每个批次的平均准确率,来作为这一次训练迭代的准确率结果
不实时展示每个批次的准确率和loss是因为单个批次准确率波动范围大,不能准确显示一次迭代训练的效果
接下来我们对数据集进行20次迭代训练
训练和测试不同的地方在于,训练集不需要更新wb参数,也不需要loss进行反向传播
losses=[]
acces=[]
eval_losses=[]
eval_acces=[]
for e in range(20):train_loss=0train_acc=0mnNet.train()for im,label in train_data:im=Variable(im)label=Variable(label)out=mnNet(im)loss=losser(out,label)optimizer.zero_grad()loss.backward()optimizer.step()train_loss+=loss.item()_,pred=out.max(1)num_currect=(pred==label).sum()acc=num_currect/im.shape[0]train_acc+=acclosses.append(train_loss/len(train_data))acces.append(train_acc/len(train_data))eval_loss=0eval_acc=0mnNet.eval()for im,label in test_data:im=Variable(im)label=Variable(label)out=mnNet(im)loss=losser(out,label)eval_loss+=loss.item()_,pred=out.max(1)num_currect=(pred==label).sum()acc=num_currect/im.shape[0]eval_acc+=acceval_losses.append(eval_loss/len(test_data))eval_acces.append(eval_acc/len(test_data))print('epoch: {}, Train Loss: {:.6f}, Train Acc: {:.6f}, Eval Loss: {:.6f}, Eval Acc: {:.6f}'.format(e, train_loss / len(train_data), train_acc / len(train_data), eval_loss / len(test_data), eval_acc / len(test_data)))
print("训练完成")
我们可以实际查看一下预测的效果如何
取出一部分test_data值进行测试
im,label=next(iter(test_data))
y_=mnNet(im)
print("真实值:{}".format(label))
print("预测值:{}".format(y_.max(1)))

看起对于这一批次预测的较为准确,那么实际的训练变化曲线呢?
然后我们分别绘制train acc ,train loss,test acc,test loss的变化情况
import matplotlib.pyplot as plt
%matplotlib inline
plt.plot(np.arange(len(acces)), acces)
plt.title('train acc')
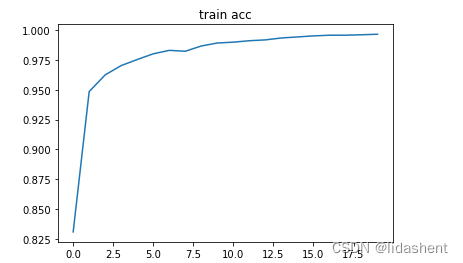
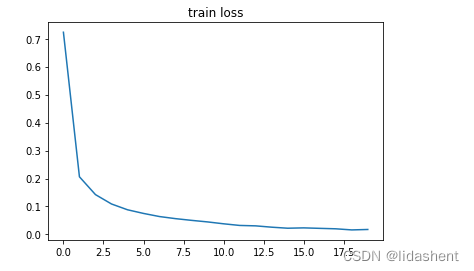
plt.title('train loss')
plt.plot(np.arange(len(losses)), losses)
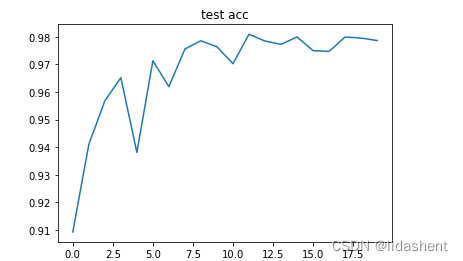
plt.plot(np.arange(len(eval_acces)), eval_acces)
plt.title('test acc')
plt.plot(np.arange(len(eval_losses)), eval_losses)
plt.title('test loss')
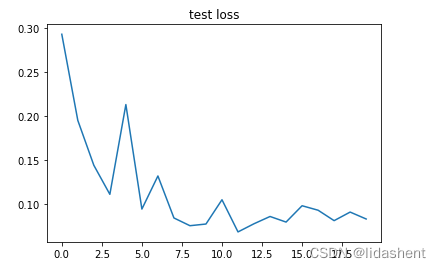
可以观察到随着训练的进行,wb参数的优化导致了训练集上的准确性在不断提高,在测试集上准确率也在不断提高
训练集上的loss在不断降低,测试集上的loss也在不断降低,这是一个不错的结果
反向传播算法
构建神经网络模型重要的一环是设置loss函数,而决定模型的优化方向取决于loss函数收敛的方向
即loss向0收敛的方向
怎么得到那些参数的梯度来进行持续的更新wb到合适的位置呢?梯度在网络中反向传递时又是如何更新的呢?
这得益于一种算法思想:链式法则
在神经网络发展初期提出神经元感知机30年后,这种算法才被创造和普及,期间人们对于ai的建设一直在质疑声中缓慢进行,
对此只能感叹,很多看似显而易见的想法只有在事后才变得显而易见
链式法则的思想在于,将复杂的函数进行逐个拆分化
我们设想一个简单的神经网络,公式可以写为f(x,y,z)=(x+y)z
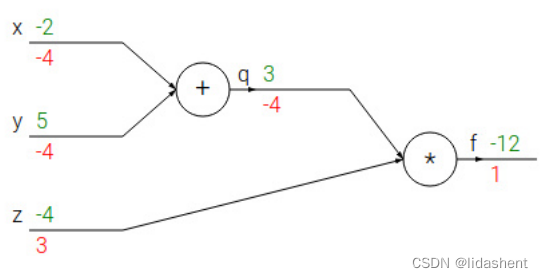
我们需要对x,y,z进行参数优化,降低他们的错误梯度,我们需要得到
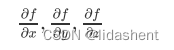
那么可以将函数简化,假设q=x+y
那么函数可以写为f(q,z)=qz
那么问题简化为求q,z的梯度
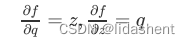
得到q的梯度后可以进一步得到x,y的梯度
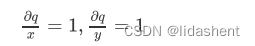
那么对于f函数来说,x,y,z的梯度结果就可以理解为:
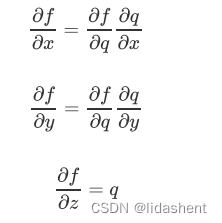
这个法则的思想在于,如果我们需要对其中的某个元素进行求导,我们只需要一层一层求导然后让结果相乘,比如f与x的关系
我们回过头来看我们设计的这个简化的神经网络,
绿色的是对应的参数值,红色的代表需要优化的梯度方向
图中的末置位梯度为1,基于此我们对这个网络中的所有参数进行更新
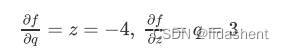
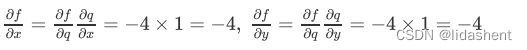
这样我们就得到了所有参数的梯度方向和大小,然后根据梯度更新参数即可
假如说前向传播是根据设定的wb进行向后计算结果的过程,反向传播就是根据结果的损失函数,向前反馈逐一更新每个wb的过程
这是一个简单的函数,
我们来看一个复杂的函数,来帮助理解链式法则和反向传播
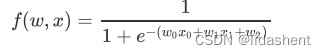
我们要更新w0,w1,w2的参数,即求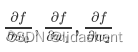
那么我们即可以对其进行链式展开
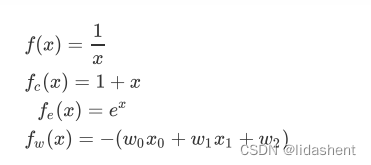
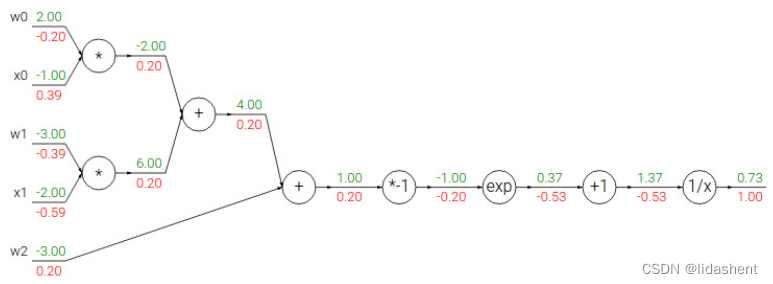
其中每个绿色数字是当前参数,红色是当前梯度,
如果对其更新梯度,则依次是1/x的导数为-1/x^2,则梯度计算为
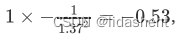
+1梯度为0,依旧为-0.53,然后导数持续向前传递
优化算法
探究优化算法的本质有助于我们设计整个神经网络,任何一个最大化问题都可以在前面加一个负号当做最小化处理
这是数学上的技巧,上述的反向传播就是一种优化算法,在数学上我们可以对其进行如下表达
对于损失函数L我们希望用它的导数L’来更新它的参数,如下设置了更新步长,也叫学习率
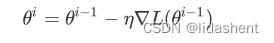
那么我们最终的求解函数是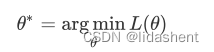
argmin代表求解这个函数L达到最小值时的参数取值
理论上来讲,我们得到的损失函数取值应该是L1>L2>L3…朝着不断降低的方向前进,直到所有参数都被放置在最合适的位置,达到模型最优解
但往往在求解最优值的过程中会得到局部最优解和鞍点
局部最优解
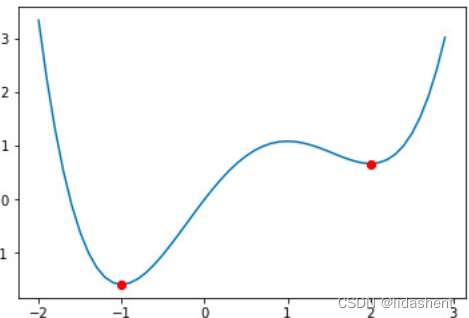
鞍点
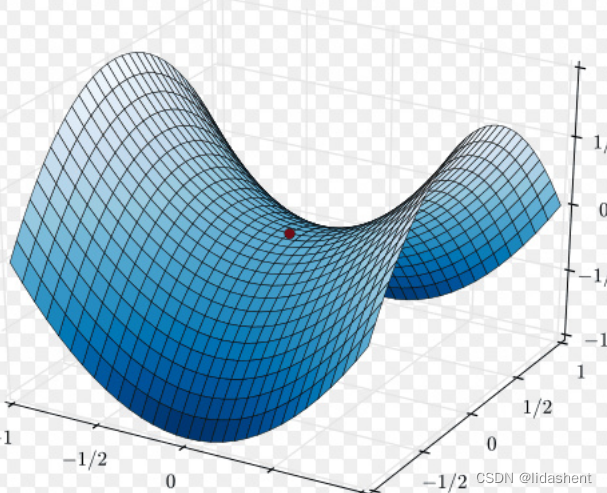
局部最优解让我们无法得到全局最优解,这往往和我们设计的步长和随机参数有关,导致模型无法进一步找到全局最小点
鞍点则意味着导数为0,函数已经陷入了死结,给人一种进入极限的感觉,这些都会无法发挥网络结构的全部实力
这确实是一个看运气的事情,然而我们平常加载数据时不会一次性将所有数据导入,而是使用数据迭代器批次加载,
无形中可以帮助我们跳过局部最小点,当然这也有运气的成分,这也是同一个模型多次训练后准确率有时会出现大范围波动的原因
现在不是感慨的时候,我们依旧需要探究优化函数的本质,让我们来论证一下优化函数是否是正确的
看看是否我们使用优化函数后误差值是否在真的在降低,还是偶然的假象
在数学中有一种泰勒展开式,可以对连续光滑可导函数的某一点x=x0处进行无限逼近,逼近到什么地步呢?这个原函数的点x0附近的值和导数都在和这个展开式无限贴合
泰勒展开式为:
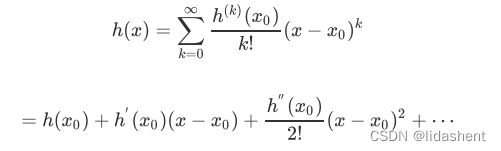
可以看到,展开的第一项为原函数的在x0处的常量,第二项为h(x0)的一阶导数h’(x0),x-x0一般记作德尔塔x,代表逼近x0的x误差范围,随着展开式的展开,对h(x0)进行不断n次求导比上求导次数阶乘n,然后乘德尔塔x的n次方,
假设原函数为e^x,我们对其在0处画出一个泰勒展开式的拟合函数图像,那么对其进行展开5次,当然我们可以展开更多次,这样展开式拟合的函数更贴合原函数
一阶展开
1+x
五阶展开
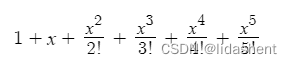
画出三者图像
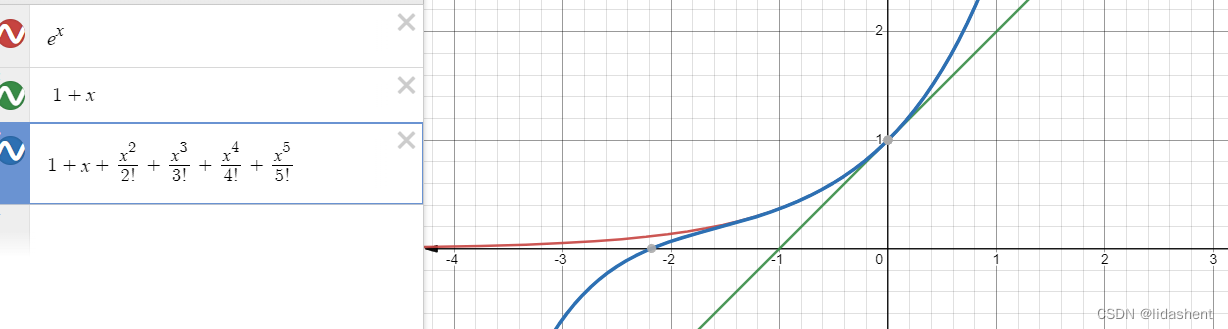
可以看到泰勒展开式随着展开的进行在不断拟合e^x的函数图像,这意味着任何一个光滑连续可导函数,都可以用泰勒展开式进行拟合,接下来我们使用泰勒展开式对神经网络训练中参数更新的函数进行论证,对loss函数进行拟合,查看它是否在对着下降的方向移动
为了方便,我们只对泰勒展开式二阶展开,我们只需要得到这个趋势就可以了
当参数只有一个时,即一维时
当前loss函数为L,预设参数为w,参数移动范围为e,即x-x0=e,x0=w,对其进行展开如下
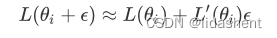
我们设置学习率为a,那么在神经网络中参数e移动的范围为e=-a*L’
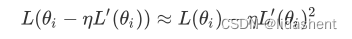
学习率a是正数,导数的平方也是正数,那么我们可以得到
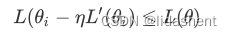
也就是在参数朝着导数的方向移动后,损失函数的值降低了,w得到了优化,准确率在提升
那么当我们设置参数w为多个时是否依旧如此呢?损失函数值是否还是在降低?
我们依旧假设有一个loss函数L,参数为w1,w2,即(w1,w2),现在我们要对原函数L的点(a,b)进行逼近,误差值为德尔塔x1=w1-a,德尔塔x2=w2-b,即x-x0
那么二阶展开式为
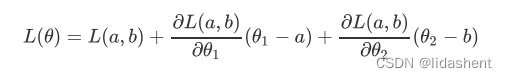
我们很容易知道他们的导数系数都是常量,常量我们直接可以简约化为uv,e在这里等于(德尔塔x1+德尔塔x2),因为x可能在x0左边或右边,而不会分布在两边,x的x1和x2分布在同一个范围内,那么我们简化为
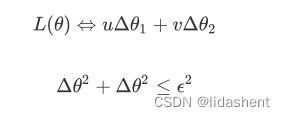
接下来该如何让通过更新德尔塔x1,德尔塔x2,让L降低呢?
我们可以使用向量算法,让(u,v)看做一个向量,(德尔塔x1,德尔塔x2)看做一个向量,
那么可以写为

接下来就到了让向量(u,v)与(德尔塔x1,德尔塔x2)得到最小值的环节,这样L就会降低了,那么怎么求向量的内积即乘积最小呢?
我们只需要取反方向即可,可以写为:
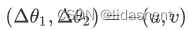
因为德尔塔x1和德尔塔x2是一个极小的与点x0的误差值,所以要给他加一个正数限制率
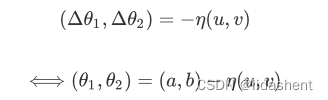
那么我们恢复之前的变换,可以清晰的看到
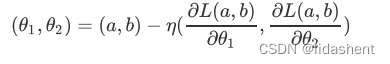
这正是我们在神经网络训练中,参数更新的方式,也就是导数或者梯度下降算法,随着训练的进行,梯度不断下降的同时,准确率在不断提升
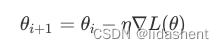
这就是使用梯度来作为参数更新的意义,直接在训练中提升准确率是虚无缥缈的,那么我们可以通过降低预测值和真实值的误差值来实现,
得到误差函数,只要我们不断的降低误差函数值预测值就在不断的提升,我们的训练目的就达到了
因此神经网络的主要基石就呼之欲出了
损失函数,优化算法,神经网络结构,这三板斧
当然,优良的数据也是重要的基石,因为数据决定了神经网络结果的上限,而训练神经网络只是让我们在不断逼近这个上限
动量算法
那么是否到此就万事大吉可以快乐的使用这个学习率的优化算法进行各种构建了呢?
他有一个巨大的问题,
我们假设loss函数长这样,把它想象成一个巨大的带有稍微坡度扁平的漏斗,他在水平方向上的坡度变化十分缓慢,在竖直方向上十分迅速
如果我们使用固定的学习率进行训练w,w落在这个盘面上Loss收敛将会极其缓慢,受制于学习率大小而且不能找到最优的w解

因此要让学习率根据梯度可变,让他自适应变化,总结来说就是当loss的梯度变化幅度小时,让学习率适当变大,让他训练的快一些
当loss的梯度变化幅度大时,让学习率适当变小,让他找到最优解.就是学习速度沿着loss图像直线时速度加快,沿着曲线方向时速度下降
看起来就像是一个球从高处滚下,要求他落到最低点,当坡度变化很小时他会逐渐加速,当出现一个小斜坡,坡度变化大时,他会逐渐减速,
我们对学习率进行一次改进,为其加入学习速度这一参数,w-v,v代表学习速度
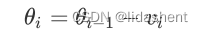
每次学习速度的更新都和上一次的梯度大小和方向有关,速度参数为y,小于1
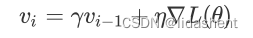
我们假设每次梯度更新都为g,
那么学习率速度变化就为,初始学习速度为0,y为小于0的数
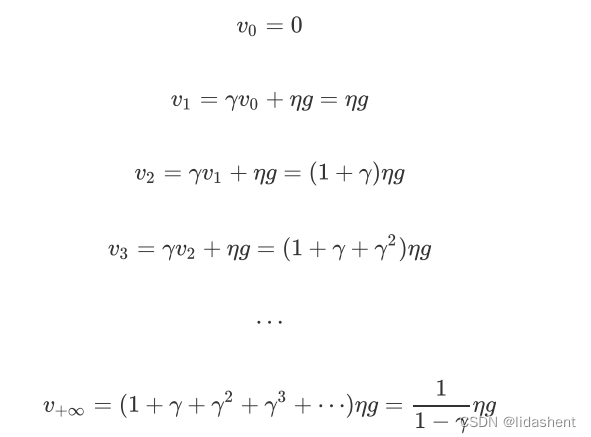
可以看到学习速度在不断提升,这个算法被称为自适应学习率算法,当y为0.5时,学习速度将会提升2倍
顺着这个思路向下延伸,为了找到loss函数的最低点,学习率在遇见最低点时应当进一步降低,最小化loss值
Adagrad 算法:
这个算法的想法是在训练每个批次的数据前,计算所有参数的学习率来为每个参数更新,其中每个参数的学习率都可以被表示为:
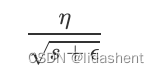
e为10^-10次方,是为了防止s为0
s则为当前参数每次梯度的平方和,即之前的梯度平方+现在的梯度平方累加到s上
这样当梯度变化小时,分数值将会变大,学习速率提升,当梯度变化大时,分数值变小,学习速率下降
它存在的一个问题是,因为梯度的平方和是持续累加的,最终必然导致学习率不断下降,甚至可能无法收敛
RMSProp算法:
为了避免s到后期太大以至于无法收敛的问题,人们提出了改进策略,对s的计算方式进行了改进
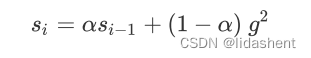
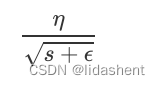
a被称为移动平均系数,这里a确保了s到后期不会太大
当然还有其他方式,比如
Adadelta算法
这种算法不需要设置学习率,而是根据梯度进行自动计算参数前进方向
先使用移动平均数来计算s
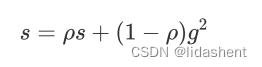
p和上面的a一样,g是参数当前梯度
计算参数更新变化量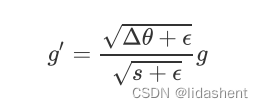
德尔塔w初始为0,做如下更新
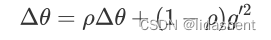
然后计算更新后的参数为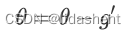
Adam 算法
它涉及的重要参数有一个变量动量v,一个移动指数加权平均s,一般预设B1=0.9,B2=0.999
初始值为0,每次迭代进行如下更新
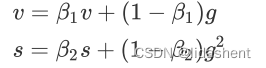
为了降低vs初期初始化为0的影响,每次vs都会做如下修正
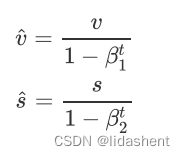
我们可以画出B1,B2的图像,以让我们明白此参数含义
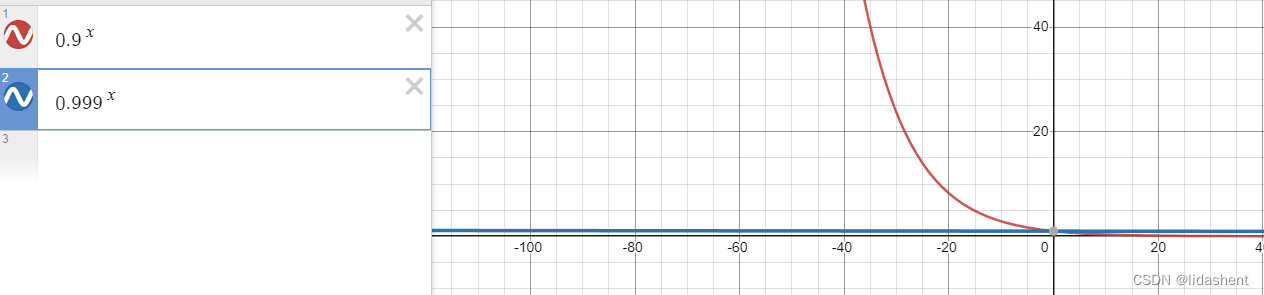
随着迭代次数t的增加,当0<=b1,b2<==1,后期其值约定于0,对vs影响不大,不会导致后期学习率急剧缩小无法收敛的问题
根据修正的vs重新计算学习率
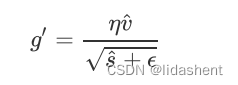
对参数更新
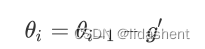
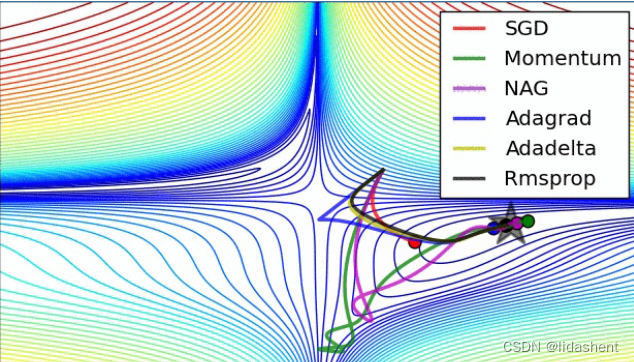
那么各个算法的优化效果到底如何呢,我们来看一下,红蓝代表loss函数高度的渐变
而实际上
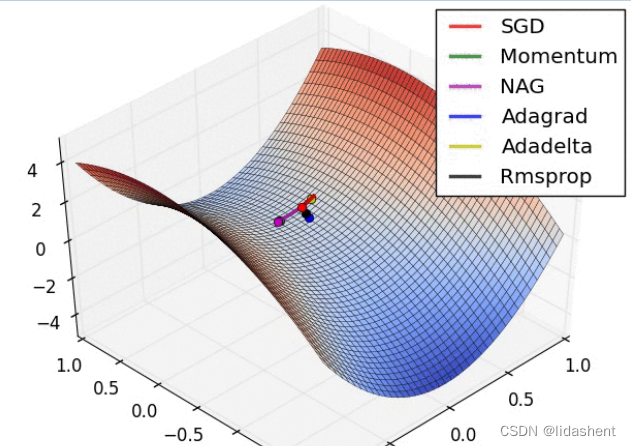
不过,这已经是不错的结果了
相关文章:

pytorch_神经网络构建2(数学原理)
文章目录 深层神经网络多分类深层网络反向传播算法优化算法动量算法Adam 算法 深层神经网络 分类基础理论: 交叉熵是信息论中用来衡量两个分布相似性的一种量化方式 之前讲述二分类的loss函数时我们使用公式-(y*log(y_)(1-y)*log(1-y_)进行误差计算 y表示真实值,y_表示预测值 …...
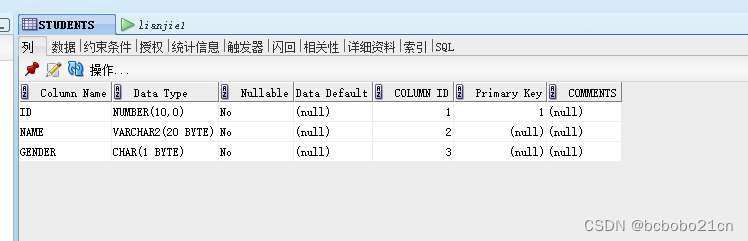
Oracle SQL Developer 中查看表的数据和字段属性、录入数据
在Oracle SQL Developer中,选中一个表时,右侧会列出表的情况;第一个tab是字段的名称、数据类型等属性; 切换到第二个tab,显示表的数据; 这和sql server management studio不一样的; 看一下部门…...

java docker图片叠加水印中文乱码
java docker图片叠加水印中文乱码 技术交流博客 http://idea.coderyj.com/ 1.由于项目需要后端需要叠加图片水印,但是中文乱码,导致叠加了之后 中文是框框 2.经过多方查找基本都说在 linux下安装字体就解决了,但是尝试了均无效 3.后来忽然想到我的项目是用docker打包部署的,不…...
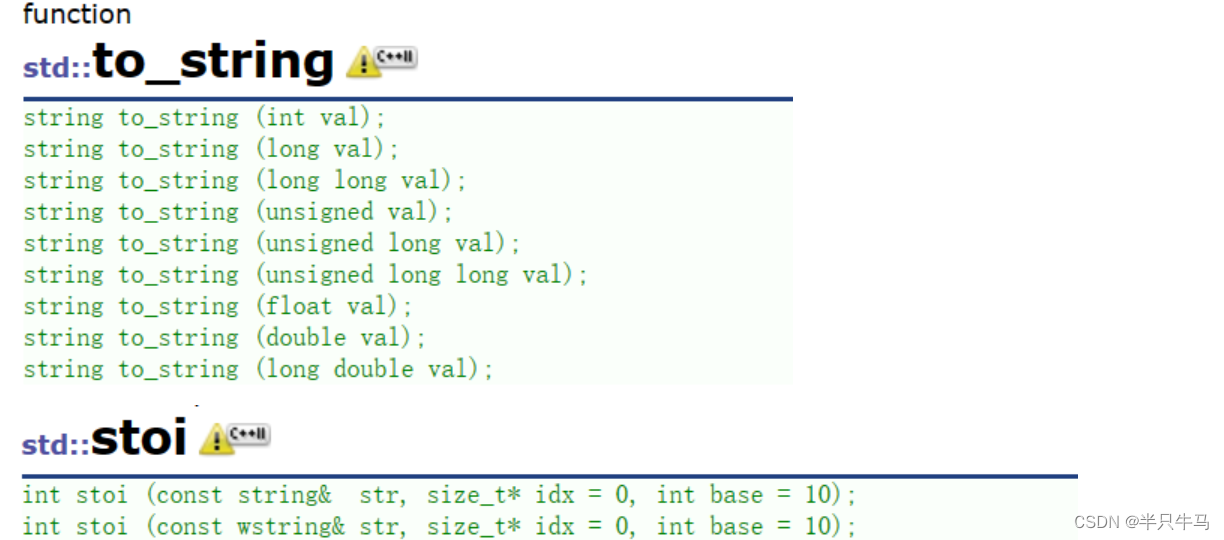
string类的使用方式的介绍
目录 前言 1.什么是STL 2. STL的版本 3. STL的六大组件 4.STL的缺陷 5.string 5.1 为什么学习string类? 5.1.1 C语言中的字符串 5.2 标准库中的string类 5.3 string类的常用接口的使用 5.3.1 构造函数 5.3.2 string类对象的容量操作 5.3.3 string类对象…...
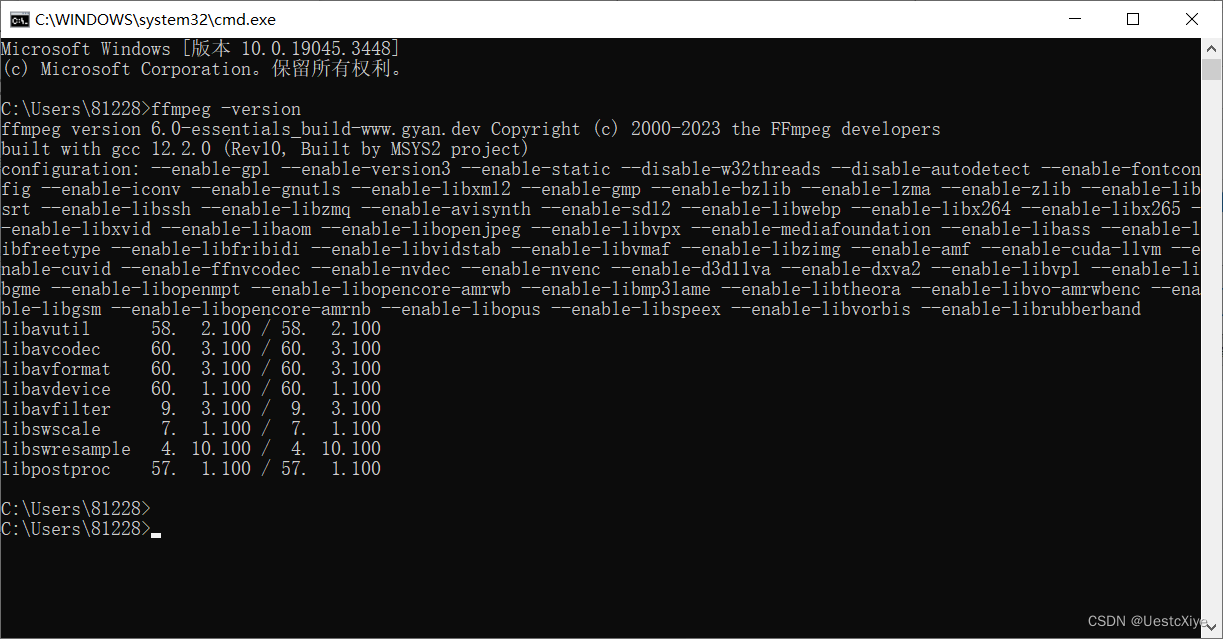
FFmpeg 命令:从入门到精通 | 命令行环境搭建
FFmpeg 命令:从入门到精通 | 命令行环境搭建 FFmpeg 命令:从入门到精通 | 命令行环境搭建安装 FFmpeg验证 FFmpeg 是否安装成功 FFmpeg 命令:从入门到精通 | 命令行环境搭建 安装 FFmpeg 进入 FFmpeg 官网: 点击 Download&#…...
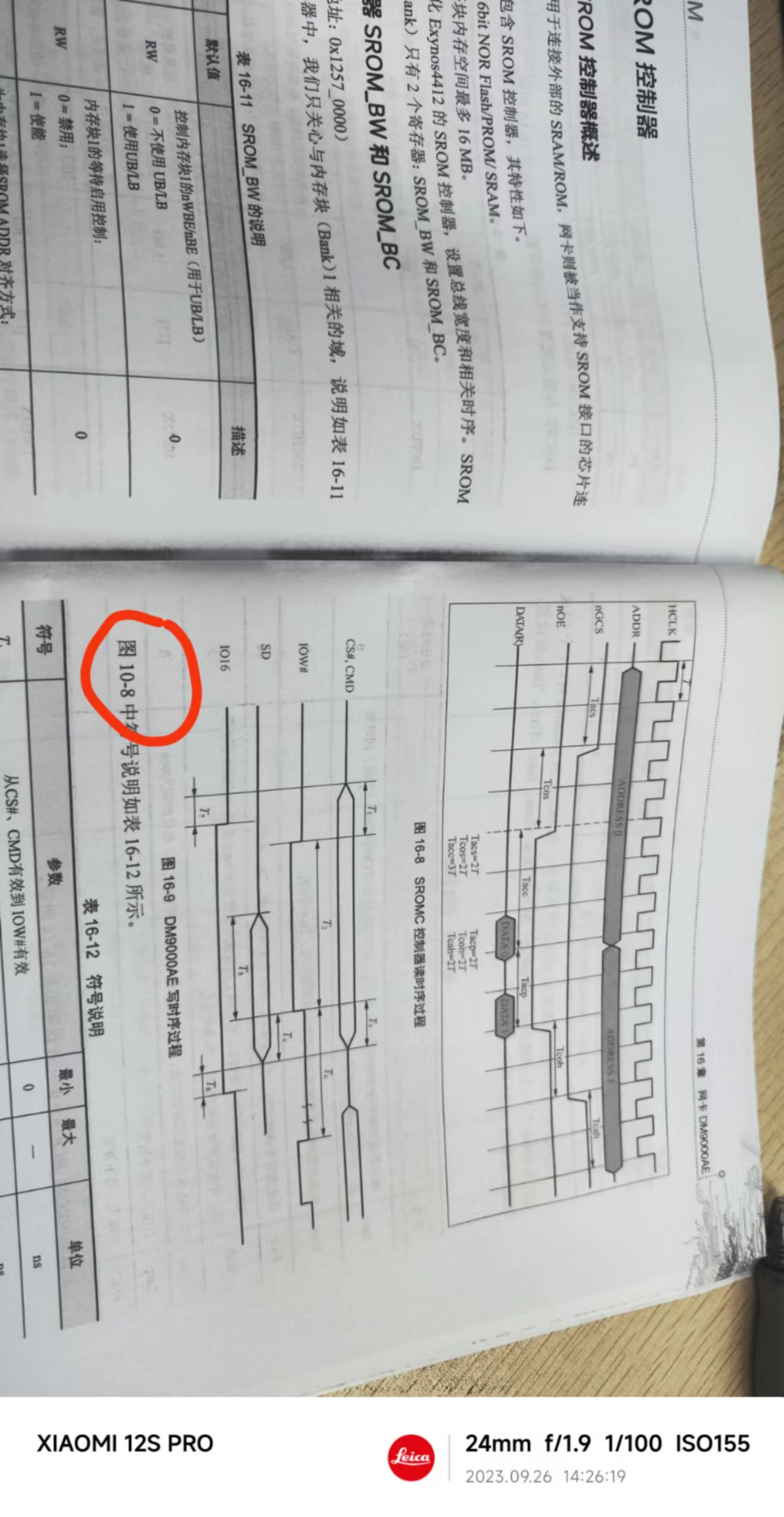
《从零开始学ARM》勘误
1. 50页 2 51页 3 236页 14.2.3 mkU-Boot 修改为: mkuboot 4 56页 修改为: 位[31:24]为条件标志位域,用f表示; 位[23:16]为状态位域,用s表示; 位[15:8]为扩展位域&…...

10款录屏软分析与选择使用,只看这篇文章就轻松搞定所有,高清4K无水印录屏,博主UP主轻松选择
录屏软件整理 如下为录屏软件,通过思维导图展示分析介绍: https://www.drawon.cn/template/details/6522bd5e0dad9029a0b528e1 如下为整理的录屏软件列表 名称产地价格支持的平台下载地址说明OBS国外免费开源windows/linux/machttps://obsproject.co…...
 -> listener.onItemClick(viewModel)}“)
android: android:onClick=“@{() -> listener.onItemClick(viewModel)}“
一、前言:在我使用editTest控件的时候,它的下方有一条横线。我想把它去掉然后我在布局文件中这样写 android:background"null" 导致报错,报错信息是: android:onClick"{() -> listener.onItemClick(viewModel)…...
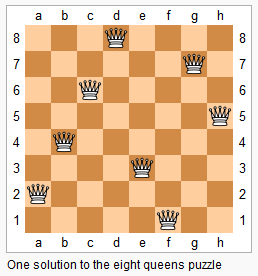
温故知新:dfs模板-843. n-皇后问题
n−n−皇后问题是指将 nn 个皇后放在 nnnn 的国际象棋棋盘上,使得皇后不能相互攻击到,即任意两个皇后都不能处于同一行、同一列或同一斜线上。 现在给定整数 nn,请你输出所有的满足条件的棋子摆法。 输入格式 共一行,包含整数 n…...

刷题笔记28——一直分不清的Kruskal、Prim、Dijkstra算法
图算法刷到这块,感觉像是走了一段黑路快回到家一样,看到这三个一直分不太清总是记混的名字,我满脑子想起的是大学数据结构课我坐在第一排,看着我班导一脸无奈,心想该怎么把这个知识点灌进木头脑袋里边呢。有很多算法我…...

Mysql时间同步设置
Mysql时间同步设置 当涉及到设置MySQL数据库时间与电脑同步时,实际的步骤可能会因操作系统和数据库版本的不同而有所差异。以下是一个基本的步骤示例,供您参考: 检查电脑时间: 首先确保电脑操作系统的时间是正确的。 设置MySQL时…...
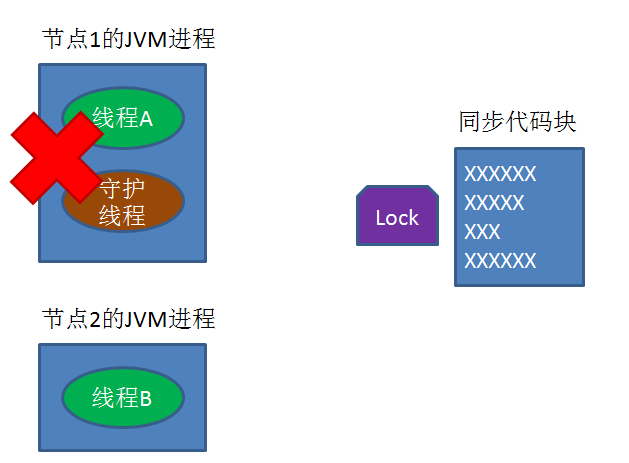
如何理解分布式锁?
分布式锁的实现有哪些? 1.Memcached分布式锁 利用Memcached的add命令。此命令是原子操作,只有在key不存在的情况下,才能add成功,也就意味着线程得到了锁。 2.Reids分布式锁 和Memcached的方式类似,利用Redis的setn…...
windows 远程连接 ubuntu桌面xrdp
更新 sudo apt update安装组件 sudo apt-get install xorg sudo apt-get install xserver-xorg-core sudo apt-get install xorgxrdp sudo apt install xfce4 xfce4-goodies xorg dbus-x11 x11-xserver-utilsxrdp sudo apt install xrdp sudo systemctl status xrdp sudo …...

数据采集时使用HTTP代理IP效率不高怎么办?
在进行数据采集时,使用HTTP代理 可以帮助我们实现隐私保护和规避封禁的目的。然而,有时候我们可能会遇到使用HTTP代理 效率不高的问题,如连接延迟、速度慢等。本文将为您分享解决这一问题的实用技巧,帮助您提高数据采集效率&#…...
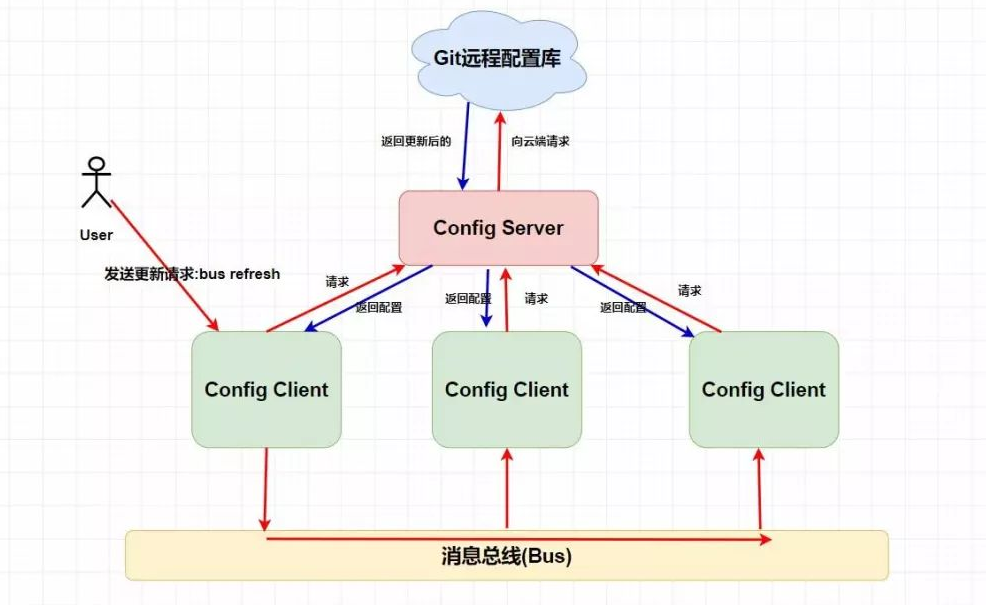
你了解的SpringCloud核心组件有哪些?他们各有什么作用?
SpringCloud 1.什么是 Spring cloud Spring Cloud 为最常见的分布式系统模式提供了一种简单且易于接受的编程模型,帮助开发人员构建有弹性的、可靠的、协调的应用程序。Spring Cloud 构建于 Spring Boot 之上,使得开发者很容易入手并快速应用于生产中。…...

【Gradle-10】不可忽视的构建分析
1、前言 构建性能对于生产力至关重要。 随着项目越来越复杂,花费在构建上的时间就越长,开发效率就越低。 通过分析构建过程,可以了解项目构建的时间都花在哪,以及项目存在哪些潜在的问题,找到构建瓶颈,解…...

2034. 股票价格波动
给你一支股票价格的数据流。数据流中每一条记录包含一个 时间戳 和该时间点股票对应的 价格 。 不巧的是,由于股票市场内在的波动性,股票价格记录可能不是按时间顺序到来的。某些情况下,有的记录可能是错的。如果两个有相同时间戳的记录出现…...

JavaScript 事件详解细节
JavaScript 事件详解细节 JavaScript 中的事件是前端开发中非常重要的一个概念。通过事件,我们可以捕捉和响应用户与网页的交互,比如点击按钮、输入文字等。这篇博客文章将详细介绍 JavaScript 中的事件,希望能帮助你更好地理解和使用这一功…...
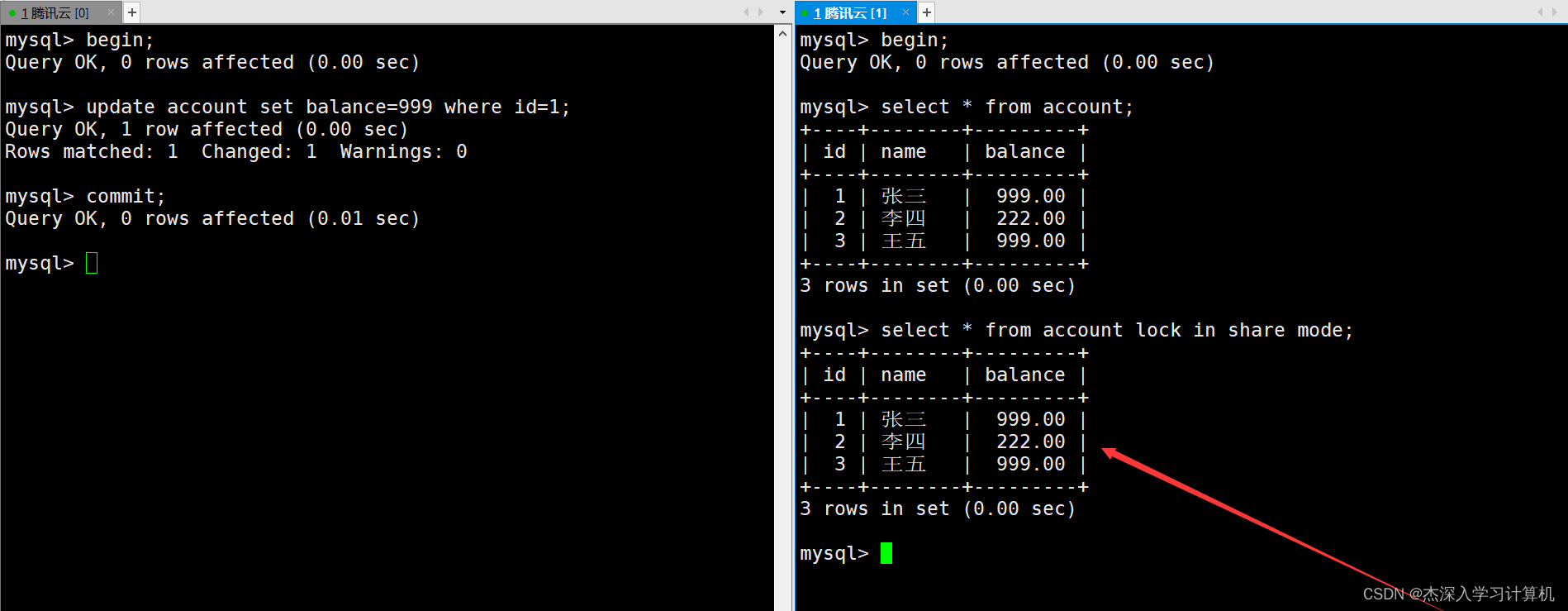
【MySQL】事务管理
目录 MySQL事务管理 事务的概念 事务的版本支持 事务的提交方式 事务的相关演示 事务的隔离级别 查看与设置隔离级别 读未提交(Read Uncommitted) 读提交(Read Committed) 可重复读(Repeatable Read…...

Git 学习笔记 | Git 基本操作命令
Git 学习笔记 | Git 基本操作命令 Git 学习笔记 | Git 基本操作命令文件的四种状态查看文件状态忽略文件 Git 学习笔记 | Git 基本操作命令 文件的四种状态 版本控制就是对文件的版本控制,要对文件进行修改、提交等操作,首先要知道文件当前在什么状态&…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

Vue 实例的数据对象详解
Vue 实例的数据对象详解 在 Vue 中,数据对象是响应式系统的核心,也是组件状态的载体。理解数据对象的原理和使用方式是成为 Vue 专家的关键一步。我将从多个维度深入剖析 Vue 实例的数据对象。 一、数据对象的定义方式 1. Options API 中的定义 在 Options API 中,使用 …...
