【学习笔记】莫比乌斯反演
退役OIer回来受虐啦
一些定义
μ ( x ) = { 1 x > 1 ( − 1 ) n x = ∏ i = 1 n P i 0 o t h e r w i s e \mu(x) = \begin{cases} 1 & x > 1 \\ (-1)^n & x = \prod _ {i=1} ^ {n} P_{i}\\ 0 & otherwise \end{cases} μ(x)=⎩ ⎨ ⎧1(−1)n0x>1x=∏i=1nPiotherwise
φ ( n ) = ∑ i = 1 n [ g c d ( i , n ) = 1 ] \varphi(n)=\sum_{i=1}^{n}\ [gcd(i,n)=1] φ(n)=i=1∑n [gcd(i,n)=1]
ε ( n ) = [ n = 1 ] \varepsilon(n)=\ [n=1] ε(n)= [n=1]
一些性质
∑ d ∣ n μ ( d ) = ε ( n ) \sum_{d|n}\mu(d)=\varepsilon(n) d∣n∑μ(d)=ε(n)
即 μ ∗ 1 = ε \mu\ast1=\varepsilon μ∗1=ε
推广一下:
[ g c d ( i , j ) = 1 ] = ∑ d ∣ g c d ( i , j ) μ ( d ) [gcd(i,j)=1]=\sum_{d|gcd(i,j)}\mu(d) [gcd(i,j)=1]=d∣gcd(i,j)∑μ(d)
φ ∗ 1 = i d \varphi \ast 1=id φ∗1=id
莫比乌斯变换
f ( n ) = ∑ d ∣ n g ( d ) ⇒ g ( n ) = ∑ d ∣ n f ( d ) μ ( n d ) f(n)=\sum_{d|n} g(d)\ \Rightarrow\ g(n)=\sum_{d|n}f(d)\mu(\frac{n}{d}) f(n)=d∣n∑g(d) ⇒ g(n)=d∣n∑f(d)μ(dn)
f ( n ) = ∑ n ∣ d g ( d ) ⇒ g ( n ) = ∑ n ∣ d μ ( d n ) f ( d ) f(n)=\sum_{n|d}g(d)\ \Rightarrow\ g(n)=\sum_{n|d}\mu(\frac{d}{n})f(d) f(n)=n∣d∑g(d) ⇒ g(n)=n∣d∑μ(nd)f(d)
例题
[HAOI2011] Problem b
题目描述
对于给出的 n n n 个询问,每次求有多少个数对 ( x , y ) (x,y) (x,y),满足 a ≤ x ≤ b a \le x \le b a≤x≤b, c ≤ y ≤ d c \le y \le d c≤y≤d,且 gcd ( x , y ) = k \gcd(x,y) = k gcd(x,y)=k, gcd ( x , y ) \gcd(x,y) gcd(x,y) 函数为 x x x 和 y y y 的最大公约数。
输入格式
第一行一个整数 n n n,接下来 n n n 行每行五个整数,分别表示 a , b , c , d , k a,b,c,d,k a,b,c,d,k。
输出格式
共 n n n 行,每行一个整数表示满足要求的数对 ( x , y ) (x,y) (x,y) 的个数。
样例 #1
样例输入 #1
2
2 5 1 5 1
1 5 1 5 2
样例输出 #1
14
3
提示
对于 100 % 100\% 100% 的数据满足: 1 ≤ n , k ≤ 5 × 1 0 4 1 \le n,k \le 5 \times 10^4 1≤n,k≤5×104, 1 ≤ a ≤ b ≤ 5 × 1 0 4 1 \le a \le b \le 5 \times 10^4 1≤a≤b≤5×104, 1 ≤ c ≤ d ≤ 5 × 1 0 4 1 \le c \le d \le 5 \times 10^4 1≤c≤d≤5×104。
题解
根据容斥原理,原式可以分成 4 块来处理,每一块的式子都为
∑ i = 1 n ∑ j = 1 m [ gcd ( i , j ) = k ] \sum_{i=1}^{n}\sum_{j=1}^{m}[\gcd(i,j)=k] i=1∑nj=1∑m[gcd(i,j)=k]
考虑化简该式子
∑ i = 1 ⌊ n k ⌋ ∑ j = 1 ⌊ m k ⌋ ε ( gcd ( i , j ) ) \sum_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{k}\rfloor}\varepsilon(\gcd(i,j)) i=1∑⌊kn⌋j=1∑⌊km⌋ε(gcd(i,j))
将 ε \varepsilon ε 函数展开得到
∑ i = 1 ⌊ n k ⌋ ∑ j = 1 ⌊ m k ⌋ ∑ d ∣ gcd ( i , j ) μ ( d ) \displaystyle\sum_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{k}\rfloor}\sum_{d\mid \gcd(i,j)}\mu(d) i=1∑⌊kn⌋j=1∑⌊km⌋d∣gcd(i,j)∑μ(d)
变换求和顺序,先枚举 d ∣ gcd ( i , j ) d\mid \gcd(i,j) d∣gcd(i,j) 可得
∑ d = 1 μ ( d ) ∑ i = 1 ⌊ n k ⌋ [ d ∣ i ] ∑ j = 1 ⌊ m k ⌋ [ d ∣ j ] \displaystyle\sum_{d=1}\mu(d)\sum_{i=1}^{\lfloor\frac{n}{k}\rfloor}[d\mid i]\sum_{j=1}^{\lfloor\frac{m}{k}\rfloor}[d\mid j] d=1∑μ(d)i=1∑⌊kn⌋[d∣i]j=1∑⌊km⌋[d∣j]
易知 1 ∼ ⌊ n k ⌋ 1\sim\lfloor\dfrac{n}{k}\rfloor 1∼⌊kn⌋ 中 d d d 的倍数有 ⌊ n k d ⌋ \lfloor\dfrac{n}{kd}\rfloor ⌊kdn⌋ 个,故原式化为
∑ d = 1 min ( ⌊ n k ⌋ , ⌊ m k ⌋ ) μ ( d ) ⌊ n k d ⌋ ⌊ m k d ⌋ \displaystyle\sum_{d=1}^{\min(\lfloor \frac{n}{k}\rfloor,\lfloor \frac{m}{k}\rfloor)}\mu(d)\lfloor\frac{n}{kd}\rfloor\lfloor\frac{m}{kd}\rfloor d=1∑min(⌊kn⌋,⌊km⌋)μ(d)⌊kdn⌋⌊kdm⌋
整除分块即可求解
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+77;
int mu[N],sum[N];
vector<int> p;
bool bz[N];
void init(int n)
{mu[1]=1;for(int i=2; i<=n; i++){if(!bz[i]){mu[i]=-1;p.push_back(i);}for(auto j:p){if(j*i>n) break;bz[i*j]=1;if(i%j==0) break;else mu[i*j]=-mu[i];}}for(int i=1; i<=n; i++) sum[i]=sum[i-1]+mu[i];
}
int solve(int n,int m,int k)
{int ans=0;n/=k; m/=k;for(int l=1,r; l<=min(n,m); l=r+1){r=min((n/(n/l)),(m/(m/l)));ans+=(n/l)*(m/l)*(sum[r]-sum[l-1]);}return ans;
}
void O_o()
{int a,b,c,d,k;cin>>a>>b>>c>>d>>k;cout<<solve(b,d,k)-solve(a-1,d,k)-solve(b,c-1,k)+solve(a-1,c-1,k)<<"\n";
}
signed main()
{ios::sync_with_stdio(false); cin.tie(0),cout.tie(0);int T=1;init(50000);cin>>T;while(T--){O_o();}
}
[国家集训队] Crash的数字表格 / JZPTAB
题目描述
今天的数学课上,Crash 小朋友学习了最小公倍数(Least Common Multiple)。对于两个正整数 a a a 和 b b b, lcm ( a , b ) \text{lcm}(a,b) lcm(a,b) 表示能同时被 a a a 和 b b b 整除的最小正整数。例如, lcm ( 6 , 8 ) = 24 \text{lcm}(6, 8) = 24 lcm(6,8)=24。
回到家后,Crash 还在想着课上学的东西,为了研究最小公倍数,他画了一张 $ n \times m$ 的表格。每个格子里写了一个数字,其中第 i i i 行第 j j j 列的那个格子里写着数为 lcm ( i , j ) \text{lcm}(i, j) lcm(i,j)。
看着这个表格,Crash 想到了很多可以思考的问题。不过他最想解决的问题却是一个十分简单的问题:这个表格中所有数的和是多少。当 n n n 和 m m m 很大时,Crash 就束手无策了,因此他找到了聪明的你用程序帮他解决这个问题。由于最终结果可能会很大,Crash 只想知道表格里所有数的和对 20101009 20101009 20101009 取模后的值。
输入格式
输入包含一行两个整数,分别表示 n n n 和 m m m。
输出格式
输出一个正整数,表示表格中所有数的和对 20101009 20101009 20101009 取模后的值。
样例 #1
样例输入 #1
4 5
样例输出 #1
122
提示
样例输入输出 1 解释
该表格为:
| 1 1 1 | 2 2 2 | 3 3 3 | 4 4 4 | 5 5 5 |
|---|---|---|---|---|
| 2 2 2 | 2 2 2 | 6 6 6 | 4 4 4 | 10 10 10 |
| 3 3 3 | 6 6 6 | 3 3 3 | 12 12 12 | 15 15 15 |
| 4 4 4 | 4 4 4 | 12 12 12 | 4 4 4 | 20 20 20 |
数据规模与约定
- 对于 30 % 30\% 30% 的数据,保证 n , m ≤ 1 0 3 n, m \le 10^3 n,m≤103。
- 对于 70 % 70\% 70% 的数据,保证 n , m ≤ 1 0 5 n, m \le 10^5 n,m≤105。
- 对于 100 % 100\% 100% 的数据,保证 1 ≤ n , m ≤ 1 0 7 1\le n,m \le 10^7 1≤n,m≤107。
题解
∑ i = 1 n ∑ j = 1 m l c m ( i , j ) = ∑ i = 1 n ∑ j = 1 m i ⋅ j g c d ( i , j ) = ∑ i = 1 n ∑ j = 1 m ∑ d = g c d ( i , j ) i ⋅ j d = ∑ d = 1 m i n ( n , m ) ∑ d ∣ i n ∑ d ∣ j m [ g c d ( i , j ) = d ] i ⋅ j d = ∑ d = 1 m i n ( n , m ) d ∑ i = 1 ⌊ n d ⌋ ∑ j = 1 ⌊ m d ⌋ [ g c d ( i , j ) = 1 ] i j \sum_{i=1}^{n}\sum_{j=1}^{m} lcm(i,j)\\ =\sum_{i=1}^{n}\sum_{j=1}^{m} \frac{i\cdot j}{gcd(i,j)}\\ =\sum_{i=1}^{n}\sum_{j=1}^{m}\sum_{d=gcd(i,j)} \frac{i\cdot j}{d}\\ =\sum_{d=1}^{min(n,m)}\sum_{d|i}^{n}\sum_{d|j}^{m} [gcd(i,j)=d]\frac{i\cdot j}{d}\\ =\sum_{d=1}^{min(n,m)}d\ \sum_{i=1}^{\left\lfloor \frac{n}{d} \right\rfloor}\sum_{j=1}^{\left\lfloor \frac{m}{d} \right\rfloor} [gcd(i,j)=1]i j i=1∑nj=1∑mlcm(i,j)=i=1∑nj=1∑mgcd(i,j)i⋅j=i=1∑nj=1∑md=gcd(i,j)∑di⋅j=d=1∑min(n,m)d∣i∑nd∣j∑m[gcd(i,j)=d]di⋅j=d=1∑min(n,m)d i=1∑⌊dn⌋j=1∑⌊dm⌋[gcd(i,j)=1]ij
令 S ( n , m ) = ∑ i = 1 n ∑ j = 1 m [ g c d ( i , j ) = 1 ] i j S(n,m)=\sum_{i=1}^{n}\sum_{j=1}^{m} [gcd(i,j)=1]i j S(n,m)=∑i=1n∑j=1m[gcd(i,j)=1]ij
S ( n , m ) = ∑ i = 1 n ∑ j = 1 m [ g c d ( i , j ) = 1 ] i j = ∑ d = 1 n ∑ d ∣ i n ∑ d ∣ j m μ ( d ) ⋅ i ⋅ j = ∑ d = 1 n μ ( d ) ⋅ d 2 ⋅ ∑ i = 1 ⌊ n d ⌋ ∑ j = 1 ⌊ m d ⌋ i ⋅ j S(n,m)=\sum_{i=1}^{n}\sum_{j=1}^{m} [gcd(i,j)=1]i j\\ =\sum_{d=1}^n\sum_{d\mid i}^n\sum_{d\mid j}^m\mu(d)\cdot i\cdot j\\ =\sum_{d=1}^n\mu(d)\cdot d^2\cdot\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}i\cdot j S(n,m)=i=1∑nj=1∑m[gcd(i,j)=1]ij=d=1∑nd∣i∑nd∣j∑mμ(d)⋅i⋅j=d=1∑nμ(d)⋅d2⋅i=1∑⌊dn⌋j=1∑⌊dm⌋i⋅j
观察上式,前半段可以预处理前缀和;后半段又是一个范围内数对之和,记
g ( n , m ) = ∑ i = 1 n ∑ j = 1 m i ⋅ j = n ⋅ ( n + 1 ) 2 × m ⋅ ( m + 1 ) 2 g(n,m)=\sum_{i=1}^n\sum_{j=1}^m i\cdot j=\frac{n\cdot(n+1)}{2}\times\frac{m\cdot(m+1)}{2} g(n,m)=i=1∑nj=1∑mi⋅j=2n⋅(n+1)×2m⋅(m+1)
可以 Θ ( 1 ) \Theta(1) Θ(1) 求解
不过这玩意要整除分块套整除分块,而且细节不少
代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e7+7,mod=20101009;
int mu[N],sum[N];
vector<int> p;
bool bz[N];
int Sum(int x, int y)
{return ((x*(x+1)/2%mod)*(y*(y+1)/2%mod))%mod;
}
void init(int n)
{mu[1]=1;for(int i=2; i<=n; i++){if(!bz[i]){mu[i]=-1;p.push_back(i);}for(auto j:p){if(j*i>n) break;bz[i*j]=1;if(i%j==0) break;else mu[i*j]=-mu[i];}}for(int i=1; i<=n; i++) sum[i]=(sum[i-1]+mu[i]*i*i%mod)%mod;
}
int S(int n,int m)
{int ans=0;for(int l=1,r; l<=min(n,m); l=r+1){r=min(n/(n/l),m/(m/l));(ans+=Sum(n/l,m/l)%mod*(sum[r]-sum[l-1])%mod)%=mod;}return ans;
}
void O_o()
{int n,m,ans=0;cin>>n>>m;init(n);for(int l=1,r; l<=min(n,m); l=r+1){r=min(n/(n/l),m/(m/l));(ans+=((r-l+1)*(l+r)/2)%mod*S(n/l,m/l)%mod)%=mod;}cout<<(ans+mod)%mod;
}
signed main()
{ios::sync_with_stdio(false); cin.tie(0),cout.tie(0);int T=1;// cin>>T;while(T--){O_o();}
}
相关文章:

【学习笔记】莫比乌斯反演
退役OIer回来受虐啦 一些定义 μ ( x ) { 1 x > 1 ( − 1 ) n x ∏ i 1 n P i 0 o t h e r w i s e \mu(x) \begin{cases} 1 & x > 1 \\ (-1)^n & x \prod _ {i1} ^ {n} P_{i}\\ 0 & otherwise \end{cases} μ(x)⎩ ⎨ ⎧1(−1)n0x>1x∏i1nPi…...

一款构建Python命令行应用的开源库
1 简介 当我们编写 Python 程序时,我们经常需要与用户进行交互,接收输入并输出结果。Python 提供了许多方法来实现这一点,其中一个非常方便的方法是使用 typer 库。typer 是一个用于构建命令行应用程序的 Python 库,它使得创建命令…...

10-Node.js模块化
01.模块化简介 目标 了解模块化概念和好处,以及 CommonJS 标准语法导出和导入 讲解 在 Node.js 中每个文件都被当做是一个独立的模块,模块内定义的变量和函数都是独立作用域的,因为 Node.js 在执行模块代码时,将使用如下所示的…...

数字IC前端学习笔记:数字乘法器的优化设计(Dadda Tree乘法器)
相关阅读 数字IC前端https://blog.csdn.net/weixin_45791458/category_12173698.html?spm1001.2014.3001.5482 华莱士树仍然是一种比较规则的结构(这使得可以方便地生成树的结构),这导致了它所使用的全加器和半加器个数不是最少的ÿ…...

计算机专业毕业设计项目推荐14-文档编辑平台(SpringBoot+Vue+Mysql)
文档编辑平台(SpringBootVueMysql) **介绍****各部分模块实现** 介绍 本系列(后期可能博主会统一为专栏)博文献给即将毕业的计算机专业同学们,因为博主自身本科和硕士也是科班出生,所以也比较了解计算机专业的毕业设计流程以及模式,在编写的…...
)
【读书后台管理系统】—后端框架搭建(二)
【读书后台管理系统】—后端框架搭建(二) 一、 Node 简介 Node 是一个基于 V8 引擎的 Javascript 运行环境,它使得 Javascript 可以运行在服务端,直接与操作系统进行交互,与文件控制、网络交互、进程控制等 Chrome …...
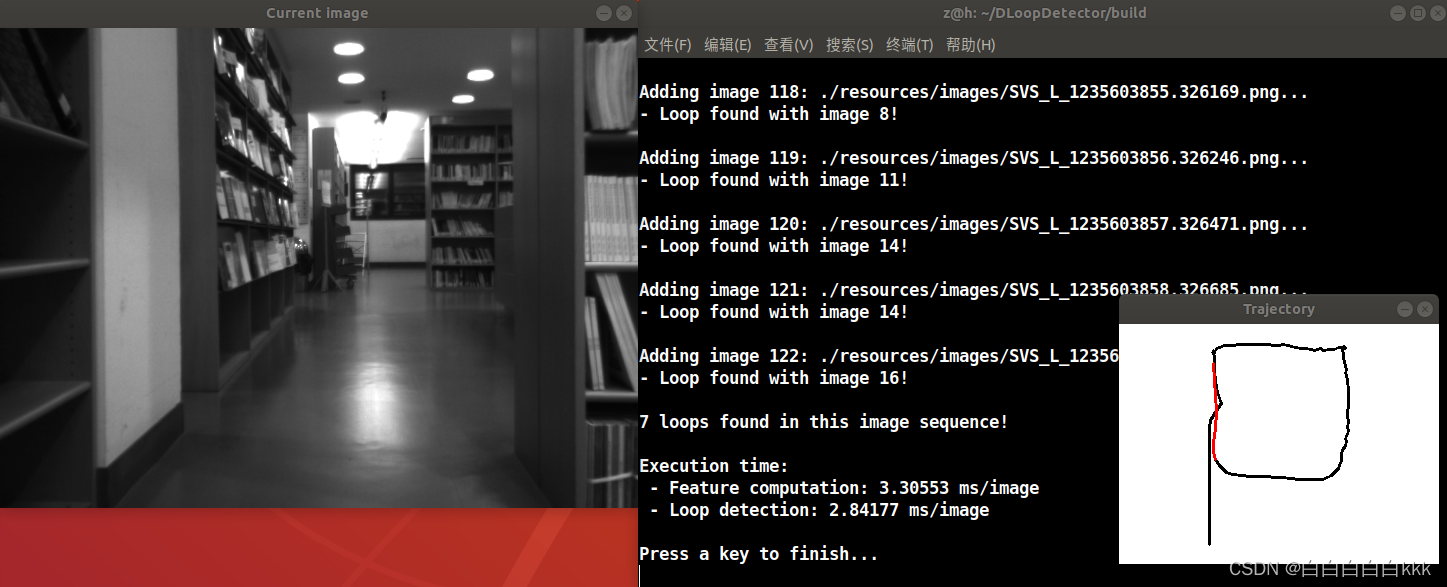
【DLoopDetector(C++)】DBow2词袋模型loop close学习
0.前言 最近读了两篇论文,论文作者开源了一种基于词袋模型DBoW2库的DLoopDetector算法,自己运行demo测试一下 对应论文介绍:Bags of Binary Words for Fast Place Recognition in Image Sequences 开源项目Github地址:https://gi…...
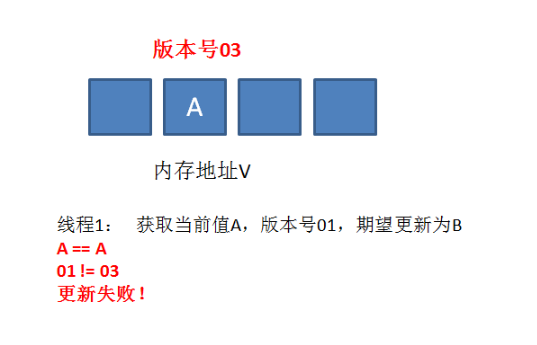
什么是CAS机制?
CAS和Synchronized的区别是什么?适合什么样的场景?有什么样的优点和缺点? 示例程序:启动两个线程,每个线程中让静态变量count循环累加100次。 public class ThreadTest {private static int count 0;public static …...

Java多态详解
下面讲解一下Java中的多态机制,力求用最通俗易懂的语言,最精炼的话语,最生动的例子,深入浅出Java多态,帮助读者轻松掌握这个知识点。 什么是多态? 多态是指同一种行为具有多个不同表现形式的能力。 多态…...

Android中简单实现Spinner的数据绑定
Android中简单实现Spinner的数据绑定 然后声明对象实例并加入到arraylist里面,并设置spinner的适配器 Spinner Sp (Spinner).............// List<CItem > lst new ArrayList<CItem>(); CItem ct new CItem ("1","测试"); lst.Add(ct)…...
【版本控制工具二】Git 和 Gitee 建立联系
文章目录 前言一、Git 和 Gitee 建立联系1.1 任意目录下,打开 git bash 命令行,输入以下命令生成公钥1.2 配置SSH公钥1.3 进行全局配置 二、其它相关Git指令2.1 常用指令2.2 指令操作可能出现的问题 三、补充3.1 **为什么要先commit,然后pull…...

最新AI智能创作系统ChatGPT商业源码+详细图文搭建部署教程+AI绘画系统
一、AI系统介绍 SparkAi创作系统是基于国外很火的ChatGPT进行开发的Ai智能问答系统。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI创作ChatGPT?小编这里写一个详细图文教程吧&am…...

【算法与数据结构】--目录
第一部分:算法基础 第一章:算法入门第二章:数据结构概述第三章:算法设计与分析 3.1 贪心算法3.2 动态规划3.3 分治算法3.4 回溯算法 第二部分:常见数据结构 第四章:数组和链表 4.1 数组4.2 链表4.3 比较…...

爱普生LQ1900KIIH复位方法
爱普生EPSON 1900KIIH是一部通用针式打印机,136列(10cpi下)的打印宽度,缓冲区128KB,打印速度为270字/秒。 打印机类型 打印方式:24针击打式点阵打印、打印方向:双向逻辑查找、安全规格标准&am…...
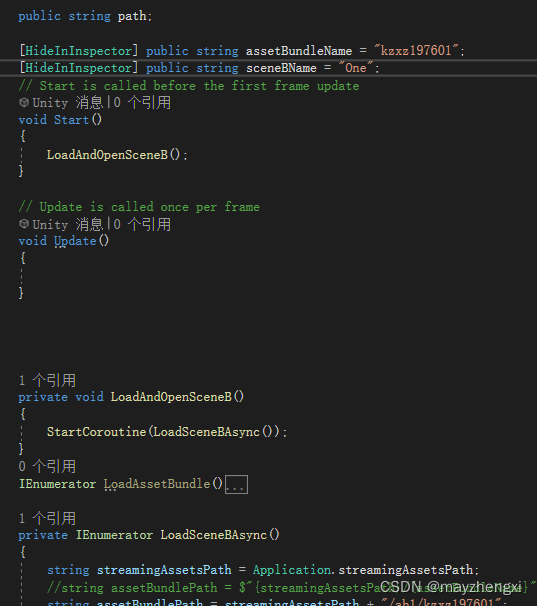
字段位置顺序对值的影响
Unity中验证AB加载场景时报错: Cannot load scene: Invalid scene name (empty string) and invalid build index -1 报错原因是因为把字段放在了Start函数后面(图一)改成(图二)就好了。图一中协程使用的sceneBName字段值为null。 图一: 图二:…...
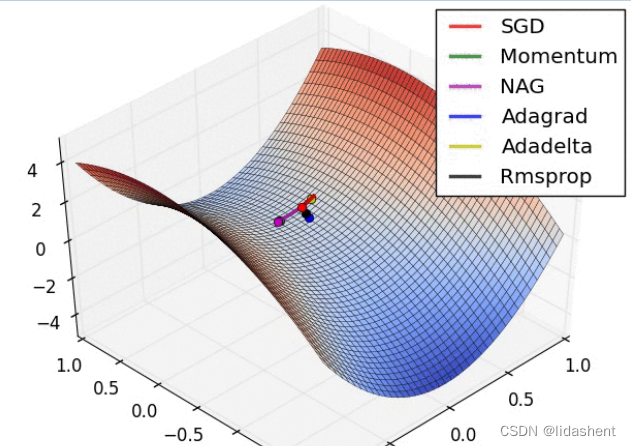
pytorch_神经网络构建2(数学原理)
文章目录 深层神经网络多分类深层网络反向传播算法优化算法动量算法Adam 算法 深层神经网络 分类基础理论: 交叉熵是信息论中用来衡量两个分布相似性的一种量化方式 之前讲述二分类的loss函数时我们使用公式-(y*log(y_)(1-y)*log(1-y_)进行误差计算 y表示真实值,y_表示预测值 …...
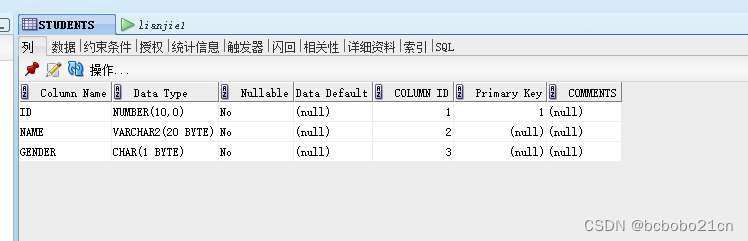
Oracle SQL Developer 中查看表的数据和字段属性、录入数据
在Oracle SQL Developer中,选中一个表时,右侧会列出表的情况;第一个tab是字段的名称、数据类型等属性; 切换到第二个tab,显示表的数据; 这和sql server management studio不一样的; 看一下部门…...

java docker图片叠加水印中文乱码
java docker图片叠加水印中文乱码 技术交流博客 http://idea.coderyj.com/ 1.由于项目需要后端需要叠加图片水印,但是中文乱码,导致叠加了之后 中文是框框 2.经过多方查找基本都说在 linux下安装字体就解决了,但是尝试了均无效 3.后来忽然想到我的项目是用docker打包部署的,不…...
string类的使用方式的介绍
目录 前言 1.什么是STL 2. STL的版本 3. STL的六大组件 4.STL的缺陷 5.string 5.1 为什么学习string类? 5.1.1 C语言中的字符串 5.2 标准库中的string类 5.3 string类的常用接口的使用 5.3.1 构造函数 5.3.2 string类对象的容量操作 5.3.3 string类对象…...
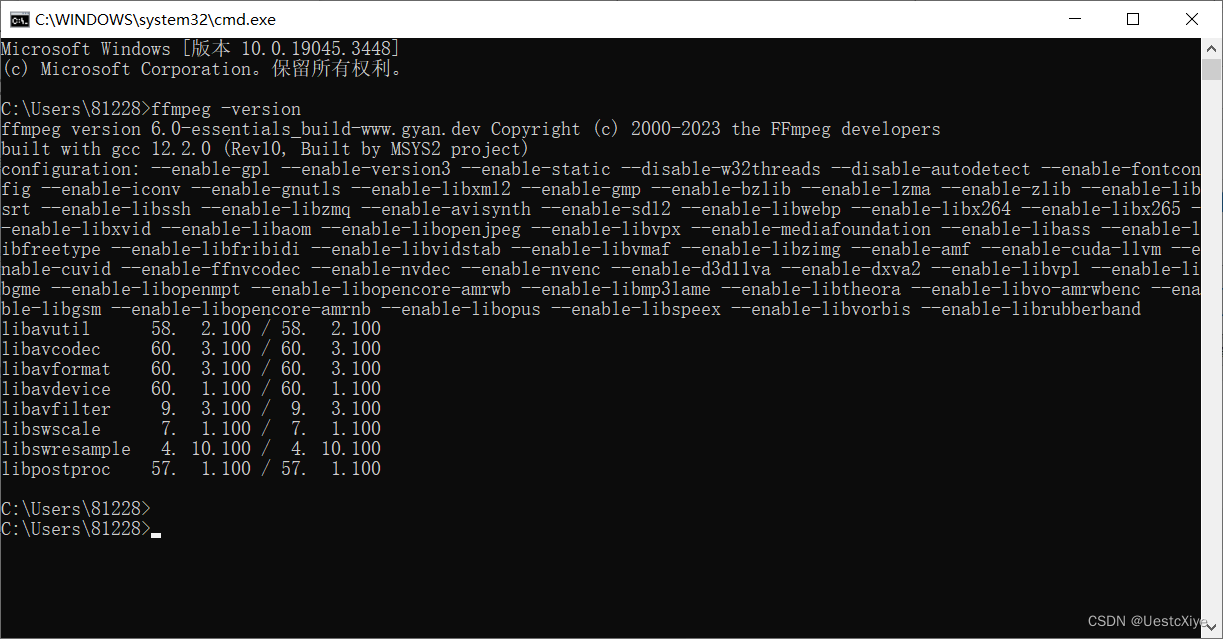
FFmpeg 命令:从入门到精通 | 命令行环境搭建
FFmpeg 命令:从入门到精通 | 命令行环境搭建 FFmpeg 命令:从入门到精通 | 命令行环境搭建安装 FFmpeg验证 FFmpeg 是否安装成功 FFmpeg 命令:从入门到精通 | 命令行环境搭建 安装 FFmpeg 进入 FFmpeg 官网: 点击 Download&#…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...
