【数据结构-二叉树 八】【遍历求和】:求根到叶子节点数字之和
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【遍历求和】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为:目标公司+最近一年+出现频率排序,由高到低的去牛客TOP101去找,只有两个地方都出现过才做这道题(CodeTop本身汇聚了LeetCode的来源),确保刷的题都是高频要面试考的题。
明确目标题后,附上题目链接,后期可以依据解题思路反复快速练习,题目按照题干的基本数据结构分类,且每个分类的第一篇必定是对基础数据结构的介绍。
求根到叶子节点数字之和【MID】
DFS和BFS两种做法
题干
直接粘题干和用例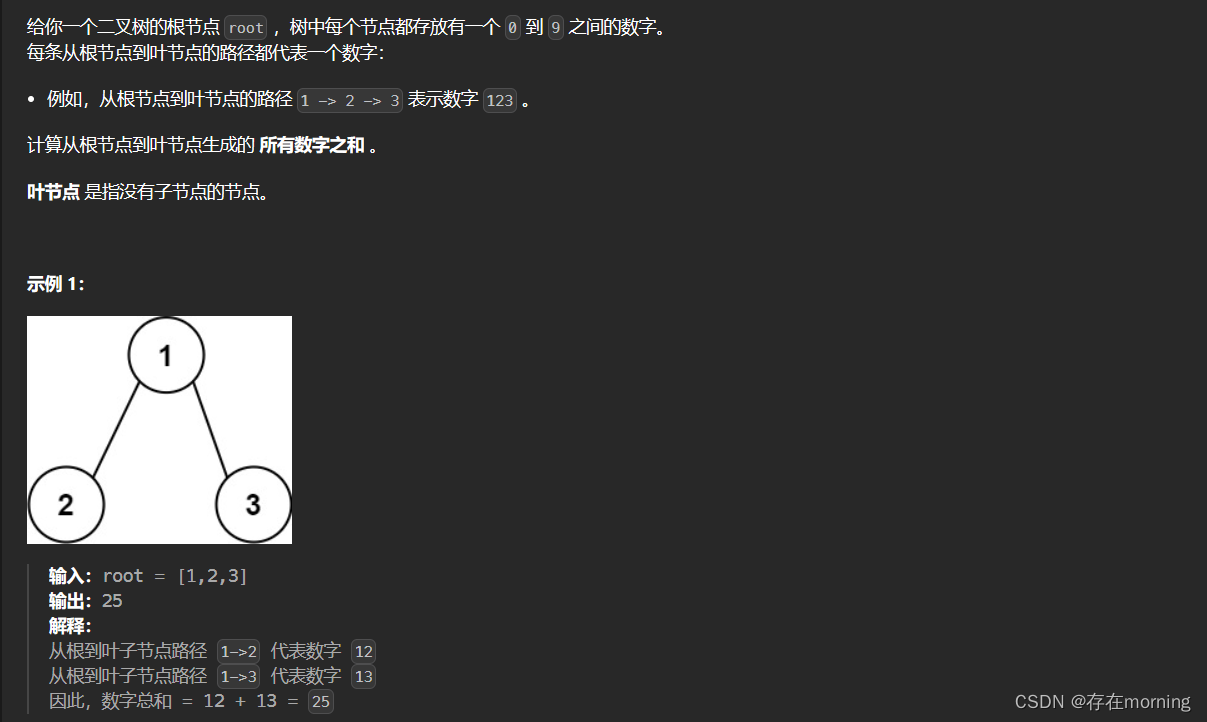
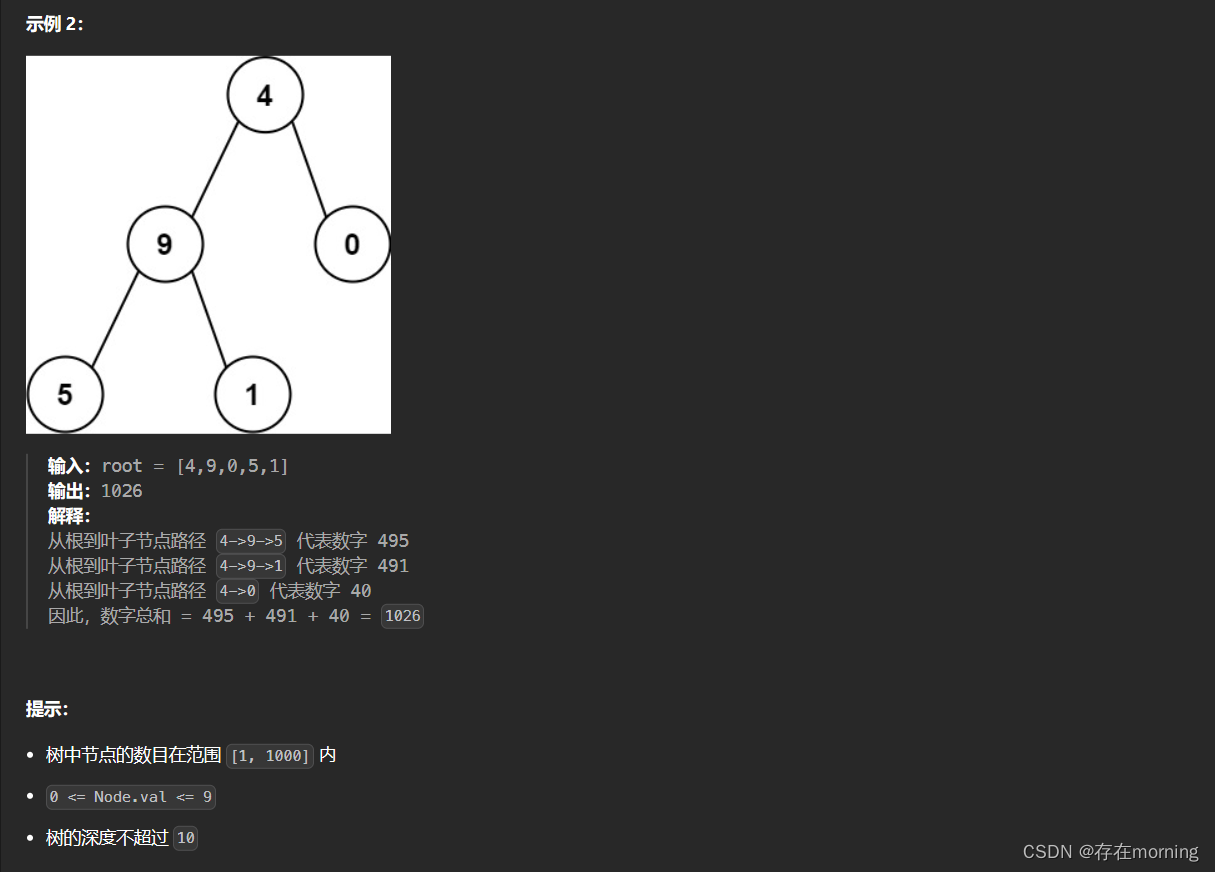
解题思路
原题解地址,这道题中,二叉树的每条从根节点到叶子节点的路径都代表一个数字。其实,每个节点都对应一个数字,等于其父节点对应的数字乘以 10 再加上该节点的值(这里假设根节点的父节点对应的数字是 0)。只要计算出每个叶子节点对应的数字,然后计算所有叶子节点对应的数字之和,即可得到结果。可以通过深度优先搜索和广度优先搜索实现。
深度优先搜索DFS
深度优先搜索是很直观的做法。从根节点开始,遍历每个节点,如果遇到叶子节点,则将叶子节点对应的数字加到数字之和。如果当前节点不是叶子节点,则计算其子节点对应的数字,然后对子节点递归遍历
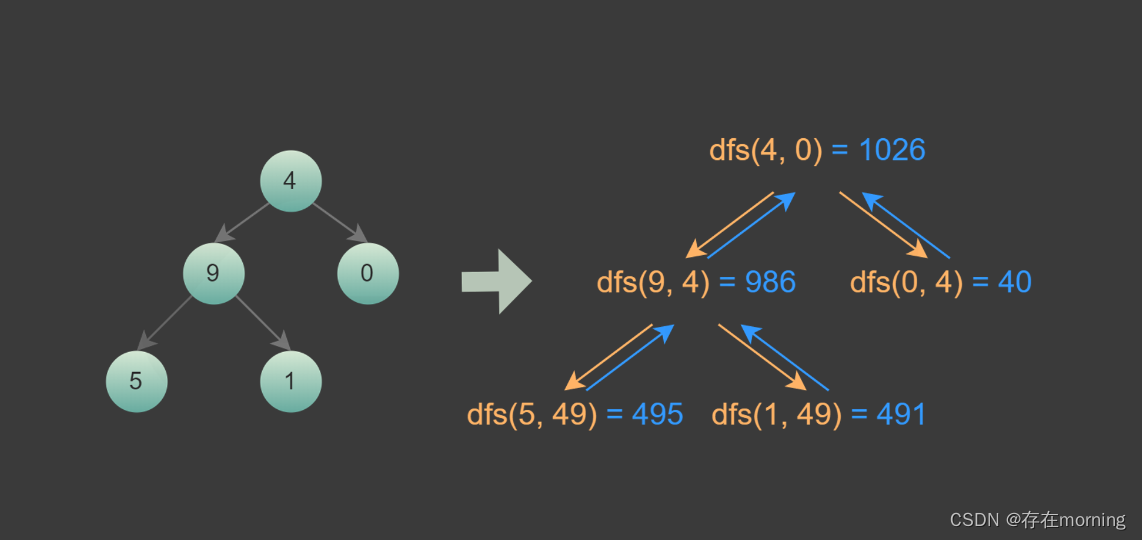
广度优先搜索BFS
使用广度优先搜索,需要维护两个队列,分别存储节点和节点对应的数字。
- 初始时,将根节点和根节点的值分别加入两个队列。每次从两个队列分别取出一个节点和一个数字,进行如下操作:
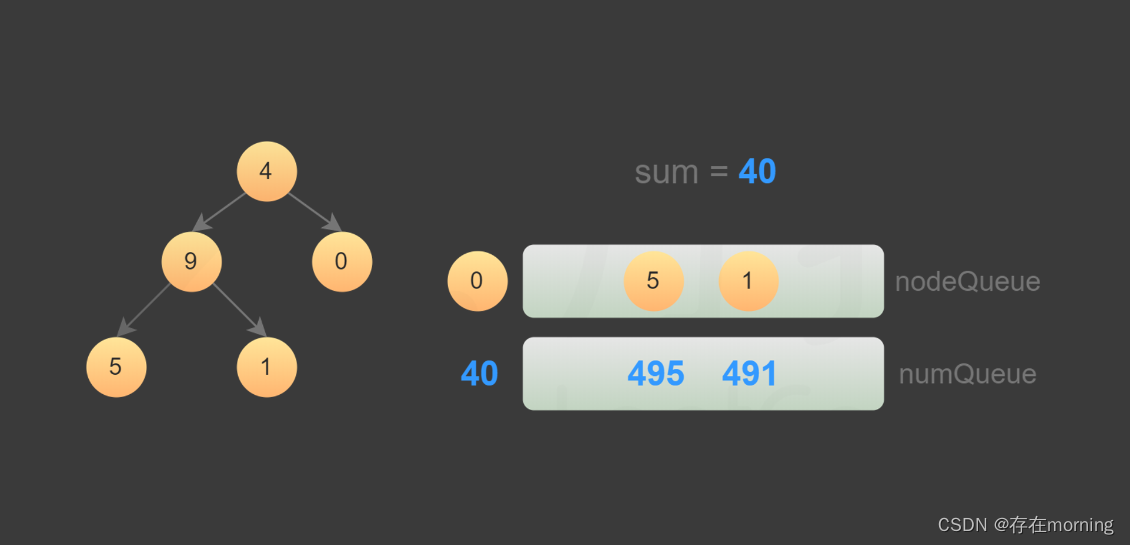
- 如果当前节点是叶子节点,则将该节点对应的数字加到数字之和;
- 如果当前节点不是叶子节点,则获得当前节点的非空子节点,并根据当前节点对应的数字和子节点的值计算子节点对应的数字,然后将子节点和子节点对应的数字分别加入两个队列。
搜索结束后,即可得到所有叶子节点对应的数字之和。
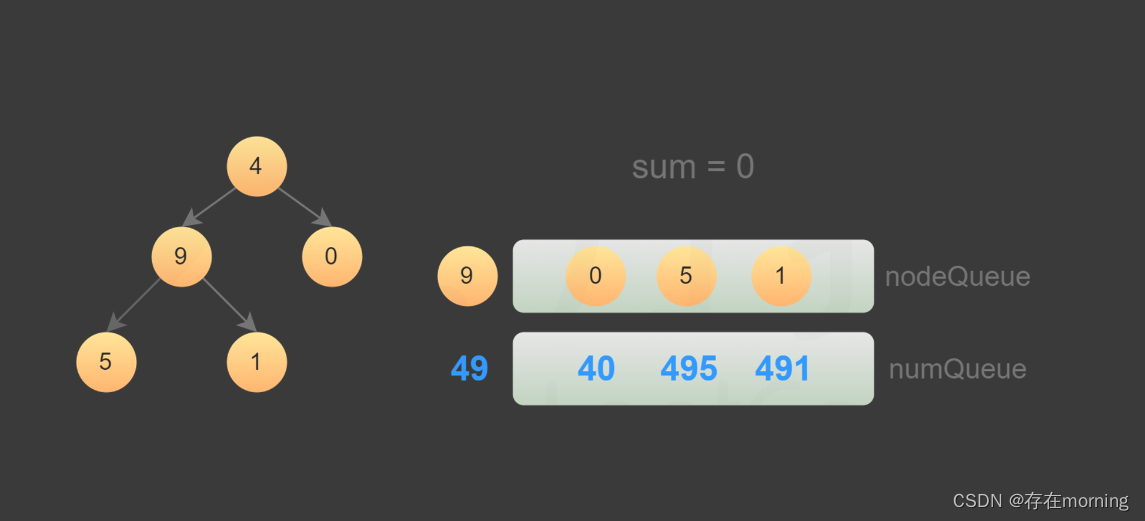
按照数值队列顺序加上了节点对应的值
代码实现
分别用DFS和BFS实现
DFS代码实现
给出代码实现基本档案
基本数据结构:二叉树
辅助数据结构:无
算法:递归
技巧:无
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
当然包括但不限于以上
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int sumNumbers(TreeNode root) {return dfsSum(root, 0);}private int dfsSum(TreeNode node, int preIndex) {// 1 递归终止,越过叶子节点,返回0;if (node == null) {return 0;}// 2 计算到当前节点的数值int curValue = preIndex * 10 + node.val;// 3 判断当前节点是否为叶子节点,到叶子节点则返回叶子节点值,非叶子节点的和为左右子节点的和if (node.left == null && node.right == null) {return curValue;} else {return dfsSum(node.left, curValue) + dfsSum(node.right, curValue);}}
}
BFS代码实现
给出代码实现基本档案
基本数据结构:二叉树
辅助数据结构:队列
算法:迭代
技巧:无
其中数据结构、算法和技巧分别来自:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
- 技巧:双指针、滑动窗口、中心扩散
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public int sumNumbers(TreeNode root) {// 1 入参判断,如果root为空,返回0if (root == null) {return 0;}// 2 定义两个队列,一个为节点队列,一个为 节点值队列(用于存放当前节点为止的数字)Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();Queue<Integer> numQueue = new LinkedList<Integer>();nodeQueue.offer(root);numQueue.offer(root.val);// 3 借助队列进行层次遍历int sum = 0;while (!nodeQueue.isEmpty()) {// 3-1 处理队头元素,获取节点和截止当前节点的数值TreeNode curNode = nodeQueue.poll();int curValue = numQueue.poll();if (curNode.left == null && curNode.right == null) {// 到了叶子节点则只剩下节点值,累加即可sum += curValue;} else {// 如果左子节点不为空,则将左子节点入队,并且更新左子节点的截止数值if (curNode.left != null) {nodeQueue.offer(curNode.left);numQueue.offer(curValue * 10 + curNode.left.val);}// 如果右子节点不为空,则将右子节点入队,并且更新右子节点的截止数值if (curNode.right != null) {nodeQueue.offer(curNode.right);numQueue.offer(curValue * 10 + curNode.right.val);}}}return sum ;}}
复杂度分析
- 时间复杂度:O(N)。遍历了一遍二叉树,时间复杂度为O(N)
- 空间复杂度:O(N)。DFS时 递归最差情况下时间复杂度为O(N),BFS时队列占用空间O(N)
相关文章:

【数据结构-二叉树 八】【遍历求和】:求根到叶子节点数字之和
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【遍历求和】,使用【二叉树】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为&am…...

PHP知识大全
PHP知识大全 1. 变量如何定义?如何检查变量是否定义?如何删除一个变量?怎样检测变量是否设置? $定义 isset()// 检测变量是否设置 defined()// 检测常量是否设置unset()//销毁指定的变量 empty()// 检测…...

Jmeter常用参数化技巧总结!
说起接口测试,相信大家在工作中用的最多的还是Jmeter。 JMeter是一个100%的纯Java桌面应用,由Apache组织的开放源代码项目,它是功能和性能测试的工具。具有高可扩展性、支持Web(HTTP/HTTPS)、SOAP、FTP、JAVA 等多种协议。 在做…...
iTunes更新iOS17出现发生未知错误4000的原因和解决方案
有不少人使用iTunes更新iOS 17时出现「无法更新iPhone发生未知的错误4000」的错误提示,不仅不知道iTunes升级失败的原因,也无从解决iPhone无法更新4000的问题。 小编今天就分享iPhone更新iOS系统出现4000错误提示的原因和对应的解决方案。 为什么iPhone…...
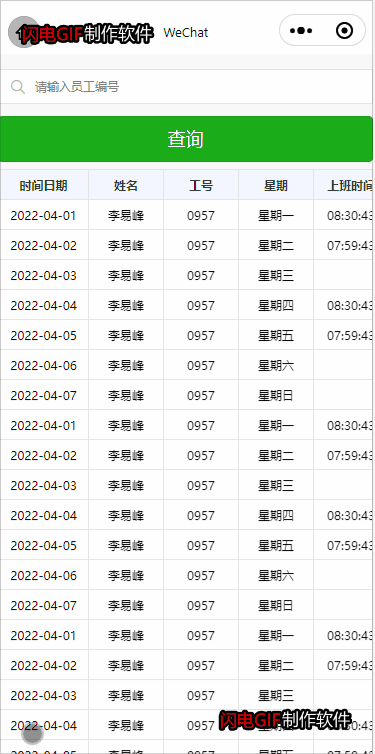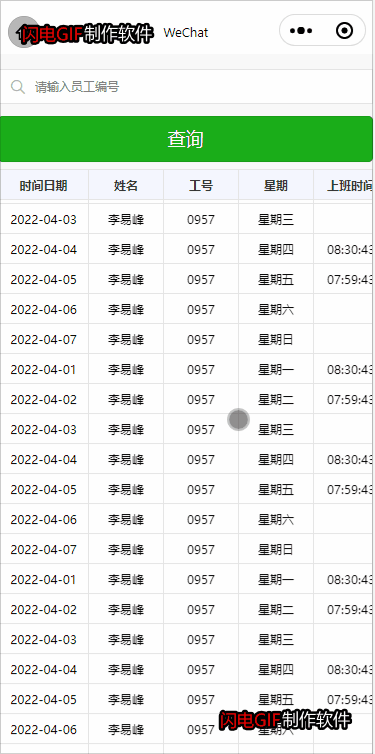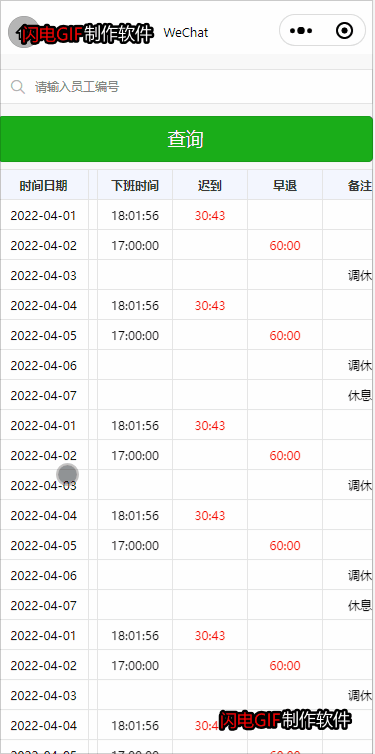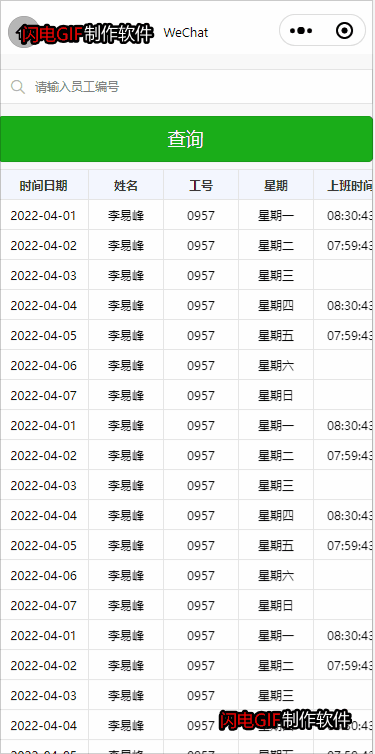
微信小程序 table表格 固定表头和首列 右侧表格可以左右滚动
(一) 1.左侧一列固定不动 2.右侧表格内容可以左右滚动 3.单元格内容平均分配 4.每一行行高可以由内容撑开 通过 js 设置左侧一列行高与右侧表格内容行高保持一致 1.1 效果图 1.2 tabble.wxml <view classtable><!-- 左侧固定 --><view classtable_left_colum…...

Final Cut Pro 10.6.10中文用法儿
Final Cut Pro是一款专业视频编辑软件,主要用于影片的后期剪辑、调色、特效、音频处理等方面。 Final Cut Pro for Mac(fcpx视频剪辑) 10.6.10中文版 以下是一些基本的使用方法和快捷键: 添加素材: 在检视器中,可以使用E快捷键把所选素材片…...

【网络安全---XSS漏洞(1)】XSS漏洞原理,产生原因,以及XSS漏洞的分类。附带案例和payload让你快速学习XSS漏洞
以pikachu靶场为例子进行讲解,pikachu靶场的搭建请参考以下博客; 【网路安全 --- pikachu靶场安装】超详细的pikachu靶场安装教程(提供靶场代码及工具)_网络安全_Aini的博客-CSDN博客【网路安全 --- pikachu靶场安装】超详细的pi…...

云计算:常用系统前端与后端框架
目录 一、理论 1.前端 2.后端 一、理论 1.前端 (1)JavaScript框架 JQuery.JS ZeptoJS(与jquery类似) SUI.Mobile Node.JS (服务端) angular.Js (模型,scope作用域,controller, 依赖注入,MVVM) :前端MVC . requir…...
asp.net闲置物品购物网系统VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio
一、源码特点 asp.net闲置物品购物网系统是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为sqlserver2008,使用c#语 言开发 asp.net 闲置物品购物网 二、功…...

一般纳税人缺少进项票,如何降低税负压力?
《梅梅谈税》专注于企业税务筹划!助力企业合理、合规、合法进行节税税收筹划! 大部分一般纳税人企业通常都存在进项和成本发票欠缺的问题,而进项发票欠缺,就会导致企业的增值税和企业所得税税负压力过大,那么如何解决…...

UniAD 论文学习
一、解决了什么问题? 当前的自动驾驶方案大致由感知(检测、跟踪、建图)、预测(motion、occupancy)和规划三个模块构成。 为了实现各种功能,智驾方案大致包括两种路线。一种是针对每个任务都部署一个模型&a…...
用冒泡排序模拟实现qsort()函数交换整数)
(c语言)用冒泡排序模拟实现qsort()函数交换整数
#include<stdio.h> int cmp(const void* x1, const void* x2) { return (*(int*)x1 - *(int*)x2); } void Swap(char* x, char* y, int width) //将两个数改为char*类型,每次只交换一个字节,直到将int*的四个字节全部交换一遍 { int i 0; f…...

【Java-LangChain:使用 ChatGPT API 搭建系统-11】用 ChatGPT API 构建系统 总结篇
第十一章,用 ChatGPT API 构建系统 总结篇 本课程详细介绍了 LLM 工作原理,包括分词器(tokenizer)的细节、评估用户输入的质量和安全性的方法、使用思维链作为 Prompt、通过链式 Prompt 分割任务以及返回用户前检查输出等。 本课…...

3D 生成重建004-DreamFusion and SJC :TEXT-TO-3D USING 2D DIFFUSION
3D 生成重建004-DreamFusion and SJC :TEXT-TO-3D USING 2D DIFFUSION 文章目录 0 论文工作1 论文方法1.1论文方法1.2 CFG1.3影响1.4 SJC 2 效果 0 论文工作 对于生成任务,我们是需要有一个数据样本,让模型去学习数据分布 p ( x ) p(x) p(x…...

机械臂抓取的产业落地进展与思考
工业机械臂是一种能够模拟人类手臂动作的机械装置,具有高精度、高速度和高灵活性的特点。近年来,随着人工智能和机器人技术的快速发展,机械臂在工业生产、物流仓储、医疗护理等领域得到了广泛应用。机械臂抓取技术作为机械臂的核心功能之一&a…...
分析)
【RuoYi-Cloud项目研究】【ruoyi-auth模块】登录请求(/login)分析
文章目录 0. 网关如何处理登录请求1. Controller1.1. 获取用户信息1.2. 创建用户的token 2. Service2.1. FeignClient远程查询用户信息2.2. 验证密码 3. 何时刷新 token,如何刷新【本文重点】 本文主要是分析登录请求 /login 的过程。 调用过程是:ruoyi-…...
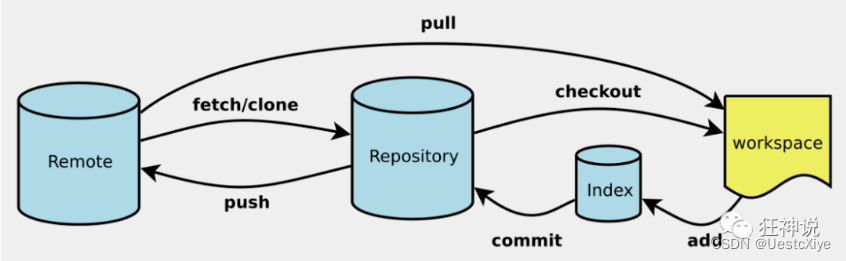
Git 学习笔记 | Git 项目创建及克隆
Git 学习笔记 | Git 项目创建及克隆 Git 学习笔记 | Git 项目创建及克隆创建工作目录与常用指令本地仓库搭建克隆远程仓库 Git 学习笔记 | Git 项目创建及克隆 创建工作目录与常用指令 工作目录(WorkSpace)一般就是你希望Git帮助你管理的文件夹,可以是…...

C++默认参数(实参)
在本文中,您将学习什么是默认参数,如何使用它们以及使用它的必要声明。在C 编程中,您可以提供函数参数的默认值。默认参数背后的想法很简单。如果通过传递参数调用函数,则这些参数将由函数使用。但是,如果在调用函数时…...

Datax数据同步支持SqlServer 主键自增
允许写入的SQL SET IDENTITY_INSERT table_name ON;-- 插入数据,指定主键值 INSERT INTO table_name (id, column1, column2, ...) VALUES (new_id_value, value1, value2, ...);SET IDENTITY_INSERT table_name OFF; 写入插件处理 核心类:com.alibab…...

C++开发学习笔记3
C 中枚举的使用 在C中,枚举常量(Enumeration Constants)是一种定义命名常量的方式。枚举类型允许我们为一组相关的常量赋予有意义的名称,并将它们作为一个独立的类型来使用。 以下是定义和使用枚举常量的示例: enum…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
