数据结构-图-最短路径问题
最短路径问题
- 单源最短路径
- Dijkstra
- 算法原理
- 代码实现
- Bellman-Ford
- 算法原理
- 代码实现
- SPFA优化
- SPFA代码实现
- 多元最短路径
- Floyd-Warshall
- 算法原理
- 代码实现
单源最短路径
🚀最短路径:从图G的某个顶点出发到达另一个顶点的最短路径,其中最短是指路径上边的权值和最小。
🚀单源最短路径:从图G中的某一顶点出发到达其余顶点的最短路径。
Dijkstra
算法原理
🚀针对一个带权有向图,将所有的顶点划分为两个集合S和Q,S是已经确定最短路径的顶点结合,Q是还未确定最短路径的顶点集合。每次从Q中找出一个从起点s到达该结点代价最小(权值和最小)的结点u(可见迪杰斯特拉算法同样采取的是贪心策略),将u从集合Q中移除,并放入S中,对u所邻接的顶点做一次松弛操作。松弛操作即对结点u的邻接点v,判断从起点s到u的代价+u到v的代价是否小于s到v的代价,若小于那么对s到v的代价替换为s到u的代价+u到v的代价。这样依次从Q中选出结点u,直到Q为空为止。
算法特点:比较与其他最短路径的算法,迪杰斯特拉算法的效率较优。但是,此算法只能用于没有负权值的图。
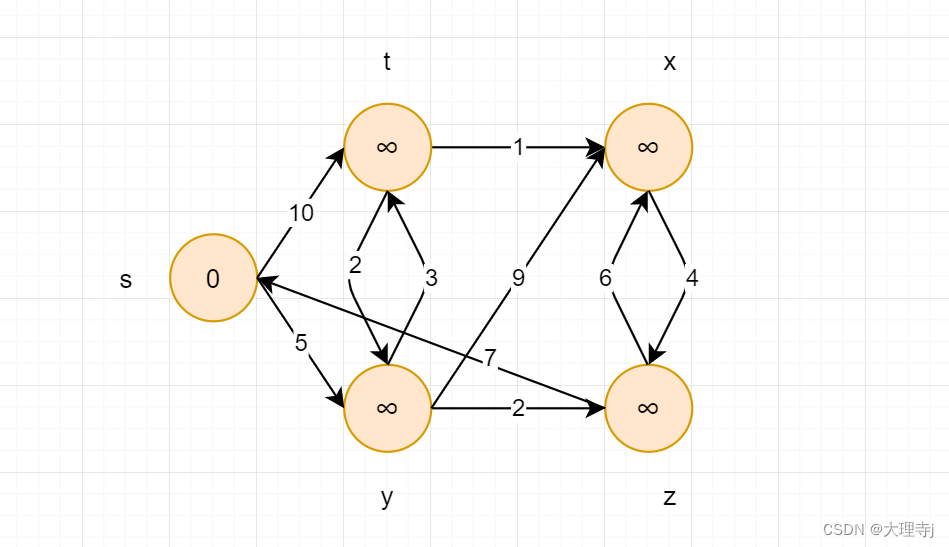
源点为s,即求s到达其他顶点的最短路径。在初始时,s到达其他边的路径长度均为无穷大 ,到达自身的距离为0。
算法执行过程:
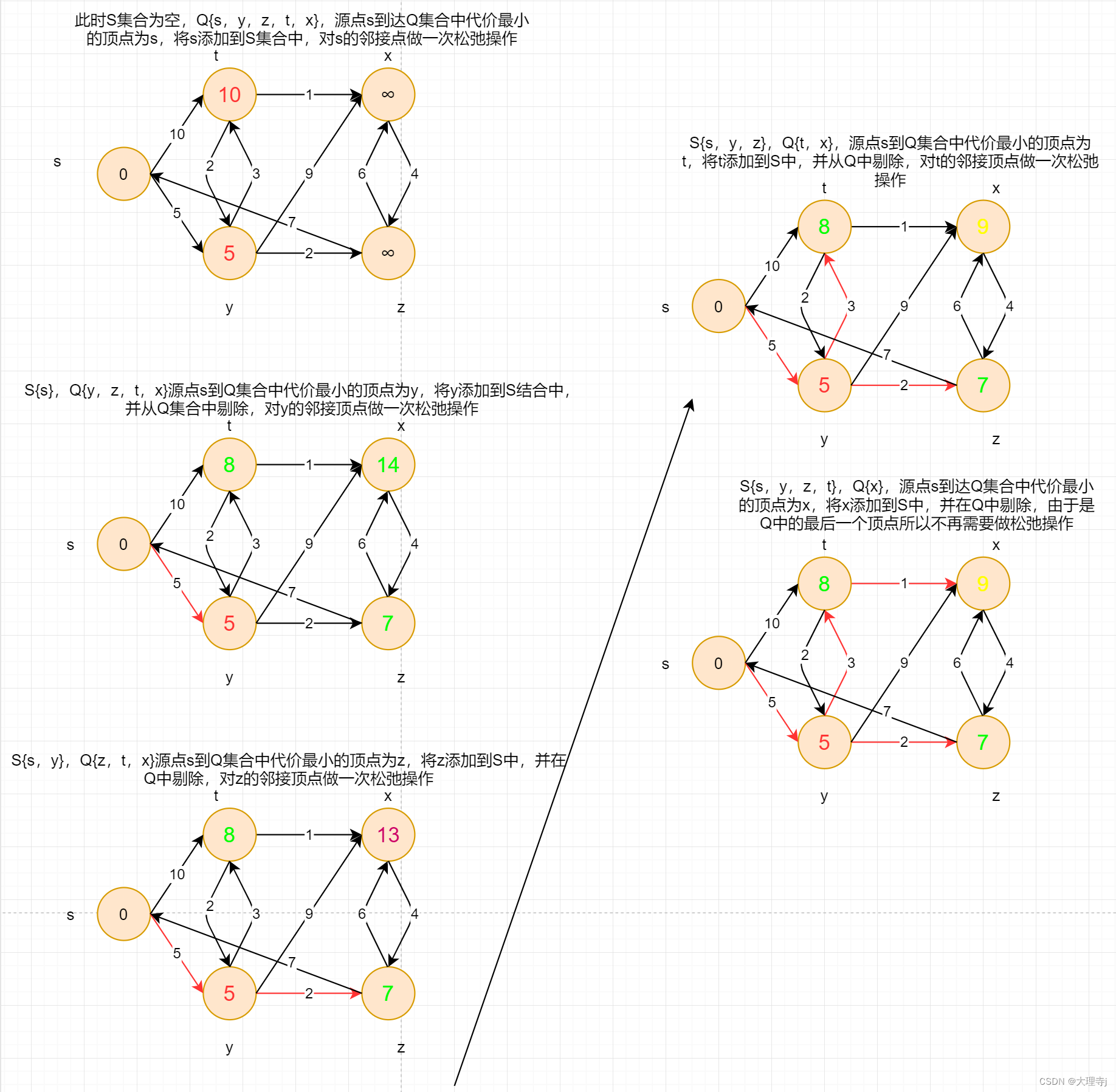
代码实现
void Dijkstra(const V& src, std::vector<W>& dist, std::vector<int>& parent_path) {//初始化工作size_t n = _vertex.size();size_t srci = this->GetVertexIndex(src);dist.resize(n, W_MAX);dist[srci] = 0;parent_path.resize(n, -1);std::vector<bool> S(n, false); //已选出的顶点集合Sfor (size_t i = 0; i < n; i++) {//从dist中选出最短的一条边,S->usize_t u = -1;W min_eg = W_MAX;for (size_t j = 0; j < n; j++) {if (dist[j] < min_eg && false == S[j]) {u = j;min_eg = dist[j];}}//将这个顶点添加到S集合中S[u] = true;//更新从起始点srci能够到达的其他点的最短路径dist数组for (size_t i = 0; i < n; i++) {if (_matrix[u][i] != W_MAX && false == S[i] && dist[u] + _matrix[u][i] < dist[i]) {dist[i] = dist[u] + _matrix[u][i];parent_path[i] = u;}}}
}
dist数组和parent_path数组解释:将源点s到达其他顶点的最短路径数值存储在dist数组中,dist[i]即为源点s到达i号顶点的最短距离。parent_path数组用来记录源点s到达其他顶点的最短路径,采用的是双亲表示法,即该结点存储的内容为源点s到达这个结点路径上的上一个结点的下标。
🚀上面例子中最终两个数值的内容如下:

Bellman-Ford
算法原理
🚀迪杰斯特拉算法不能解决带负权值路径的情况,贝尔曼算法可以解决这一问题。相比于迪杰斯特拉的贪心策略,贝尔曼算法是一种较为暴力的解法,即对每一个结点都做一次松弛操作,但是一轮松弛操作往往不能得到最终结果,存在最短路径于最短路径权值和对应不上的情况,所以要经过多轮更新才能得到最终结果。最多轮次为n-1轮(n:顶点个数),如果说第n轮更新还能有顶点松弛成功说明存在权值和为负数的环路情况,这种情况贝尔曼算法也是解决不了的(权值和为负数的环路意味着每轮更新都能得到一个更小的结果,是无休止的)。
只经过一轮更新不能的到最终结果的例子:
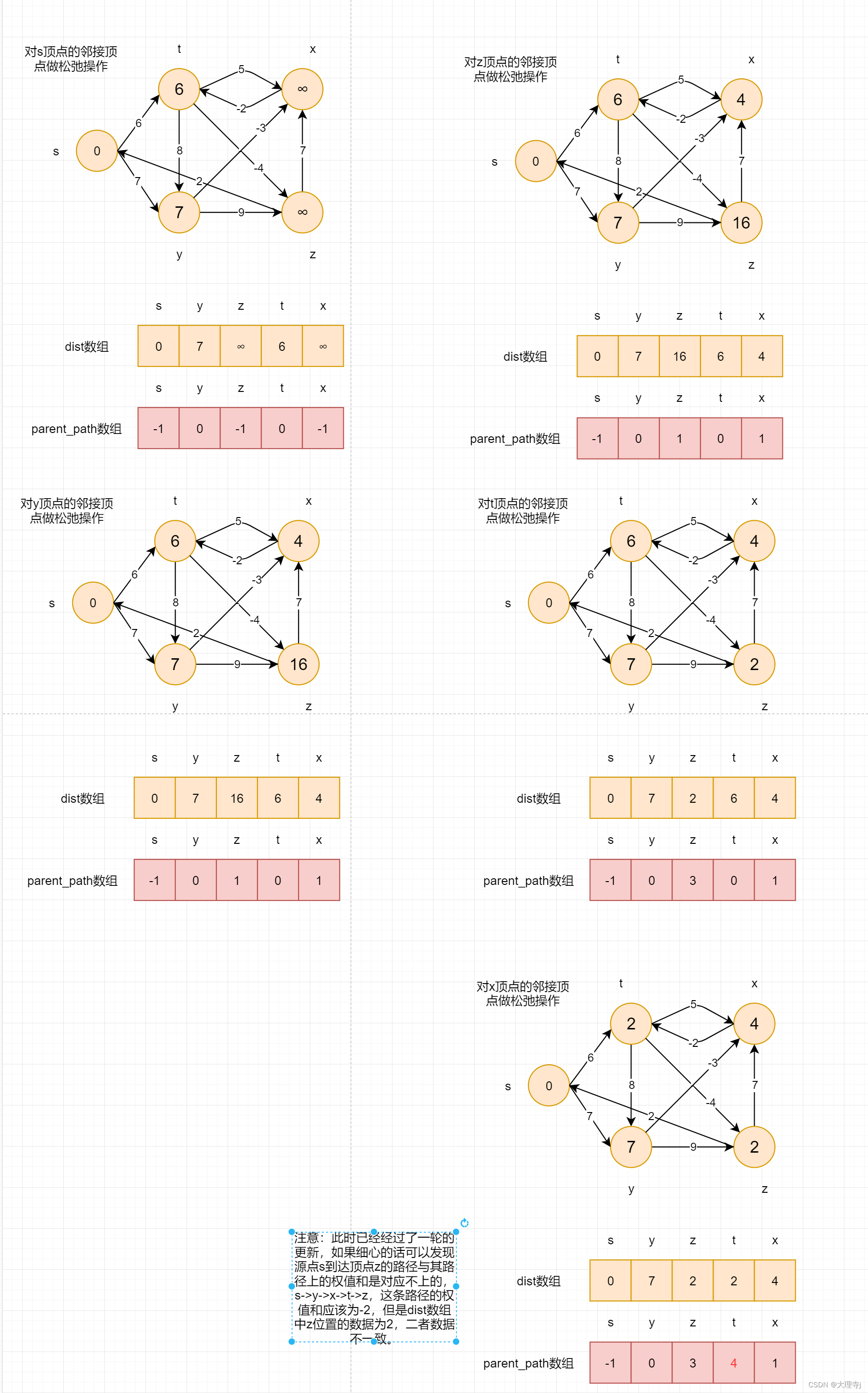
产生上图中这样结果的原因在于更新源点s到达z顶点的最短路径是由对t顶点的邻接顶点做松弛操作得到的,但是在更新源点s到达z的最短路径之后,在对x的邻接顶点做松弛操作的时候,又重新修改了源点s到达t顶点的最短路径,此时在parent_path数组中t位置的数据修改成了x的下标,同样也因此导致了s到达z顶点的路径于路径上的权值和不一致的情况。所以要对t的邻接顶点重新做一次松弛操作,上面这种情况再对t的邻接顶点做一次松弛操作就可以解决问题,但是对于其他更为复杂的问题可能仍旧需要新一轮的松弛操作。那么,松弛操作轮数的上限是多少次呢?n - 1次因为源点出发到达另一个顶点的最短路径至多经过n - 1条边,所以至多经过n - 1轮的更新就能得到最终结果,但是如果第n轮时仍旧存在到达某个点的最短路径发生了更新,那么就说明存在权值和为负数的环路问题。
代码实现
bool Bellman(const V& src, std::vector<W>& dist, std::vector<int>& parent_path) {//初始化结构size_t n = _vertex.size();size_t srci = this->GetVertexIndex(src);dist.resize(n, W_MAX);dist[srci] = 0;parent_path.resize(n, -1);//寻找最短路径for (size_t k = 0; k < n - 1; ++k) {bool update = false;//update小的优化--如果此轮更新中没有任何一条边松弛成功,此时就可以break退出std::cout << "第" << k + 1 << "轮更新: \n";for (size_t i = 0; i < n; i++) {for (size_t j = 0; j < n; j++) {if (_matrix[i][j] != W_MAX && dist[i] + _matrix[i][j] < dist[j]) {update = true;dist[j] = dist[i] + _matrix[i][j];std::cout << i << "->" << j << ":" << dist[j] << std::endl;parent_path[j] = i;}}}if (false == update) {break;}}//如果经过n-1轮还能进行更新说明出现了负权值环路问题for (size_t i = 0; i < n; i++) {for (size_t j = 0; j < n; j++) {if (_matrix[i][j] != W_MAX && dist[i] + _matrix[i][j] < dist[j]) {return false;}}}return true;
}
SPFA优化
🚀在上面分析一轮的松弛操作可能不能得到最终结果的问题时,解决方案就是再对t顶点的邻接顶点做一次松弛操作即可,并不用再对其他顶点做一次松弛操作,也就是说如果要在下一轮中再次对某个顶点的邻接顶点做松弛操作,那么这个顶点一定在本轮中得到了最短路径的更新,否则其不会对其他顶点产生影响。
🚀SPFA算法就是对上面代码中写的贝尔曼算法的一个优化,就是说如果要在下一轮中再次对某个顶点的邻接顶点做松弛操作,那么这个顶点一定在本轮中得到了最短路径的更新,所以在第一轮更新中所有顶点都需要更新,把所有的顶点都入队列,在后续的更新中,如果某个顶点在本轮没有被更新那么其也不会对其他顶点产生影响,就不用再次入队列,相反需要再次入队列, 这样循环置队列为空即可。
SPFA代码实现
void BellmanSPFA(const V& src, std::vector<W>& dist, std::vector<int>& parent_path) {//初始化结构size_t n = _vertex.size();size_t srci = this->GetVertexIndex(src);dist.resize(n, W_MAX);dist[srci] = 0;parent_path.resize(n, -1);std::queue<size_t> q;std::vector<bool> flag(n, false);q.push(srci);flag[srci] = true;while (!q.empty()) {size_t top = q.front();q.pop();flag[top] = false;for (size_t i = 0; i < n; i++) {if (_matrix[top][i] != W_MAX && dist[top] + _matrix[top][i] < dist[i]) {dist[i] = dist[top] + _matrix[top][i];parent_path[i] = top;if (flag[i] == false) {q.push(i);flag[i] = true;}}}}
}
多元最短路径
Floyd-Warshall
算法原理
🚀佛洛依德算法是一个解决多源的最短路径问题的经典算法,它能够计算出每个顶点到达其余顶点的最短路径,对应用场景通常是带负权值的多源最短路径问题。
🚀佛洛依德算法采用的是动态规划的思想,顶点i到达顶点j的最短路径上至少经过了0个其他顶点,至多经过了n - 2个其他顶点,其状态标识可以定义为dp[i][j][m],标识顶点i到达顶点j的最短路径上经过了k个其余顶点,其余顶点就是除了起始顶点和终止顶点的其他顶点记作k(k有n-2种取值可能),所以如果i到j的最短路径经过k,那么dp[i][j][m] = dp[i][k][m-1] + dp[k][j][m-1],如果i到j的最短路径不经过k,dp[i][j][m] = dp[i][j][m-1],所以最终dp[i][j][m] = min(dp[i][j][m-1],dp[i][k][m-1]+dp[k][j][m-1])。在正常写代码时通常将其优化为二维的动态规划,因为第三维的m总是依赖于m-1的。
代码实现
void Floyd(std::vector<std::vector<W>>& dist, std::vector<std::vector<int>>& parent_path) {//初始化结构size_t n = _vertex.size();dist.resize(n);parent_path.resize(n);for (size_t i = 0; i < n; ++i) {dist[i].resize(n, W_MAX);parent_path[i].resize(n, -1);}//初始化直接相连的边for (size_t i = 0; i < n; i++) {for (size_t j = 0; j < n; j++) {if (_matrix[i][j] != W_MAX) {dist[i][j] = _matrix[i][j];parent_path[i][j] = i;}if (i == j) {dist[i][j] = 0;}}}//动态规划for (size_t k = 0; k < n; ++k) {for (size_t i = 0; i < n; ++i) {for (size_t j = 0; j < n; ++j) {if (dist[i][k] != W_MAX && dist[k][j] != W_MAX &&dist[i][k] + dist[k][j] < dist[i][j]) {//更新dist[i][j] = dist[i][k] + dist[k][j];parent_path[i][j] = parent_path[k][j];}}}}
}
相关文章:

数据结构-图-最短路径问题
最短路径问题 单源最短路径Dijkstra算法原理代码实现 Bellman-Ford算法原理代码实现SPFA优化SPFA代码实现 多元最短路径Floyd-Warshall算法原理代码实现 单源最短路径 🚀最短路径:从图G的某个顶点出发到达另一个顶点的最短路径,其中最短是指…...
-集群)
弹性资源组件elastic-resource设计(二)-集群
简介 弹性资源组件提供动态资源能力,是分布式系统关键基础设施,分布式datax,分布式索引,事件引擎都需要集群和资源的弹性资源能力,提高伸缩性和作业处理能力。 本文介绍弹性资源组件的设计,包括架构设计和详细设计,指导开发人员代码开发,设计基于《flink原理源码分析(一…...
Flink学习笔记(一):Flink重要概念和原理
文章目录 1、Flink 介绍2、Flink 概述3、Flink 组件介绍3.1、Deploy 物理部署层3.2、Runtime 核心层3.3、API&Libraries 层3.4、扩展库 4、Flink 四大基石4.1、Checkpoint4.2、State4.3、Time4.4、Window 5、Flink 的应用场景5.1、Event-driven Applications【事件驱动】5.…...

网络中的一些基本概念
数据共享本质是网络数据传输 ,即计算机之间通过网络来传输数据,也称为 网络通信 。 根据网络互连的规模不同,可以划分为局域网和广域网。 局域网 LAN 局域网,即 Local Area Network ,简称 LAN 。 Local 即标识了局…...

mysql中varchar长度为多少
一. varchar存储规则: 4.0版本以下,varchar(20),指的是20字节,如果存放UTF8汉字时,只能存6个(每个汉字3字节) 5.0版本以上,varchar(20),指的是20字符,无论存…...
python+selenium实现UI自动化(入门篇)
一、基础准备。 python环境安装,参考:CSDN pycharm安装,参考:CSDN 谷歌浏览器驱动配置,参考:CSDN二、新建pycharm项目 截图中,上面是项目地址(可以提前在指定位置创建文件夹…...

深度学习基础知识 nn.Sequential | nn.ModuleList | nn.ModuleDict
深度学习基础知识 nn.Sequential | nn.ModuleList | nn.ModuleDict 1、nn.Sequential 、 nn.ModuleList 、 nn.ModuleDict 类都继承自 Module 类。2、nn.Sequential、nn.ModuleList 和 nn.ModuleDict语法3、Sequential 、ModuleDict、 ModuleList 的区别…...

【DevOps】搭建你的第一个 Docker 应用栈
搭建你的第一个 Docker 应用栈 1.Docker 集群部署2.第一个 Hello World2.1 获取应用栈各节点所需镜像2.2 应用栈容器节点互联2.3 应用栈容器节点启动2.4 应用栈容器节点的配置2.4.1 Redis Master 主数据库容器节点的配置2.4.2 Redis Slave 从数据库容器节点的配置2.4.3 Redis 数…...
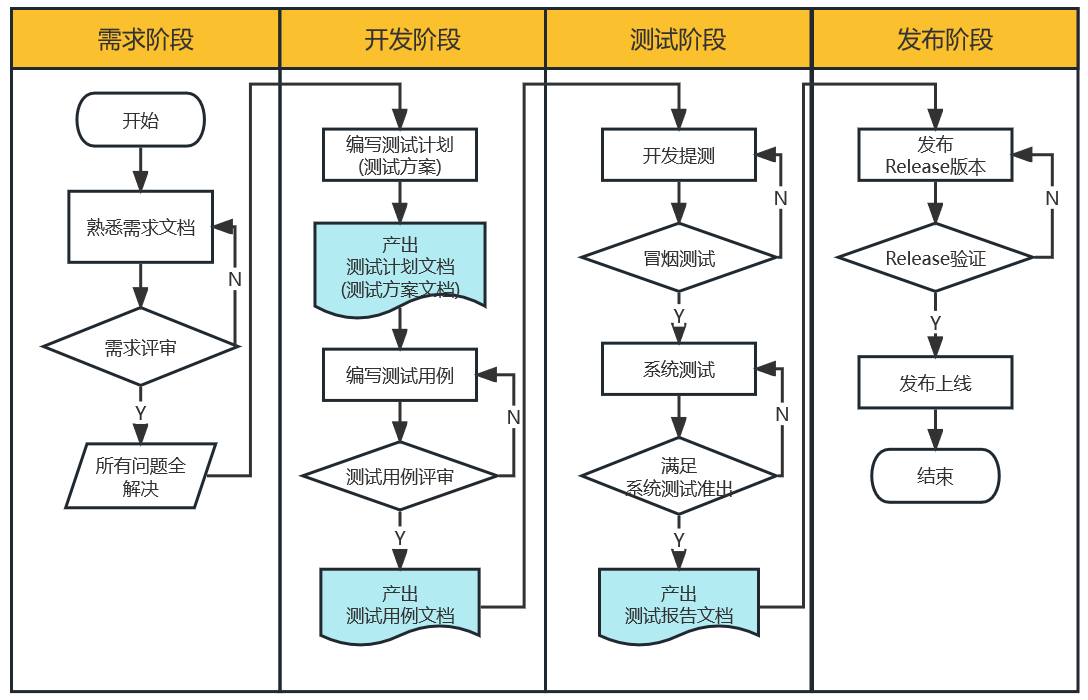
软件测试职业生涯需要编写的全套文档模板,收藏这一篇就够了 ~
作为一名测试工程师,在整个的职业生涯中,会涉及到各种不同类型的文档编写,大体包括如下: 对应文档模板及文档编写视频如下: 一、测试岗位必备的文档 在一个常规的软件测试流程中,会涉及到测试计划、测试方…...

【Kubernetes】Pod——k8s中最重要的对象之一
Pod是什么?如何使用Pod?资源共享和通信Pod 中的存储Pod 联网:跨 Pod 通信 静态 Pod感谢 💖 Pod是什么? Pod是k8s中创建和管理的、最小的可部署的计算单元。它包含一个或多个容器。就像豌豆荚里面包含了多个豌豆一样。…...

vue-cli-service: command not found问题解决
解决方案:重新安装一下: npm install -g vue/cli...

每日一练 | 华为认证真题练习Day117
1、缺省情况下,广播网络上OSPF协议Deadtime是? A. 20s B. 40s C. 10s D. 30s 2、当两台OSPF路由器形成TWO-WAY邻居关系时,LSDB已完成同步,但是SPF算法尚未运行。 A. 对 B. 错 3、以下哪种协议不属于文件传输协? …...
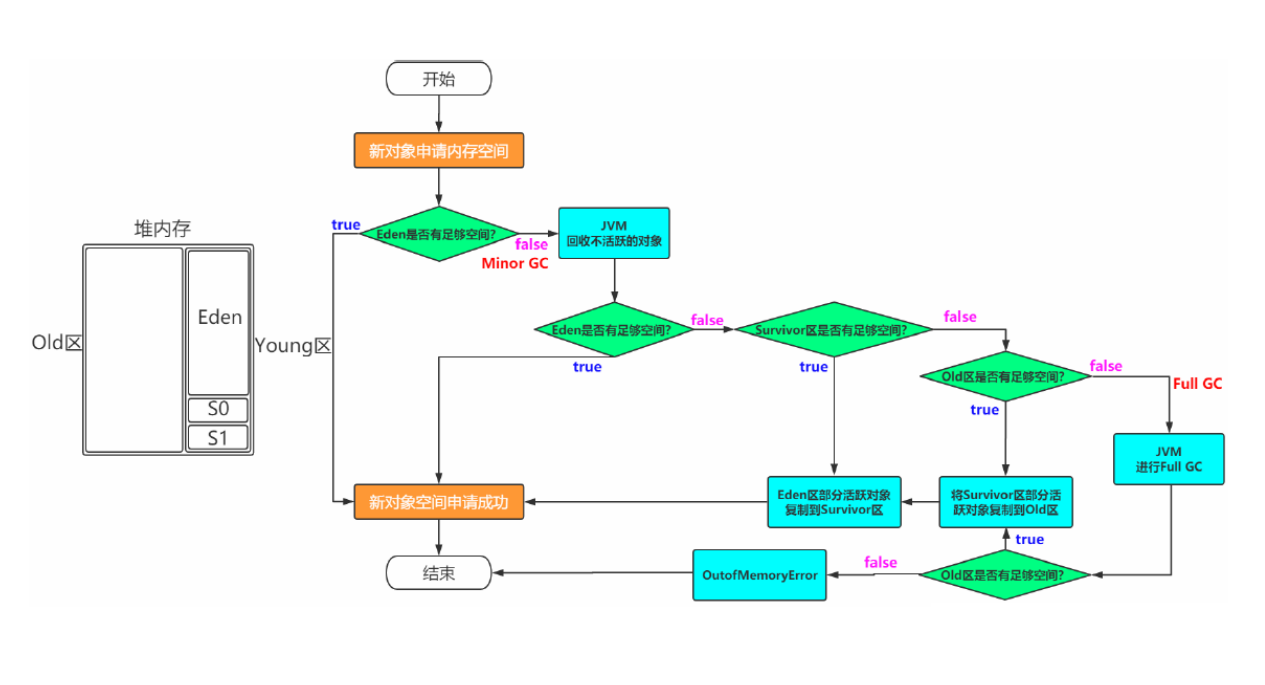
【JVM】垃圾回收(GC)详解
垃圾回收(GC)详解 一. 死亡对象的判断算法1. 引用计数算法2. 可达性分析算法 二. 垃圾回收算法1. 标记-清除算法2. 复制算法3. 标记-整理算法4. 分代算法 三. STW1. 为什么要 STW2. 什么情况下 STW 四. 垃圾收集器1. CMS收集器(老年代收集器&…...

阿里云服务器公网带宽多少钱1M?
阿里云服务器公网带宽计费模式按固定带宽”计费多少钱1M?地域不同带宽价格不同,北京、杭州、深圳等大陆地域价格是23元/Mbps每月,中国香港1M带宽价格是30元一个月,美国硅谷是30元一个月,日本东京1M带宽是25元一个月&am…...

应用DeepSORT实现目标跟踪
在ByteTrack被提出之前,可以说DeepSORT是最好的目标跟踪算法之一。本文,我们就来应用这个算法实现目标跟踪。 DeepSORT的官方网址是https://github.com/nwojke/deep_sort。但在这里,我们不使用官方的代码,而使用第三方代码&#…...

Beyond Compare 4 30天评估到期 解决方法
Beyond Compare 4 用习惯了,突然提示评估到期了,糟心😄 该方法将通过修改注册表,使BeyondCompare 版本4可以恢复到未评估状态,使其可以持续使用30天评估😄。 修改注册表 第一步:打开注册表。 在…...
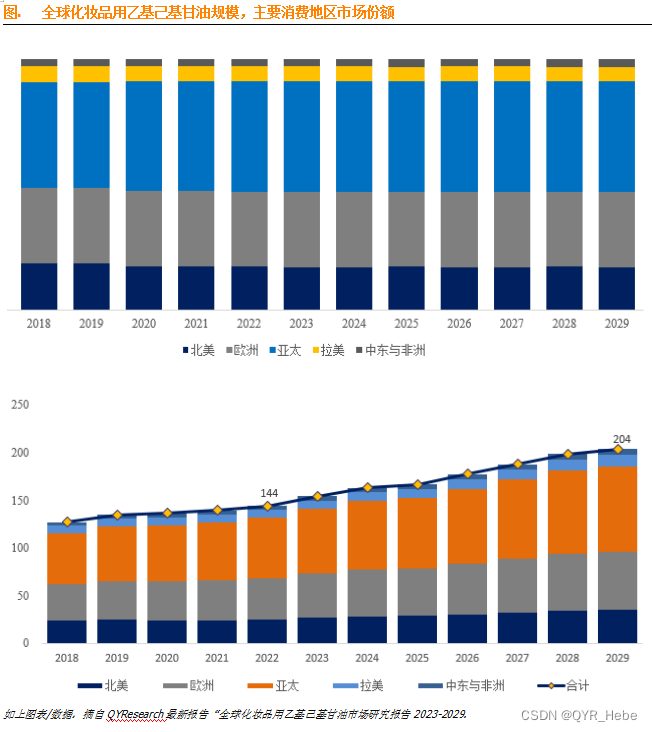
化妆品用乙基己基甘油全球市场总体规模2023-2029
乙基己基甘油又名辛氧基甘油,分子式 C11H24O3,分子量 204.306,沸点 325℃,密度 0.962,无色液体,涂抹性能适中的润肤剂、保湿剂及润湿剂。它能够在提高配方滋润效果的同时又具有柔滑的肤感。加入在某些膏霜体…...
springboot家政服务管理平台springboot29
大家好✌!我是CZ淡陌。一名专注以理论为基础实战为主的技术博主,将再这里为大家分享优质的实战项目,本人在Java毕业设计领域有多年的经验,陆续会更新更多优质的Java实战项目,希望你能有所收获,少走一些弯路…...

【网络安全】如何保护IP地址?
使用防火墙是保护IP地址的一个重要手段。防火墙可以监控和过滤网络流量,并阻止未经授权的访问。一家网络安全公司的研究显示,超过80%的企业已经部署了防火墙来保护他们的网络和IP地址。 除了防火墙,定期更新操作系统和应用程序也是保护IP地址…...
2023年失业了,想学一门技术可以学什么?
有一个朋友,大厂毕业了,原本月薪估计有5w吧,年终奖也不错,所以早早的就买了房生了娃,一直是人生赢家的姿态。 但是今年突然就被毕业了,比起房货还有个几百万没还来说,他最想不通的是自己的价值…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
