【算法训练-数组 三】【数组矩阵】螺旋矩阵、旋转图像、搜索二维矩阵
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是螺旋矩阵,使用【二维数组】这个基本的数据结构来实现
螺旋矩阵【EASY】
二维数组的结构特性入手
题干
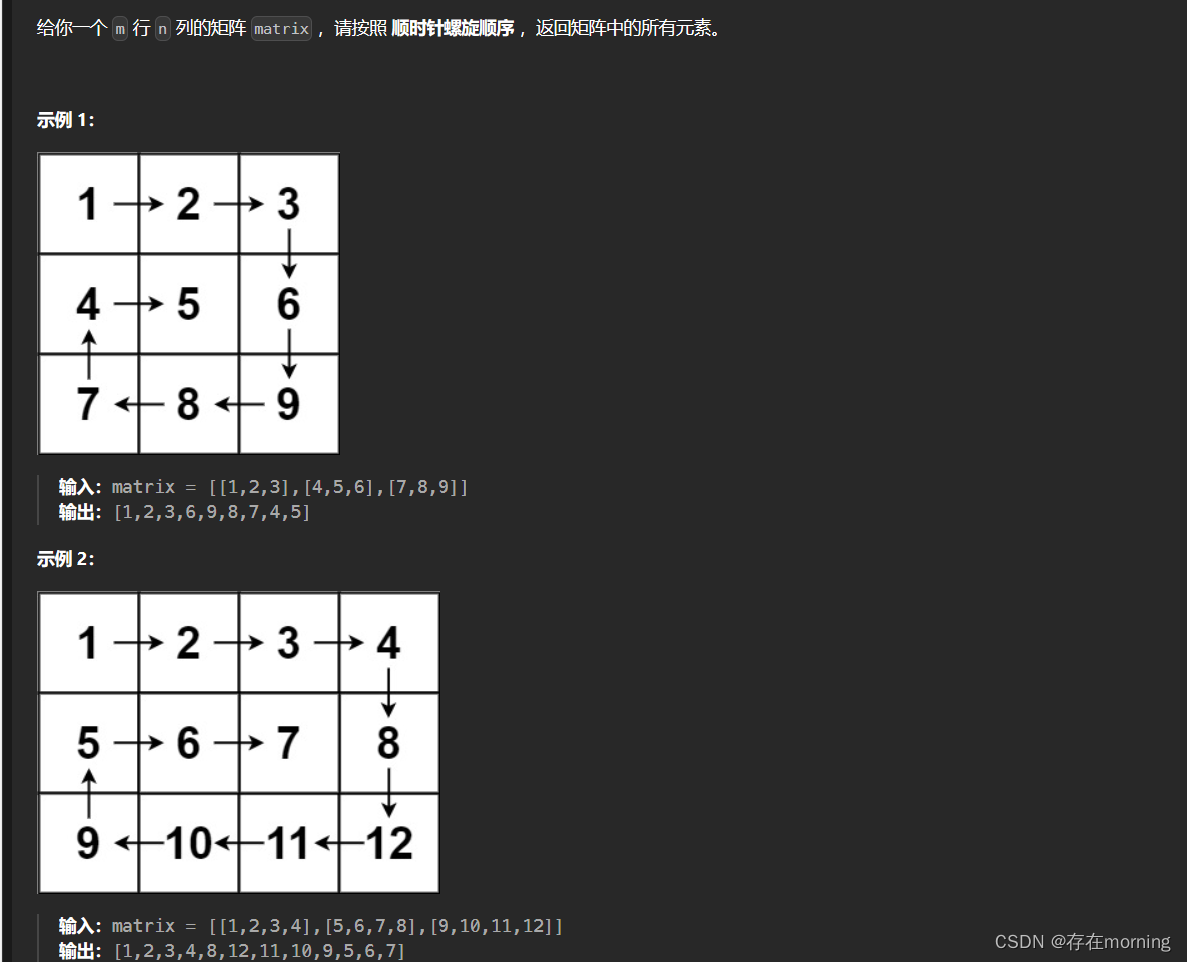
解题思路
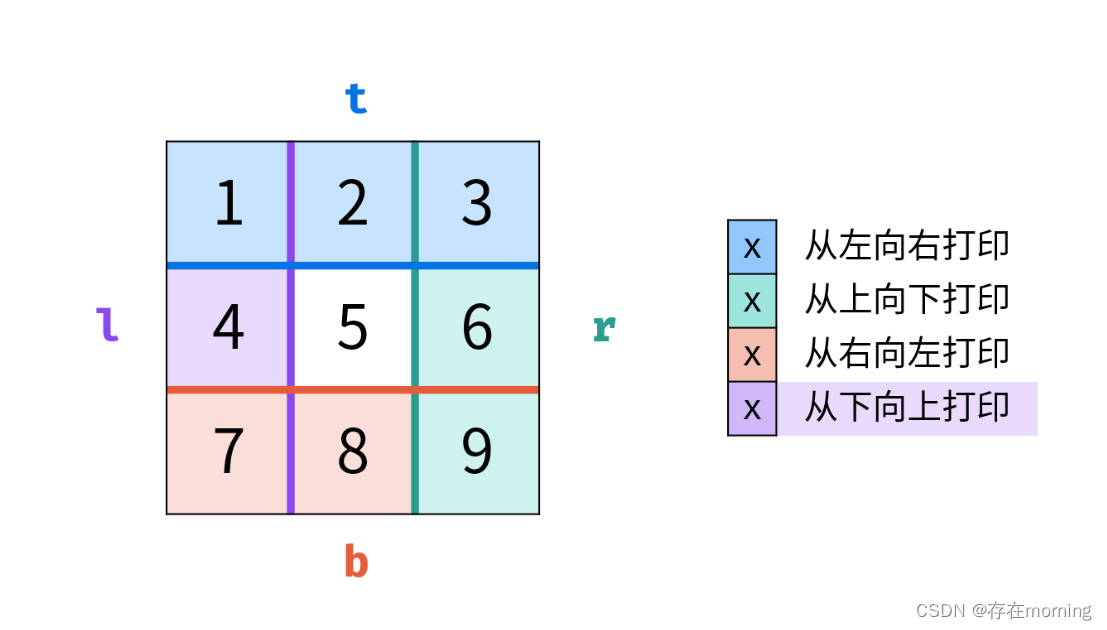
根据题目示例 matrix = [[1,2,3],[4,5,6],[7,8,9]] 的对应输出 [1,2,3,6,9,8,7,4,5] 可以发现,顺时针打印矩阵的顺序是 “从左向右、从上向下、从右向左、从下向上” 循环。
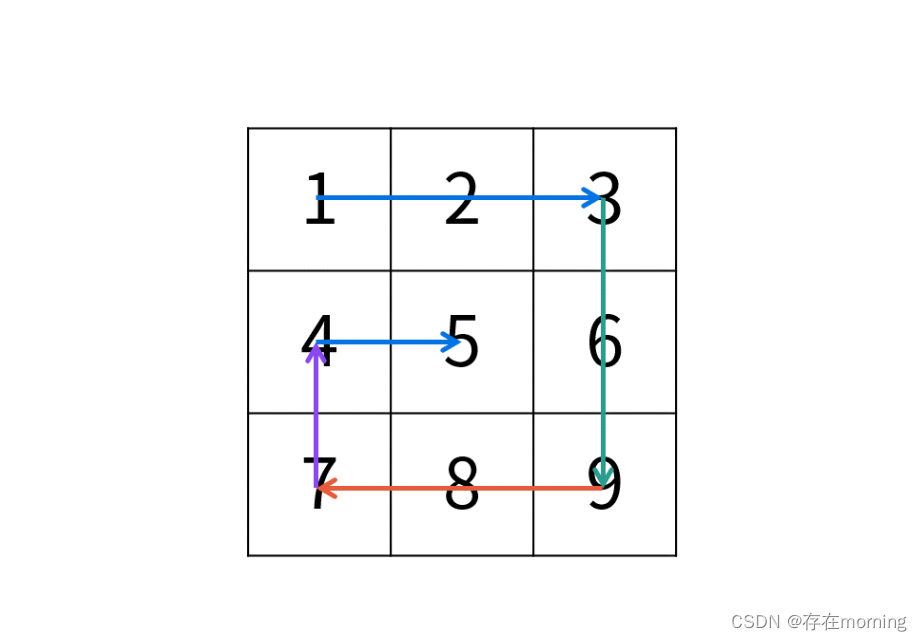
因此,考虑设定矩阵的 “左、上、右、下” 四个边界,模拟以上矩阵遍历顺序,算法流程:
- 空值处理: 当 matrix 为空时,直接返回空列表 [] 即可。
- 初始化: 矩阵 左、右、上、下 四个边界 l , r , t , b ,用于打印的结果列表 res 。
- 循环打印: “从左向右、从上向下、从右向左、从下向上” 四个方向循环打印。
- 根据边界打印,即将元素按顺序添加至列表 res 尾部。
- 边界向内收缩 1 (代表已被打印)。
- ** 判断边界是否相遇**(是否打印完毕),若打印完毕代表下一个方向无需打印,则跳出。
- 返回值: 返回 res 即可。
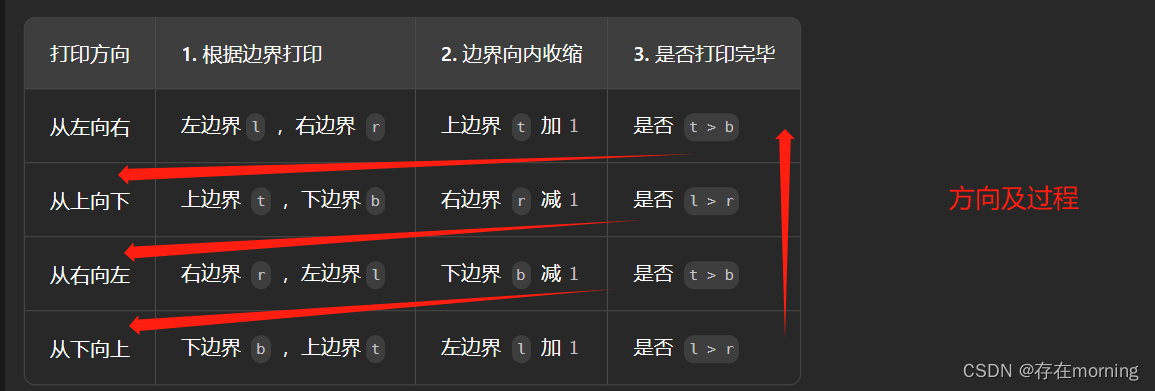
整体的打印过程
代码实现
基本数据结构:数组
辅助数据结构:无
算法:无
技巧:无
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param matrix int整型二维数组* @return int整型ArrayList*/public ArrayList<Integer> spiralOrder (int[][] matrix) {// 1 入参判断,如果为空数组,返回空集合if (matrix.length < 1) {return new ArrayList<Integer>();}// 2 定义四条边及返回值ArrayList<Integer> result = new ArrayList<Integer>();int left = 0;int right = matrix[0].length - 1;int top = 0;int bottom = matrix.length - 1;// 3 循环打印四条边while (true) {// 3-1 从左向右打印,明确左右边界,打印完后上边界向下移动,并判断是否有必要继续从上到下打印for (int i = left; i <= right; i++) {result.add(matrix[top][i]);}if (++top > bottom) {break;}// 3-2 从上向下打印,明确上下边界,打印完后右边界向左移动,并判断是否有必要继续从右到左打印for (int i = top; i <= bottom; i++) {result.add(matrix[i][right]);}if (left > --right) {break;}// 3-3 从右向左打印,明确左右边界,打印完后下边界向上移动,并判断是否有必要继续从下到上打印for (int i = right; i >= left; i--) {result.add(matrix[bottom][i]);}if (top > --bottom) {break;}// 3-4 从下向上打印,明确上下边界,打印完后左边界向右移动,并判断是否有必要继续从左到右打印for (int i = bottom; i >= top; i--) {result.add(matrix[i][left]);}if (++left > right) {break;}}return result;}
}
++top > bottom 等价于先给 top 自增 1 ,再判断++top > bottom 逻辑表达式
复杂度分析
- 时间复杂度 O(MN) : M,N分别为矩阵行数和列数。
- 空间复杂度 O(1) : 四个边界 l , r , t , b 使用常数大小的额外空间。
旋转图像
和螺旋矩阵类似,也是对一圈数值做处理
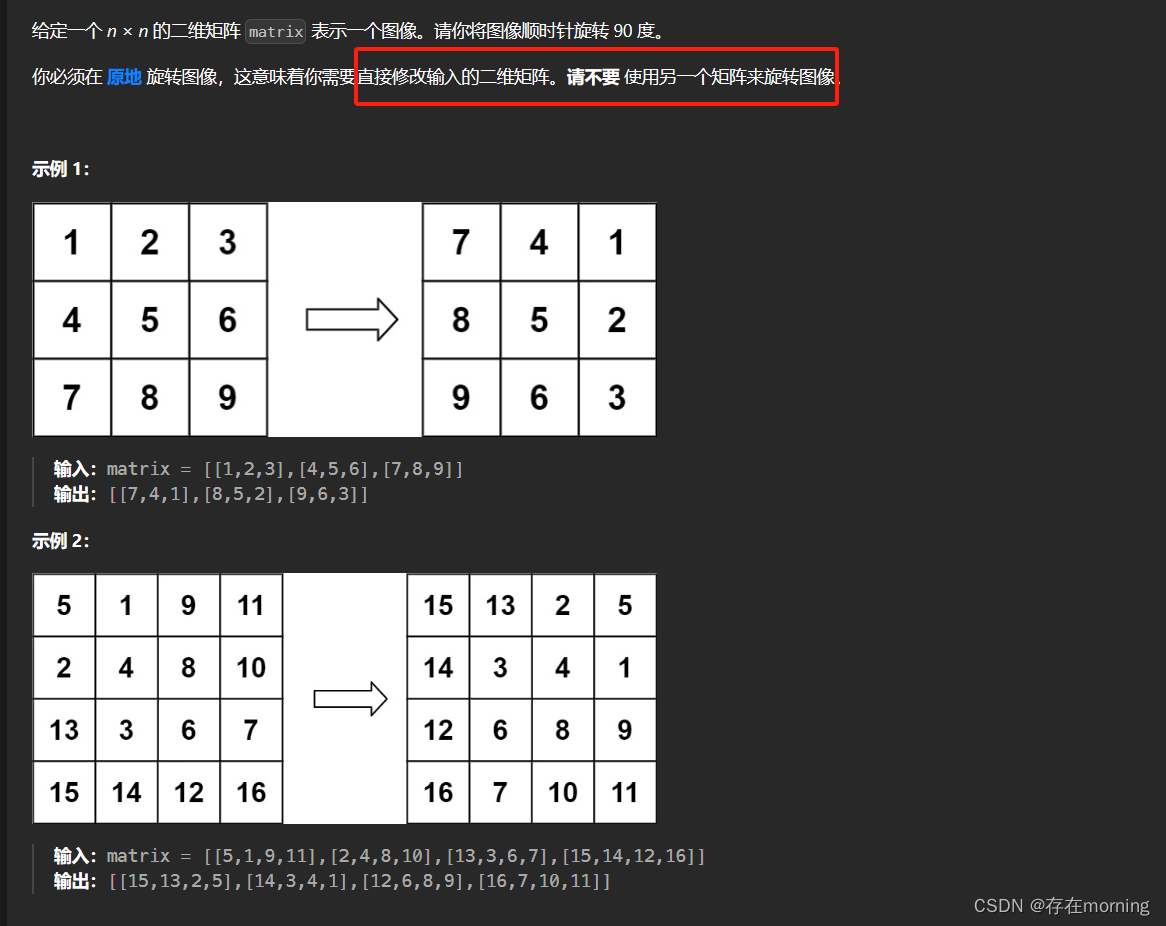
题干
解题思路
由原题知整体的旋转公式如下:

如果可以使用辅助矩阵则按如下方式修改即可:
class Solution {public void rotate(int[][] matrix) {int n = matrix.length;// 深拷贝 matrix -> tmpint[][] tmp = new int[n][];for (int i = 0; i < n; i++)tmp[i] = matrix[i].clone();// 根据元素旋转公式,遍历修改原矩阵 matrix 的各元素for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {matrix[j][n - 1 - i] = tmp[i][j];}}}
}
考虑不借助辅助矩阵,通过在原矩阵中直接「原地修改」,实现空间复杂度 **O(1)**的解法。以位于矩阵四个角点的元素为例,设矩阵左上角元素 A 、右上角元素 B 、右下角元素 C 、左下角元素 D 。矩阵旋转 90º 后,相当于依次先后执行 D→A,C→D, B→C, A→B 修改元素,即如下「首尾相接」的元素旋转操作:

如上图所示,由于第 1 步 D→A已经将 A覆盖(导致 A 丢失),此丢失导致最后第 4步 A→B无法赋值。为解决此问题,考虑借助一个「辅助变量 tmp」预先存储 A ,此时的旋转操作变为:
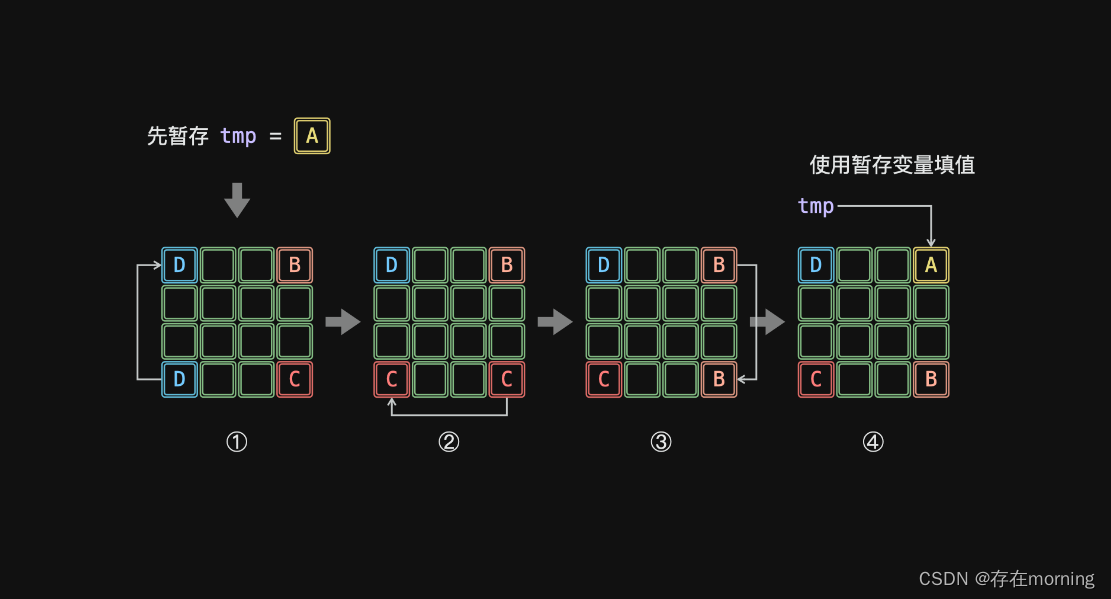
如上图所示,一轮可以完成矩阵 4 个元素的旋转。因而,只要分别以矩阵左上角 1/4的各元素为起始点执行以上旋转操作,

将这些元素旋转完成即完成了整个数组的旋转

具体来看,当矩阵大小n为偶数时,行列均取前n/2,当矩阵大小为奇数时,行取n/2,列取(n+1)/2,因为为奇数时,中间的元素不需要旋转
代码实现
基本数据结构:数组
辅助数据结构:无
算法:无
技巧:无
class Solution {public void rotate(int[][] matrix) {// 1 获取数组长度,依据替换顺序位置matrix[i][j]->matrix[j][n-1-i]推导出ABCD位置int n = matrix.length;//int a=matrix[i][j];int b=matrix[j][n-1-i];int c=matrix[n-1-i][n-1-j];int d=matrix[n-1-j][i];// 2 遍历行列,行取n/2,列取(n+1)/2 为了应对奇数长度的nfor (int i = 0; i < n / 2; i++) {for (int j = 0; j < (n + 1) / 2; j++) {// 2-1 暂存A的位置,用来后续替换Bint temp = matrix[i][j];// 2-2 D替换Amatrix[i][j] = matrix[n - 1 - j][i];// 2-3 C替换Dmatrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j];// 2-4 B替换Cmatrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i];// 2-5 A替换Bmatrix[j][n - 1 - i] = temp;}}}
}
复杂度分析
时间复杂度 O(N*N): 其中 N 为输入矩阵的行(列)数。需要将矩阵中每个元素旋转到新的位置,即对矩阵所有元素操作一次,使用O(N*N)的时间
空间复杂度 O(1) : 临时变量 tmp使用常数大小的额外空间。值得注意,当循环中进入下轮迭代,上轮迭代初始化的 tmp占用的内存就会被自动释放,因此无累计使用空间。
搜索二维矩阵【MID】
从下题矩阵的特性入手进行查找
题干

解题思路
数组从左到右和从上到下都是升序的,如果从右上角出发开始遍历呢?会发现每次都是向左数字会变小,向下数字会变大,有点和二分查找树相似。二分查找树的话,是向左数字变小,向右数字变大。所以我们可以把 target 和当前值比较。
- 如果 target 的值大于当前值,那么就向下走。
- 如果 target 的值小于当前值,那么就向左走。
- 如果相等的话,直接返回 true 。
也可以换个角度思考
- 如果 target 的值大于当前值,也就意味着当前值所在的行肯定不会存在 target 了,可以把当前行去掉,从新的右上角的值开始遍历。
- 如果 target 的值小于当前值,也就意味着当前值所在的列肯定不会存在 target 了,可以把当前列去掉,从新的右上角的值开始遍历。
看下边的例子
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]如果 target = 9,如果我们从 15 开始遍历, cur = 15target < 15, 去掉当前列, cur = 11
[1, 4, 7, 11],
[2, 5, 8, 12],
[3, 6, 9, 16],
[10, 13, 14, 17],
[18, 21, 23, 26] target < 11, 去掉当前列, cur = 7
[1, 4, 7],
[2, 5, 8],
[3, 6, 9],
[10, 13, 14],
[18, 21, 23] target > 7, 去掉当前行, cur = 8
[2, 5, 8],
[3, 6, 9],
[10, 13, 14],
[18, 21, 23] target > 8, 去掉当前行, cur = 9, 遍历结束
[3, 6, 9],
[10, 13, 14],
[18, 21, 23]
代码实现
基本数据结构:数组
辅助数据结构:无
算法:无
技巧:无
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可*** @param target int整型* @param array int整型二维数组* @return bool布尔型*/public boolean Find (int target, int[][] array) {// 1 入参判断if (array.length < 1) {return false;}// 2 定义行列边界,从右上角出发,所以初始化为右上角位置int right = array[0].length - 1;int top = 0;// 3 出发开始遍历,明确左右边界的范围while (right >= 0 && top <= array.length - 1) {int curValue = array[top][right];if (curValue > target) {// 3-1 如果当前值大于目标值,舍弃本列right--;} else if (curValue < target) {// 3-2 如果当前值小于目标值,舍弃本行top++;} else {// 3-3 如果当前值等于目标值,找到了目标值return true;}}return false;}
}
复杂度分析
- 时间复杂度 O(M+N) : 只遍历了一遍
- 空间复杂度 O(1) :没有使用额外空间。
拓展知识:二维数组
二维数组是一种常见的数据结构,它由多行和多列组成,可以用来存储和处理二维数据集合,例如矩阵、表格、图像、地图等。在不同的编程语言中,定义和使用二维数组的方式可能有所不同,以下是一些常见编程语言中的示例。
C/C++:
// 定义一个3x3的整数二维数组
int matrix[3][3] = {{1, 2, 3},{4, 5, 6},{7, 8, 9}
};// 访问元素
int element = matrix[1][2]; // 获取第二行第三列的元素,值为6
Python:
# 定义一个3x3的整数二维数组(使用嵌套列表)
matrix = [[1, 2, 3],[4, 5, 6],[7, 8, 9]
]# 访问元素
element = matrix[1][2] # 获取第二行第三列的元素,值为6
Java:
// 定义一个3x3的整数二维数组
int[][] matrix = {{1, 2, 3},{4, 5, 6},{7, 8, 9}
};// 访问元素
int element = matrix[1][2]; // 获取第二行第三列的元素,值为6
常用方法和操作:
-
访问元素: 使用索引来访问二维数组中的特定元素,例如
matrix[i][j],其中i表示行号,j表示列号。 -
遍历二维数组: 使用嵌套循环来遍历二维数组,通常使用一个循环迭代行,另一个循环迭代列,以访问所有元素。
-
初始化: 在定义二维数组时,可以初始化数组的值。可以使用嵌套列表(Python)、嵌套数组(C/C++)或类似方式来初始化。
-
修改元素: 可以通过索引来修改特定元素的值,例如
matrix[i][j] = newValue。 -
获取数组的行数和列数: 可以使用数组的长度或大小来获取行数和列数。
-
在算法中使用: 二维数组在解决各种问题时非常有用,例如矩阵运算、图算法、迷宫求解等。
-
释放内存(C/C++): 在使用动态分配内存创建二维数组时,需要谨慎释放内存以防止内存泄漏。
二维数组是一种非常灵活和强大的数据结构,可以在各种应用中发挥作用,从简单的数据存储到复杂的算法实现。
相关文章:

【算法训练-数组 三】【数组矩阵】螺旋矩阵、旋转图像、搜索二维矩阵
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是螺旋矩阵,使用【二维数组】这个基本的数据结构来实现 螺旋矩阵【EASY】 二维数组的结构特性入手 题干 解题思路 根据题目示例 mat…...

LED灯实验--汇编
asm-led.S .text .global _start _start: /* 1. led灯的初始化 *//* 1.1 使能GPIOE、DPIOF外设控制器的时钟 */ldr r0, 0x50000A28ldr r1, [r0]orr r1, r1, #(0x3 << 4)str r1, [r0]/* 1.2 设置PE10、PE8、PF10引脚为输出模式 */ldr r0, 0x50006000ldr r1, [r0]bic r1,…...

Android多线程学习:线程池(一)
一、概念 线程池:创建并维护一定数量的空闲线程,当有需要执行的任务,就交付给线程池中的一个线程,任务执行结束后,该线程也不会死亡,而是回到线程池中重新变为空闲状态。 线程池优点: 1、重用…...

网络安全(黑客技术)—小白自学笔记
1.网络安全是什么 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 2.网络安全市场 一、是市场需求量高; 二、则是发展相对成熟入…...

掌握核心技巧就能创建完美的目录!如何在Word中自动创建目录
目录是Word布局的一个重要因素,尤其是在编写较长的文档时。那么,你如何在你的作品中添加目录呢?在这篇文章中,我将分享一些基于Word2016自动创建目录的经验。希望它能或多或少地帮到你。 自动创建目录 1、输入目录文本的名称&am…...

正则表达式中re.match、re.search、re.findall的用法和区别
这位作者的例子写的非常好,记录一下,目前用到的比较多的是findall 正则表达式中re.match、re.search、re.findall的用法和区别_<re.match object; span(0, 270), match<a href"/-CSDN博客...
算法题:买卖股票的最佳时机含手续费(动态规划解法贪心解法-详解)
这道题有两种解法:动态规划 or 贪心算法。 贪心算法的提交结果要比动态规划好一些,总体上动态规划的解法更容易想到。(完整题目附在了最后) 1、动态规划解法 设置两个数,dp[0]表示遍历到股票prices[i]时手里没有股…...

【gcc】RtpTransportControllerSend学习笔记 4:码率分配
本文是woder大神 的文章的学习笔记。 大神的webrtc源码分析(8)-拥塞控制(上)-码率预估 详尽而具体,堪称神作。 gcc保障带宽公平性,预估码率后要分配码率,实现qos效果: webrtc源码分析(9)-拥塞控制(下)-码率分配 是 woder 大神进一步给出的另一篇神作。 本文是对(https://w…...

「专题速递」AR协作、智能NPC、数字人的应用与未来
元宇宙是一个融合了虚拟现实、增强现实、人工智能和云计算等技术的综合概念。它旨在创造一个高度沉浸式的虚拟环境,允许用户在其中交互、创造和共享内容。在元宇宙中,人们可以建立虚拟身份、参与虚拟社交,并享受无限的虚拟体验。 作为互联网大…...

什么是基于意图的网络(IBN)
基于意图的网络是一种网络技术,它根据业务意图(来自网络管理员的服务请求)配置 IT 基础架构,无需任何人工干预,它不断提供关键的网络见解,并不断调整硬件配置以确保满足意图,它将网络从以设备为…...
知识增强语言模型提示 零样本知识图谱问答10.8
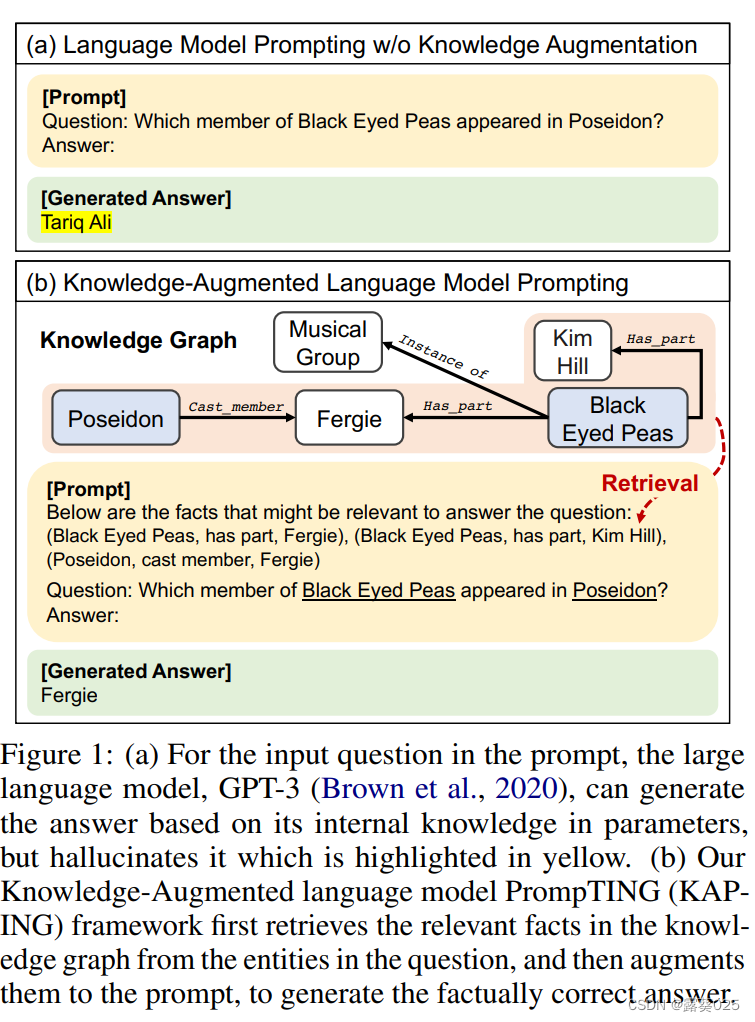
知识增强语言模型提示 零样本知识图谱问答 摘要介绍相关工作方法零样本QA的LM提示知识增强的LM提示与知识问题相关的知识检索 摘要 大型语言模型(LLM)能够执行 零样本closed-book问答任务 ,依靠其在预训练期间存储在参数中的内部知识。然而&…...

虚拟现实项目笔记:SDK、Assimp、DirectX Sample Browser、X86和X64
文章目录 SDK是什么Assimp是什么DirectX Sample Browser是什么X86和X64生成解决方案和重新生成解决方案 SDK是什么 SDK是Software Development Kit的英文缩写,意思是软件开发包。 软件开发包中往往包含有多种辅助进行软件开发的内容,包括一些软件开发工…...
openwrt rm500u ncm方式拨号步骤记录
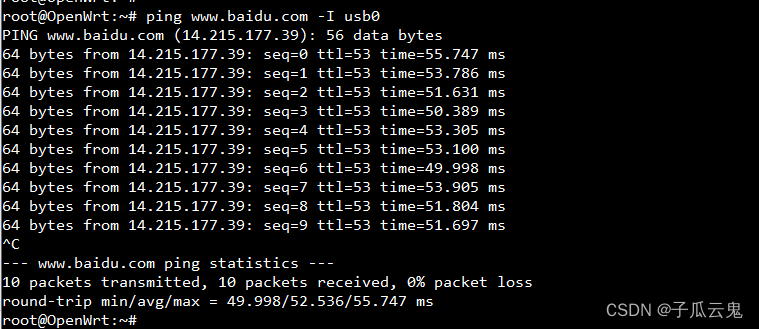
1.进入设备页面 用户名:root 2.创建接口 3.配置接口 国内APN 信息 中国移动APN:CMNET 中国联通APN:3GNET 中国电信APN:CTNET 4.防火墙配置 5.点击Save&Apply 6.配置完成后重启设备。重新进入设备页面,可以看…...

使用js代码将一个值为“1=增量,2=全量“的字符串转化为一个数组,数据格式为[{value:““,label:“‘‘}]
const str "1增量,2全量"; const arr str.split(",").map(item > {const [value, label] item.split("");return { value, label}; });...

图片调色盘
图片预览 配置安装 Color-Thief 安装包使用文档 yarn add colorthief -S // npm install colorthief --save代码 <template><div class"img-thief"><div class"container"><div class"thief-item" v-for"(item, in…...
一文读懂Base64
这几天在和第三方交互的时候,对方返回的数据是base64格式的数据,所以这两天又彻底捋了下Base64的来龙去脉。之前看过一篇文章说的非常好(再找到给加上链接),我在这不详细说明了,只说转换过程。 还是使用中…...

CCF CSP认证 历年题目自练 Day20
题目一 试题编号: 201903-1 试题名称: 小中大 时间限制: 1.0s 内存限制: 512.0MB 问题描述: 题目分析(个人理解) 常规题目,先看输入,第一行输入n表示有多少数字&am…...

【Overload游戏引擎分析】从视图投影矩阵提取视锥体及overload对视锥体的封装
overoad代码中包含一段有意思的代码,可以从视图投影矩阵逆推出摄像机的视锥体,本文来分析一下原理 一、平面的方程 视锥体是用平面来表示的,所以先看看平面的数学表达。 平面方程可以由其法线N(A, B, C)和一个点Q(x0,…...

vue全局事件总线是什么?有什么用?解决了什么问题,与pinia有什么区别?
全局事件总线快速入门 概念基本概念(是什么?)核心概念 核心特性和优势(有什么用?)解决了什么问题?主要优势是什么? 案例演示?传递数据-案例演示传递事件-案例演示 与pinia有什么区别?…...
【debian 12】:debian系统切换中文界面
目录 目录 项目场景 基础参数 原因分析 解决方案 1.ctrlaltT 打开终端 2.查询当前语言环境(我的已经设置成了中文 zh_CN.UTF-8) 3.打开语言配置界面 4.最后一步:重启 不要放弃任何一个机会! 项目场景: 这两…...
:手搓截屏和帧率控制)
Python|GIF 解析与构建(5):手搓截屏和帧率控制
目录 Python|GIF 解析与构建(5):手搓截屏和帧率控制 一、引言 二、技术实现:手搓截屏模块 2.1 核心原理 2.2 代码解析:ScreenshotData类 2.2.1 截图函数:capture_screen 三、技术实现&…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...
