C/C++学习 -- RSA算法
概述
RSA算法是一种广泛应用于数据加密与解密的非对称加密算法。它由三位数学家(Rivest、Shamir和Adleman)在1977年提出,因此得名。RSA算法的核心原理是基于大素数的数学问题的难解性,利用两个密钥来完成加密和解密操作。
特点
RSA算法的特点如下:
非对称性:RSA算法使用一对公钥和私钥,其中公钥用于加密,私钥用于解密。这种非对称性使得通信双方可以安全地交换信息,而不需要共享密钥。
安全性:RSA的安全性基于大素数的难解性,即大整数分解问题。目前尚无有效的算法能够在合理的时间内分解大素数,因此RSA算法被认为是安全的。
适用性广泛:RSA算法广泛用于数字签名、数据加密、密钥交换等领域,被广泛应用于网络通信、电子商务等场景。
效率相对较低:由于涉及大数运算,RSA算法相对于对称加密算法而言,加解密速度较慢。因此,通常仅用于加密短文本或用于安全交换对称密钥。
原理
RSA算法的核心原理基于以下数学概念:
选择两个大素数:选择两个足够大的不同素数p和q。
计算n和Φ(n):计算n = p * q 和Φ(n) = (p-1) * (q-1)。
选择公钥和私钥:选择一个公钥e,满足1 < e < Φ(n),且e与Φ(n)互质。然后,计算私钥d,满足d * e ≡ 1 (mod Φ(n))。
加密:使用公钥(e, n)对明文进行加密,得到密文c = m^e (mod n),其中m为明文。
解密:使用私钥(d, n)对密文进行解密,得到明文m = c^d (mod n)。
C语言实现RSA算法
以下是一个简单的C语言实现RSA算法的示例代码。请注意,这只是一个基本的示例,实际应用中需要考虑更多的安全性和性能优化。
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
// 欧几里得算法求最大公约数
int gcd(int a, int b) {if (b == 0) return a;return gcd(b, a % b);
}
// 计算模反函数
int mod_inverse(int e, int phi) {int d;for (d = 2; d < phi; d++) {if ((e * d) % phi == 1) {return d;}}return -1; // 如果找不到模反函数
}
int main() {int p = 61;int q = 53;int n = p * q;int phi = (p - 1) * (q - 1);int e = 17; // 选择一个合适的公钥int d = mod_inverse(e, phi); // 计算私钥int plaintext = 42;int ciphertext = (int)pow(plaintext, e) % n;int decrypted_text = (int)pow(ciphertext, d) % n;printf("明文:%d\n", plaintext);printf("密文:%d\n", ciphertext);printf("解密后的明文:%d\n", decrypted_text);return 0;
}C++语言实现RSA算法
以下是一个简单的C++语言实现RSA算法的示例代码,使用了C++的标准库以及大数库(例如OpenSSL)来处理大整数运算。
#include <iostream>
#include <openssl/rsa.h>
#include <openssl/pem.h>
int main() {// 生成RSA密钥对RSA *rsa = RSA_generate_key(2048, RSA_F4, nullptr, nullptr);// 明文const char *plaintext = "Hello, RSA!";// 分配内存来保存密文和解密后的文本unsigned char *ciphertext = (unsigned char *)malloc(RSA_size(rsa));unsigned char *decrypted_text = (unsigned char *)malloc(RSA_size(rsa));// 加密int ciphertext_len = RSA_public_encrypt(strlen(plaintext), (const unsigned char *)plaintext, ciphertext, rsa, RSA_PKCS1_PADDING); // 解密int decrypted_text_len = RSA_private_decrypt(ciphertext_len, ciphertext, decrypted_text, rsa, RSA_PKCS1_PADDING);// 打印结果printf("明文:%s\n", plaintext);printf("密文:");for (int i = 0; i < ciphertext_len; i++) {printf("%02X ", ciphertext[i]);}printf("\n");printf("解密后的明文:%s\n", decrypted_text);// 释放内存RSA_free(rsa);free(ciphertext);free(decrypted_text);return 0;
}请注意,实际应用中,需要更多的错误处理和安全性考虑。此示例仅用于演示RSA算法的基本原理和实现方法。在实际应用中,建议使用现有的密码库来执行RSA加密。
相关文章:

C/C++学习 -- RSA算法
概述 RSA算法是一种广泛应用于数据加密与解密的非对称加密算法。它由三位数学家(Rivest、Shamir和Adleman)在1977年提出,因此得名。RSA算法的核心原理是基于大素数的数学问题的难解性,利用两个密钥来完成加密和解密操作。 特点 …...
基于若依ruoyi-nbcio支持flowable流程增加自定义业务表单(一)
因为需要支持自定义业务表单的相关流程,所以需要建立相应的关联表 1、首先先建表wf_custom_form -- ---------------------------- -- Table structure for wf_custom_form -- ---------------------------- DROP TABLE IF EXISTS wf_custom_form; CREATE TABLE wf…...

面试经典 150 题 1 —(数组 / 字符串)— 88. 合并两个有序数组
88. 合并两个有序数组 方法一: class Solution { public:void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {for(int i 0; i<n;i){nums1[mi] nums2[i];}sort(nums1.begin(),nums1.end());} };方法二: clas…...

【大数据 | 综合实践】大数据技术基础综合项目 - 基于GitHub API的数据采集与分析平台
🤵♂️ 个人主页: AI_magician 📡主页地址: 作者简介:CSDN内容合伙人,全栈领域优质创作者。 👨💻景愿:旨在于能和更多的热爱计算机的伙伴一起成长!!&…...
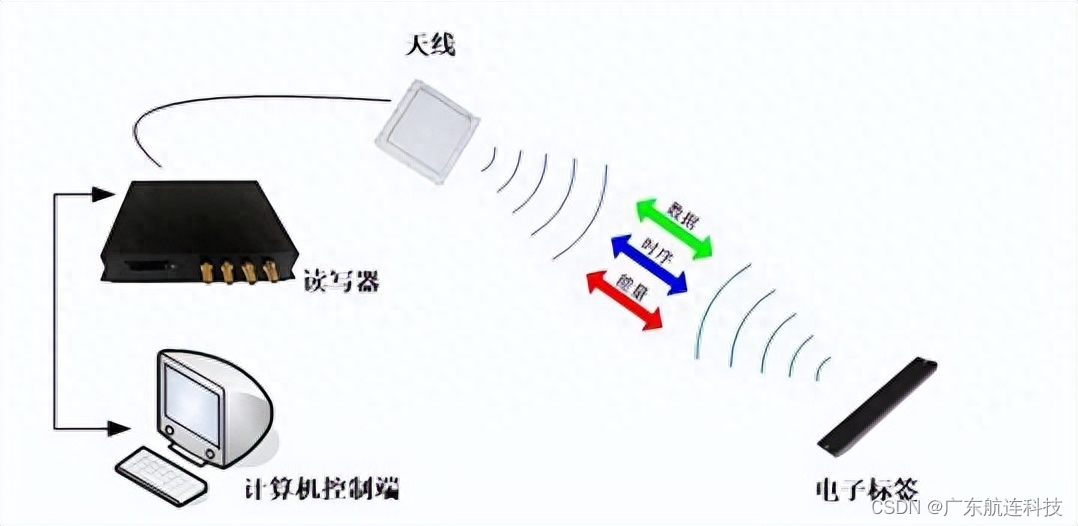
超高频RFID模具精细化生产管理方案
近二十年来,我国的模具行业经历了快速发展的阶段,然而,模具行业作为一个传统、复杂且竞争激烈的行业,企业往往以订单为导向,每个订单都需要进行新产品的开发,从客户需求分析、结构确定、报价、设计、物料准…...

FP-Growth算法全解析:理论基础与实战指导
目录 一、简介什么是频繁项集?什么是关联规则挖掘?FP-Growth算法与传统方法的对比Apriori算法Eclat算法 FP树:心脏部分 二、算法原理FP树的结构构建FP树第一步:扫描数据库并排序第二步:构建树 挖掘频繁项集优化&#x…...

Jmeter 分布式压测,你的系统能否承受高负载?
你可以使用 JMeter 来模拟高并发秒杀场景下的压力测试。这里有一个例子,它模拟了同时有 5000 个用户,循环 10 次的情况。 请求默认配置 token 配置 秒杀接口 结果分析 但是,实际企业中,这种压测方式根本不满足实际需求。下…...

什么是浮动密封?
浮动密封也称为机械面密封或双锥密封,是一种用于各种行业和应用的特殊类型的密封装置。它旨在提供有效的密封和保护,防止污染物的进入以及旋转设备中润滑剂或液体的润滑剂泄漏。 浮动密封件由相同的金属环组成,这些金属环称为密封环…...

浅析前端单元测试
对于前端来说,测试主要是对HTML、CSS、JavaScript进行测试,以确保代码的正常运行。 常见的测试有单元测试、集成测试、端到端(e2e)的测试。 单元测试:对程序中最小可测试单元进行测试。我们可以类比对汽车的测试&…...

线上mysql表字段加不了Fail to get MDL on replica during DDL synchronize,排查记录
某天接近业务高峰期想往表里加字段加不了,报错:Fail to get MDL on replica during DDL synchronize 遂等到业务空闲时操作、还是加不了, 最后怀疑是相关表被锁了,或者有事务一直进行(可能这俩是一个意思)&…...
vue3使用element plus的时候组件显示的是英文
问题截图 这是因为国际化导致的 解决代码 import zhCn from "element-plus/es/locale/lang/zh-cn"; 或者 import zhCn from "element-plus/lib/locale/lang/zh-cn";const localezhCn<el-config-provider :locale"locale"><el-date-pic…...
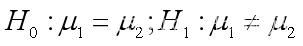
Matlab参数估计与假设检验(举例解释)
参数估计分为点估计和区间估计,在matlab中可以调用namefit()函数来计算参数的极大似然估计值和置信区间。而数据分析中用得最多的是正态分布参数估计。 例1 从某厂生产的滚珠中抽取10个,测得滚珠的直径(单位:mm)为x[…...

qt响应全局热键
QT5 QWidget响应全局热键-百度经验...

android 代码设置静态Ip地址的方法
在Android中,可以使用以下代码示例来设置静态IP地址: import android.content.Context import android.net.ConnectivityManager import android.net.LinkAddress import android.net.Network import android.net.NetworkCapabilities import android.ne…...
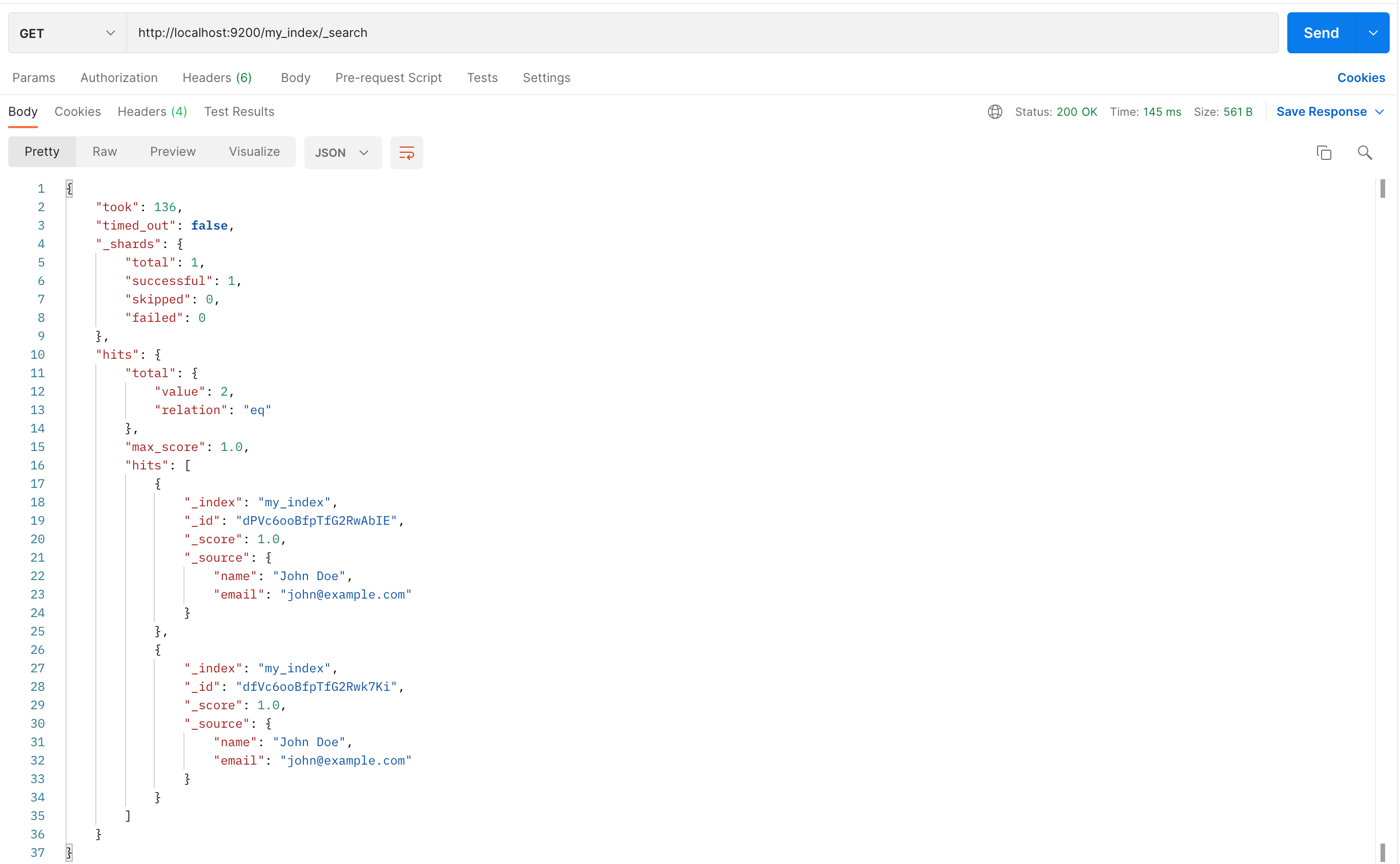
Elasticsearch安装访问
Elasticsearch 是一个开源的、基于 Lucene 的分布式搜索和分析引擎,设计用于云计算环境中,能够实现实时的、可扩展的搜索、分析和探索全文和结构化数据。它具有高度的可扩展性,可以在短时间内搜索和分析大量数据。 Elasticsearch 不仅仅是一个…...
:setState为什么使用异步机制?)
面试题-React(十):setState为什么使用异步机制?
在React中,setState的异步特性和异步渲染机制是开发者们经常讨论的话题。为什么React选择将setState设计为异步操作?异步渲染又是如何实现的?本篇博客将深入探究这些问题,通过代码示例解释为什么异步操作是React的一大亮点。 一、…...
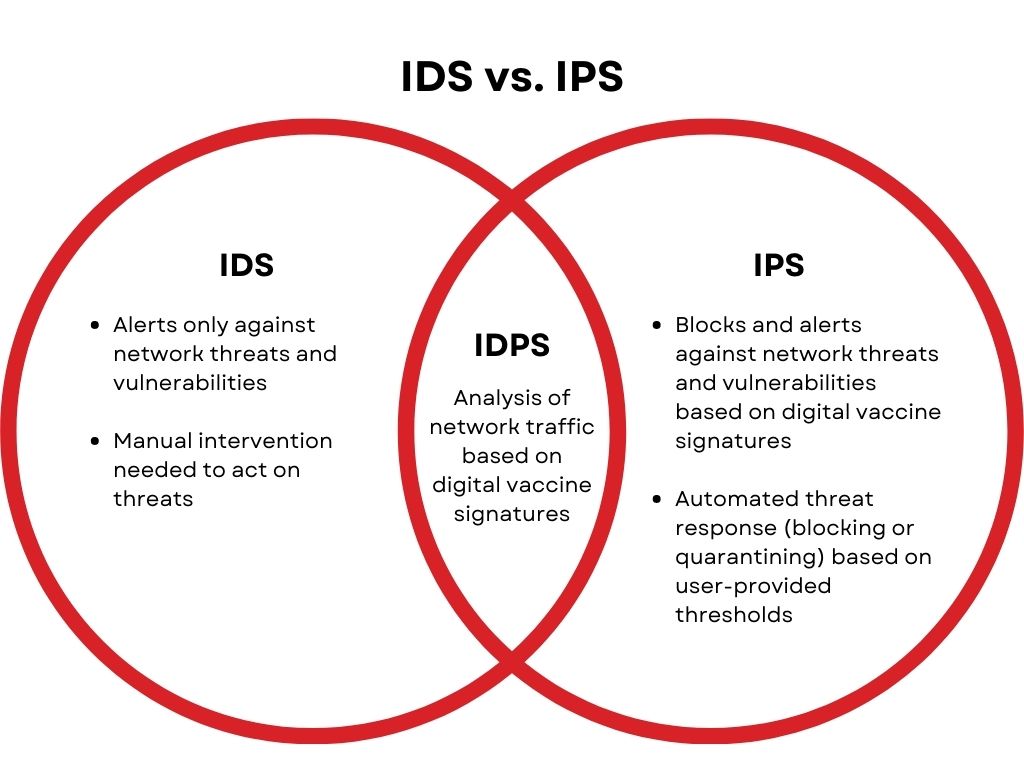
入侵防御系统(IPS)网络安全设备介绍
入侵防御系统(IPS)网络安全设备介绍 1. IPS设备基础 IPS定义 IPS(Intrusion Prevention System)是一种网络安全设备或系统,用于监视、检测和阻止网络上的入侵尝试和恶意活动。它是网络安全架构中的重要组成部分&…...

【Linux基础】Linux的基本指令使用(超详细解析,小白必看系列)
👉系列专栏:【Linux基础】 🙈个人主页:sunnyll 目录 💦 ls 指令 💦 pwd指令 💦cd指令 💦touch指令 💦mkdir指令(重要) 💦rmdir指令…...

【无标题】Test
短视频平台的那些事 前言 过去几年,我一直专注于短视频平台的建设和开发工作。在这个过程中,我发现这个领域有着非常多的挑战和机遇,也涌现出了许多新的技术和创新。今天大家分享我个人的一些经验,希望能够为大家带来一些启发和帮…...

1576. 替换所有的问号
1576. 替换所有的问号 C代码:自己写的 char * modifyString(char * s){int n strlen(s);for (int i 0; i < n; i){if (s[i] ?) {if (i ! 0 && i ! n-1) {for (int j 0; j < 26; j) {if (a j ! s[i-1] && a j ! s[i1]) {s[i] a j;br…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...
