pytorch_神经网络构建1
文章目录
- pytorch简介
- 神经网络基础
- 分类问题分析:逻辑回归模型
- 逻辑回归实现
- 多层神经网络
- 多层网络搭建
- 保存模型
pytorch简介
为什么神经网络要自定义数据类型torch.tensor?
tensor可以放在gpu上训练,支持自动求导,方便快速训练,同时支持numpy的运算,是加强版,numpy不支持这些
为什么要求导?
导数是真实值和预测值的误差函数下降最快的地方,根据求导可以快速降低误差值,让真实值和预测值贴合



神经网络基础
监督学习:已经打标记的样本进行训练,然后预测
非监督学习:对一些无标记数据进行结构化分类,发现潜在的规律
强化学习:一个机器不断根据新的输入做出决策,然后根据结果进行奖惩来学习
线性模型:y=wx+b,w就是要优化的值,我们要根据损失值来不断优化w让他的预测贴近真实值
这需要知道loss函数,(真实值和预测值之间的误差),然后根据loss函数的反馈优化w降低loss
当loss求和最小的时候可以得出预测越来越准
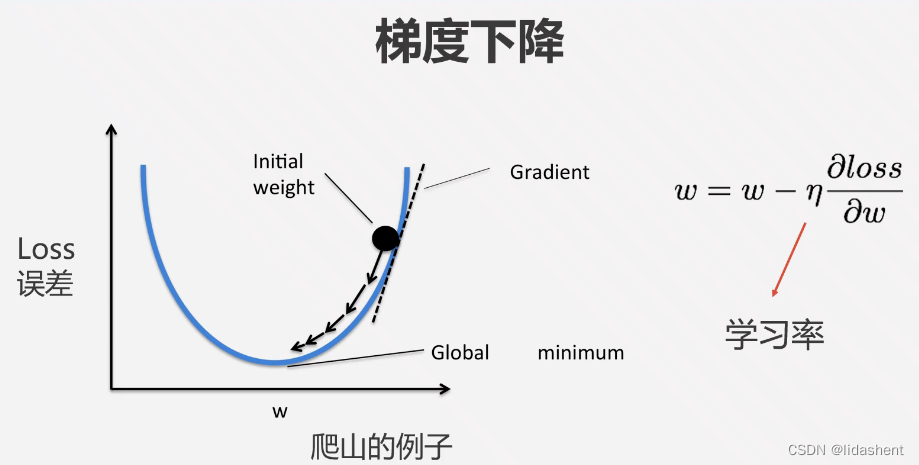
为了减少loss就需要知道loss在哪个方向下降的最快,这就是求导,梯度下降算法

更直观一点是让loss下降的更快,以至于降到最低,让真实值和预测值无限贴合,
学习率代表了斜率变化的步长,合理的设置会方便于我们找到最优w,错误的设置过大过小会导致预测值无法贴合真实值
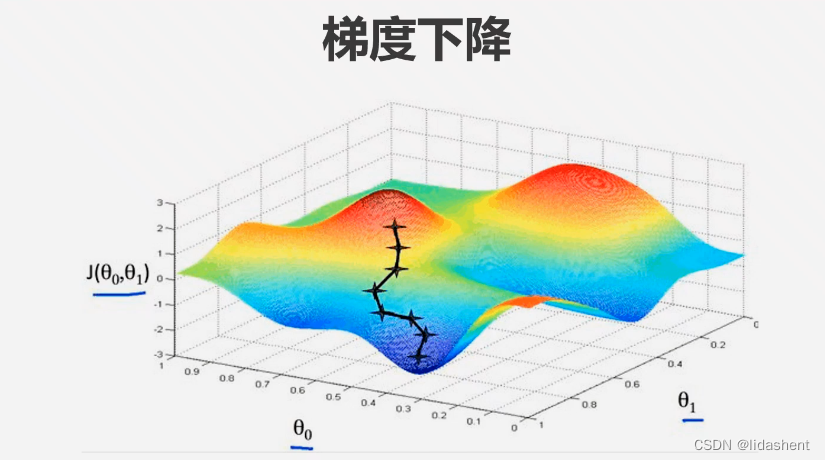
在三维和多维度图象上更容易理解这一点
当有三个维度的数据时更加直观
那么构建模型流程如下
定义参数,定义损失函数,定义网络模型,这里为线性模型,然后根据损失函数优化参数w让线性模型拟合的更好
理解线性模型对未来的深层模型构建有很大帮助
我们定义一些点,然后用线性模型拟合这些数据
x_train np.array([[3.3],[4.4],[5.5],[6.71],[6.93],[4.168],[9.779],[6.182],[7.59],[2.167],[7.042],[10.791],[5.313],[7.997],[3.1]],dtype=np.float32)
y_train =np.array([[1.7],[2.76],[2.09],[3.19],[1.694],[1.573],[3.366],[2.596],[2.53],[1.221],[2.827],[3.465],[1.65],[2.904],[1.3]],dtype=np.float32)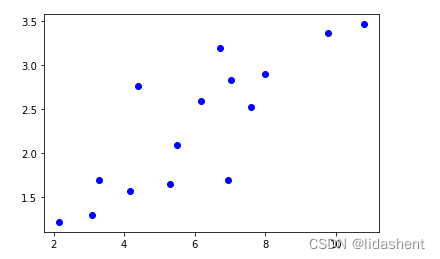
然后将这些数据转化为tensor类型,定义参数wb,使用正态分布随机初始化数据wb,定义网络模型,损失函数模型
损失函数模型计算误差方式为求平方差之和
x_train =torch.from_numpy(x_train)
y_train =torch.from_numpy(y_train)
w1=Variable(torch.randn(1),requires_grad=True)
b1=Variable(torch.zeros(1),requires_grad=True)
def linear_model(x):return x*w1+b1
def get_loss(y_,y):return torch.mean((y_-y_train)**2)
y_=linear_model(x_train)
loss=get_loss(y_,y_train)
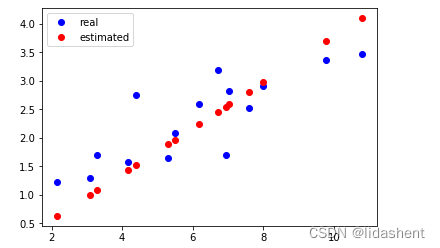
画出初始化后的预测图形为:这肯定不对的,然后对其进行优化
plt.plot(x_train.data.numpy(), y_train.data.numpy(), 'bo', label='real')
plt.plot(x_train.data.numpy(), y_.data.numpy(), 'ro', label='estimated')
plt.legend()
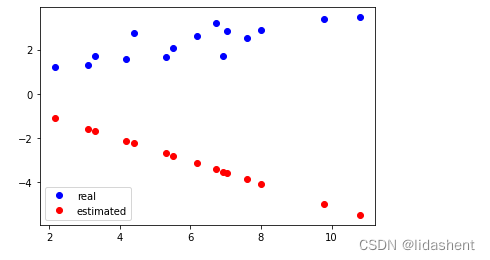
进行10次迭代
获得预测值,计算误差,将之前的梯度归零,计算新的梯度,根据新的梯度对参数wb进行优化
for e in range(10): # 进行 10 次更新y_ = linear_model(x_train)loss = get_loss(y_, y_train)w.grad.zero_() # 记得归零梯度b.grad.zero_() # 记得归零梯度loss.backward()w.data = w.data - 1e-2 * w.grad.data # 更新 wb.data = b.data - 1e-2 * b.grad.data # 更新 b print('epoch: {}, loss: {}'.format(e, loss.data[0]))
使用的是科学计数法,1e相当于10,科学记数法以x*10^n将所有数据进行分解,1e-2就是10的负二次方.0.01
梯度归零的意义在于得到新的梯度前清空上一次计算的梯度,对新的梯度进行优化
然而实际上,参数点往往分布的并不规律,也不可能仅仅用wx+b就可以拟合,
我们来设计一个新的图像
y = x+x2+x3+b
# 画出这个函数的曲线
x_sample = np.arange(-3, 3.1, 0.1)
y_sample = b_target[0] + w_target[0] * x_sample + w_target[1] * x_sample ** 2 + w_target[2] * x_sample ** 3
plt.plot(x_sample, y_sample, label='real curve')
plt.legend()
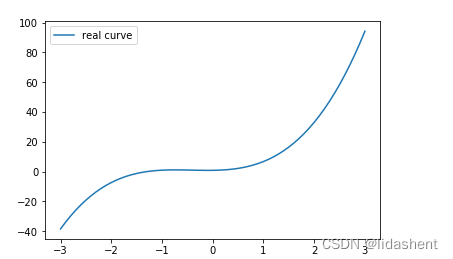
然后设置一些训练数据x和y
x为一个多行3列矩阵
x_train = np.stack([x_sample ** i for i in range(1, 4)], axis=1)
x_train = torch.from_numpy(x_train).float() # 转换成 float tensor
y_train = torch.from_numpy(y_sample).float().unsqueeze(1) # 转化成 float tensor
定义wb参数和神经网络模型,这里依旧为线性模型,损失函数,损失函数同wx+b模型依旧求平常差之和
# 定义参数和模型
w = Variable(torch.randn(3, 1), requires_grad=True)
b = Variable(torch.zeros(1), requires_grad=True)
# 将 x 和 y 转换成 Variable
x_train = Variable(x_train)
y_train = Variable(y_train)
def multi_linear(x):return torch.mm(x, w) + b
查看原始拟合图像
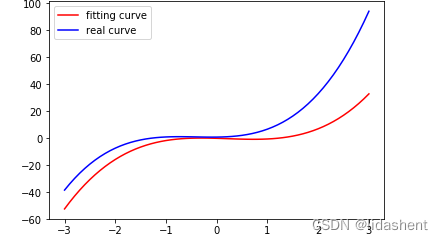
更新参数wb
# 进行 100 次参数更新
for e in range(100):y_pred = multi_linear(x_train)loss = get_loss(y_pred, y_train)w.grad.data.zero_()b.grad.data.zero_()loss.backward()w.data = w.data - 0.001 * w.grad.datab.data = b.data - 0.001 * b.grad.data
# 画出更新之后的结果
y_pred = multi_linear(x_train)plt.plot(x_train.data.numpy()[:, 0], y_pred.data.numpy(), label='fitting curve', color='r')
plt.plot(x_train.data.numpy()[:, 0], y_sample, label='real curve', color='b')
plt.legend()
画出拟合后的图形
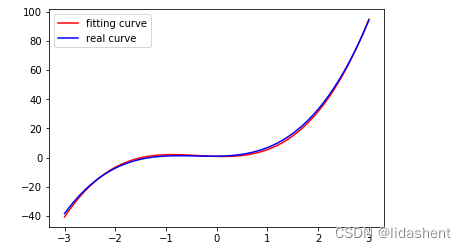
w = Variable(torch.randn(3, 1), requires_grad=True)
设置自变张量不可缺少
varable在pytorch0.4之后就不再使用,以后的torch自带梯度计算
上面是单w权重的情况,实际使用中往往是多权重,会有w1,2,3
但是写法不变
plt.plot(x_train.data.numpy()[:, 0], y_pred.data.numpy(), label='fitting curve',
color='r')
x_train.data.numpy()[:, 0]代表x_train所有行的第一个值x值
可以看到,对于线性模型只要模型设置正确,loss函数设置合理,就能够得到贴近值,这对于线性模型求解益处巨大,
然而有一类问题是线性问题不涉及的,那就是离散问题,无法用公式描述
分类问题分析:逻辑回归模型
他和上面的模型的区别在于多了一个sigmod函数,分类函数
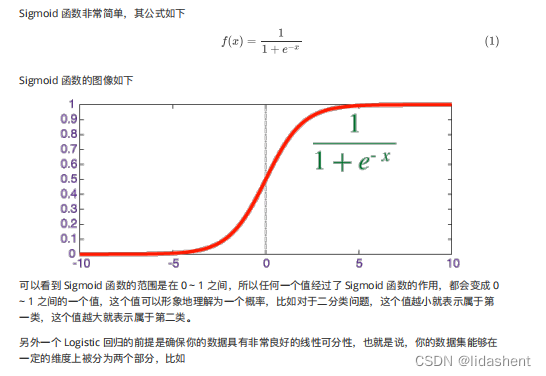
所有的y值都能够被放在-1到1的区间,这意味着可以把它看做概率,
分类问题和回归问题的区别在于回归问题是连续问题,比如拟合曲线,分类是离散问题,在解决问题前需要明白要解决的是那种问题
loss函数的变化:
既然是分类,输入任意数据经过sigmoid,a类概率为y_,b类概率为1-y_,如果输入的数据类型为a,则y_越大越好,1-y_越小越好
y_是概率值<=1
loss=-(y*log(y_)+(1-y)*log(1-y_))
输入的y只能为0,1
当输入0,0的概率损失函数loss=-(log(1-y_)).表示预测为假越大越好
当输入1,1的概率损失函数为loss=-(log(y_)),表示预测为真越大越好
当然log是有底数的,它的底数是e
逻辑回归实现
我们观察这些点的分布
# 从 data.txt 中读入点
with open('./data.txt', 'r') as f:data_list = [i.split('\n')[0].split(',') for i in f.readlines()]data = [(float(i[0]), float(i[1]), float(i[2])) for i in data_list]# 标准化
x0_max = max([i[0] for i in data])
x1_max = max([i[1] for i in data])
data = [(i[0]/x0_max, i[1]/x1_max, i[2]) for i in data]x0 = list(filter(lambda x: x[-1] == 0.0, data)) # 选择第一类的点
x1 = list(filter(lambda x: x[-1] == 1.0, data)) # 选择第二类的点plot_x0 = [i[0] for i in x0]
plot_y0 = [i[1] for i in x0]
plot_x1 = [i[0] for i in x1]
plot_y1 = [i[1] for i in x1]plt.plot(plot_x0, plot_y0, 'ro', label='x_0')
plt.plot(plot_x1, plot_y1, 'bo', label='x_1')
plt.legend(loc='best')
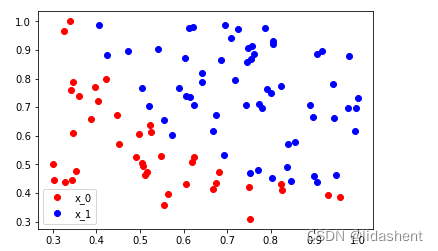
分布离散问题,使用逻辑回归来进行分类较为合适
torch.manual_seed(2000)
随机数种子,用于初始化模型参数,划分数据集,打乱数据等,有了初始值,则可以确保不同机器上,不同执行次数上模型初始化,数据初始化一致,实验结果具备可重复性
x0=list(filter(lambda x:x[-1] ==0.0,data))
filter传入一个lambda表达式,可迭代对象,返回一个迭代器,list将迭代器转化为list对象
对data中的行x进行迭代,找到每行最后元素等于0.0的行
plt.plot(plot_x1,plot_y1,"bo",label="x_1")
在坐标轴上画图,参数分别为x,y,颜色,标签
颜色ro红色,bo蓝色
plt.legend(loc='best')
选择最佳位置放置图像
那么延续之前线性模型的经验,我们需要设置wb,设置损失函数(这里不再求平方差而是求log),神经网络模型
对于sigmoid函数,
pytroch已经内置了这个函数,而且实现的速度更快,底层用c++编写,同时还有其他函数,直接调用即可
因此初始化wb和loss函数
np_data = np.array(data, dtype='float32') # 转换成 numpy array
x_data = torch.from_numpy(np_data[:, 0:2]) # 转换成 Tensor,大小是 [100, 2]
y_data = torch.from_numpy(np_data[:, -1]).unsqueeze(1) # 转换成 Tensor,大小是 [100, 1]
w = Variable(torch.randn(2, 1), requires_grad=True)
b = Variable(torch.zeros(1), requires_grad=True)
def sigmoid(x):return 1 / (1 + np.exp(-x))
def binary_loss(y_pred, y):logits = (y * y_pred.clamp(1e-12).log() + (1 - y) * (1 - y_pred).clamp(1e-12).log()).mean()return -logits
def logistic_regression(x):return F.sigmoid(torch.mm(x, w) + b)
将图像绘画出来如下
# 画出参数更新之前的结果
w0 = w[0].data[0]
w1 = w[1].data[0]
b0 = b.data[0]plot_x = np.arange(0.2, 1, 0.01)
plot_y = (-w0 * plot_x - b0) / w1plt.plot(plot_x, plot_y, 'g', label='cutting line')
plt.plot(plot_x0, plot_y0, 'ro', label='x_0')
plt.plot(plot_x1, plot_y1, 'bo', label='x_1')
plt.legend(loc='best')
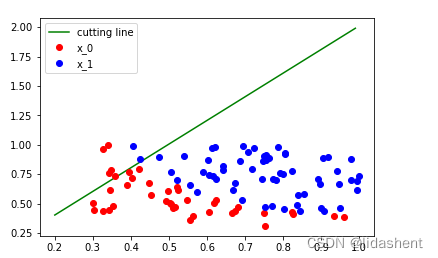
那么毫无疑问的,对于每一个坐标点[x,y]的分类是错误的,这里我们设置w的参数为2,生成两个w为xy加权重
但同时每次都手动更新一批wb是不合适的,应该做到w一次设置,自动更新,我们只关心w的数量和步长,手动调整w
变化不是我们应该关心的,我们需要一个w自动优化器
torch.optim接受一个nn.Parameter所定义的数据类型,然后自动对其中的所有数据进行更新维护
nn.Parameter默认带梯度,而Variable默认不带梯度
如果只是遍历更新参数似乎也并无必要,实际上optim带有众多参数优化器,比如SGD梯度下降方法来更新参数
这里设置学习率为1
以后更新参数只需要两行代码,不涉及具体参数操作
w=nn.Parameter(torch.randn(2,1))
b=nn.Parameter(torch.zeros(1))
optimizer=torch.optim.SGD([w,b],lr=1.)
for e in range(1000):# 前向传播y_pred = logistic_regression(x_data)loss = binary_loss(y_pred, y_data) # 计算 loss# 反向传播optimizer.zero_grad() # 使用优化器将梯度归 0loss.backward()optimizer.step() # 使用优化器来更新参数# 计算正确率mask = y_pred.ge(0.5).float()acc = (mask == y_data).sum().data[0] / y_data.shape[0]if (e + 1) % 200 == 0:print('epoch: {}, Loss: {:.5f}, Acc: {:.5f}'.format(e+1, loss.data[0], acc))
画出新分类图
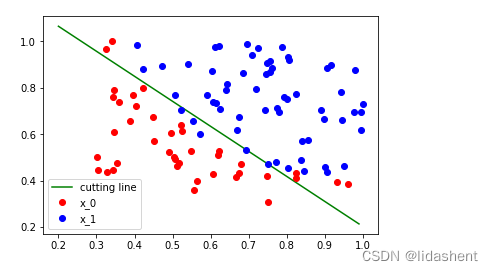
其实不仅仅w参数有优化器,对于loss函数也有优化器,这意味着对于常见的分类可以直接使用预设的优化器,而不用自己来实现,而且预设的优化器底层用c++实现,相比于我们自己写的效率更高
线性回归里,上一次使用的计算平方差的优化器函数为nn.MSE()
而逻辑回归里使用的二分类优化器函数为nn.BCEWithLogitsLoss(),这个损失函数优化器还集成了sigmoid,那么之前在计算真实值与推测值矩阵计算之后再进行的sigmoid得到概率操作就不用做了,直接调用这个函数输入预测值和真实值,得到的就是预测概率的损失值的和的平均值(原来的功能,都一样,更快而已)
得到loss优化器对象,计算损失值,在大型网络中预设的loss运行速度更为明显
# 使用自带的loss
criterion = nn.BCEWithLogitsLoss() # 将 sigmoid 和 loss 写在一层,有更快的速度、更好的稳定性
w = nn.Parameter(torch.randn(2, 1))
b = nn.Parameter(torch.zeros(1))
def logistic_reg(x):return torch.mm(x, w) + b
optimizer = torch.optim.SGD([w, b], 1.)
for e in range(1000):# 前向传播y_pred = logistic_reg(x_data)loss = criterion(y_pred, y_data)# 反向传播optimizer.zero_grad()loss.backward()optimizer.step()# 计算正确率mask = y_pred.ge(0.5).float()acc = (mask == y_data).sum().data[0] / y_data.shape[0]if (e + 1) % 200 == 0:print('epoch: {}, Loss: {:.5f}, Acc: {:.5f}'.format(e+1, loss.item(), acc))
一些补充:
- 当jupyter出现问题时重启一下也许就可以 代码过了保质期变得不可信任,文件不能加载,重新信任一下
为什么要将numpy数据转化为torch数据
因为torch数据被优化了,可以放在gpu上训练,支持自动求导,非常适合矩阵运算
同时不要混淆list和numpy区别,list是python提供的可变列表,支持多种元素
而numpy则长度不可变,只支持同类型元素,但同时速度更快,结构更加紧凑,提供了多种操作函数
往往是先将list转化为numpy然后再转为torch
这里设定了numpy每个元素为float32类型,代表所有numpy的所有行的前两个元素形成的列表被转化为torch格式
np_data=np.array(data,dtype='float32')
x_data=torch.form_numpy(np_data[:,0:2])
同时对于目标数据,需要将其排成一列
y_data=torch.from_numpy(np.data[:,-1]).unsqueeze(1)
clamp是一个判断语句,如果y_pred 或者1-y_pred小于这个数值就设置为这个数值
因为log的x区间不能小于等于0
逻辑回归函数调用sigmoid来对矩阵运算的结果进行分类,得到分类概率列表
loss求解损失函数中,会计算出预测值和真实值之间的log,并对输入的x矩阵所有数据的log差求和求平均值mean
ge(0.5)是一个比较器,低于此值归零,高于此值归1,用于分类,返回值与原数据类型相同
(mask==y_data).sum()统计两个torch对象有多少相等的,t这是orch对象的函数,作为神经网络的数据元素,它具备众多函数方法为了神经网络服务
多层神经网络
之前的线性回归模型和逻辑回归模型,因为都涉及到一层w的运算,都被视作单层神经网络
无非是不断优化一层w的值到合适位置而已
事实上,复杂而有效的神经网络是深层的,往往波浪式的w向前传递,同时模拟人脑神经元激活阈值的原理,提出了激活函数
sigmoid
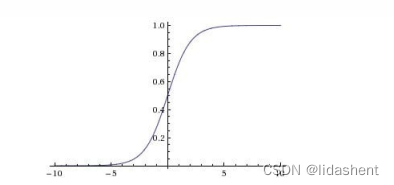
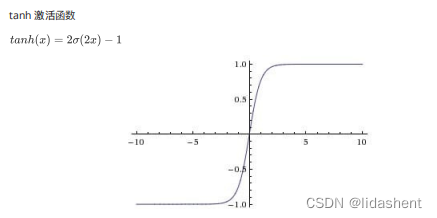
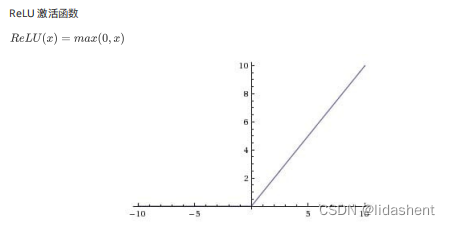
越来越多的实践表明relu的优化效果更好,一层网络是max(0,wx+b),二层就是w2max(0,w1x+b1)+b2
那么为什么需要激活函数呢?
本质上讲激活函数让神经网络有了深层的可能,通过改变w使得网络可以拟合成各种情况
如果不使用激活函数来改变网络形状,那么最后就会变成
w1x w2(w1x) w3(w2(w1x) ) w1w2w3…x Wnx 归根究底还是单层神经网络
多层网络搭建
解决多分类问题
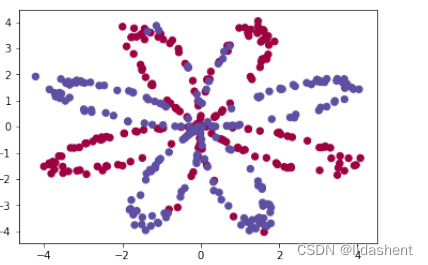
画出分类图形函数::
def plot_decision_boundary(model, x, y):# Set min and max values and give it some paddingx_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1h = 0.01# Generate a grid of points with distance h between themxx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))# Predict the function value for the whole gridZ = model(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)# Plot the contour and training examplesplt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)plt.ylabel('x2')plt.xlabel('x1')plt.scatter(x[:, 0], x[:, 1], c=y.reshape(-1), s=40, cmap=plt.cm.Spectral)
传入模型和数据,即可对数据进行可视化分类
xx,yy=np.meshgrid(np.arange(x_min,x_max,h),np.arange(y_min,y_max,h))
meshgrid传入两个一维数组,生成两个二维数组,xx的shape为(y_max-y_min,x_max-x_min)
yy的shape为(x_max-x_min,y_max-y_min),这个很好理解,可以看做画了一个坐标网格,xx和yy为每一个点都设定了坐标
z=model(np.c_[xx.ravel(),yy.ravel()])
将xx和yy一维展开,然后由np.c_得到它们所标记的每一个点,每个点交给模型,让模型算出新的目标numpy数组,然后让其形状大小和xx相同,这样方便展开绘画

plt.contourf(xx,yy,z,cmap=plt.cm.Spectral)
xx和yy绘制网格,z来画出分割点,cmap来设定颜色,设定为渐变色,从高到低由红绿蓝渐变方便查看
plt.scatter(x[:,0],x[:,1],c=y.reshape(-1),s=40,cmap=plt.cm.Spectral)
根据坐标绘制散点图,参数为x,y坐标,c函数值,散点大小,颜色渐变
那么要分类的图形是怎样的?可以画出一个图
我们要画的是一个复杂的花色图像,红蓝相间,由sin和cos函数组合而成
构思逻辑如下:
指定某个范围的数据生成sin和cos的x坐标值列表
然后根据这些坐标值生成新的坐标y值,即sin,cos值
通过公式[sin(x)*sin(x),sin(x)*cos(x)]来说生成每一组xy的坐标点来进行绘图
然后绘制这些坐标即可
allPoint=400
halfCategory=int(allPoint/2)
xy=np.zeros((allPoint,2))#存储x和y值的坐标矩阵,数据矩阵,400行,2列
y=np.zeros((allPoint,1))#存储y值的坐标矩阵,分类目标矩阵,400行
for i in range(2):#可视化视图ix=range(i*halfCategory,(i+1)*halfCategory)#对xy坐标进行圈定范围t=np.linspace(i*3.12,(i+1)*3.12,halfCategory)#生成sin,cos演化周期的x值x=30*np.sin(8*t)#生成sinx值,用于生成花型图案的基础y矩阵xy[ix]=np.c_[x*np.sin(t),x*np.cos(t)]#构建一个二维矩阵,有两个特殊的一维矩阵构成,将这两个一维矩阵组合生成xy坐标矩阵,放入xy中y[ix]=i#构建坐标值矩阵
plt.scatter(xy[:,0],xy[:,1],c=y.reshape(-1),s=40,cmap=plt.cm.Spectral)
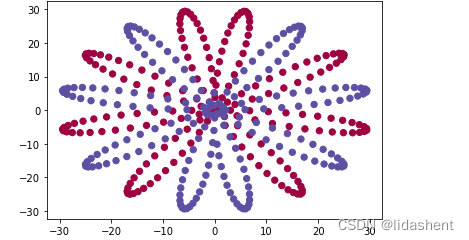
那么红蓝分类的点就当作原始数据,y值目标值当做分类数据,这样xy和y数据矩阵就构建好了
那么接下来我们使用逻辑回归一层分类,二层网络,三层网络分别进行实验分类效果
构建训练参数x,y
初始化wb,设置参数优化器和loss优化器
循环100次优化wb,再次绘图
x_trainData=torch.from_numpy(np.array(xy)).float()
y_trainData=torch.from_numpy(np.array(y)).float()
w=nn.Parameter(torch.randn(2,1))
b=nn.Parameter(torch.randn(1))
def logistic_regression(x):return torch.mm(x,w)+b
optimizer=torch.optim.SGD([w,b],1e-1)
lossor=nn.BCEWithLogitsLoss()
for i in range(100):y_pred=logistic_regression(x_trainData)loss=lossor(y_pred,y_trainData)optimizer.zero_grad()optimizer.step()
将参数进行新绘图
def plot_logistic(x):x = Variable(torch.from_numpy(x).float())out = F.sigmoid(logistic_regression(x))out =out.ge(0.5).float()return out.data.numpy()
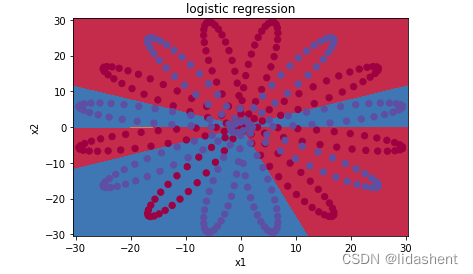
plot_decision_boundary(lambda x_trainData: plot_logistic(x_trainData), x_trainData.data.numpy(), y_trainData.data.numpy())
plt.title('logistic regression')
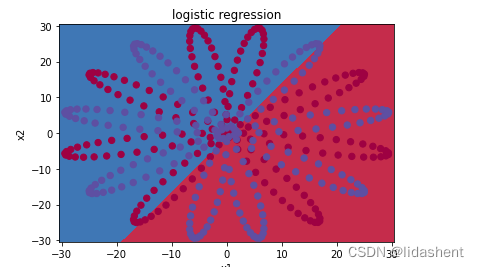
效果并不理想,只能进行简单的二分类
我们构建一个两层图像,并使用tanh作为激活函数,再次看效果
第一层网4个神经元,经过它之后原有的数据被扩容了4倍,如果熟悉矩阵运算,假设原数据为x[100,2],经过w[2,4],就会变成[100,4],然后经过激活函数剪枝,激活部分有用的神经元,最后由一个神经元输出01分类数据
矩阵乘法就是,由mxn的矩阵与nxz的矩阵相乘,得到mxz的新矩阵,其中新矩阵的每一个数值都是由行列坐标ij计算,行对应m的行,列对应z的列,对应值相乘的和为新矩阵的值
比如
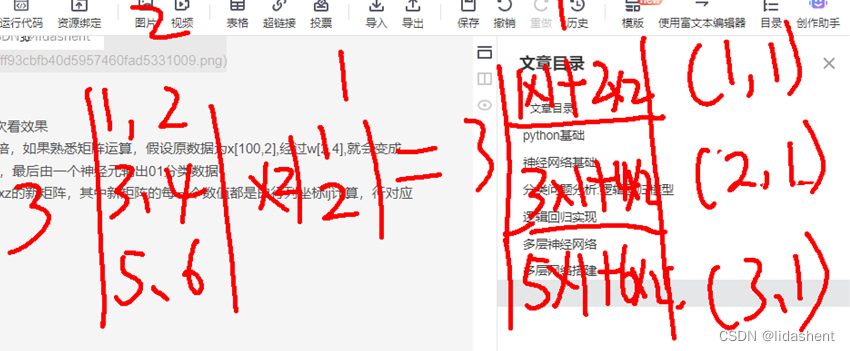
w1=nn.Parameter(torch.randn(2,4))
b1=nn.Parameter(torch.randn(4))
w2=nn.Parameter(torch.randn(4,1))
b2=nn.Parameter(torch.randn(1))
# 定义模型
def two_network(x):x1 = torch.mm(x, w1) + b1x1 = F.tanh(x1) # 使用 PyTorch 自带的 tanh 激活函数x2 = torch.mm(x1, w2) + b2return x2
optimizer=torch.optim.SGD([w1,b1,w2,b2],1.)
for i in range(1000):y_pred=two_network(x_trainData)loss=lossor(y_pred,y_trainData)optimizer.zero_grad()loss.backward()optimizer.step()if i%200==0:print(loss.item())
分类效果并不好,但相比于逻辑回归有了改善
如果想要取得更好的效果,我们可以增加训练神经元的次数和深度,然而需要注意的是神经元的次数优势并不会带来更好的训练效果,因为参数优化有极限的,但是深度结构的改变会带来质的飞跃
我们可以尝试增加多个神经元来模拟分类效果,但是在一些大型项目中这样的神经元可能有几百亿个,逐个设置参数是不合理的,因此提供了参数初始化工具,在设置网络层数的同时将网络结构一并设计,这样我们只需要关注网络的参数和层数如何设计而不用做重复劳动
一个是Sequential,一个是 Module
会得到一个神经网络模型,同时设置了每层神经元的数量和网络结构
seq_net=nn.Sequential(
nn.Linear(2, 10),
nn.Tanh(),
nn.Linear(10, 8),
nn.Tanh(),
nn.Linear(8, 5),
nn.Tanh(),
nn.Linear(5, 1)
)
和单层设计一样,我们可以随意的查看每层的结构和权重参数
seq_net[0]
#Linear(in_features=2, out_features=10, bias=True)
w1=seq_net[0].weight
接下来只需要设置参数优化器,loss优化器,将数据导入seq_net就能够执行训练了,lossor之前已经进行过定义,就是nn.BCEWithlogitsloss()
param=seq_net.parameters()
paramOptimizer=torch.optim.SGD(param,1.)
for i in range(20000):y_pred=seq_net(x_trainData)loss=lossor(y_pred,y_trainData)paramOptimizer.zero_grad()loss.backward()paramOptimizer.step()
查看多层网络的分类效果
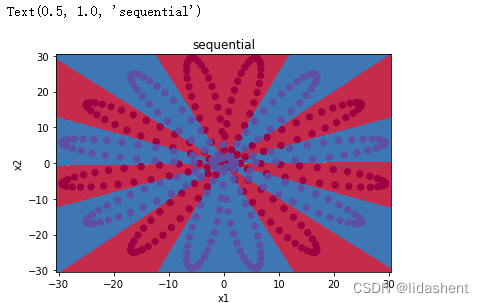
当然对于网络结构还有更好的写法,使用modul定义模型更符合语法规范
模板为:
可以设计网络结构,然后设置前向传播如何构建,就像一个类调用
Module 里面也可以使用 Sequential
class 网络名字(nn.Module):def __init__(self, 一些定义的参数):super(网络名字, self).__init__()self.layer1 = nn.Linear(num_input, num_hidden)self.layer2 = nn.Sequential(...)...定义需要用的网络层def forward(self, x): # 定义前向传播x1 = self.layer1(x)x2 = self.layer2(x)x = x1 + x2...return x
如下设计一个三层网络,查看权重和网络层结构就像类调用一样
class modelNet(nn.Module):def __init__(self,inputLayer,hiddenLayer,outputLayer):super(modelNet,self).__init__()self.layer1=nn.Linear(inputLayer,hiddenLayer)self.layer2=nn.Tanh()self.layer3=nn.Linear(hiddenLayer,outputLayer)def forward(self,x):x=self.layer1(x)x=self.layer2(x)x=self.layer3(x)return x
mNet=modelNet(2,4,1)
mNet.layer1.weight
对其进行训练
mParamOptimizer=torch.optim.SGD(mNet.parameters(),1.)
for i in range(20000):y_pred=mNet(x_trainData)loss=lossor(y_pred,y)mParamOptimizer.zero_grad()loss.backward()mParamOptimizer.step()
保存模型
1,将网络结构和参数一起保存
前面是网络模型,后面是路径
torch.save(seq_net, 'save_seq_net.pth')
读取模型和参数,得到新的神经网络对象
seq_net1 = torch.load('save_seq_net.pth')
2,只保存参数
# 保存模型参数
torch.save(seq_net.state_dict(), 'save_seq_net_params.pth')
已经有网络结构了,只需要加载预设参数
得到新的神经网络
seq_net2.load_state_dict(torch.load('save_seq_net_params.pth'))
相关文章:

pytorch_神经网络构建1
文章目录 pytorch简介神经网络基础分类问题分析:逻辑回归模型逻辑回归实现多层神经网络多层网络搭建保存模型 pytorch简介 为什么神经网络要自定义数据类型torch.tensor? tensor可以放在gpu上训练,支持自动求导,方便快速训练,同时支持numpy的运算,是加强版,numpy不支持这些 为…...
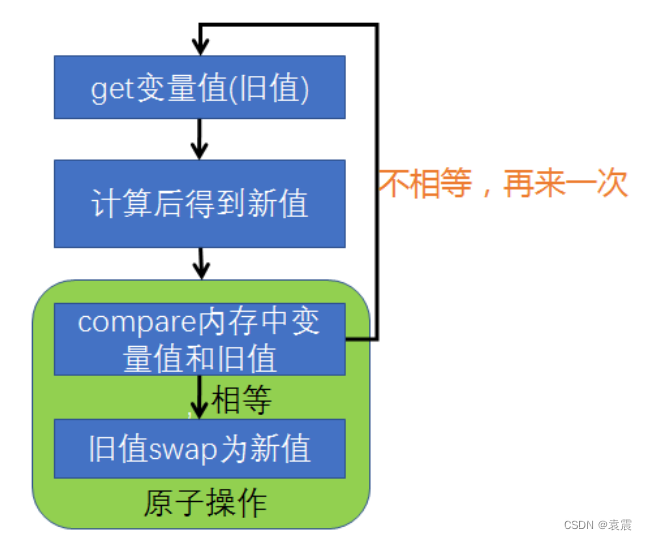
Android 多线程并发详解
一,基础概念 1.1什么是CPU 中央处理器(CPU),是电子计算机的主要设备之一,电脑中的核心配件。其功能主要是解释计算机指令以及处理计算机软件中的数据。CPU是计算机中负责读取指令,对指令译码并执行指令的…...

系统架构设计:8 论软件架构风格
目录 一 软件架构风格 1 数据流风格 (1)批处理风格 (2)管道-过滤器风格...
 - 短语匹配以及slop参数)
[Elasticsearch] 邻近匹配 (一) - 短语匹配以及slop参数
本文翻译自Elasticsearch官方指南的Proximity Matching一章。 邻近匹配(Proximity Matching) 使用了TF/IDF的标准全文搜索将文档,或者至少文档中的每个字段,视作"一大袋的单词"(Big bag of Words)。match查询能够告诉我们这个袋子中是否包含了…...

Bootstrap中让元素尽可能往父容器的左侧靠近或右侧造近(左浮动和右浮动)
在Bootstrap中,float-left是一个用于浮动元素的CSS类。它的作用是将一个元素向左浮动,使其在父容器内尽可能靠近左侧边缘,同时允许其他元素在其右侧排列。 使用float-left类可以创建多列布局,将元素水平排列在一行上,…...
网络流量安全分析-工作组异常
在网络中,工作组异常分析具有重要意义。以下是网络中工作组异常分析的几个关键点: 检测网络攻击:网络中的工作组异常可能是由恶意活动引起的,如网络攻击、病毒感染、黑客入侵等。通过对工作组异常的监控和分析,可以快…...
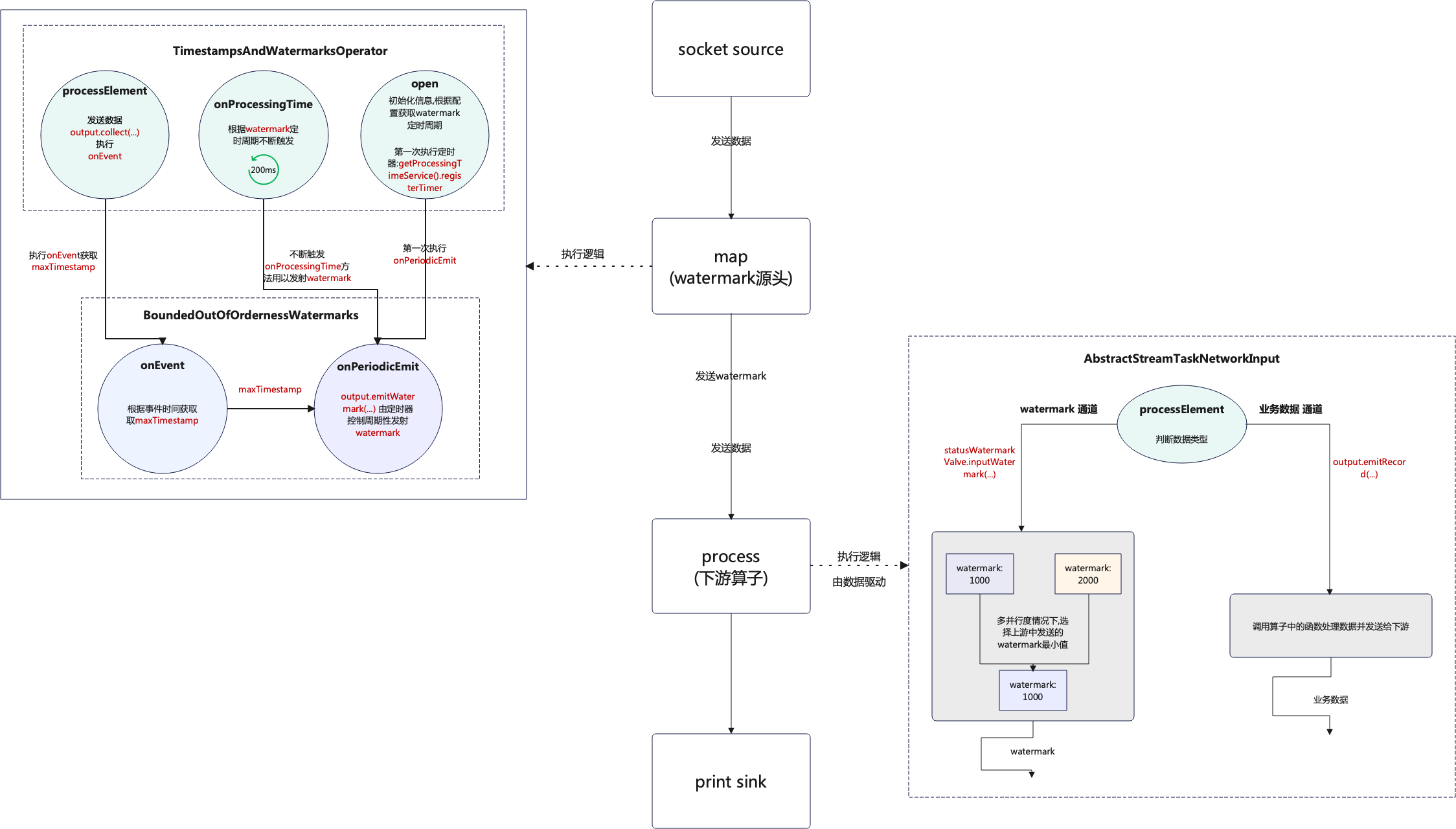
Flink之Watermark源码解析
1. WaterMark源码分析 在Flink官网中介绍watermark和数据是异步处理的,通过分析源码得知这个说法不够准确或者说不够详细,这个异步处理要分为两种情况: watermark源头watermark下游 这两种情况的处理方式并不相同,在watermark的源头确实是异步处理的,但是在下游只是做的判断,这…...
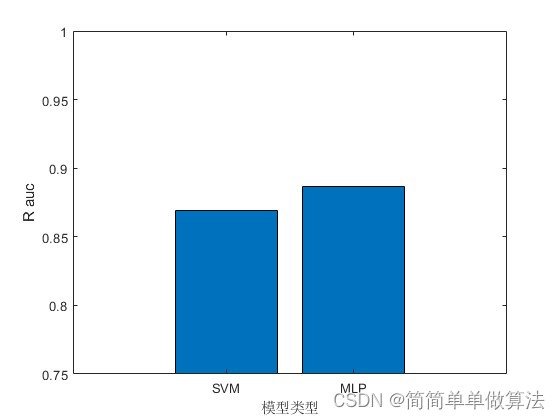
基于支持向量机SVM和MLP多层感知神经网络的数据预测matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 一、支持向量机(SVM) 二、多层感知器(MLP) 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 .…...

【微服务】RedisSearch 使用详解
目录 一、RedisJson介绍 1.1 RedisJson是什么 1.2 RedisJson特点 1.3 RedisJson使用场景 1.3.1 数据结构化存储 1.3.2 实时数据分析 1.3.3 事件存储和分析 1.3.4 文档存储和检索 二、当前使用中的问题 2.1 刚性数据库模式限制了敏捷性 2.2 基于磁盘的文档存储导致瓶…...
第三章 栈、队列和数组
第三章 栈、队列、数组 栈栈的基本概念栈的顺序实现栈的链接实现栈的简单应用和递归 队列队列的基本概念队列的顺序实现队列的链接实现 数组数组的逻辑结构和基本运算数组的存储结构矩阵的压缩存储 小试牛刀 栈和队列可以看作是特殊的线性表,是运算受限的线性表 栈 …...
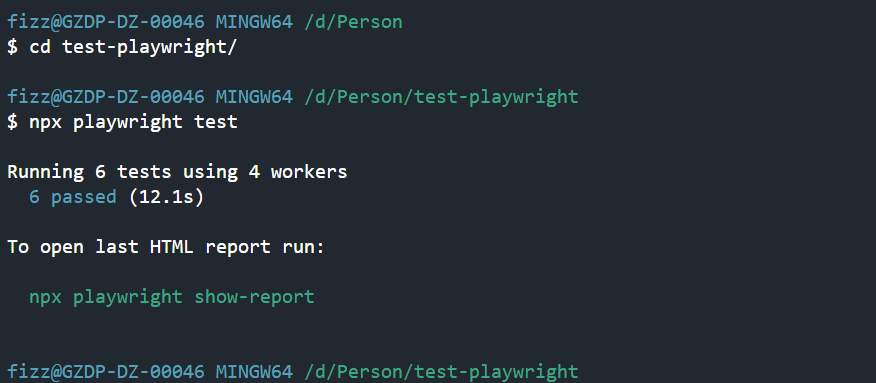
使用GitLab CI/CD 定时运行Playwright自动化测试用例
创建项目并上传到GitLab npm init playwright@latest test-playwright # 一路enter cd test-playwright # 运行测试用例 npx playwright test常用指令 # Runs the end-to-end tests. npx playwright test# Starts the interactive UI mode. npx playwright...

Suricata + Wireshark离线流量日志分析
目录 一、访问一个404网址,触发监控规则 1、使用python搭建一个虚拟访问网址 2、打开Wireshark,抓取流量监控 3、在Suricata分析数据包 流量分析经典题型 入门题型 题目:Cephalopod(图片提取) 进阶题型 题目:抓到一只苍蝇(数据包筛选…...

JMeter基础 —— 使用Badboy录制JMeter脚本!
1、使用Badboy录制JMeter脚本 打开Badboy工具开始进行脚本录制: (1)当我们打开Badboy工具时,默认就进入录制状态。 如下图: 当然我们也可以点击录制按钮进行切换。 (2)在地址栏中输入被测地…...
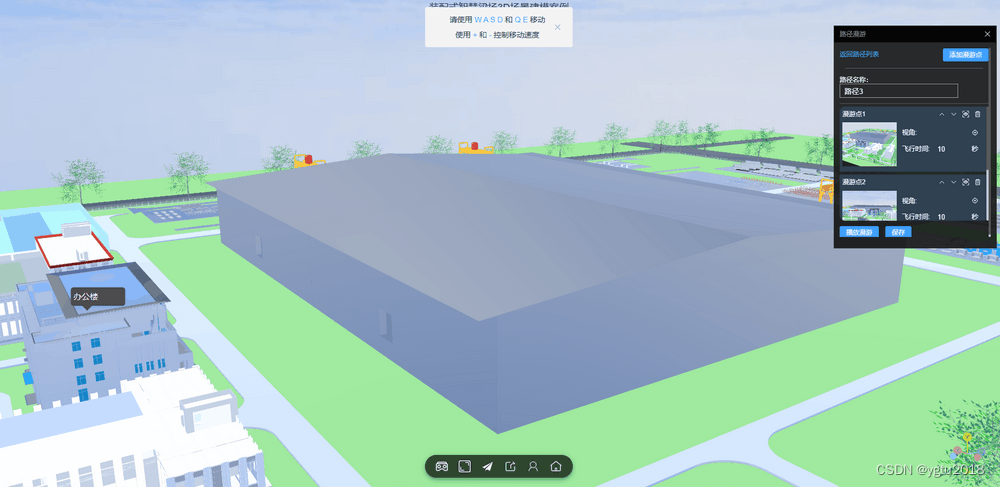
3D孪生场景搭建:3D漫游
上一篇 文章介绍了如何使用 NSDT 编辑器 制作模拟仿真应用场景,今天这篇文章将介绍如何使用NSDT 编辑器 设置3D漫游。 1、什么是3D漫游 3D漫游是指基于3D技术,将用户带入一个虚拟的三维环境中,通过交互式的手段,让用户可以自由地…...

三、综合——计算机应用基础
文章目录 一、计算机概述二、计算机系统的组成三、计算机中数据的表示四、数据库系统五、多媒体技术5.1 多媒体的基本概念5.2 多媒体计算机系统组成5.3 多媒体关键硬件一、计算机概述 1854 年,英国数学家布尔(George Boo1e,1824-1898 年)提出了符号逻辑的思想,数十年后形成了…...
【Redis】SpringBoot整合redis
文章目录 一、SpringBoot整合二、RedisAutoConfiguration自动配置类1、整合测试一下 三、自定义RedisTemplete1、在测试test中使用自定义的RedisTemplete2、自定义RedisTemplete后测试 四、在企业开发中,大部分情况下都不会使用原生方式编写redis1、编写RedisUtils代…...
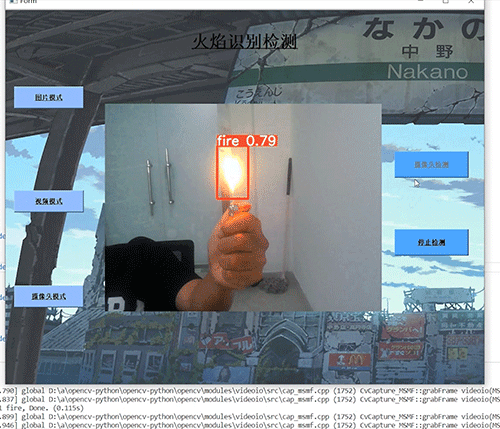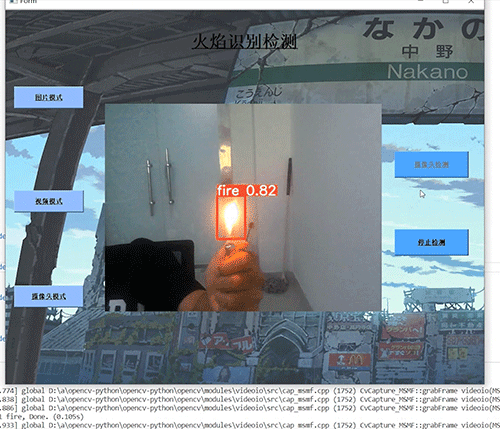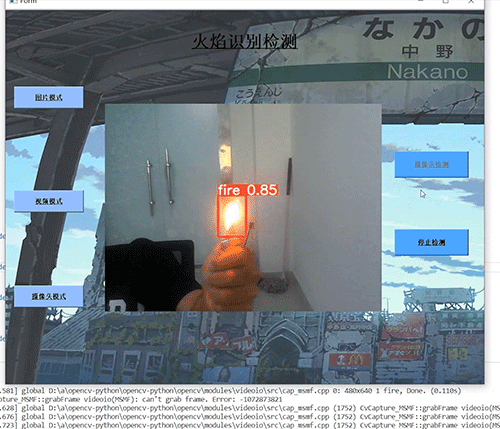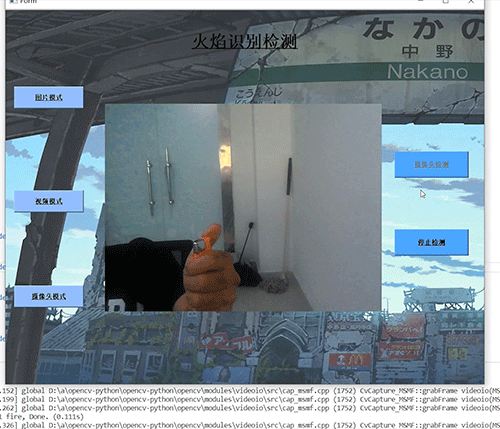
竞赛选题 深度学习 python opencv 火焰检测识别 火灾检测
文章目录 0 前言1 基于YOLO的火焰检测与识别2 课题背景3 卷积神经网络3.1 卷积层3.2 池化层3.3 激活函数:3.4 全连接层3.5 使用tensorflow中keras模块实现卷积神经网络 4 YOLOV54.1 网络架构图4.2 输入端4.3 基准网络4.4 Neck网络4.5 Head输出层 5 数据集准备5.1 数…...

Python Parser 因子计算性能简单测试
一直以来,Python 都在量化金融领域扮演着至关重要的角色。得益于 Python 强大的库和工具,用户在处理金融数据、进行数学建模和机器学习时变得更加便捷。但作为一种解释性语言,相对较慢的执行速度也限制了 Python 在一些需要即时响应的场景中的…...
【java学习】特殊流程控制语句(8)
文章目录 1. break语句2. continue语句3. return语句4. 特殊流程语句控制说明 1. break语句 break语句用于终止某个语句块的执行,终止当前所在循环。 语法结构: { ...... break; ...... } 例子如下: (1&…...

pyinstaller 使用
python 打包不依赖于系统环境的应用总结 【pyd库和pyinstaller可执行程序的区别: 在实际开发中,对于多人协作的大型项目, 或者是基于支持Python的商业软件的二次开发等, 如果将py脚本打包成exe可执行文件,不仅不方便调用ÿ…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

ArcGIS Pro+ArcGIS给你的地图加上北回归线!
今天来看ArcGIS Pro和ArcGIS中如何给制作的中国地图或者其他大范围地图加上北回归线。 我们将在ArcGIS Pro和ArcGIS中一同介绍。 1 ArcGIS Pro中设置北回归线 1、在ArcGIS Pro中初步设置好经纬格网等,设置经线、纬线都以10间隔显示。 2、需要插入背会归线…...
