23.2.23 22湖北省赛 B
好久没打卡了, 随便找的个水题写
这题是简单难度的
a=b=1
所以可以找到固定规律, 通过手动模拟可以发现
假设两种水叫做a水和b水
先倒入a水 1:0 倒入b水 1:1
此时水杯为
倒出一半的混合物, 因为ab水互溶, 比例不变
再加入a水或者b水将容器填满 比例现在变为 3:1
混合之后再加入a水或者b水 比例变为3:5 或者7:1
这样推下去我们可以发现一个规律
符合题目条件的有:
1:1 3:1 7:1 3:5.......
可以发现, 比值加起来是2的次幂
以2的次幂为规律判断是否符合题目条件即可
注意, 样例中的2:6实质上约分后为1:3 , 需要对数据进行约分
/*
⣿⣿⣿⣿⣿⣿⡷⣯⢿⣿⣷⣻⢯⣿⡽⣻⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣇⠸⣿⣿⣆⠹⣿⣿⢾⣟⣯⣿⣿⣿⣿⣿⣿⣽⣻⣿⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣻⣽⡿⣿⣎⠙⣿⣞⣷⡌⢻⣟⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣿⣿⣿⣿⣿⣿⡄⠹⣿⣿⡆⠻⣿⣟⣯⡿⣽⡿⣿⣿⣿⣿⣽⡷⣯⣿⣿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣟⣷⣿⣿⣿⡀⠹⣟⣾⣟⣆⠹⣯⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⢠⡘⣿⣿⡄⠉⢿⣿⣽⡷⣿⣻⣿⣿⣿⣿⡝⣷⣯⢿⣿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣯⢿⣾⢿⣿⡄⢄⠘⢿⣞⡿⣧⡈⢷⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⢸⣧⠘⣿⣷⠈⣦⠙⢿⣽⣷⣻⣽⣿⣿⣿⣿⣌⢿⣯⢿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⣟⣯⣿⢿⣿⡆⢸⡷⡈⢻⡽⣷⡷⡄⠻⣽⣿⣿⡿⣿⣿⣿⣿⣿⣿⣷⣿⣿⣿⣿⣏⢰⣯⢷⠈⣿⡆⢹⢷⡌⠻⡾⢋⣱⣯⣿⣿⣿⣿⡆⢻⡿⣿⣿⣿
⣿⣿⣿⣿⣿⣿⡎⣿⢾⡿⣿⡆⢸⣽⢻⣄⠹⣷⣟⣿⣄⠹⣟⣿⣿⣟⣿⣿⣿⣿⣿⣿⣽⣿⣿⣿⡇⢸⣯⣟⣧⠘⣷⠈⡯⠛⢀⡐⢾⣟⣷⣻⣿⣿⣿⡿⡌⢿⣻⣿⣿
⣿⣿⣿⣿⣿⣿⣧⢸⡿⣟⣿⡇⢸⣯⣟⣮⢧⡈⢿⣞⡿⣦⠘⠏⣹⣿⣽⢿⣿⣿⣿⣿⣯⣿⣿⣿⡇⢸⣿⣿⣾⡆⠹⢀⣠⣾⣟⣷⡈⢿⣞⣯⢿⣿⣿⣿⢷⠘⣯⣿⣿
⣿⣿⣿⣿⣿⣿⣿⡈⣿⢿⣽⡇⠘⠛⠛⠛⠓⠓⠈⠛⠛⠟⠇⢀⢿⣻⣿⣯⢿⣿⣿⣿⣷⢿⣿⣿⠁⣾⣿⣿⣿⣧⡄⠇⣹⣿⣾⣯⣿⡄⠻⣽⣯⢿⣻⣿⣿⡇⢹⣾⣿
⣿⣿⣿⣿⣿⣿⣿⡇⢹⣿⡽⡇⢸⣿⣿⣿⣿⣿⣞⣆⠰⣶⣶⡄⢀⢻⡿⣯⣿⡽⣿⣿⣿⢯⣟⡿⢀⣿⣿⣿⣿⣿⣧⠐⣸⣿⣿⣷⣿⣿⣆⠹⣯⣿⣻⣿⣿⣿⢀⣿⢿
⣿⣿⣿⣿⣿⣿⣿⣿⠘⣯⡿⡇⢸⣿⣿⣿⣿⣿⣿⣿⣧⡈⢿⣳⠘⡄⠻⣿⢾⣽⣟⡿⣿⢯⣿⡇⢸⣿⣿⣿⣿⣿⣿⡀⢾⣿⣿⣿⣿⣿⣿⣆⠹⣾⣷⣻⣿⡿⡇⢸⣿
⣿⣿⣿⣿⣿⣿⣿⣿⡇⢹⣿⠇⢸⣿⣿⣿⣿⣿⣿⣿⣿⣷⣄⠻⡇⢹⣆⠹⣟⣾⣽⣻⣟⣿⣽⠁⣾⣿⣿⣿⣿⣿⣿⣇⣿⣿⠿⠛⠛⠉⠙⠋⢀⠁⢘⣯⣿⣿⣧⠘⣿
⣿⣿⣿⣿⣿⣿⣿⣿⣿⡈⣿⡃⢼⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣦⡙⠌⣿⣆⠘⣿⣞⡿⣞⡿⡞⢠⣿⣿⣿⣿⣿⡿⠛⠉⠁⢀⣀⣠⣤⣤⣶⣶⣶⡆⢻⣽⣞⡿⣷⠈⣿
⣿⣿⣿⣿⣿⣿⣿⣿⡿⠃⠘⠁⠉⠉⠉⠉⠉⠉⠉⠉⠉⠙⠛⠛⢿⣄⢻⣿⣧⠘⢯⣟⡿⣽⠁⣾⣿⣿⣿⣿⣿⡃⢀⢀⠘⠛⠿⢿⣻⣟⣯⣽⣻⣵⡀⢿⣯⣟⣿⢀⣿
⣿⣿⣿⣟⣿⣿⣿⣿⣶⣶⡆⢀⣿⣾⣿⣾⣷⣿⣶⠿⠚⠉⢀⢀⣤⣿⣷⣿⣿⣷⡈⢿⣻⢃⣼⣿⣿⣿⣿⣻⣿⣿⣿⡶⣦⣤⣄⣀⡀⠉⠛⠛⠷⣯⣳⠈⣾⡽⣾⢀⣿
⣿⢿⣿⣿⣻⣿⣿⣿⣿⣿⡿⠐⣿⣿⣿⣿⠿⠋⠁⢀⢀⣤⣾⣿⣿⣿⣿⣿⣿⣿⣿⣌⣥⣾⡿⣿⣿⣷⣿⣿⢿⣷⣿⣿⣟⣾⣽⣳⢯⣟⣶⣦⣤⡾⣟⣦⠘⣿⢾⡁⢺
⣿⣻⣿⣿⡷⣿⣿⣿⣿⣿⡗⣦⠸⡿⠋⠁⢀⢀⣠⣴⢿⣿⣽⣻⢽⣾⣟⣷⣿⣟⣿⣿⣿⣳⠿⣵⣧⣼⣿⣿⣿⣿⣿⣾⣿⣿⣿⣿⣿⣽⣳⣯⣿⣿⣿⣽⢀⢷⣻⠄⠘
⣿⢷⣻⣿⣿⣷⣻⣿⣿⣿⡷⠛⣁⢀⣀⣤⣶⣿⣛⡿⣿⣮⣽⡻⣿⣮⣽⣻⢯⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣯⢀⢸⣿⢀⡆
⠸⣟⣯⣿⣿⣷⢿⣽⣿⣿⣷⣿⣷⣆⠹⣿⣶⣯⠿⣿⣶⣟⣻⢿⣷⣽⣻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⢀⣯⣟⢀⡇
⣇⠹⣟⣾⣻⣿⣿⢾⡽⣿⣿⣿⣿⣿⣆⢹⣶⣿⣻⣷⣯⣟⣿⣿⣽⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⢀⡿⡇⢸⡇
⣿⣆⠹⣷⡻⣽⣿⣯⢿⣽⣻⣿⣿⣿⣿⣆⢻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠛⢻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠇⢸⣿⠇⣼⡇
⡙⠾⣆⠹⣿⣦⠛⣿⢯⣷⢿⡽⣿⣿⣿⣿⣆⠻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠃⠎⢸⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠏⢀⣿⣾⣣⡿⡇
⣿⣷⡌⢦⠙⣿⣿⣌⠻⣽⢯⣿⣽⣻⣿⣿⣿⣧⠩⢻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡏⢰⢣⠘⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⠃⢀⢀⢿⣞⣷⢿⡇
⣿⣽⣆⠹⣧⠘⣿⣿⡷⣌⠙⢷⣯⡷⣟⣿⣿⣿⣷⡀⡹⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣷⣈⠃⣸⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠟⢀⣴⡧⢀⠸⣿⡽⣿⢀
⢻⣽⣿⡄⢻⣷⡈⢿⣿⣿⢧⢀⠙⢿⣻⡾⣽⣻⣿⣿⣄⠌⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠛⢁⣰⣾⣟⡿⢀⡄⢿⣟⣿⢀
⡄⢿⣿⣷⢀⠹⣟⣆⠻⣿⣿⣆⢀⣀⠉⠻⣿⡽⣯⣿⣿⣷⣈⢻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⠋⢀⣠⠘⣯⣷⣿⡟⢀⢆⠸⣿⡟⢸
⣷⡈⢿⣿⣇⢱⡘⢿⣷⣬⣙⠿⣧⠘⣆⢀⠈⠻⣷⣟⣾⢿⣿⣆⠹⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡿⠋⣠⡞⢡⣿⢀⣿⣿⣿⠇⡄⢸⡄⢻⡇⣼
⣿⣷⡈⢿⣿⡆⢣⡀⠙⢾⣟⣿⣿⣷⡈⠂⠘⣦⡈⠿⣯⣿⢾⣿⣆⠙⠻⠿⠿⠿⠿⡿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠿⠛⢋⣠⣾⡟⢠⣿⣿⢀⣿⣿⡟⢠⣿⢈⣧⠘⢠⣿
⣿⣿⣿⣄⠻⣿⡄⢳⡄⢆⡙⠾⣽⣿⣿⣆⡀⢹⡷⣄⠙⢿⣿⡾⣿⣆⢀⡀⢀⢀⢀⢀⢀⢀⢀⢀⢀⢀⢀⢀⣀⣠⣴⡿⣯⠏⣠⣿⣿⡏⢸⣿⡿⢁⣿⣿⢀⣿⠆⢸⣿
⣿⣿⣿⣿⣦⡙⣿⣆⢻⡌⢿⣶⢤⣉⣙⣿⣷⡀⠙⠽⠷⠄⠹⣿⣟⣿⣆⢙⣋⣤⣤⣤⣄⣀⢀⢀⢀⢀⣾⣿⣟⡷⣯⡿⢃⣼⣿⣿⣿⠇⣼⡟⣡⣿⣿⣿⢀⡿⢠⠈⣿
⣿⣿⣿⣿⣿⣷⣮⣿⣿⣿⡌⠁⢤⣤⣤⣤⣬⣭⣴⣶⣶⣶⣆⠈⢻⣿⣿⣆⢻⣿⣿⣿⣿⣿⣿⣷⣶⣤⣌⣉⡘⠛⠻⠶⣿⣿⣿⣿⡟⣰⣫⣴⣿⣿⣿⣿⠄⣷⣿⣿⣿
*/
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <queue>
#include <cmath>
#include <cstring>
#include <string>
#include <stack>
#include <deque>
#include <map>
#include <set>
#include <bitset>
#include <unordered_map>
#include <unordered_set>
using namespace std;
#define ll long long
#define endl "\n"
#define R cin>>
#define S second
#define F first
#define ln cout<<endl;
#define rep(i, a, b) for (ll i = (a); i <= (b); i++)
#define repr(i, a, b) for (ll i = (a); i < (b); i++)
#define rrep(i, a, b) for (ll i = (b); i >= (a); i--)
#define rrepr(i, a, b) for (ll i = (b); i > (a); i--)
#define mem(a) memset((a),0,sizeof (a));
#define min(a,b) ((a)<(b)?(a):(b))
#define max(a,b) ((a)>(b)?(a):(b))
#define yes cout<<"YES"<<endl;
#define no cout<<"NO"<<endl;
#define debug cout<<"here!"<<endl;ll cnt,n,m,t,ans,ant;
const int N=1e5+10;
const int INF=0x3f3f3f3f;
const ll llINF=0x3f3f3f3f3f3f3f3f;
ll arr[N];
string str;inline ll read()
{char c = getchar();int x = 0,s = 1;while(c < '0' || c > '9') {if(c == '-') s = -1;c = getchar();}//是符号while(c >= '0' && c <= '9') {x = x*10 + c -'0';c = getchar();}//是数字return x*s;
}void solve()
{R n>>m>>cnt>>cnt;cnt=__gcd(n,m);n/=cnt;m/=cnt;ans=n+m;rep(i,1,63)if(ans==arr[i]) {cout<<i+1<<endl;return;} cout<<-1<<endl;return;
}int main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);//所有输入用cin//所有输出用coutarr[1]=2;rep(i,2,63) arr[i]=arr[i-1]*2;cin>>t;while(t--)solve();return 0;
}相关文章:

23.2.23 22湖北省赛 B
好久没打卡了, 随便找的个水题写 这题是简单难度的 ab1 所以可以找到固定规律, 通过手动模拟可以发现 假设两种水叫做a水和b水 先倒入a水 1:0 倒入b水 1:1 此时水杯为 倒出一半的混合物, 因为ab水互溶, 比例不变 再加入a水或者b水将容器填满 比例现在变为 3:1 混合之后再…...
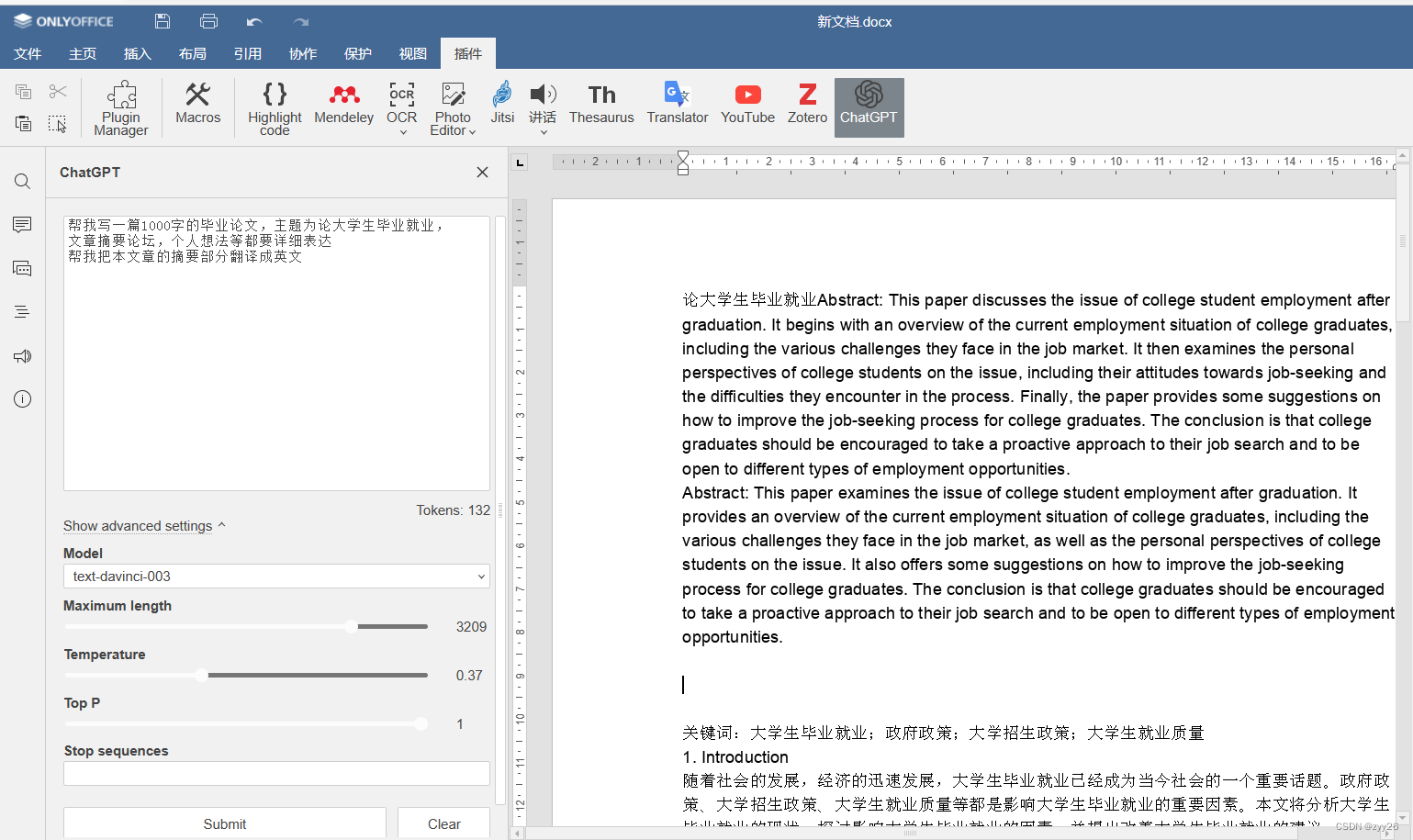
ONLYOFFICE中的chatGPT 是如何编写毕业论文以及翻译多种语言的
前言 chatGPT这款软件曾被多个国家的大学禁用,我们也多次在网上看到chatGPT帮助应届毕业生编写毕业答辩论文,但是这款软件目前还没有在国内正式上线,ONLYOFFICE7.3版本更新后呢,就添加了chatGPT该功能,并且正常使用。 …...
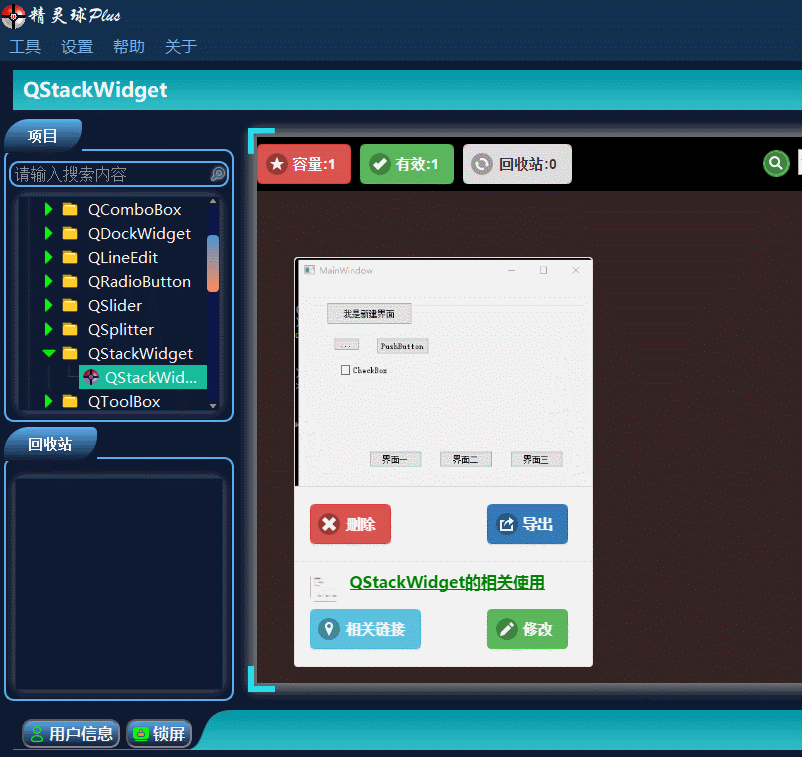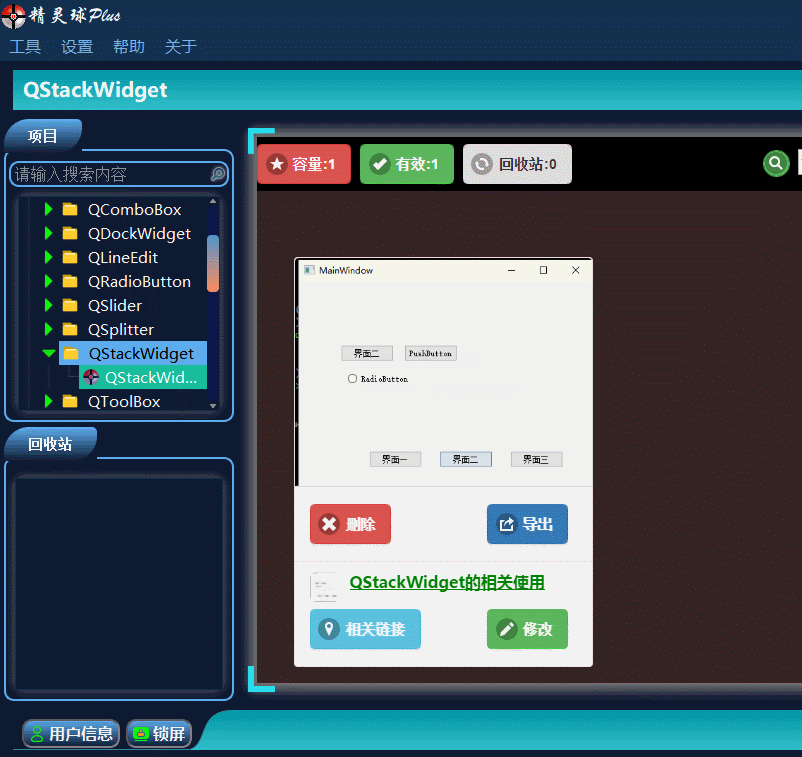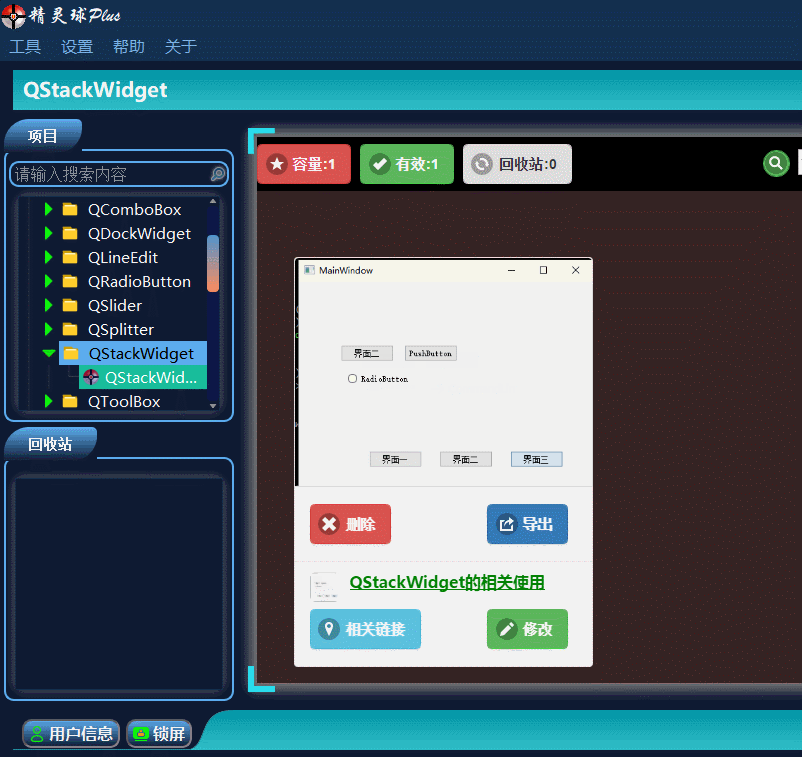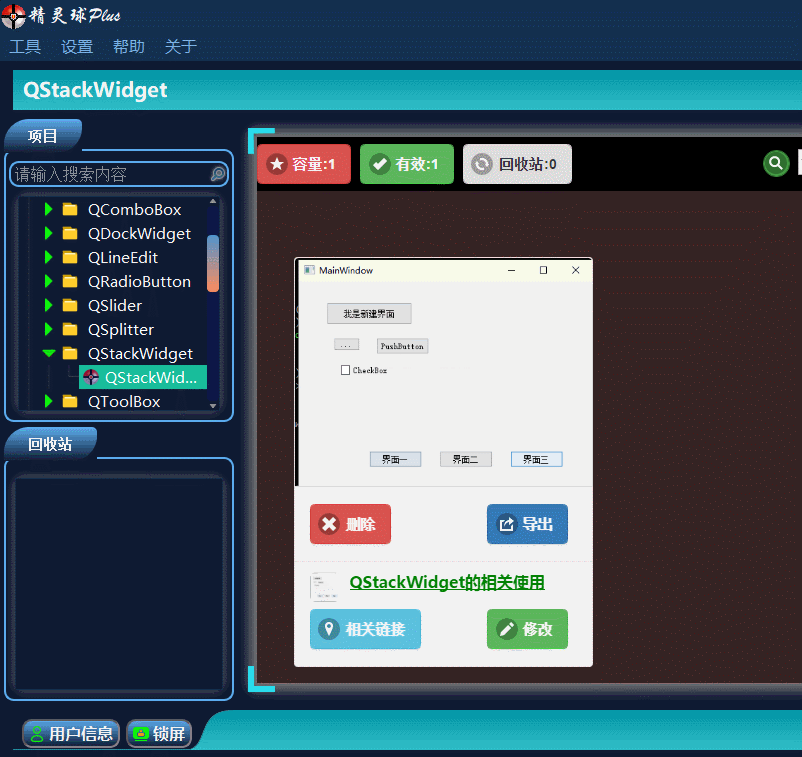
QT入门Containers之QStackedWidget
目录 一、QStackedWidget界面相关 1、布局介绍 2、插入界面 3、插入类界面 二、Demo展示 此文为作者原创,创作不易,转载请标明出处! 一、QStackedWidget界面相关 1、布局介绍 QStackedWidget这个控件在界面布局时,使用还…...

Java学习-IO流-字节缓冲流
Java学习-IO流-字节缓冲流 IO流体系↙ ↘字节流 字符流↙ ↘ ↙ ↘InputStream OutputStream Reader Writer↓ ↓ ↓ ↓ FileInputStream FileOutputStream FileRe…...

C++这么难,为什么我们还要学习C++?
前言 C 可算是一种声名在外的编程语言了。这个名声有好有坏,从好的方面讲,C 性能非常好,哪个编程语言性能好的话,总忍不住要跟 C 来单挑一下;从坏的方面讲,它是臭名昭著的复杂、难学、难用。当然ÿ…...
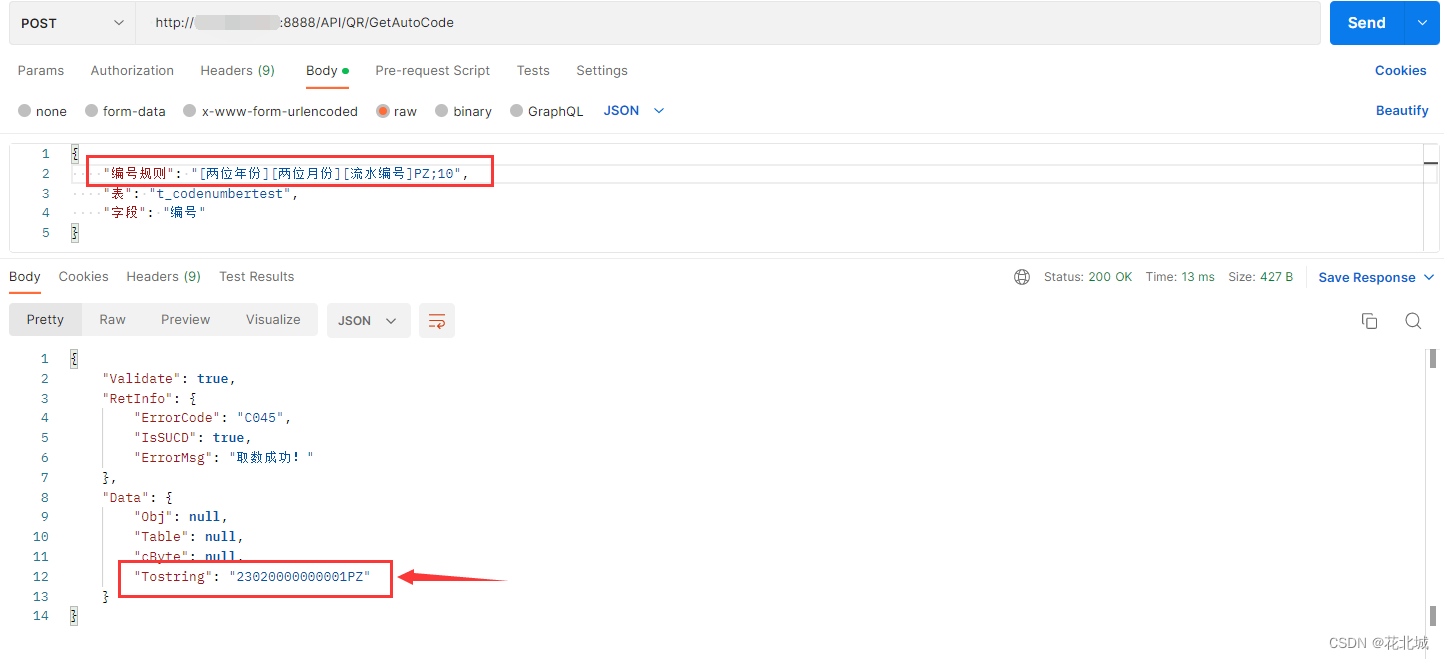
C#底层库--业务单据号生成器(定义规则、自动编号、流水号)
系列文章 C#底层库–MySQL数据库访问操作辅助类(推荐阅读) 本文链接:https://blog.csdn.net/youcheng_ge/article/details/126886379 C#底层库–JSON帮助类_详细(序列化、反序列化、list、datatable) 本文链接&…...
)
vue3项目练习大全(附github源码)
vue慢慢的成为了前端最受欢迎的框架之一,在很多项目之中开发都能用得到,如今也已经发展到3.0了,可能是因为这个框架可以提高工作效率,因此受到大家的追捧,在之前的文章里面也说过,2019年,大前端…...
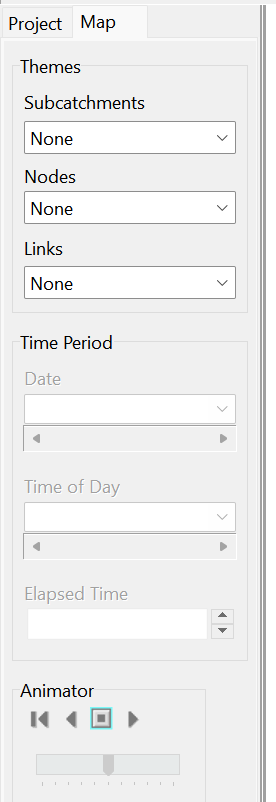
SWMM从入门到实践教程 01 SWMM软件介绍
文章目录1 软件介绍2 软件面板2.1 主菜单2.1.1文件菜单(File)2.1.2 编辑菜单(Edit)2.1.3 视图菜单(View)2.1.4 工程菜单(Project)2.1.5 报告菜单(Report)2.1.…...
)
CSS中的text-overflow属性详解 (控制文字在一行显示,超出部分加省略号)
text-overflow: ellipsis; 表示当文本内容超出所在容器的宽度时,用省略号来代替超出的部分。white-space:nowrap; 表示文本不换行。overflow: hidden; 表示超出容器的内容将被隐藏。 将这三个加入需要控制的css的属性中,就能控制文字在一行显示ÿ…...

基于pytorch实现模型剪枝
一,剪枝分类二,PyTorch 的剪枝三,总结参考资料一,剪枝分类 所谓模型剪枝,其实是一种从神经网络中移除"不必要"权重或偏差(weigths/bias)的模型压缩技术。关于什么参数才是“不必要的”,这是一个目前依然在研究的领域。 1.1,非结构化剪枝 非结构化剪枝(U…...

写出高质量的前端代码之消除代码中的重复
软件开发中,有个很重要的DRY原则,即Dont Repeat Yourself,也就是不要重复自己。 重复的代码会带来以下问题: 开发效率低,重复造轮子不同人开发的同一类功能,质量层次不齐修改问题时可能会遗漏,…...
怎么从零开始学黑客,黑客零基础怎么自学
很多朋友对成为黑客很感兴趣,很大原因是因为看到电影中黑客的情节觉的特别的酷,看到他们动动手指就能进入任何系统,还有很多走上黑客之路的朋友仅仅是因为自己的qq被盗了,或者游戏里的装备被别人偷了,想要自己盗回来&a…...
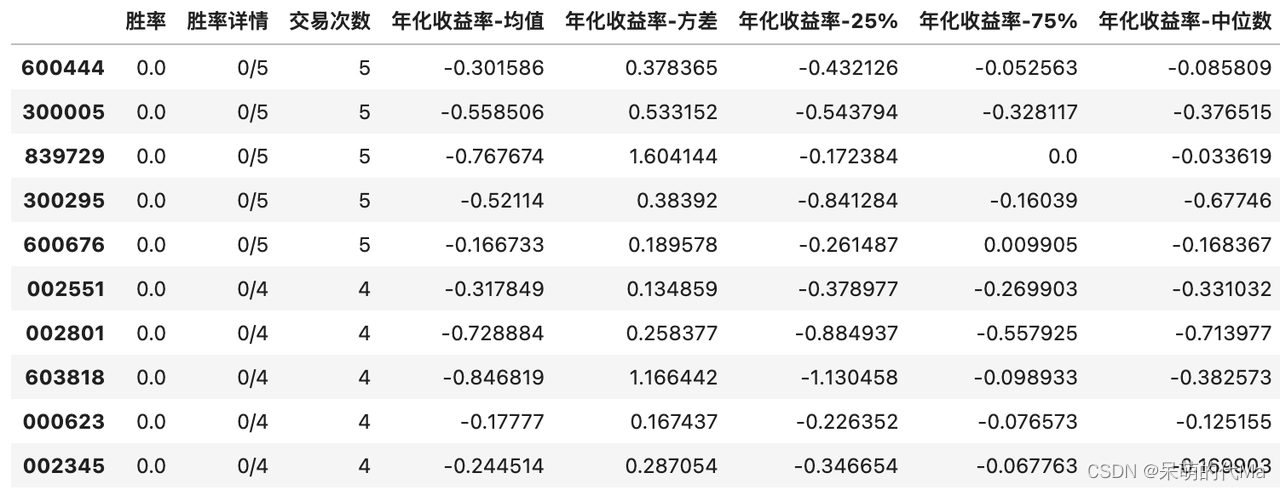
量化择时——资金流择时策略(第1部分—因子测算)
文章目录资金流模型概述资金流模型的有效性逻辑资金流向指标MFI(Money Flow Index)MFI指标测算测算规则测算结论资金流模型概述 通常,资金流是一种反映股票供给信息的指标,宏观上来讲,我们知道一个道理:僧…...

Openwrt中动态IPV6 防火墙的正确设置方法
环境:光猫桥接公网IPV6 问题:动态IPV6地址不知道怎么设置防火墙 解决办法:模糊匹配前缀,特定后缀 背景:将家中光猫桥接后,获得了公网的IPV6地址,可以从外部用IPV6访问家中的设备,但I…...

JS的基本数据类型和引用数据类型
ES6 引入了一种新的原始数据类型 Symbol,表示独一无二的值。它是 JavaScript 语言的第七种数据类型,前六种是:Undefined、Null、布尔值(Boolean)、字符串(String)、数值(Number&…...
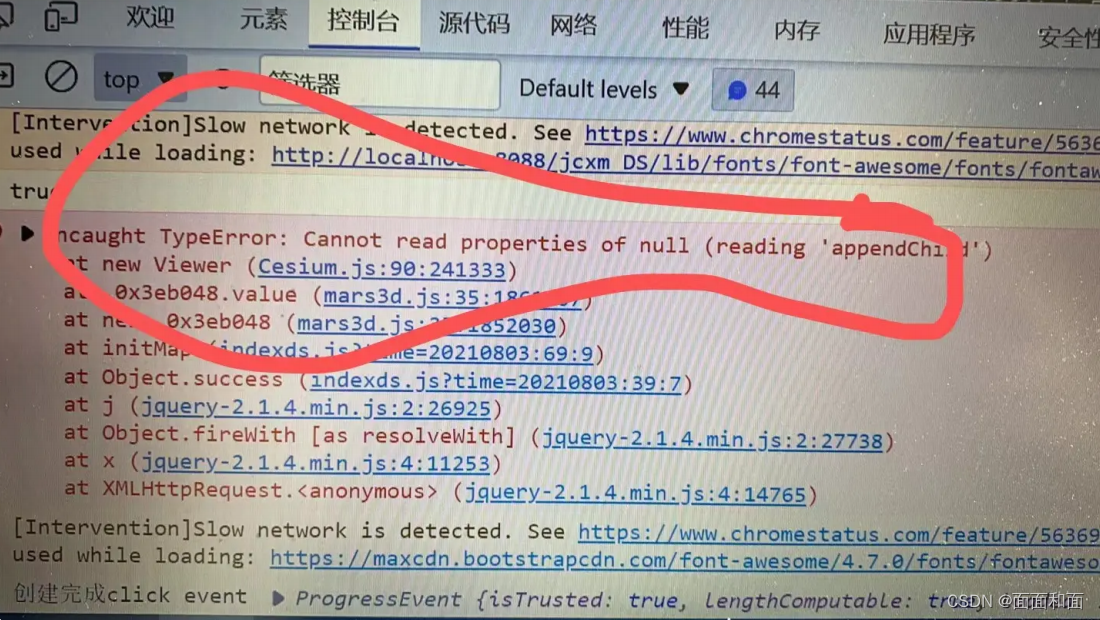
mars3d基础项⽬常⻅报错
1.在⼤家使⽤mars3d基础项⽬的时候经常遇到这个报错,截图如下 回答: 1.原因是因为使⽤了cnpm安装依赖,导致了⼀些依赖问题 2.解决⽅式也很简答,重新使⽤ npm 或 yarn 或 pnpm安装依赖即可 2.本地加载地图时,出现报错回…...
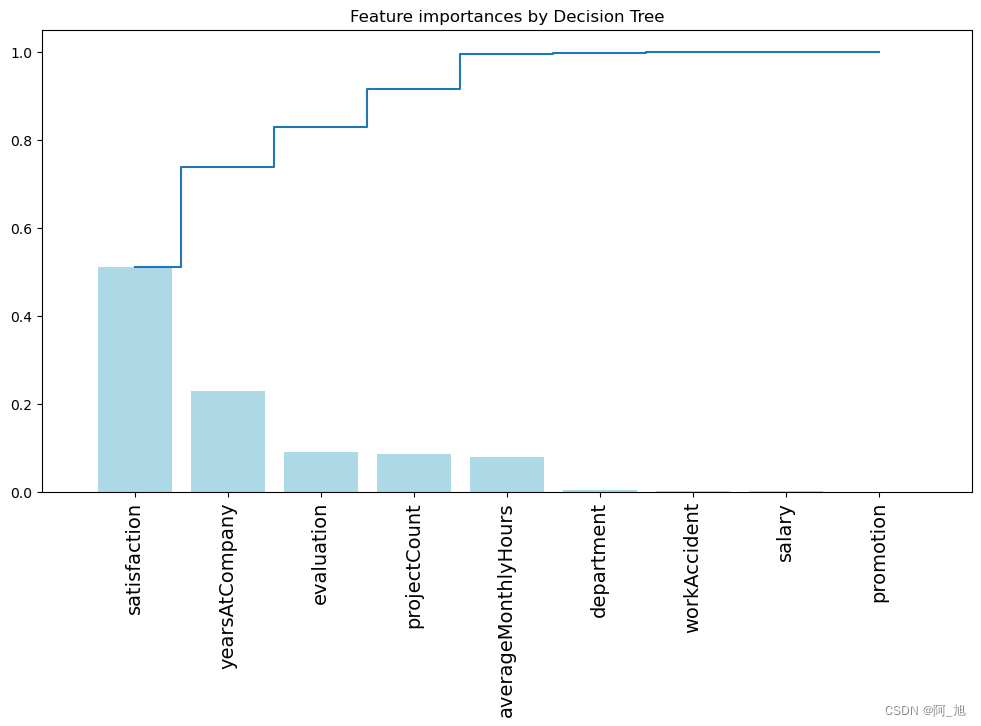
【阿旭机器学习实战】【35】员工离职率预测---决策树与随机森林预测
【阿旭机器学习实战】系列文章主要介绍机器学习的各种算法模型及其实战案例,欢迎点赞,关注共同学习交流。 本文的主要任务是通过决策树与随机森林模型预测一个员工离职的可能性并帮助人事部门理解员工为何离职。 目录1.获取数据2.数据预处理3.分析数据3.…...

Python学习-----模块4.0(json字符串与json模块)
目录 1.json简介: 2.json对象 3.json模块 (1)json.dumps() 函数 (2)json.dumps() 函数 (3)json.loads() 函数 (4) json.load() 函数 4.总结: 1.json简介: SON(…...

open3d最大平面检测,平面分割
1.点云读入 读入文件(配套点云下载链接) # 读取点云 pcd o3d.io.read_point_cloud("point_cloud_00000.ply")配套点云颜色为白色,open3d的点云显示默认背景为白色,所以将点云颜色更改为黑色 pcd.colors o3d.utilit…...
)
【C++】4.类和对象(下)
1.再谈构造函数 1赋值 class Date { public:Date(int year, int month, int day){_year year;_month month;_day day;}private:int _year;int _month;int _day; };构造函数体中的语句只能将其称作为赋初值,而不能称作初始化。因为初始化只能初始化一次…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
