人工智能在教育上的应用2-基于大模型的未来数学教育的情况与实际应用
大家好,我是微学AI ,今天给大家介绍一下人工智能在教育上的应用2-基于大模型的未来数学教育的情况与实际应用,随着人工智能(AI)和深度学习技术的发展,大模型已经开始渗透到各个领域,包括数学教育。本文将详细介绍基于大模型在数学教育中的实际应用,随着AI技术的不断发展和进步,我们已经看到AI可以在诸如图像识别、自然语言处理等多个领域内提供强大的支持。其中一个最具潜力和前景广阔的领域就是教育。特别是,在复杂且抽象性高的数学教育领域,AI技术尤其显示出其独特优势。

一、背景
传统上,数学被认为是一门需要通过刻苦钻研和长时间实践才能掌握好的科目。然而,在过去几年里,我们已经看到了AI如何改变这种现状。基于大模型如ChatGPT,ChatGLM2,LLaMA,百川,通义千问等在数学教育上得以应用,并且取得了显著成效。
二、原理与方法
1. 人工智能数学原理
利用深度神经网络进行机器学习主要涉及以下几个核心概念:
1.向量空间:
对于任何输入(例如文本),机器都会将其转化为高维向量空间中的一个点。在数学上,我们可以将向量空间定义为一组具有加法和标量乘法两种运算的对象集合。这个定义可以表示为:
设 V V V是一个非空集合,如果对于所有 x , y ∈ V x, y \in V x,y∈V和所有标量 c ∈ R c \in \mathbb{R} c∈R或 C \mathbb{C} C,下列公理成立:
- x + y = y + x x + y = y + x x+y=y+x (交换律)
- ( x + y ) + z = x + ( y + z ) (x + y) + z = x + (y + z) (x+y)+z=x+(y+z) (结合律)
- 存在元素 0 ∈ V 0 \in V 0∈V使得 x + 0 = x x+0=x x+0=x
- 对每个 x ∈ V x\in V x∈V, 存在元素 − x ∈ V -x\in V −x∈V, 使得 x + ( − x ) = 0 x+(-x)=0 x+(−x)=0
- c ( x + y ) = c x + c y c(x+y)=cx+cy c(x+y)=cx+cy
- ( c + d ) x = c x + d x (c+d)x=cx+dx (c+d)x=cx+dx
- ( c d ) x = c ( d x ) (cd)x=c(dx) (cd)x=c(dx)
- 1 ∗ x = x 1*x=x 1∗x=x
则称 ( V , + , . ) (V,+,.) (V,+,.)是一个向量空间。
2.激活函数:
每一个神经元都有一个激活函数来决定它是否被“激活”。常见的激活函数有ReLU, Sigmoid, Tanh等。下面是这些函数的数学形式:
ReLU:
f ( x ) = m a x ( 0 , x ) f(x) = max(0,x) f(x)=max(0,x)
Sigmoid:
f ( x ) = 1 1 + e − x f(x) = \frac{1}{1+e^{-x}} f(x)=1+e−x1
Tanh:
f ( x ) = t a n h ( x ) = e x − e − x e x + e − x f(x) = tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} f(x)=tanh(x)=ex+e−xex−e−x
3.损失函数
损失函数衡量预测值与真实值之间的差异。例如均方误差(Mean Squared Error),交叉熵(Cross Entropy),Hinge Loss等。
均方误差(MSE):
L ( y , y ^ ) = 1 n ∑ i = 1 n ( y i − y i ^ ) 2 L(y,\hat{y})=\frac{1}{n}\sum_{i=1}^n(y_i-\hat{y_i})^2 L(y,y^)=n1i=1∑n(yi−yi^)2
交叉熵(Cross Entropy):
对于二分类问题:
L ( y , y ^ ) = − [ y l o g ( y ^ ) + ( 1 − y ) l o g ( 1 − y ^ ) ] L(y,\hat{y})=-[ylog(\hat{y})+(1-y)log(1-\hat{y})] L(y,y^)=−[ylog(y^)+(1−y)log(1−y^)]
多分类问题:
L ( y , y ^ ) = − ∑ i = 1 n y i l o g ( y i ^ ) L(y,\hat{y})=-\sum_{i=1}^ny_ilog(\hat{y_i}) L(y,y^)=−i=1∑nyilog(yi^)
4.反向传播算法:
反向传播算法用于计算神经网络中权重的梯度。在一个多层神经网络中,对于每一层 l l l和每个神经元 j j j,我们都可以计算出一个“误差项” δ j ( l ) \delta^{(l)}_j δj(l)来表示该神经元对最终输出误差的贡献程度。具体来说,我们有:
δ j ( L ) = ∂ ∂ z j ( L ) 1 2 ∣ ∣ y − h W , b ( x ) ∣ ∣ 2 = − ( y j − a j ( L ) ) ⋅ f ′ ( z j ( L ) ) \delta^{(L)}_j = \frac{\partial}{\partial z^{(L)}_j} \frac{1}{2} ||y - h_{W,b}(x)||^2 = -(y_j - a^{(L)}_j) \cdot f'(z^{(L)}_j) δj(L)=∂zj(L)∂21∣∣y−hW,b(x)∣∣2=−(yj−aj(L))⋅f′(zj(L))
其中 L L L是网络的输出层, h W , b ( x ) h_{W,b}(x) hW,b(x)是网络关于输入 x x x的输出,而 f ′ f' f′是激活函数的导数。然后我们再通过以下公式反向传播这些误差项:
δ i ( l ) = ( ∑ j = 1 s l + 1 W j i ( l + 1 ) δ j ( l + 1 ) ) f ′ ( z i ( l ) ) \delta^{(l)}_i = (\sum_{j=1}^{s_{l+1}} W_{ji}^{(l+1)} \delta_j^{(l+1)}) f'(z_i^{(l)}) δi(l)=(j=1∑sl+1Wji(l+1)δj(l+1))f′(zi(l))
其中 s l s_l sl表示第 l l l层的单元数(不包括偏置单元),并且这个等式必须对所有 l < L , i ∈ 1 , . . . , s l l< L, i \in { 1, ..., s_l } l<L,i∈1,...,sl成立。
最后,使用这些误差项计算权重和偏置项梯度:
∇ W j k J ( W , b ; x , y ) = a k l δ j ( l + 1 ) \nabla_{W_jk} J(W,b;x,y) = a_k^l \delta_j ^{(l+1)} ∇WjkJ(W,b;x,y)=aklδj(l+1)
∇ b i l J ( W , b ; x , y ) = δ i ( l ) \nabla_{b_i^l} J(W,b;x,y) = \delta_i ^{(l)} ∇bilJ(W,b;x,y)=δi(l)
在得到所有样本上损失函数关于权重和偏置的梯度之后,我们就可以用随机梯度下降(或其他优化算法)来更新权重和偏置了。
2. 模型训练框架
我们使用PyTorch框架来训练模型。这是一种基于Python的开源机器学习库,可以提供强大的GPU加速计算能力。
import torch
import torch.nn as nn
from torch.utils.data import DataLoader, Dataset
from transformers import AutoModel, AutoTokenizer
import gradio as gr
import mdtex2html
import torchtokenizer = AutoTokenizer.from_pretrained("THUDM/chatglm2-6b", trust_remote_code=True)
model = AutoModel.from_pretrained("THUDM/chatglm2-6b", trust_remote_code=True).half().cuda()
model = model.eval()class MathDataset(Dataset):def __init__(self, csv_file):self.data = pd.read_csv(csv_file)def __len__(self):return len(self.data)def __getitem__(self, idx):question = self.data.iloc[idx, 0]answer = self.data.iloc[idx, 1]return question, answerdataset = MathDataset('sample_data.csv')
dataloader = DataLoader(dataset, batch_size=32, shuffle=True)num_epochs =5
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters())for epoch in range(num_epochs):for i, (questions, answers) in enumerate(dataloader):output = model(questions)loss = criterion(output.view(-1), answers.view(-1))optimizer.zero_grad()loss.backward()optimizer.step()
三、创新点
基于大模型在数学教育上的应用系统主要体现以下五个创新点:
1.个性化教学:每位学生的理解能力、进度和偏好都是独特的。传统的课堂教育模式往往难以满足每个人的需求。然而,利用AI技术,我们可以为每位学生提供定制化的数学教程。例如,对于那些在几何方面表现出色但在代数方面有困难的学生,系统可以调整其课程内容,以强化他们在代数方面的理解和技能。
2.自适应反馈:传统上,老师需要花费大量时间批改作业并提供反馈。然而,在AI驱动下,我们可以根据每位学生答题情况实时调整题目难易程度和内容,并立即提供反馈。例如,如果一个学生连续回答正确几道高级微积分问题,则系统可能会推送更具挑战性的问题;相反地,如果他们在某一主题上表现得不够好,则系统可能会降低问题难度并给出更详细地步骤说明。
3.实时互动:与传统课堂教育相比,在线AI教师可以24小时全天候在线回答问题,并给出即时反馈。例如,在处理复杂数字计算或者解决复杂几何证明过程中遇到困惑时, 学生可以立即向AI询问并获取解答, 而无需等待下一次课程或寻找额外辅导。
4.无限扩展性:随着越来越多数据被输入到系统中, AI模型将会不断地进行自我更新和优化, 从而使得其理解深度和广度都得到增强。这意味着无论是初级算术还是高级微积分知识点, AI都能提供支持.
5.普适性:无论是在城市还是偏远地区, 只要有网络连接就可享受到这种服务。这对于那些因为各种原因(如地理位置、经济条件等)无法获得高质量教育的人来说,尤其重要。例如, 在偏远地区的学生也能通过这种方式接触到优秀的教学资源,从而提升他们的数学能力。
以上创新点将大模型应用于数学教育,使得个性化和高效的教育成为可能,并有望在全球范围内提升数学教育质量。
四、结论
本文是主要讲述了基于大模型在数学教育上的应用系统通过结合深度神经网络和大数据技术,在提高数学教育质量方面发挥了巨大作用。随着技术进步和更多资源投入,在未来可能会看到更多此类应用出现,为全球数学教育带来革命性的改变。
相关文章:

人工智能在教育上的应用2-基于大模型的未来数学教育的情况与实际应用
大家好,我是微学AI ,今天给大家介绍一下人工智能在教育上的应用2-基于大模型的未来数学教育的情况与实际应用,随着人工智能(AI)和深度学习技术的发展,大模型已经开始渗透到各个领域,包括数学教育。本文将详细介绍基于大模型在数学…...
C++学习day5
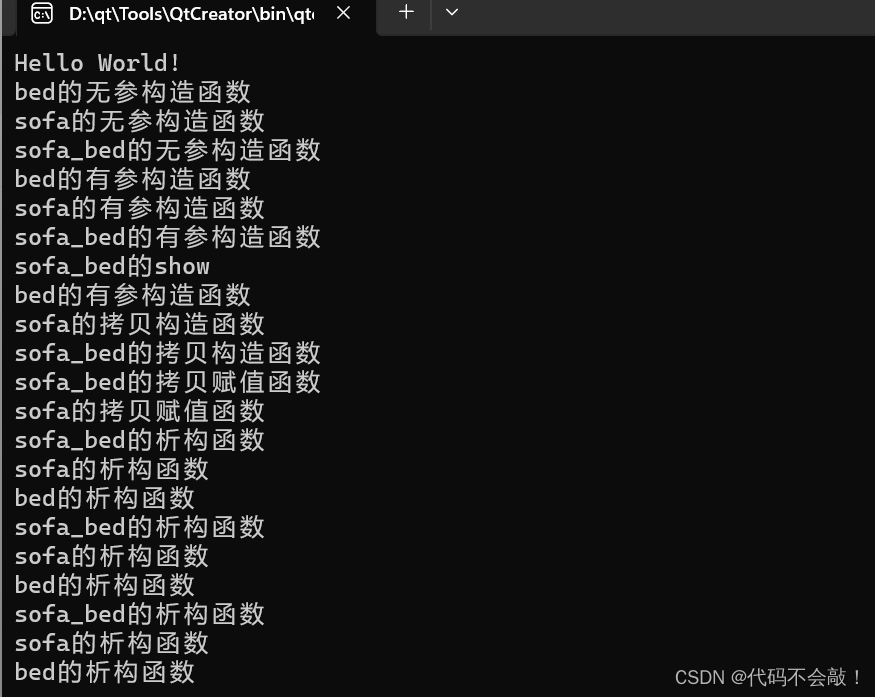
目录 作业: 1> 思维导图 2> 多继承代码实现沙发床 1>思维导图 2> 多继承代码实现沙发床 #include <iostream>using namespace std; //创建沙发类 class sofa { private:string sitting; public:sofa(){cout << "sofa的无参构造函数…...

1.软件开发-HTML结构-元素剖析
元素的嵌套 代码注释 ctrl/ URL url 统一资源定位符 一个给定的独特资源在web上的地址 URI...
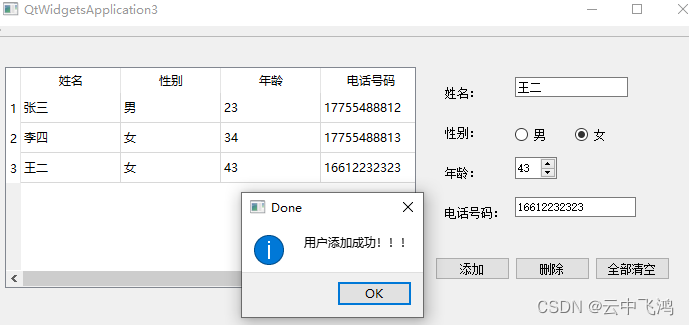
QTableWidget 表格增删数据
QTableWidgetQTableWidgetQTableWidget部分使用方法,如在表格中插入或删除一行数据以及清空表格数据等。在添加数据时,设置了条件判断如正则表达式,若用户输入的数据不合法,则添加失败并提示用户错误的地方,便于用户修…...
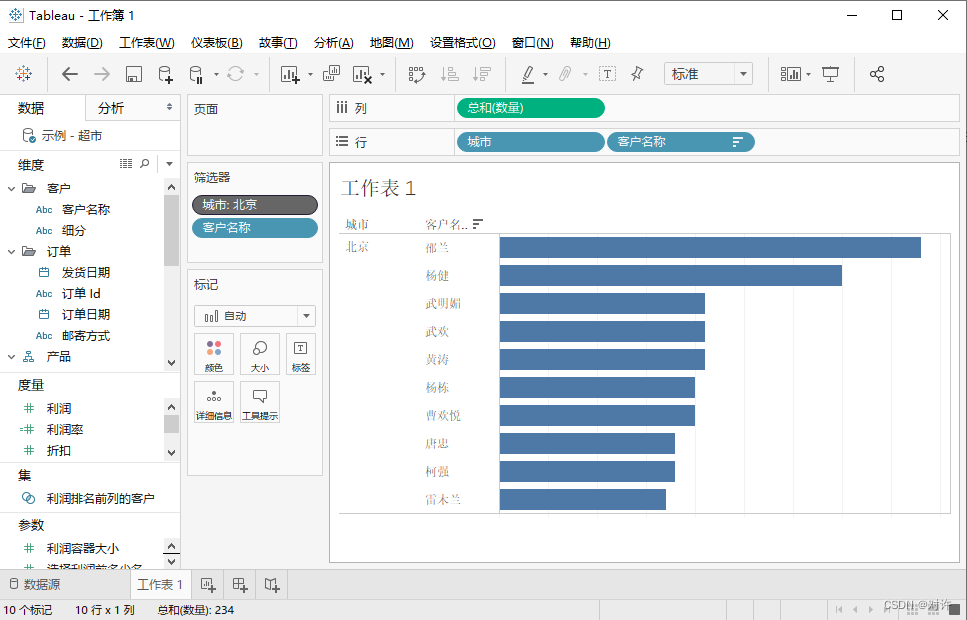
Tableau:商业智能(BI)工具
Tableau入门 1、Tableau概述2、Tableau Desktop2.1、初识Tableau Desktop2.2、Tableau工作区2.3、数据窗格与分析窗格2.4、功能区和标记卡2.4.1、列和行功能区2.4.2、标记卡2.4.3、筛选器功能区2.4.4、页面功能区2.4.5、附加功能区、图例、控件 3、Tableau视图4、Tableau工作簿…...

【gmail注册教程】手把手教你注册Google邮箱账号
手把手教你注册Google邮箱账号 写在前面: 要注意,注册Google邮箱必须要确保自己能够 科学上网,如果暂时做不到,请先进行相关学习。使用的手机号是大陆(86)的。 在保证自己能够科学上网后,在浏…...

docker版jxTMS使用指南:数据采集系统的高可用性
本文讲解4.6版jxTMS中数据采集系统的高可用性,整个系列的文章请查看:4.6版升级内容 docker版本的使用,请查看:docker版jxTMS使用指南 4.0版jxTMS的说明,请查看:4.0版升级内容 4.2版jxTMS的说明ÿ…...

vue如何禁止通过页面输入路径跳转页面
要禁止通过页面输入路径跳转页面,你可以使用Vue Router的导航守卫(navigation guards)来拦截导航并阻止不希望的跳转。 下面是一种常见的方法,你可以在全局导航守卫(global navigation guards)中实现这个功…...

mac,linux环境的基础工具安装【jdk,tomcat】
安装 一 linux环境一)、JDK安装卸载: 二)、 tomcat 安装1、[下载](https://mirrors.bfsu.edu.cn/apache/tomcat/tomcat-8/v8.5.63/bin/apache-tomcat-8.5.63.tar.gz)后,在目录 /usr/local/tomcat下,解压缩2、配置tomca…...
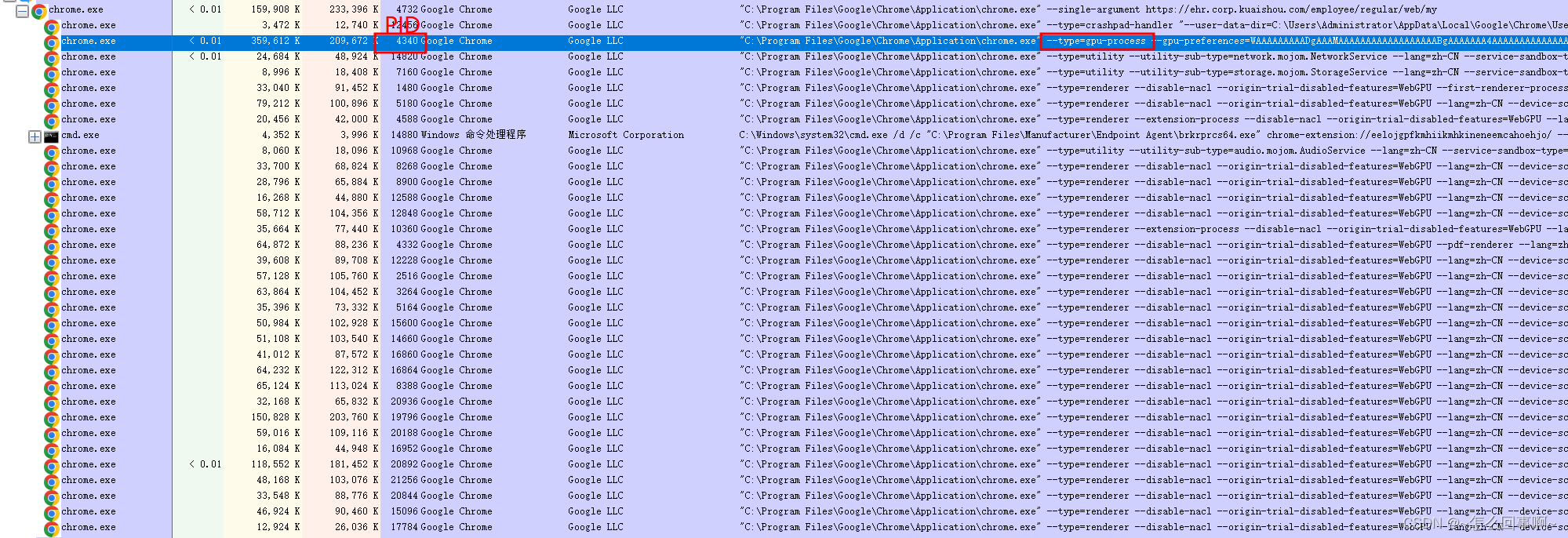
chrome窗口
chrome 窗口的层次: 父窗口类名:Chrome_WidgetWin_1 有两个子窗口: Chrome_RenderWidgetHostHWNDIntermediate D3D Window // 用于匹配 Chrome 窗口的窗口类的前缀。 onst wchar_t kChromeWindowClassPrefix[] L"Chrome_WidgetWin_…...

某快递公司Java一面
1.平衡二叉树和红黑树的区别? 平衡二叉树是一种二叉搜索树,其左子树和右子树的高度差不超过1,以确保在最坏情况下的查找效率是O(log n)。而红黑树是一种自平衡二叉搜索树,通过引入颜色标记(红色和黑色)来维…...

【C++ Primer Plus学习记录】指针——声明和初始化指针
指针用于存储值的地址,因此,指针名表示的地址。*运算符被称为间接值或解除引用运算符,将其应用于指针,可以得到该地址处存储的值。 例如,假设manly是一个指针,则manly表示的是一个地址,而*manl…...

切换至root用户时,命令提示符颜色为白色,如何修改?
当我切换至root用户时,发现命令提示符里的内容全部为白色,如图所示: 这让人看着不愉快,上网先搜索下解决方案:【切换到 root 账户字体全是白的,怎么改颜色啊】- 百度贴吧,但是这个解决方案只是…...

设计模式——17. 状态模式
1. 说明 状态模式(State Pattern)是一种行为设计模式,它允许一个对象在其内部状态发生改变时改变其行为。状态模式将对象的状态封装成不同的状态对象,并将状态切换时的行为委托给当前状态对象。这样,对象在不同状态下具有不同的行为,而无需在对象本身中使用大量的条件语…...
的软件开发)
系统架构设计:14 论软基于架构的软件设计方法(ABSD)的软件开发
目录 1 基于架构的软件设计(ABSD) 2 基于架构的软件开发过程 2.1 架构需求过程 2.2 架构设计过程</...

如何在 Spring Boot 中进行文件上传
在 Spring Boot 中进行文件上传 文件上传是Web应用程序中常见的功能之一,它允许用户将文件从客户端上传到服务器。Spring Boot提供了便捷的方式来处理文件上传,并且整合了Spring框架的强大功能,使文件上传变得相对简单。本文将介绍如何在Spr…...
Python 图形化界面基础篇:将应用程序打包为可执行文件
Python 图形化界面基础篇:将应用程序打包为可执行文件 引言 PyInstaller 简介步骤1:安装 PyInstaller 步骤2:创建 Python GUI 应用程序步骤3:使用 PyInstaller 打包应用程序 完整示例代码解释结论 引言 在开发完一个图形用户界面…...

Android 13.0 蓝牙遥控器确认键弹不出输入法的解决方法
1.概述 在android13.0设备定制化开发时,遥控器是使用红外遥控器,也有使用蓝牙遥控器的,所以出现的问题不一定相同,今天遇到个问题就是蓝牙遥控器在输入数据时弹不出输入法的问题 首选排除输入法的问题,安装其他的输入法,也是同样的问题,这样就确定是系统EditText控件相关…...

spring boot面试50问
目录 前言: 1. 什么是 Spring Boot? 2. 为什么要用SpringBoot? 3. SpringBoot与SpringCloud 区别? 4. Spring Boot 有哪些优点? 5. Spring Boot 的核心注解是哪个?它主要由哪几个注解组成的࿱…...
)
条例24~25(设计与声明)
条例24 若所有参数皆需要类型转换,请为此采用非成员函数 有时候让类型内成员函数支持隐式类型转换是不妥善的。比如当我们想在类内实现operator *() 模拟乘法的时候。通常情况下表现良好,但若你想额外实现混合式运算。例如 int…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
