bash上下键选择选项demo脚本
效果如下:
废话不多说,上代码:
#!/bin/bashoptions=("111" "222" "333" "444") # 选项列表
options_index=0 # 默认选中第一个选项
options_len=${#options[@]}echo "请用上下方向键进行选择,空格键选中/取消,回车键确认结果"# 定义一个数组来存储选中的结果
selected=()
for ((i=0; i<${options_len}; i++));doselected[$i]=0
done# 渲染选项列表
render_options() {for i in "${!options[@]}"; do# 首先渲染已经选中的选项if [ ${selected[$i]} -eq 1 ];thenif [ $i -eq $options_index ]; thenecho -e "\033[1;41;34m${options[$i]}\033[0m" # 已选中,已选择elseecho -e "\033[1;41;33m${options[$i]}\033[0m" # 已选中,未选择fielif [ $i -eq $options_index ]; thenecho -e "\033[1;34m${options[$i]}\033[0m" # 未选中,已选择elseecho "${options[$i]}" # 未选中,未选择fidone
}# 初始渲染
render_options# 为了让read能读到空格键
IFS_store=$IFS
IFS=''while true; doread -s -n 1 key # 读取单个按键输入,不显示在终端上case $key in"A") # 上箭头键if [ $options_index -gt 0 ]; thenoptions_index=$((options_index - 1))# 在第一行按上键,到最后一行elif [ $options_index -eq 0 ]; thenoptions_index=$((${options_len} - 1))fi;;"B") # 下箭头键if [ $options_index -lt $(( ${options_len} - 1 )) ]; thenoptions_index=$((options_index + 1))# 在最后一行按下键,到第一行elif [ $options_index -eq $(( ${options_len} - 1 )) ]; thenoptions_index=0fi;;" ") # 空格键# selected[$options_index]的值,0、1切换selected[$options_index]=$((1 - ${selected[$options_index]}));;"") # 回车键break;;esactput cuu ${options_len} # 光标移动回到选项列表的开头tput ed # 清除当前行render_options # 重新渲染选项列表
done# 恢复IFS变量
IFS=$IFS_store# 最后选中的所有结果
result=()
for ((i=0; i<options_len; i++));doif [ ${selected[$i]} -eq 1 ];thenresult+=(${options[$i]})fi
doneecho "选中:${result[@]}"相关文章:

bash上下键选择选项demo脚本
效果如下: 废话不多说,上代码: #!/bin/bashoptions("111" "222" "333" "444") # 选项列表 options_index0 # 默认选中第一个选项 options_len${#options[]}echo "请用上下方向键进行选择&am…...

cf 1886A
题目是输入一个数字,分解成三个数字的和,这三个数字都不相同,并且都不可以被三整除,如果存在输出YES并且输出任意一组可能的三个数字,否则输出NO 代码 #include<bits/stdc.h> using namespace std;int main() …...

Spring5应用之事务属性
作者简介:☕️大家好,我是Aomsir,一个爱折腾的开发者! 个人主页:Aomsir_Spring5应用专栏,Netty应用专栏,RPC应用专栏-CSDN博客 当前专栏:Spring5应用专栏_Aomsir的博客-CSDN博客 文章目录 参考文献前言事务…...

C# 搭建一个简单的WebApi项目23.10.10
一、创建Web API 1、创建一个新的web API项目 启动VS 2019,并在“开始页”选择“创建新项目”。或从“文件”菜单选择“新建”,然后选择“项目”。 选择ASP.NET Web应用程序(.NET Framework) 2.点击下一步,到这个页面时选择Web API。 3.选中…...
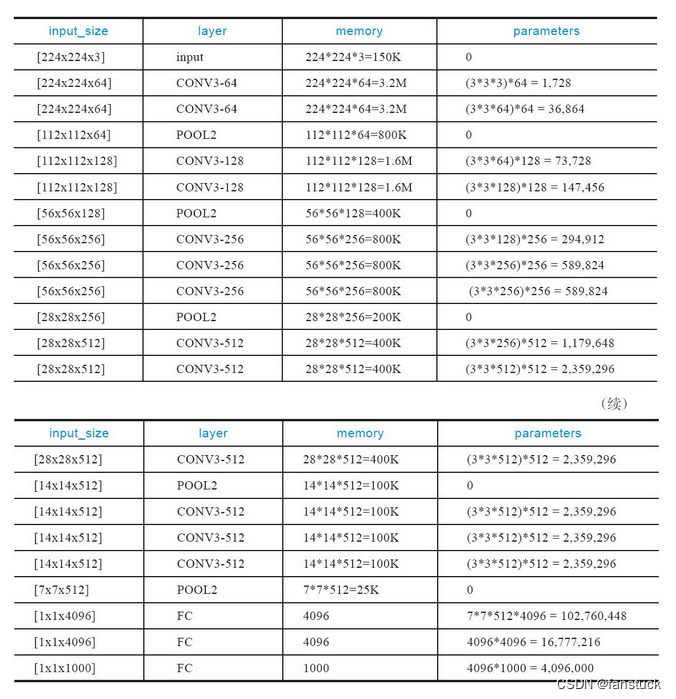
VGG卷积神经网络实现Cifar10图片分类-Pytorch实战
前言 当涉足深度学习,选择合适的框架是至关重要的一步。PyTorch作为三大主流框架之一,以其简单易用的特点,成为初学者们的首选。相比其他框架,PyTorch更像是一门易学的编程语言,让我们专注于实现项目的功能࿰…...

CentOS 7文件系统中的软链接和硬链接
软链接(Symbolic Link) 软链接,也称为符号链接,是一个指向另一个文件或目录的特殊类型的文件。它是一个指向目标文件的符号,就像快捷方式一样。软链接的创建和使用非常灵活,适用于各种情况。 创建软链接 …...
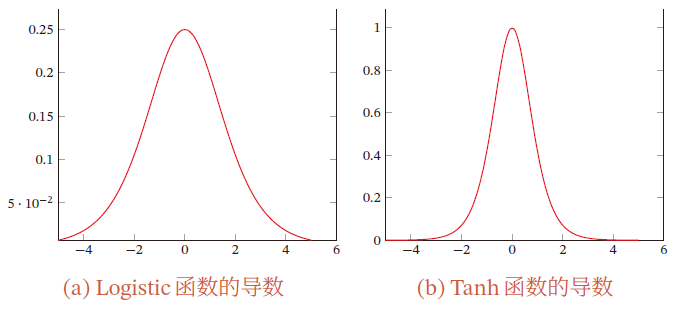
【AI】深度学习——前馈神经网络——全连接前馈神经网络
文章目录 1.1 全连接前馈神经网络1.1.1 符号说明超参数参数活性值 1.1.2 信息传播公式通用近似定理 1.1.3 神经网络与机器学习结合二分类问题多分类问题 1.1.4 参数学习矩阵求导链式法则更为高效的参数学习反向传播算法目标计算 ∂ z ( l ) ∂ w i j ( l ) \frac{\partial z^{…...
超简单的视频截取方法,迅速提取所需片段!
“视频可以截取吗?用相机拍摄了一段视频,但是中途相机发生了故障,录进去了很多不需要的片段,现在想截取一部分视频出来,但是不知道方法,想问问广大的网友,知不知道视频截取的方法。” 无论是工…...
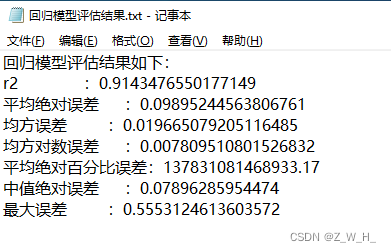
ArcGIS/GeoScene脚本:基于粒子群优化的支持向量机回归模型
参数输入 1.样本数据必须包含需要回归的字段 2.回归字段是数值类型 3.影响因子是栅格数据,可添加多个 4.随机种子可以确保每次运行的训练集和测试集一致 5.训练集占比为0-1之间的小数 6.迭代次数:迭代次数越高精度越高,但是运行时间越长…...

vue3组件的通信方式
一、vue3组件通信方式 通信仓库地址:vue3_communication: 当前仓库为贾成豪老师使用组件通信案例 不管是vue2还是vue3,组件通信方式很重要,不管是项目还是面试都是经常用到的知识点。 比如:vue2组件通信方式 props:可以实现父子组件、子父组件、甚至兄弟组件通信 自定义事件:可…...

Qt QPair
QPair 文章目录 QPair 摘要QPairQPair 特点代码示例QPair 与 QMap 区别 关键字: Qt、 QPair、 QMap、 键值、 容器 摘要 今天在观摩小伙伴撸代码的时候,突然听到了QPair自己使用Qt开发这么就,竟然都不知道,所以趁没有被人发…...
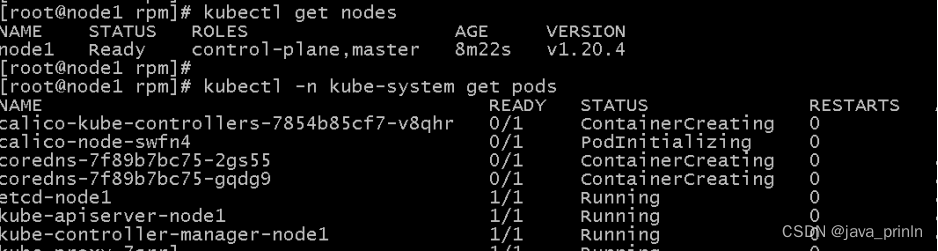
K8S云计算系列-(3)
K8S Kubeadm案例实战 Kubeadm 是一个K8S部署工具,它提供了kubeadm init 以及 kubeadm join 这两个命令来快速创建kubernetes集群。 Kubeadm 通过执行必要的操作来启动和运行一个最小可用的集群。它故意被设计为只关心启动集群,而不是之前的节点准备工作…...

ardupilot罗盘数据计算航向
目录 文章目录 目录摘要1.数据特点2.数据结论1.结论2.结论摘要 本节主要记录ardupilot 根据罗盘数据计算航向的过程。 如果知道了一组罗盘数据,我们可以粗略估计航向:主要后面我们所说的X和Y都是表示的飞机里面的坐标系,也就是X前Y右边,如果按照罗盘坐标系Y实际在左边。 我…...
)
第六章:最新版零基础学习 PYTHON 教程—Python 正则表达式(第一节 - Python 正则表达式)
在本教程中,您将了解RegEx并了解各种正则表达式。 常用表达为什么使用正则表达式基本正则表达式更多正则表达式编译的正则表达式 目录 元字符 为什么是正则表达式?...

docker安装Jenkins完整教程
1.docker拉取 Jenkins镜像并启动容器 新版本的Jenkins依赖于JDK11 我们选择docker中jdk11版本的镜像 # 拉取镜像 docker pull jenkins/jenkins:2.346.3-2-lts-jdk11 2.宿主机上创建文件夹 # 创建Jenkins目录文件夹 mkdir -p /data/jenkins_home # 设置权限 chmod 777 -R /dat…...

[CISCN 2019初赛]Love Math - RCE(异或绕过)
[CISCN 2019初赛]Love Math 1 解题流程1.1 分析1.2 解题题目代码: <?php //听说你很喜欢数学,不知道你是否爱它胜过爱flag if(!isset($_GET[c]))...
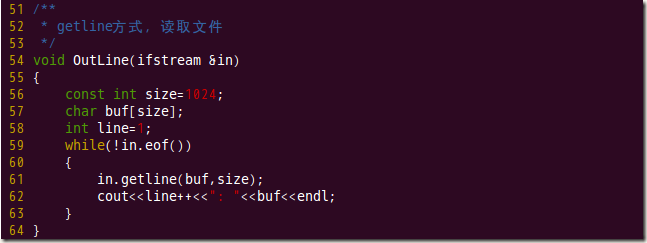
C++ 使用getline()从文件中读取一行字符串
我们知道,getline() 方法定义在 istream 类中,而 fstream 和 ifstream 类继承自 istream 类,因此 fstream 和 ifstream 的类对象可以调用 getline() 成员方法。 当文件流对象调用 getline() 方法时,该方法的功能就变成了从指定文件中读取一行字符串。 该方法有以下 2 种语…...
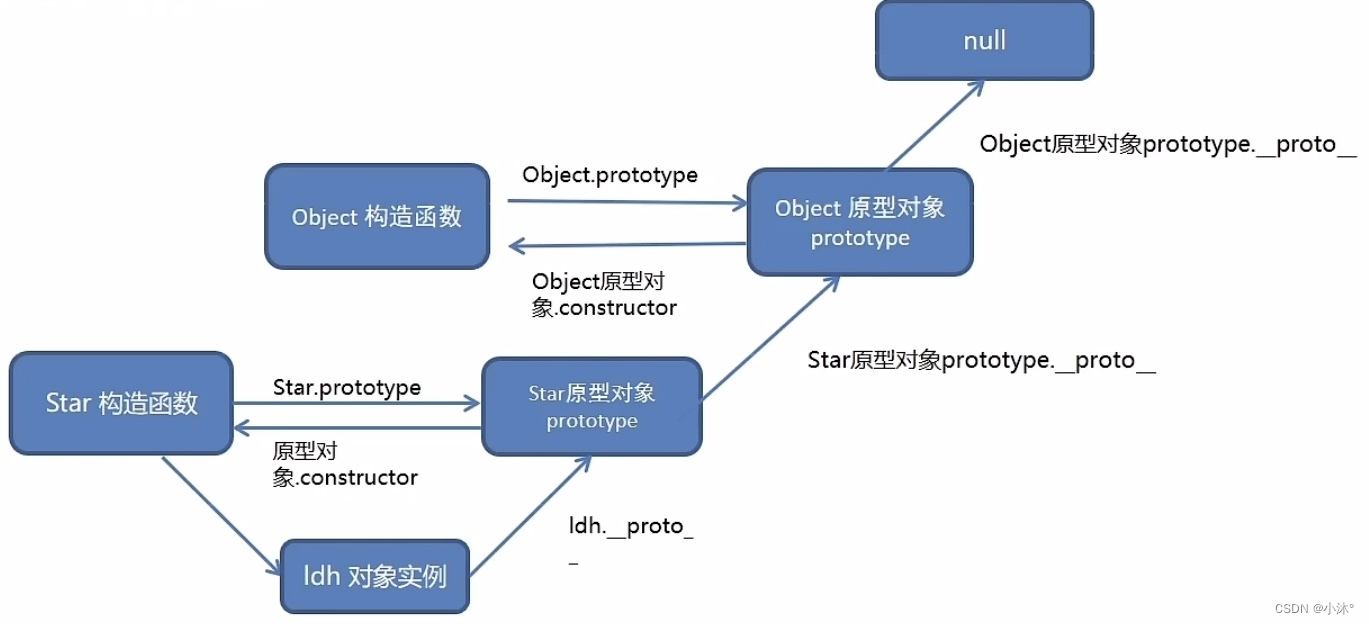
JS进阶-原型
原型 原型就是一个对象,也称为原型对象 构造函数通过原型分配的函数是所有对象所共享的 JavaScript规定,每一个构造函数都有一个prototype属性,指向另一个对象,所以我们也称为原型对象 这个对象可以挂载函数,对象实…...

虹科方案 | 汽车CAN/LIN总线数据采集解决方案
全文导读:现代汽车配备了复杂的电子系统,CAN和LIN总线已成为这些系统之间实现通信的标准协议,为了开发和优化汽车的电子功能,汽车制造商和工程师需要可靠的数据采集解决方案。基于PCAN和PLIN设备,虹科提供了一种高效、…...

HTML5+CSSDAY4综合案例一--热词
样式展示图: 代码如下: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>热词…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
