因子分析计算权重
因子分析两类权重计算方法总结

- 案例背景
疫情爆发以来,越来越多的人为了避免线下与人接触,选择了线上购买生活必需品。网购虽然方便快捷,但是随着订单压力的增加,物流问题也随之出现,近期有很多卖家收到物流投诉的问题。淘宝某网店想要使用因子分析研究物流服务质量不同维度所占权重的情况,采用随单进行问卷调查的方式,共收集到200份数据,其中14个项调查数据可分为可靠性、经济性、时间性、灵活性4个维度。具体维度划分见下表:

- 前期准备
在使用因子分析计算权重的前期,需要按照因子分析的流程完成因子分析适用性判断、对应关系调整以及因子命名这3项准备工作。
(1)因子分析适用性判断
因子分析适用性通过KMO值和Bartlett球形度检验进行判断;KMO值是一个用于检验是否适合因子分析的指标,一般大于0.6即说明数据适合进行因子分析。Bartlett球形度检验对应的p值小于0.05则说明适合进行因子分析。
(2)对应关系调整
分析14个指标与因子的对应关系;如果对应关系与预期4个维度基本一致,比如经过因子分析后隶属于“可靠性”这一维度的三个指标“包装完好”、“信息保密”、“退货包运费”确实属于“可靠性”这一维度,则说明对应关系良好;否则,则说明指标与因子对应关系需要进行调整。当指标与因子对应关系出现严重偏差的时候可以将指标做删除处理。关于对应关系调整这一部分内容,不是本篇文章讲解的重点内容,可以参考SPSSAU帮助手册进行学习https://spssau.com/helps/advancedmethods/factor.html。
(3)因子命名
在第二步指标项与因子对应关系调整好之后,就可以结合专业知识,对信息浓缩完成的4个因子进行因子命名。比如,“运费合理”、“个性化服务”、“退换货费用”、“误差处理”这四个指标可以代表物流服务的价格是否经济合理,那么就可以将提取出的因子命名为“经济性”。本案例在初始阶段已经预设将指标项分为可靠性、经济性、时间性、灵活性四个维度。
三、因子权重计算
因子权重计算是指经过因子分析后,信息浓缩为几个因子,要计算这几个因子的权重大小,即各个因子所占比重的大小。比如在本案例中,因子权重计算是指计算“可靠性”、“经济性”、“时间性”、“灵活性”这四个维度的权重值。因子权重计算主要利用下图所示表格进行计算,如下图:

(1)基本概念
- 特征根:
特征根在因子分析中被用来解释因子的总贡献,特征根越大,说明因子越重要。特征根一般还可用于自动确定因子最佳个数,通常以大于1作为标准(多数情况自行设置因子个数)。 - 方差解释率
方差解释率是因子提取的信息量;方差解释率=特征根/总分析项个数。比如上图中因子1的方差解释率=7.910/13=0.6084,意味着该因子共提取出这13个分析项60.845%的信息。 - 累计方差解释率
因子累计提取出的信息量 - 最大方差旋转法
最大方差旋转法是一种因子分析旋转方法,它的目标是使每个因子的方差尽可能大。这种方法的基本思想是将每个因子的载荷矩阵进行调整,使得每个因子的方差尽可能大。 - 旋转后方差解释率
经过最大方差旋转后因子的方差解释率。使用旋转后方差解释率,可以提高分析的准确性和可解释性。
(2)计算原理
因子权重计算主要使用旋转后方差解释率和旋转后累计方差解释率进行计算。因为在经过因子旋转后,更有利于应用现实语言描述所得因子,使公共因子更具有实际意义。可以更突出各个因子的典型代表变量是谁,这样更容易发觉因子的作用。旋转的目的是通过改变坐标轴位置,重新分配各个因子所解释方差比例,使其载荷系数更接近1或0,能更好地解释和命名变量。旋转后的因子不改变模型对数据的拟合程度,也不改变各个变量的公因子方差,使因子结构变得更简单。所以,使用旋转后方差解释率可以提高因子分析的可解释性。
(3)计算示例

从上表可知:4个因子旋转后的方差解释率分别是33.530%,32.248%,12.046%,10.571%,旋转后累积方差解释率为88.395%。旋转后方差解释率归一化,可以得到4个因子的权重,计算如下:
因子1(时间性)权重=33.530% / 88.395%=0.379
因子2(经济性)权重=32.248% / 88.395%=0.365
因子3(灵活性)权重=12.046% / 88.395%=0.136
因子4(可靠性)权重=10.571% / 88.395%=0.120
计算得到,关于该淘宝网店物流服务质量研究的四个维度:时间性、经济性、灵活性、可靠性的权重分别是0.379、0.365、0.136、0.120。
四、指标权重计算
因子权重计算完成后,还可以进行指标项权重计算。指标权重计算是指,所有指标项所占权重。比如在本例中“包装完好”、“信息保密”“退换货保障”等14个指标项各自所占的权重。或者可以将因子权重理解为一级指标权重,将指标权重理解为二级指标权重。计算指标权重,主要使用到两个指标,分别是线性组合系数和综合得分系数,下面将逐个进行说明。

- 线性组合系数
线性组合系数可用于表述信息浓缩的大小,计算线性组合系数,公式为:loading矩阵/Sqrt(eigen),即载荷系数除以对应特征根的平方根。
(2)综合得分系数
综合得分系数可用于衡量指标所占信息比重的大小,综合得分系数越大,说明指标所携带信息越大,指标权重越大。计算综合得分系数,公式为:累积(线性组合系数*方差解释率)/累积方差解释率,即线性组合系数分别与方差解释率相乘后累加,然后除以累积方差解释率;
如上图:可靠性1综合得分系数=(0.0898*33.53%+0.2706*32.25%+0.0951*12.05%+0.6573*10.57%)/(33.53%+32.25%+12.05%+10.57)=0.2244
(3)计算示例
计算指标权重,将综合得分系数进行归一化处理即得到各指标权重值;
如上图:可靠性1权重=(0.2244/∑综合得分系数)*100%=7.54%
可靠性2权重=(0.2340/∑综合得分系数)*100%=7.86%
其他指标权重计算过程同上。
注:上述loading矩阵,特征根eigen,方差解释率或累积方差解释率均为旋转后对应值
五、总结
因子权重计算与指标权重计算都可以通过SPSSAU因子分析输出的结果进行计算。因子权重使用旋转后方差解释率以及旋转后累计方差解释率进行计算;指标项权重使用归一化综合得分系数进行计算。虽然指标项计算过程略显复杂,但SPSSAU会在线性组合系数及权重结果这张表中自动输出权重值,大大简化了手动计算的繁琐步骤。
如果使用了因子分析计算因子权重后,不想再使用因子分析计算指标项权重,那么可以使用其他权重计算方法进行指标项权重的计算。例如,可以使用熵值法进行指标项权重计算,那么这里就使用了因子分析与熵值法两种计算权重的方法,可以丰富研究方法。
相关文章:

因子分析计算权重
因子分析两类权重计算方法总结 案例背景 疫情爆发以来,越来越多的人为了避免线下与人接触,选择了线上购买生活必需品。网购虽然方便快捷,但是随着订单压力的增加,物流问题也随之出现,近期有很多卖家收到物流投诉的问题…...
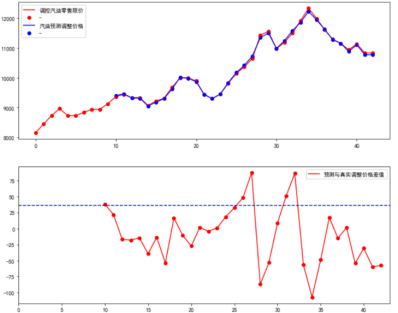
国家调控油价预测案例+源码
项目git地址:https://github.com/Boris-2021/Oil-price-control-forecast 使用已知的历史数据:日期、汇率、布伦特、WTI、阿曼原油价格,预测下一个调价周期中的汽油、柴油零售限价的调价价格。 一. 需求 1.1 需求说明 使用已知的历史数据&a…...

Gephi快速入门
Gephi快速入门1. 导入文件(Import file)2. 布局(Layout)3. 排序(Ranking)4. 指标(Metrics)5. 标签(Label)6. 社区发现(Community detection&#…...
GitHub
什么是 Github?GitHub是一个面向开源及私有软件项目的托管平台,因为只支持Git作为唯一的版本库格式进行托管,故名GitHub。一、常用词Watch:观察。如果watch了一个项目,之后这个项目有更新,你会在第一时间收到该项目更…...

QT基础入门【调试篇】QT远程部署与调试嵌入式ARM开发板
目录 一、环境配置 1、根据开发板完成交叉编译链以及GDB的配置(因开发板而异)...

可观测性最佳实践|阿里云事件总线 EventBridge 最佳实践
本文介绍如何把阿里云事件总线 EventBridge 的内容接入观测云平台,通过观测云强大的统一汇聚能力轻松获取阿里云事件,实时追踪最新的数据信息。 背景信息 事件总线 EventBridge 是阿里云提供的一款无服务器事件总线服务,支持阿里云服务、自定…...

设计模式-行为型
设计模式-行为型 行为型设计模式主要用于软件运行时复杂的流程控制。包含:模板方法模式、策略模式、命令模式、职责链模式、状态模式、观察者模式、中介者模式、迭代器模式、访问者模式、备忘录模式和解释器模式 模板方法模式 在软件设计时,很多时候系…...
Salesforce大揭秘!SaaS鼻祖不为人知的那些事!
Salesforce的世界无疑是广阔的。自从创始人Marc Benioff于1999年创立公司以来,Salesforce一直在打破CRM领域的界限,改变销售、营销和技术的格局。 作为全球领先的B2B科技公司之一,Salesforce和硅谷里的其他企业一样,缔造着一个关…...
Oracle——物化视图
文章目录含义物化视图的语法物化视图的创建1、自动刷新的物化事务 ON COMMIT2、非自动刷新的物化视图 ON demand关于手动刷新物化视图的删除资料参考含义 什么是物化视图? 物化视图,通俗点说就是物理化的视图。 什么叫物理化? 将视图以表结构…...

ur3+robotiq 2f 140配置moveit
ur3robotiq 2f 140配置moveit 参考链接1 参考链接2 官方配置movit教程 搭建环境: ubuntu: 20.04 ros: Nonetic sensor: robotiq_ft300 gripper: robotiq_2f_140_gripper UR: UR3 reasense: D435i 通过下面几篇博客配置好了ur3、力传感器、robotiq夹爪…...

LDO 芯片烫手,问题出在哪里?
设计失误的一个电路,该电路是数字电路的电源,为图方便对12V直接通过线性电源芯片降压到5V: 图1:线性电源降压12V转5V 几块电路板打样好后,测试均发现AMS1117-5.0芯片烫手,负载电流100mA多,也满…...

零日漏洞发展格局及防御策略
在过去的一年半中, 在野利用的零日漏洞数量持续飙升 ,这些软件制造商尚不知晓的漏洞正在被国家行为体黑客组织和勒索软件团伙滥用。 今年上半年,Google Project Zero统计了近20个零日漏洞,其中 大部分针对微软、苹果和谷歌构建的…...

RabbitMQ 可用磁盘空间报警
概要当磁盘可用空间低于设定的值(默认50M),将触发警报,并阻塞所有生产者。这目标是为了避免填满整个磁盘,这将导致所有节点上的写入操作失败,并可能导致RabbitMQ停止服务。如何工作为了减少磁盘被填满的风险…...

Web前端学习:二
二一:文字font-size样式 font-size:**px 控制文字大小,可精准控制大小 默认样式medium,中等的 large,大一号 x-large,再大一号 xx-large,再大一号 small,小一号 <!DOCTYPE html…...

【第一章 计算机网络体系结构,标准化工作相关组织,性能指标,分层结构,OSI参考模型】
第一章 计算机网络体系结构,标准化工作相关组织,性能指标,分层结构,OSI参考模型 1.计算机网络: (1)概念: ①计算机网络是将一个分散的、具有独立功能的计算机系统,通过通…...
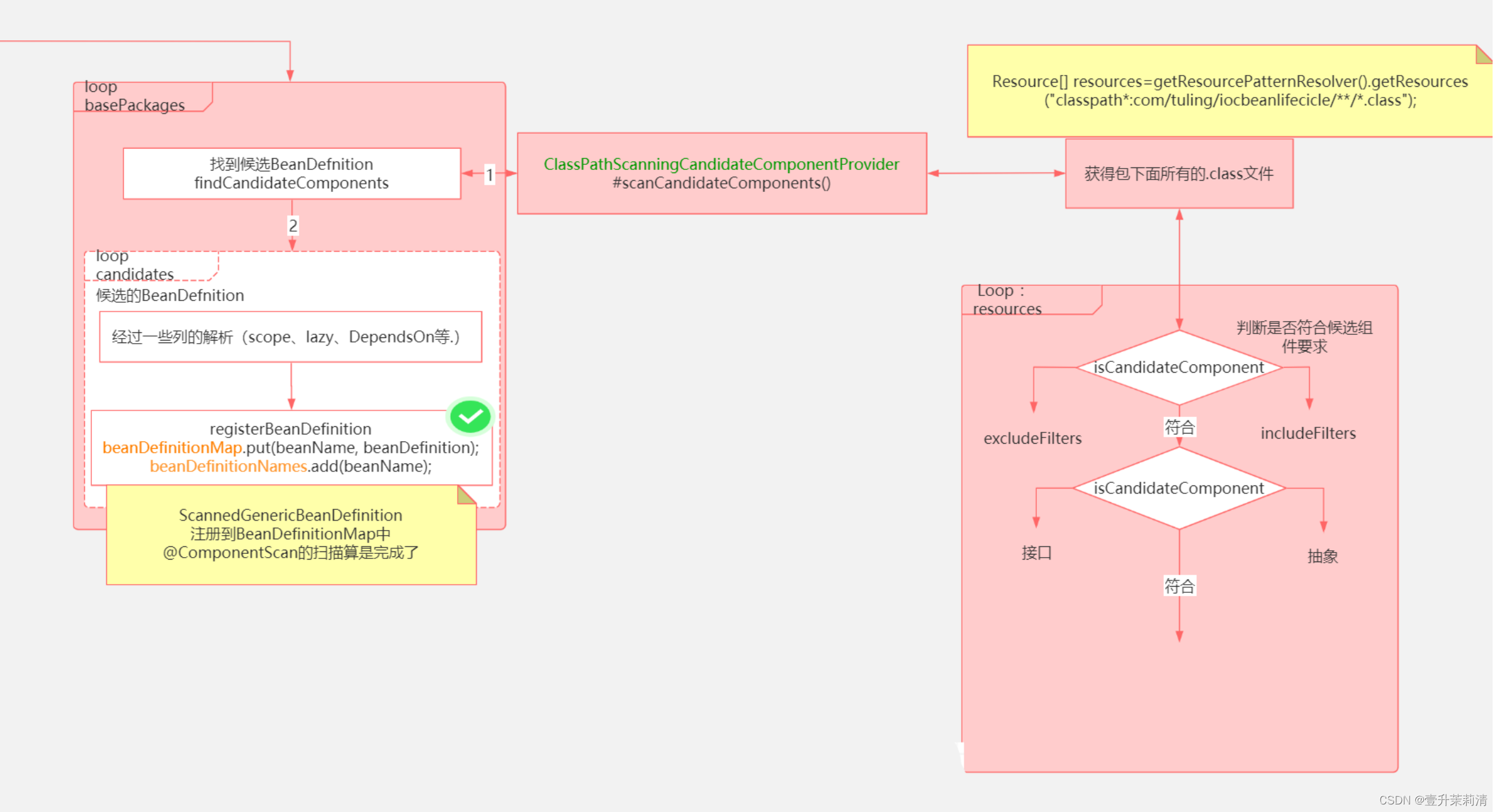
SpringIOC源码解析
Spring深度学习(一)——IOC的设计理念Spring的核心思想——IOCSpring流程图DEMO编写Spring IoC容器的加载过程实例化化容器:AnnotationConfigApplicationContext实例化建BeanDefinition读取器: AnnotatedBeanDefinitionReaderBean…...
【Jupyter Notebook的简单入门使用】
【Jupyter Notebook的简单入门使用】简单介绍安装与配置简单使用Markdown关闭简单介绍 Jupyter官网 Jupyter Notebook 介绍 简单来讲,它是一个网页应用,可以进行文档编写,甚至运行 py 代码等功能 安装与配置 下载合适版本的 python &#…...

@Component@Import@Bean加载顺序解析
【前言】 我们在使用Spring注入Bean对象时,会使用不同注解,比如Component Service Controller Import Bean等。由于Service Controller 等都可以归为Component,那么Component 和Import 、Bean是何时被加载的,以及他们之间的顺序呢…...
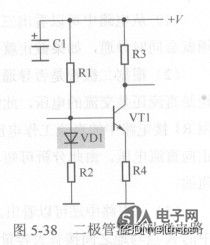
二极管温度补偿电路工作原理分析
众所周知,PN结导通后有一个约为0.6V(指硅材料PN结)的压降,同时PN结还有一个与温度相关的特性:PN结导通后的压降基本不变,但不是不变,PN结两端的压降随温度升高而略有下降,温度愈高其…...

【C语言】多线程之条件竞争
多线程(三)条件竞争并发程序引起的共享内存的问题死锁互斥锁机制生产者消费者模型信号量机制解决:条件竞争 #include<stdio.h> #include<stdlib.h> #include<pthread.h> void* Print(char* str){printf("%s ",s…...

UE NavigationSystem的相关实现
导航数据的构建流程导航数据的收集导航系统中绑定了Actor、Component注册完成以及取消时的委托,通过这些委托把数据及时更新到导航系统的八叉树结构中导航系统的辅助结构DefaultOctreeController、DefaultDirtyAreasController分别承担了空间数据查询和置脏区域重新…...
Java 继承
文章目录1. 继承概述2. 变量的访问特点3. super 关键字4. 构造方法的访问特点5. 成员方法的访问特点6. 方法重写7. 继承案例1. 继承概述 继承是面向对象三大特征之一。可以使得子类具有父类的属性和方法,还可以在子类中重新定义,追加属性和方法。 publ…...

Python学习笔记8:异常
异常 一些内置的异常类 类名描述Exception几乎所有的异常类都是从它派生而来的AttributeError引用属性或给它赋值失败时引发OSError操作系统不能执行指定的任务(如打开文件)时引发,有多个子类IndexError使用序列中不存在的索引时引发&#…...

python保留小数函数总结
python保留小数——‘%f’‘%.nf’% x(定义的变量) 例子:a 82.16332 print(%.1f% a) print(%.2f% a) print(%.3f% a) print(%.4f% a) print(%.10f% a)输出结果python保留小数——format()函数Python2.6 开始ÿ…...

狐狸优化算法(Matlab代码实现)
👨🎓个人主页:研学社的博客💥💥💞💞欢迎来到本博客❤️❤️💥💥🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密…...

浏览器自动化框架沦为攻击者的工具
5月27日消息,安全公司Team Cymru的研究人员表示,越来越多的威胁参与者正在使用免费的浏览器自动化框架作为其攻击活动的一部分。 研究人员表示,该框架的技术准入门槛故意保持在较低水平,以创建一个由内容开发者和贡献者组成的活跃…...

SQL必备知识(自用)
数据库基础知识sql和mysql的区别:数据库查询大全(select)1、select 字段名 from 表;2、In查询:用于过滤你所需要查询的内容3、范围查询:between4、模糊查询:like5、查询空值/非空:is…...
BI工具术语表大全:从字母A-Z全面收录
谈到商业智能行业,变革是不可避免的。为了跟上步伐,各种各样的BI 解决方案正在快速迭代更新,以满足企业的数字化需求,那么市场上BI 工具种类繁杂,到底如何选择适合功能全面、满足自己企业运转情况的、合适的BI 工具呢&…...
vue3 + vite + ts 集成mars3d
vue3 vite ts 集成mars3d 文章目录vue3 vite ts 集成mars3d前言一、创建一个vue3 vite ts项目二、引入mars3d相关依赖三、vite.config.ts 相关配置四、 新建DIV容器 创建地图前言 使用mars3d过程中,需要集成mars3d到自己的项目中,mars3d开发教程…...
跨境卖家必看的沃尔玛Walmart商家入驻教程
沃尔玛Walmart作为作为全球连锁超市的鼻祖,有不可比拟的知名度。当沃尔玛从线下延伸到线上后,就成为一个自带IP与流量的线上平台,在全世界都拥有数量庞大的消费者群体。所以龙哥就结合自己注册Walmart的过程给大家详细讲解一下。 Walmart卖家…...
