《动手学深度学习 Pytorch版》 8.4 循环神经网络
8.4.1 无隐状态的神经网络
对于无隐藏装态的神经网络来说,给定一个小批量样本 X ∈ R n × d \boldsymbol{X}\in\mathbb{R}^{n\times d} X∈Rn×d,则隐藏层的输出 H ∈ R n × h \boldsymbol{H}\in\mathbb{R}^{n\times h} H∈Rn×h 通过下式计算:
H = ϕ ( X W x h + b h ) \boldsymbol{H}=\phi(\boldsymbol{XW}_{xh}+\boldsymbol{b}_h) H=ϕ(XWxh+bh)
- ϕ \phi ϕ 是隐藏层的激活函数
- n n n 是批量大小
- d d d 是输入维度
- W x h ∈ R d × h \boldsymbol{W}_{xh}\in\mathbb{R}^{d\times h} Wxh∈Rd×h 是隐藏层权重
- b h ∈ R 1 × h \boldsymbol{b}_h\in\mathbb{R}^{1\times h} bh∈R1×h 是偏置参数
- h h h 是隐藏层数目。
接下来将隐藏变量 H \boldsymbol{H} H 作为输出层的输入:
O = H W h q + b q \boldsymbol{O}=\boldsymbol{HW}_{hq}+\boldsymbol{b}_q O=HWhq+bq
- O ∈ R n × q \boldsymbol{O}\in\mathbb{R}^{n\times q} O∈Rn×q 是输出变量
- H W h q ∈ R h × q \boldsymbol{HW}_{hq}\in\mathbb{R}^{h\times q} HWhq∈Rh×q 是权重参数
- b q ∈ R 1 × q \boldsymbol{b}_q\in\mathbb{R}^{1\times q} bq∈R1×q 是输出层的偏置参数。
如果是分类问题,则可以用 s o f t m a x ( O ) softmax(\boldsymbol{O}) softmax(O) 计算输出的概率分布,此处无需多言。
8.4.2 有隐状态的循环神经网络
引入隐状态后,情况就完全不同了。具体地说,当前时间步隐藏变量由当前时间步的输入与前一个时间步的隐藏变量一起计算得出:
H t = ϕ ( X t W x h + H t − 1 W h h + b h ) \boldsymbol{H}_t=\phi(\boldsymbol{X}_t\boldsymbol{W}_{xh}+\boldsymbol{H}_{t-1}\boldsymbol{W}_{hh}+\boldsymbol{b}_h) Ht=ϕ(XtWxh+Ht−1Whh+bh)
- X t ∈ R n × d \boldsymbol{X}_t\in\mathbb{R}^{n\times d} Xt∈Rn×d 是时间步 t t t 的小批量输入
- H t ∈ R n × h \boldsymbol{H}_t\in\mathbb{R}^{n\times h} Ht∈Rn×h 是时间步 t t t 的隐藏变量
- H t − 1 \boldsymbol{H}_{t-1} Ht−1 是前一个时间步的隐藏变量
- W h h ∈ R h × h \boldsymbol{W}_{hh}\in\mathbb{R}^{h\times h} Whh∈Rh×h 是权重参数
由于在当前时间步中,隐状态使用的定义与前一个时间步中使用的定义相同,因此此计算是循环的(recurrent)。于是基于循环计算的隐状态神经网络被命名为循环神经网络(recurrent neural network)。
对于时间步 t t t,输出层的输出类似于多层感知机中的计算:
O t = H t W h q + b q \boldsymbol{O}_t=\boldsymbol{H}_t\boldsymbol{W}_{hq}+\boldsymbol{b}_q Ot=HtWhq+bq
在不同的时间步,循环神经网络也总是使用这些模型参数。因此,循环神经网络的参数开销不会随着时间步的增加而增加。

import torch
from d2l import torch as d2l
X, W_xh = torch.normal(0, 1, (3, 1)), torch.normal(0, 1, (1, 4))
H, W_hh = torch.normal(0, 1, (3, 4)), torch.normal(0, 1, (4, 4))
torch.matmul(X, W_xh) + torch.matmul(H, W_hh)
tensor([[-0.9743, 0.4619, -0.7949, 0.3287],[ 5.9413, 2.1961, 0.6053, 0.1704],[-1.0903, -0.2396, -1.0930, -0.8530]])
torch.matmul(torch.cat((X, H), 1), torch.cat((W_xh, W_hh), 0))
tensor([[-0.9743, 0.4619, -0.7949, 0.3287],[ 5.9413, 2.1961, 0.6053, 0.1704],[-1.0903, -0.2396, -1.0930, -0.8530]])
8.4.3 基于循环神经网络的字符级语言模型
以 “machine” 为例:

8.4.4 困惑度(Perplexity)
我们使用困惑度来评估模型。
一个更好的语言模型应该能让我们更准确地预测下一个词元,所以我们可以通过一个序列中所有的 n n n 个词元的 交叉熵损失的平均值 来衡量:
1 n ∑ t = 1 n − log P ( x t ∣ x t − 1 , … , x 1 ) \frac{1}{n}\sum^n_{t=1}-\log{P(x_t|x_{t-1},\dots,x_1)} n1t=1∑n−logP(xt∣xt−1,…,x1)
由于历史原因,自然语言处理的科学家更喜欢使用困惑度(perplexity)的。简而言之,它是上式的指数:
exp ( − 1 n ∑ t = 1 n log P ( x t ∣ x t − 1 , … , x 1 ) ) \exp\left(-\frac{1}{n}\sum^n_{t=1}\log{P(x_t|x_{t-1},\dots,x_1)}\right) exp(−n1t=1∑nlogP(xt∣xt−1,…,x1))
练习
(1)如果我们使用循环神经网络来预测文本序列中的下一个字符,那么任意输出所需的维度是多少?
啥叫“任意输出”?输出应该和输入是一个形状。
(2)为什么循环神经网络可以基于文本序列中所有先前的词元,在某个时间步表示当前词元的条件概率?
因为每个时间步的输入都有上一个时间步的输出。
(3)如果基于一个长序列进行反向传播,梯度会发生什么状况?
更容易出现梯度消失或者梯度爆炸。
(4)与本节中描述的语言模型相关的问题有哪些?
略。
相关文章:

《动手学深度学习 Pytorch版》 8.4 循环神经网络
8.4.1 无隐状态的神经网络 对于无隐藏装态的神经网络来说,给定一个小批量样本 X ∈ R n d \boldsymbol{X}\in\mathbb{R}^{n\times d} X∈Rnd,则隐藏层的输出 H ∈ R n h \boldsymbol{H}\in\mathbb{R}^{n\times h} H∈Rnh 通过下式计算: …...

什么是物联网阀控水表?
物联网阀控水表是一种新型的水表,结合了物联网技术和传统水表的功能,可以实现对水的计量、控制和管理。随着人们对水资源的日益重视,物联网阀控水表的应用越来越广泛,为水资源的合理利用和管理提供了有效手段。 物联网阀控水表是由…...
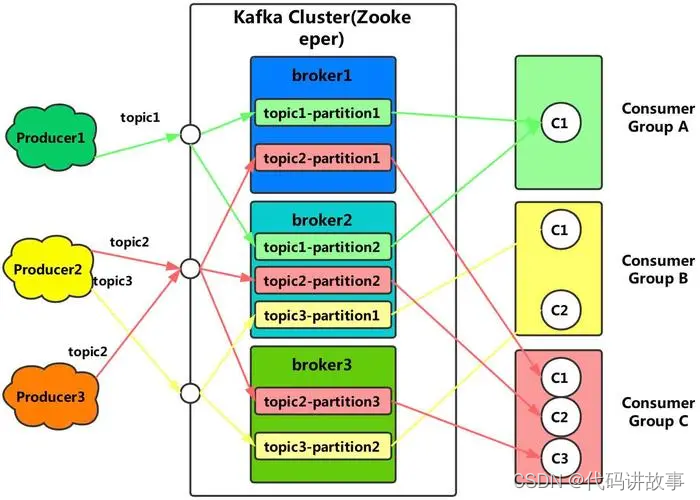
Kafka 开启SASL/SCRAM认证 及 ACL授权(一)认证
Kafka 开启SASL/SCRAM认证 及 ACL授权(一)认证。 kafka安全涉及3部份:传输加密,用户认证与授权,ZK开启ACL(Zookeeper存储了kafka的元数据以及用户信息,默认不开启acl所有用户可改,内网环境机器不对外开放可考虑使用默认不开启ZK ACL)。 官网地址:https://kafka.ap…...
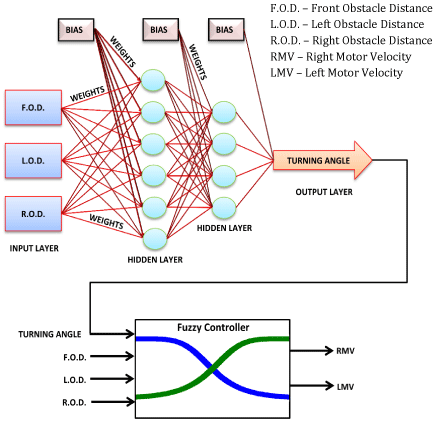
关于智能控制领域中模糊控制算法的概述
智能控制领域中的模糊控制算法是一种基于模糊逻辑的控制策略,它通过对模糊集合的刻画来处理模糊信息,从而获得模糊输出并进行控制。模糊控制算法在实际控制工程中具有良好的应用前景,它不但具有较强的鲁棒性和适应性,而且可以为复…...

剖析伦敦银最新价格走势图
国际金融市场瞬息万变,伦敦银的价格走势会受到诸多因素的影响,比如重要经济数据的公布,国际间的政治博弈,突发的政经大事,都可以令白银价格的走势,在短时间内暴涨暴跌的情况。 要在伦敦银市场实现良好的收益…...
)
通用人工智能技术(深度学习,大模型,Chatgpt,多模态,强化学习,具身智能)
目录 前言 1.通用人工智能 1.1 生物学分析 1.2具身智能 1.2.1当前的人工智能的局限 1.2.2 具身智能实现的基础 1.2.3 强化学习(决策大模型) 2.结论 往期文章 参考文献 前言 目前的人工智能实质上只是强人工智能,或者说单个领域的通…...

makefile的特性-部分语法记录
1.变量定义 1.1 来实现a1 $(a2)a2 lib.o1.2 : 来实现, 这种不能通过后面的变量来定义a1 : $(a2) b.0a2 : lib.o1.3 来实现a1 b.0a2 a11.4 ? 来实现,这种方式前面如果定义了,后面定义则无效a1 : a.oa1 ? lib.o //结果 a1 a.o 2.文件查找 2.1 VPATH 目录…...

【Java 进阶篇】JavaScript 正则表达式(RegExp)详解
JavaScript 正则表达式,通常简写为 RegExp,是一种强大的文本匹配工具,它允许你通过一种灵活的语法来查找和替换字符串中的文本。正则表达式在编程中用途广泛,不仅限于 JavaScript,在许多编程语言中也都有类似的实现。 …...

51单片机之串口通信例程
51单片机之串口通信例程 简介原理例程 简介 串行通信是指使用一条数据线,将数据一位一位地依次传输,每一位数据占据一个固定的时间长度。在串行通信中,数据可以以字符为单位进行传输,也可以以帧为单位进行传输。 在51单片机中&a…...
一键启动脚本)
Hadoop高可用集群(HA)一键启动脚本
高可用集群启动时,需要分别在每个节点上都执行zkServer.sh start启动zookeeper,这个过程比较麻烦,并且当我们节点增多时,这个过程无疑不增加了我们的工作量,因此我们可以写一个一键启动所有节点zookeeper的脚本 脚本实…...
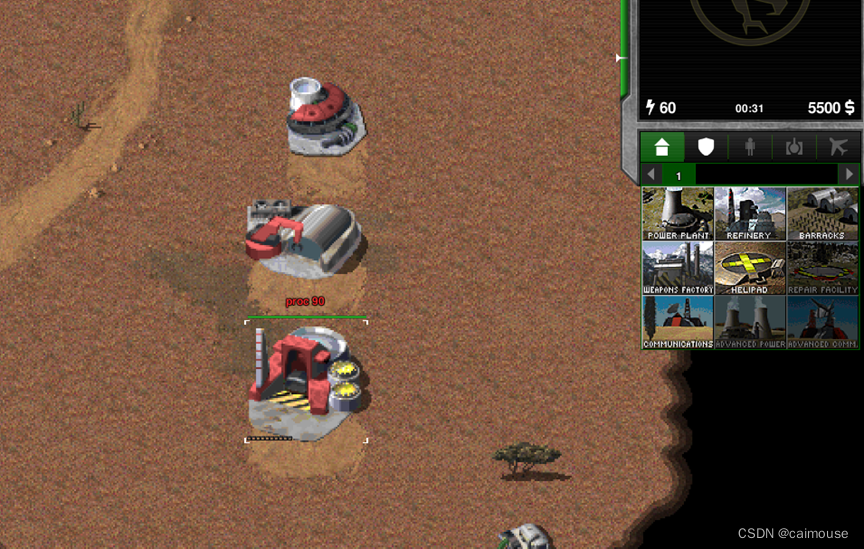
C#开发的OpenRA游戏之金钱系统(1)
C#开发的OpenRA游戏之金钱系统(1) 设计一个游戏,肯定要有一个唯一的资源,用这个资源来管理整个游戏的进度,以及相互争夺的焦点。在OpenRA里,就是使用矿产资源。所以在地图上分布几个矿场,玩家就需要相互争夺矿场,谁开采多谁就更有钱,谁有钱了就可以升级更好的科技,以…...
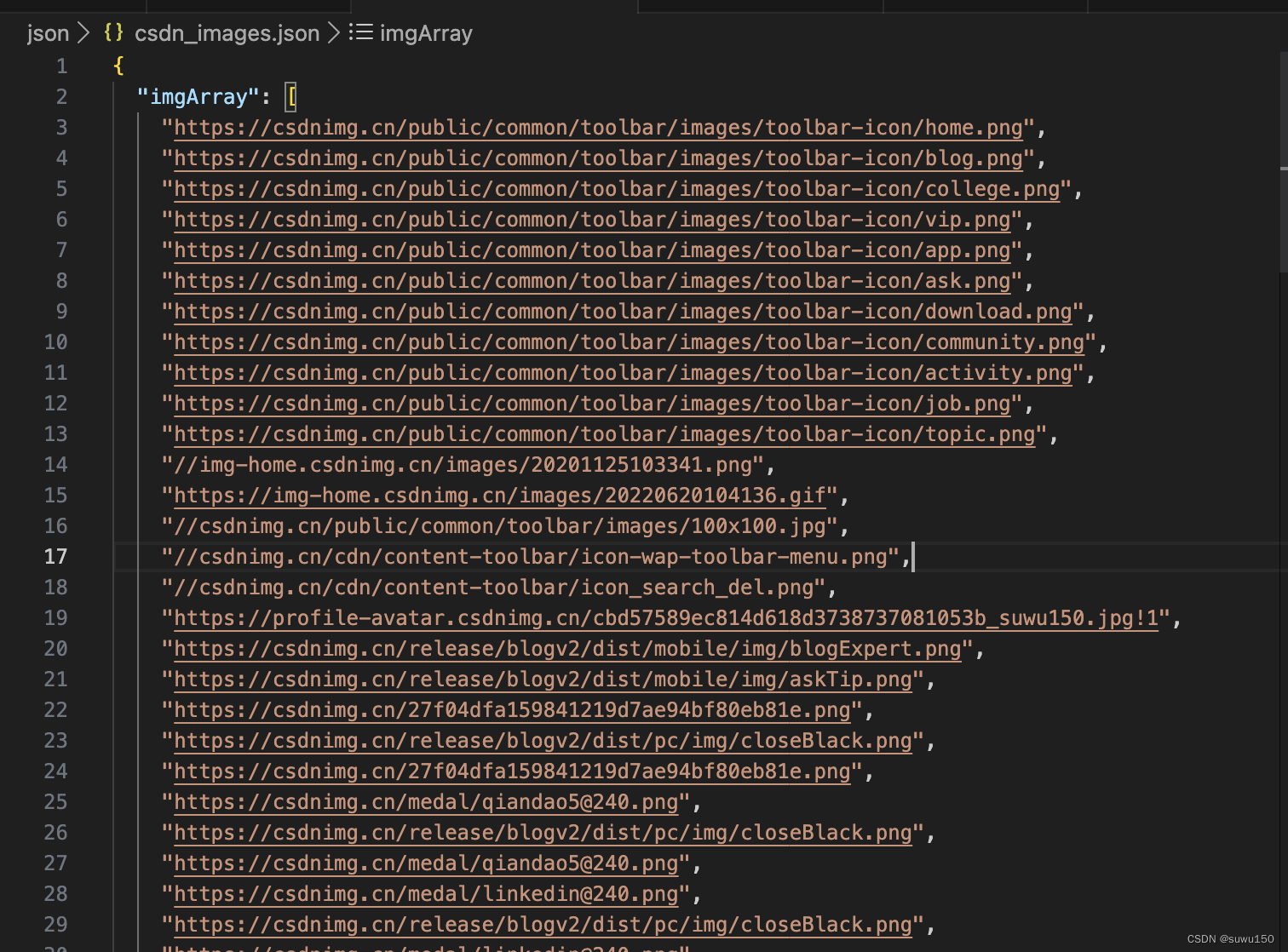
Puppeteer监听网络请求、爬取网页图片(二)
Puppeteer监听网络请求、爬取网页图片(二) Puppeteer监听网络请求、爬取网页图片(二)一、爬取需求二、实现讲解三、效果查看 一、爬取需求 首先打开浏览器,打开指定网站监听网站发出的所有请求,记录请求&a…...
GoLang连接mysql数据库
跟着文档走GORM 指南 | GORM - The fantastic ORM library for Golang, aims to be developer friendly. 1.使用命令拉取 go get -u gorm.io/gorm go get -u gorm.io/driver/sqlite2.开始使用 package mainimport ("fmt""github.com/gin-gonic/gin"&…...

软件工程与计算总结(八)软件设计基础
一.设计思想的发展 1958:软件这个名词第一次在公开刊物上使用~60年代中后期and70年代前中期:结构化编程、逐步求精、自顶向下理念是程序设计主要方法70年代中后期and90年代:结构化设计方法、抽象数据类型、信息隐藏、封装、继承、多态等思想…...

someip 入门
什么是someip? SomeIP(Scalable Service-Oriented MiddlewarE over IP)是一种基于以太网的通信协议,用于汽车领域的通信。它允许不同的汽车电子控制单元(ECUs)之间通过网络进行通信,以便在车辆内…...

C# 使用Parallel去执行并行下载
直接上代码: //最大线程下载数量ParallelOptions options new ParallelOptions{MaxDegreeOfParallelism 5};public async Task DownloadMusicUrl(List<MusicTags> musicTags){DateTime currentTime DateTime.Now;DateTime startTime new DateTime(1970, 1…...

@Component 和 @Bean的区别
Component 和 Bean 是Spring框架中用于管理和配置依赖注入的关键注解,用于定义和管理Spring应用程序中的组件。 Component: Component 是一种泛用型的Spring注解,用于标识一个类为Spring组件。Spring会自动扫描所有带有Component 注解的类,并…...
百度测试开发工程师面试心得
百度测试开发实习生面试心得: 电话面试: 面试官:首先做一下自我介绍吧 我:我是***,来自什么大学,现在大三,在学校期间担任过部长,副主席等职务, 组织举办了很多比赛&…...
发现更多美景!XnViewMP for Mac/Windows 图片浏览软件
想要轻松快捷地浏览、管理和编辑您的照片吗?XnViewMP for Mac 是您的最佳选择!这款强大而多功能的图片浏览软件将给您带来全新的视觉体验。 借助 XnViewMP,您可以方便地浏览各种图片格式,包括JPEG、PNG、GIF等,并支持…...
城市广告牌安全传感器特点有哪些?
城市广告牌安全传感器特点有哪些? 在现代快节奏的都市生活中,城市的广告牌成为不可或缺的一部分,以各种形式和大小存在于城市的街头巷尾,商业中心和交通要道。广告牌是城市生命线组成的一部分。但是由于天气因素、材料老化、不当维…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

C++--string的模拟实现
一,引言 string的模拟实现是只对string对象中给的主要功能经行模拟实现,其目的是加强对string的底层了解,以便于在以后的学习或者工作中更加熟练的使用string。本文中的代码仅供参考并不唯一。 二,默认成员函数 string主要有三个成员变量,…...
