2023大联盟2比赛总结
比赛链接
反思
T1
奇怪的贪心和构造题一直是我的软肋部分
T2
简单题
T3
也不难
T4
套路没学过,感觉还是太菜了
题解
A
考虑先给图随便染色,然后调整
因为每个点的度数为 3 3 3,所以如果有 x → u → v x\to u\to v x→u→v 的颜色全部相同,那么修改 u u u 的颜色一定能使 u u u 符合条件,然后就用队列存储调整的点,一直调整即可
估算一下时间复杂度是 O ( n ) O(n) O(n) 级别的,肯定不会调整很多次
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
const int N=200100;
int col[N],deg[N];
bool inq[N];
vector<int> G[N];
queue<int> que;
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
void upd(int x){deg[x]=0;for(int v:G[x]) if(col[v]==col[x]) deg[x]++;if(deg[x]>=2&&!inq[x]) inq[x]=1,que.push(x);
}
void work(){int n=read(),m=read();while(!que.empty()) que.pop();for(int i=1;i<=n;i++) G[i].clear(),inq[i]=0;for(int i=1;i<=m;i++){int x=read(),y=read();G[x].pb(y),G[y].pb(x);}for(int i=1;i<=n;i++) col[i]=0;for(int i=1;i<=n;i++) upd(i);int cnt=0;while(!que.empty()){int u=que.front();que.pop();inq[u]=0;if(deg[u]<2) continue;cnt++;if(cnt>m) break;col[u]^=1;upd(u);for(int v:G[u]) upd(v);}if(!que.empty()) puts("GG");else{for(int i=1;i<=n;i++) printf("%d ",col[i]);puts("");return;}
}
int main(){freopen("classical.in","r",stdin);freopen("classical.out","w",stdout);int T=read();while(T--) work();fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}B
感觉这才是本场比赛的签到题
可以发现操作类似冒泡排序,然后手玩一下样例发现答案为逆序对数
无解情况判一下奇偶性即可
时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
#include <bits/stdc++.h>
#define lowbit(x) x&-x
using namespace std;
typedef long long LL;
typedef pair<int,int> pii;
const int N=1000100;
int n,p[N],tr[N],a[2][N],b[2][N];
pii pos[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
void add(int x){ for(;x<=n;x+=lowbit(x)) tr[x]++;}
int ask(int x){int res=0;for(;x;x-=lowbit(x)) res+=tr[x];return res;
}
int main(){freopen("rotate.in","r",stdin);freopen("rotate.out","w",stdout);n=read();for(int i=1;i<=n;i++) a[0][i]=read();for(int i=1;i<=n;i++) a[1][i]=read();for(int i=1;i<=n;i++) b[0][i]=read();for(int i=1;i<=n;i++) b[1][i]=read();for(int i=1;i<=n;i++) pos[b[0][i]]={0,i},pos[b[1][i]]={1,i};//check -1for(int i=1;i<=n;i++){int x=a[0][i];if(!pos[x].first&&pos[x].second==i) continue;if(((pos[x].first-i)&1)!=(pos[x].second&1)){ puts("-1");exit(0);}}for(int i=1;i<=n;i++) p[i]=pos[a[0][i]].second;LL ans=0;for(int i=n;i>=1;i--) ans+=ask(p[i]),add(p[i]);printf("%lld\n",ans);fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}C
这道题最重要的想法是:分治
考虑对于左上角 ( x 1 , y 1 ) (x_1,y_1) (x1,y1),右下角 ( x 2 , y 2 ) (x_2,y_2) (x2,y2) 的矩形求出覆盖矩形内所有 1 1 1 的方案数,这可以枚举行和列的分割线,递归下去求解
时间复杂度 O ( n 5 ) O(n^5) O(n5),需要加一些剪枝就能卡过去了
#include <bits/stdc++.h>
using namespace std;
bool Mbe;
const int N=65;
int n,s[N][N],f[N][N][N][N];
bool a[N][N];
char str[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
inline void chkmin(int &x,int y){ if(y<x) x=y;}
int calc(int lx,int ly,int rx,int ry){ return s[rx][ry]-s[lx-1][ry]-s[rx][ly-1]+s[lx-1][ly-1];}
int solve(int lx,int ly,int rx,int ry){auto &t=f[lx][ly][rx][ry];if(t!=-1) return t;if(!calc(lx,ly,rx,ry)){ t=0;return 0;}if(rx-lx+1<ry-ly+1){bool flg=1;for(int i=ly;i<=ry;i++) if(!calc(lx,i,rx,i)){ flg=0;break;}if(flg){ t=ry-ly+1;return t;}}else{bool flg=1;for(int i=lx;i<=rx;i++) if(!calc(i,ly,i,ry)){ flg=0;break;}if(flg){ t=rx-lx+1;return t;}}t=max(rx-lx+1,ry-ly+1);//枚举分割线for(int i=lx;i<rx;i++){int tmp=solve(lx,ly,i,ry);if(tmp<t) chkmin(t,tmp+solve(i+1,ly,rx,ry));}for(int j=ly;j<ry;j++){int tmp=solve(lx,ly,rx,j);if(tmp<t) chkmin(t,tmp+solve(lx,j+1,rx,ry));}return t;
}
bool Med;
int main(){freopen("detection.in","r",stdin);freopen("detection.out","w",stdout);// fprintf(stderr,"%.3lf MB\n",(&Mbe-&Med)/1048576.0);n=read();for(int i=1;i<=n;i++){scanf("%s",str+1);for(int j=1;j<=n;j++) a[i][j]=str[j]=='T';}for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];memset(f,-1,sizeof(f));printf("%d\n",solve(1,1,n,n));fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}D
感觉是套路题
首先 O ( n 2 ) O(n^2) O(n2) 的树形 d p dp dp 是好做的
考虑 k = 1 k=1 k=1 的部分分,这一部分有一个经典的想法:考虑答案即为 ∏ s i z 每一个联通快 \prod siz_{每一个联通快} ∏siz每一个联通快,直接做仍是 O ( n 2 ) O(n^2) O(n2) 的,重要:考虑它的组合意义,即为在每个连通块内选一个点的方案数,这个可以令 f i , 0 / 1 f_{i,0/1} fi,0/1 表示 i i i 所在的连通块是否选过点的方案和,时间复杂度 O ( n ) O(n) O(n),期望得分 50 p t s 50pts 50pts
考虑一步转化是: s k = ∑ i = 0 k { k i } s i ‾ = ∑ i = 0 k { k i } ( s i ) i ! s^k=\sum\limits_{i=0}^{k}{k\brace i}s^{\underline{i}}=\sum\limits_{i=0}^{k}{k\brace i}\binom{s}{i}i! sk=i=0∑k{ik}si=i=0∑k{ik}(is)i!
考虑 { k i } k\brace i {ik} 和 i ! i! i! 都是好算的,主要是 ( s i ) \binom{s}{i} (is),这个可以根据组合意义用 d p dp dp 计算,即令 f i , j f_{i,j} fi,j 为 i i i 的联通快内选 j j j 个点的方案和,但 j ≤ k j\le k j≤k,所以时间复杂度 O ( n k ) O(nk) O(nk)
#include <bits/stdc++.h>
using namespace std;
const int N=100100,K=110,P=1e9+7;
int n,m,fac[K],siz[N],t[K];
int e[N],ne[N],h[N],idx;
int stir2[K][K];
int f[N][K],g[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
void add(int x,int y){ e[idx]=y,ne[idx]=h[x],h[x]=idx++;}
void dfs(int u){f[u][0]=f[u][1]=1,siz[u]=1;for(int i=h[u];~i;i=ne[i]){int v=e[i];dfs(v);for(int j=0;j<=min(m,siz[u]+siz[v]);j++) t[j]=0;for(int j=0;j<=siz[u];j++) t[j]=1ll*f[u][j]*g[v]%P;// for(int j=0;j<=m;j++) cout<<t[j]<<' ';cout<<'\n';for(int j=0;j<=siz[u];j++) for(int k=0;k<=min(siz[v],m-j);k++)t[j+k]=(t[j+k]+1ll*f[u][j]*f[v][k])%P;siz[u]=min(m,siz[u]+siz[v]);for(int j=0;j<=siz[u];j++) f[u][j]=t[j];}for(int i=0;i<=m;i++) g[u]=(g[u]+1ll*stir2[m][i]*fac[i]%P*f[u][i])%P;
}
int main(){freopen("calc.in","r",stdin);freopen("calc.out","w",stdout);n=read(),m=read();stir2[0][0]=1;for(int i=1;i<=m;i++)for(int j=1;j<=i;j++) stir2[i][j]=(stir2[i-1][j-1]+1ll*j*stir2[i-1][j])%P;fac[0]=1;for(int i=1;i<=m;i++) fac[i]=1ll*fac[i-1]*i%P;memset(h,-1,sizeof(h));for(int i=2;i<=n;i++) add(read(),i);dfs(1);printf("%d\n",g[1]);fprintf(stderr,"%d ms\n",int(1e3*clock()/CLOCKS_PER_SEC));return 0;
}相关文章:

2023大联盟2比赛总结
比赛链接 反思 T1 奇怪的贪心和构造题一直是我的软肋部分 T2 简单题 T3 也不难 T4 套路没学过,感觉还是太菜了 题解 A 考虑先给图随便染色,然后调整 因为每个点的度数为 3 3 3,所以如果有 x → u → v x\to u\to v x→u→v 的颜…...
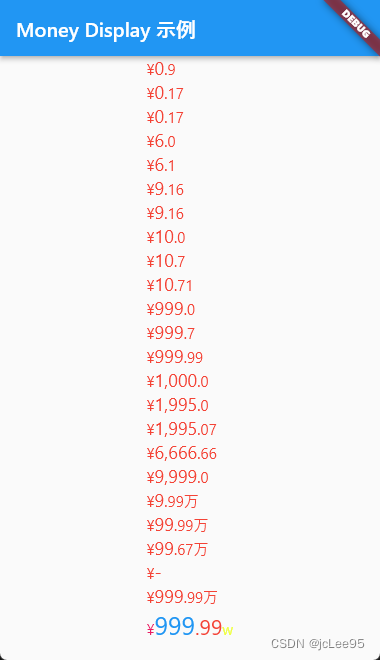
Flutter笔记:电商中文货币显示插件Money Display
Flutter笔记 电商中文货币显示插件 Money Display 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/1338…...
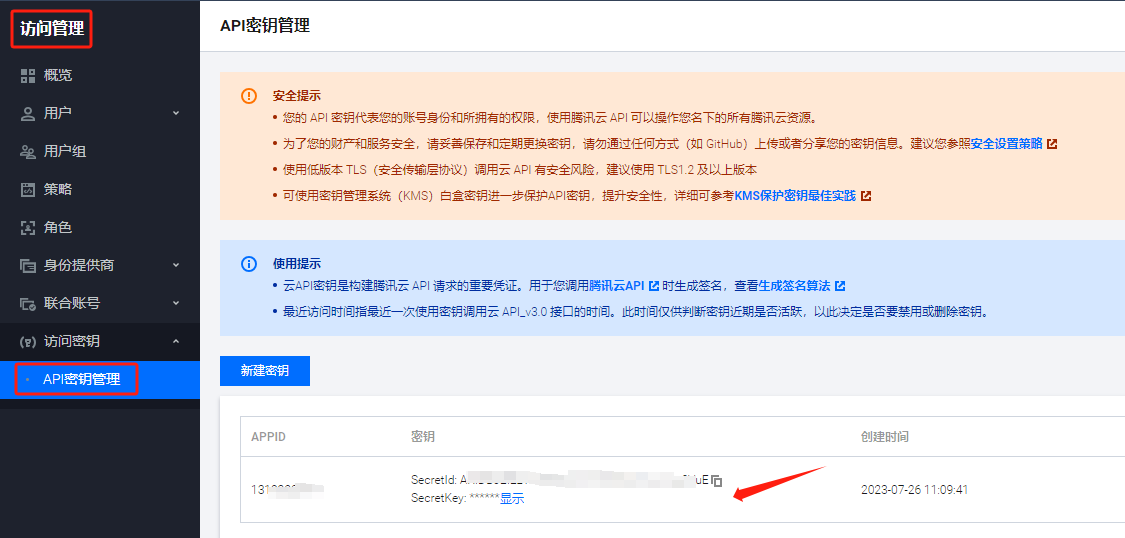
腾讯云上创建 对象存储cos
1. 登录腾讯云, 找到对象存储cos 2. 创建存储桶 3. 获取4个配置参数 桶名称 / 地域secretId / secretKey...
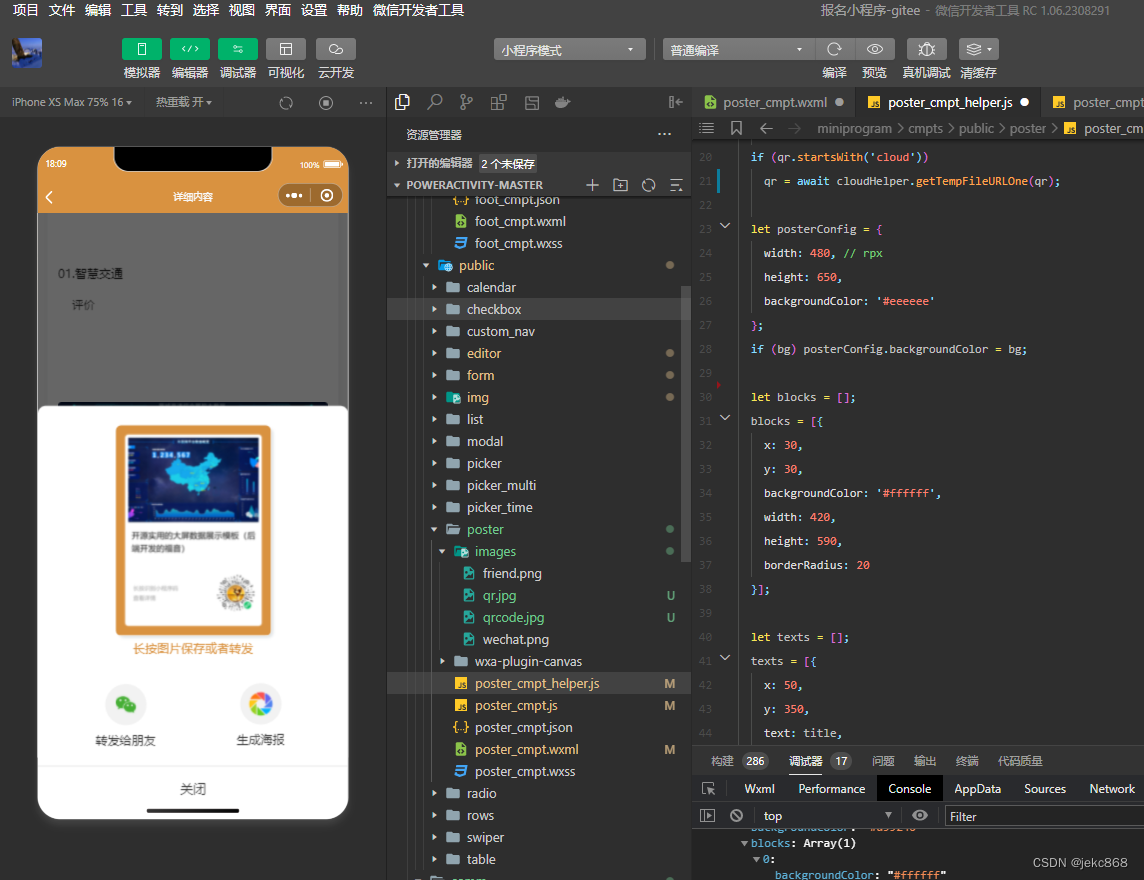
微信小程序生成海报
效果: js1: const cloudHelper = require(../../../helper/cloud_helper.js);async function config1({cover,title,desc,qr,bg = }) {var qr1 ="images/qr.png"var qr2 ="https://636c-cloud1-0gu29f2j63906b7e-1319556650.tcb.qcloud.la/activitycomm/setu…...
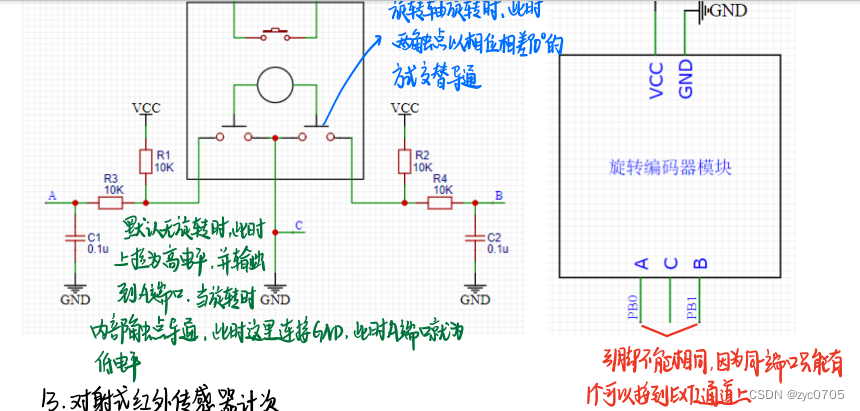
stm32学习笔记:EXIT中断
1、中断系统 中断系统是管理和执行中断的逻辑结构,外部中断是众多能产生中断的外设之一。 1.中断: 在主程序运行过程中,出现了特定的中断触发条件 (中断源,如对于外部中断来说可以是引脚发生了电平跳变,对于定时器来…...

css 块元素、行内元素、行内块元素相互转换
在HTML和CSS中,元素可以分为三类:块级元素(Block-level Elements)、内联元素(Inline Elements)和内联块级元素(Inline-block Elements)。 块级元素(Block-level Elements…...

【JUC】多线程基础概述
文章目录 1. 一锁二并三程2. 用户线程和守护线程 1. 一锁二并三程 一锁:synchronized 二并: 并发:一台处理器“同时”处理多个任务,同一时刻只有一个事件发生并行:多台处理器同时处理多个任务,同一时刻多个处理器分…...

Git 回退代码的两种方法对比
Git 回退代码版本 在项目的开发中,有时候还是会出现,一些误提交了一些代码,这时候就会想撤回提交的代码,在Git中有两种方法可以使用,现在通过对比方法比较这两种方法的区别,分别适用于哪些情况?…...
Avalonia常用小控件Charts
1.项目下载地址:https://gitee.com/confusedkitten/avalonia-demo 2.UI库Semi.Avalonia,项目地址 https://github.com/irihitech/Semi.Avalonia 3.Charts库,LiveChartsCore.SkiaSharpView.Avalonia,Nuget获取只有预览库&#x…...

【Hugging Face】管理 huggingface_hub 缓存系统
摘要 这篇文档介绍了Hugging Face Hub的缓存系统。该系统旨在提供一个中央缓存,以便不同版本的文件可以被下载和缓存。缓存系统将文件组织成模型、数据集和空间等不同的目录,每个目录包含特定类型的文件。系统确保如果文件已经下载并更新,除非明确要求,否则不会再次下载。…...

Python学习基础笔记六十六——对象的方法
我们已经学习到的对象类型: 整数类型的对象 字符串类型的对象 列表类型的对象 元组类型的对象 对象通常都有属于自己的方法(method) 调用对象的方法和调用函数差不多,只要在前面加上所属对象的一个点。 var1 [1, 2, 3,4, 5,…...

建立一个新的高阶数学教授模式,知其然,知其用,知其之所以然,知其所以然
1. 传统常用的模式 概念,性质,定理,定理证明,定理应用; 这个学习模式挺好的,但是定理证明过程往往很冗长,而且不易记忆,也就是说,即使推导了定理,初学者也记…...

AtCoder ABC324G 启发式合并
题意 传送门 AtCoder ABC324G Generate Arrays 题解 逆则操作顺序考虑,可以看作至多 n n n 个联通分量不断合并的过程,此时使用启发式合并,即规模较小的连通分量向规模较大的连通分量合并,以单个元素合并为基本运算࿰…...
SpringBootCMS漏洞复现分析
SpringBootCMS,极速开发,动态添加字段,自定义标签,动态创建数据库表并crud数据,数据库备份、还原,动态添加站点(多站点功能),一键生成模板代码,让您轻松打造自己的独立网站ÿ…...
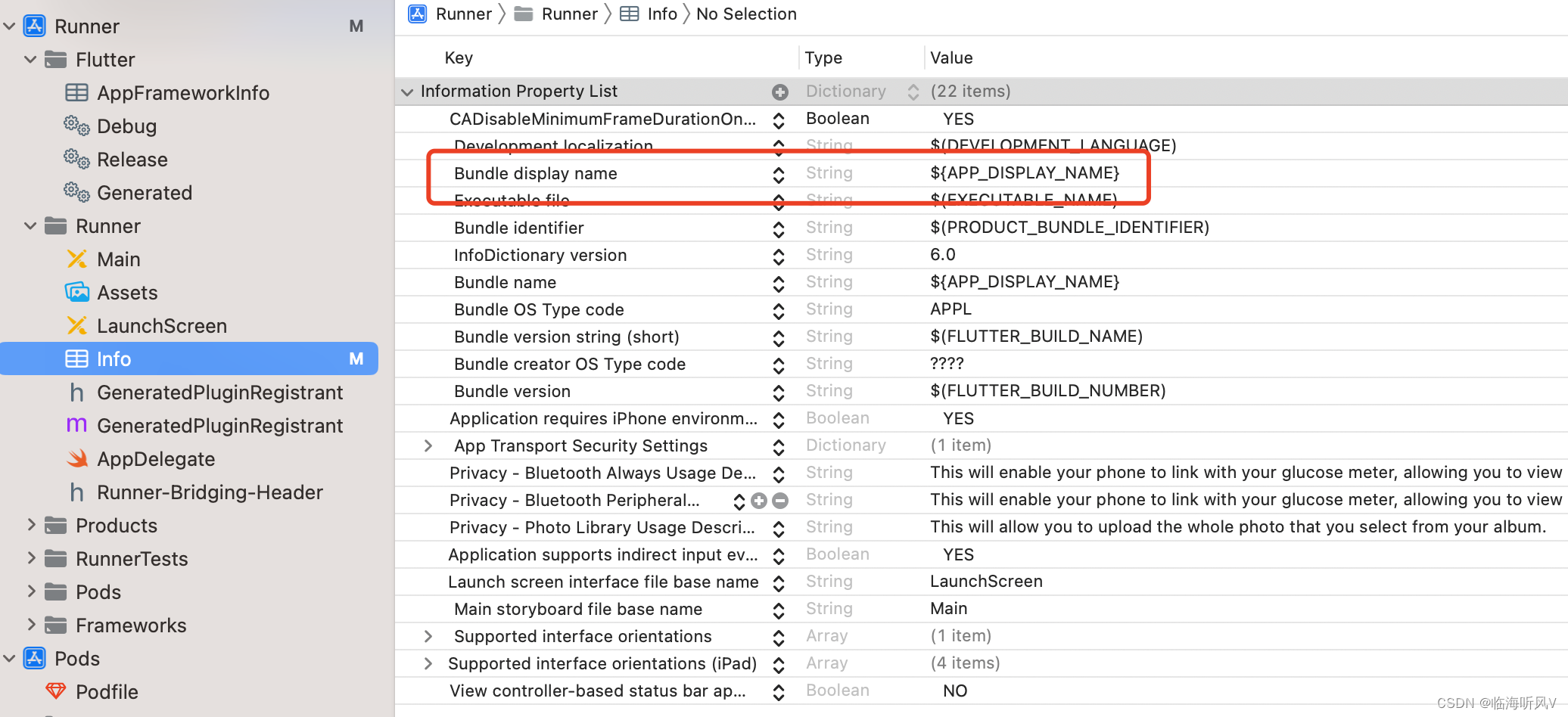
iOS- flutter flavor 多环境Configurations配置
一、点击PROJECT的Runner,选择Info选项,在Configurations下方的号添加不同环境的配置,如下图: 二、选择TAGETS的Runner项目,选择Build Settings选项,在输入框输入package,为不同环境配置相应的…...
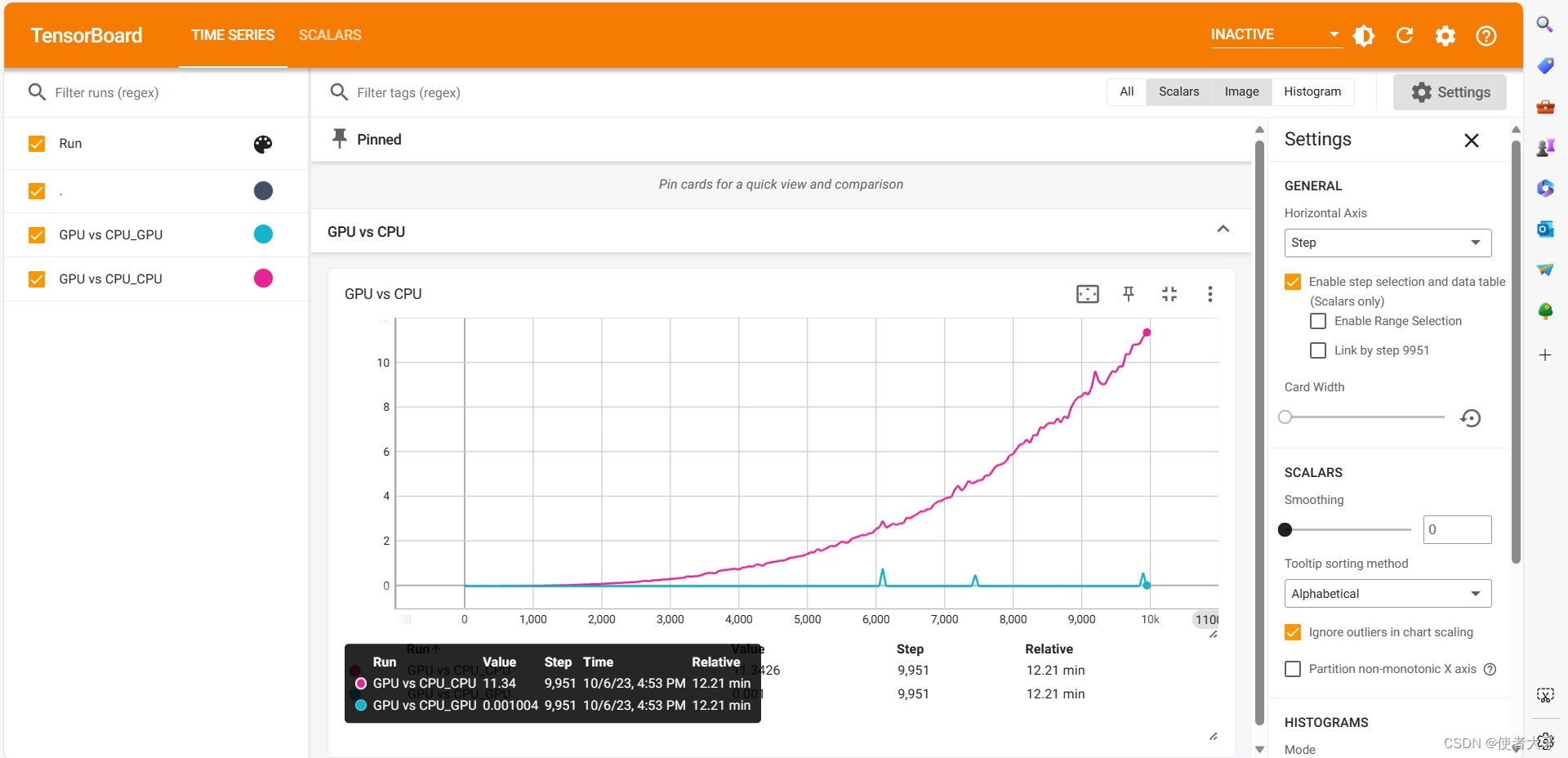
【PyTorchTensorBoard实战】GPU与CPU的计算速度对比(附代码)
0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解,但是内容可能存在不准确的地方。如果发现文中错误,希望批评指正,共同进步。 本文基于PyTorch通过tensor点积所需要的时…...

npm 常用指令总结
1. 初始化包 一个存放了代码的文件夹,如果里面有 package.json 文件,则可以把这个文件夹称之为包。 npm init -y 注意: 由于包名不能有中文,不能有大写,不能和未来要下载的包重名. 所以我们快速初始化包时,我们的文件夹也不能违反前面说的规则.(因为默认会将文件夹的名称,作…...

布朗大学发现GPT-4存在新问题,可通过非常见语言绕过限制
🦉 AI新闻 🚀 布朗大学发现GPT-4存在新漏洞,可通过非常见语言绕过限制 摘要:布朗大学计算机科学研究人员发现了OpenAI的GPT-4存在新漏洞,利用不太常见的语言如祖鲁语和盖尔语可以绕过各种限制。研究人员测试了GPT-4对…...

ESP32网络编程-TCP客户端数据传输
TCP客户端数据传输 文章目录 TCP客户端数据传输1、IP/TCP简单介绍2、软件准备3、硬件准备4、TCP客户端实现本文将详细介绍在Arduino开发环境中,实现一个ESP32 TCP客户端,从而达到与TCP服务器数据交换的目标。 1、IP/TCP简单介绍 Internet 协议(IP)是 Internet 的地址系统,…...

微信小程序入门级
目录 一.什么是小程序? 二.小程序可以干什么? 三.入门使用 3.1. 注册 3.2. 安装 3.3.创建项目 3.4.项目结构 3.5.应用 好啦今天就到这里了,希望能帮到你哦!!! 一.什么是小程序? 微信小程…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...
