当前位置： 首页 > news >正文

结构体对齐规则

news 2026/2/11 1:21:55

1.第一个成员在结构体变量偏移量为0的地址处。

2.其他成员变量对齐到某个数字(对齐数)的整数倍的地址处。(对齐数=编译器默认的一个对齐数与该成员大小的较小值）注意：目前有且只有VS编译器有默认为8.

3.结构体总大小为最大对齐数的整数倍。

4.如果嵌套了结构体，嵌套的结构体对齐到自己的最大对齐数整数倍处，结构体整体大小就是所有最大对齐数(含嵌套结构体对齐数)的整数倍。

例1：

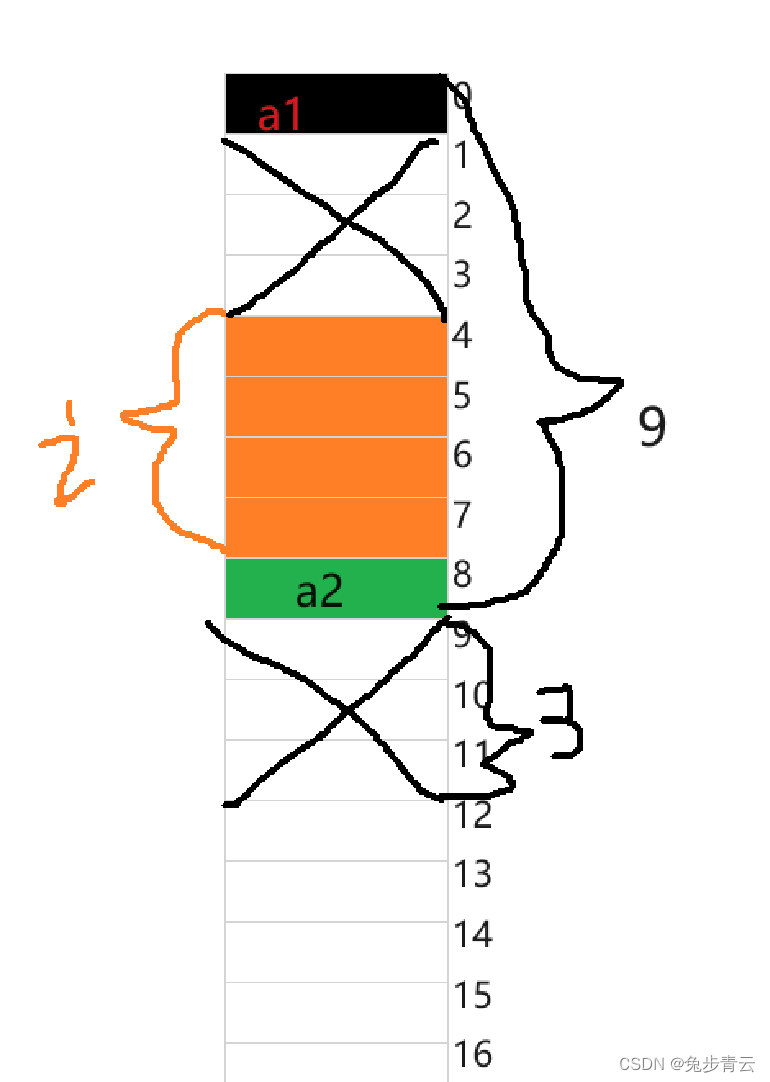
a1是char类型所以大小是1，i是int类型所以大小是4，a2是char类型所以大小是1，如上图所示，a1从0开始，占一个，因为1-3之间没有4的倍数所以i从4开始占4个空间大小，a2占一个(任何数都是1的倍数)；总共是9个空间的大小，因为9不是4的倍数，所以向后找直到所占大小是4的倍数浪费了3个空间大小，最终结果是12.

例2：

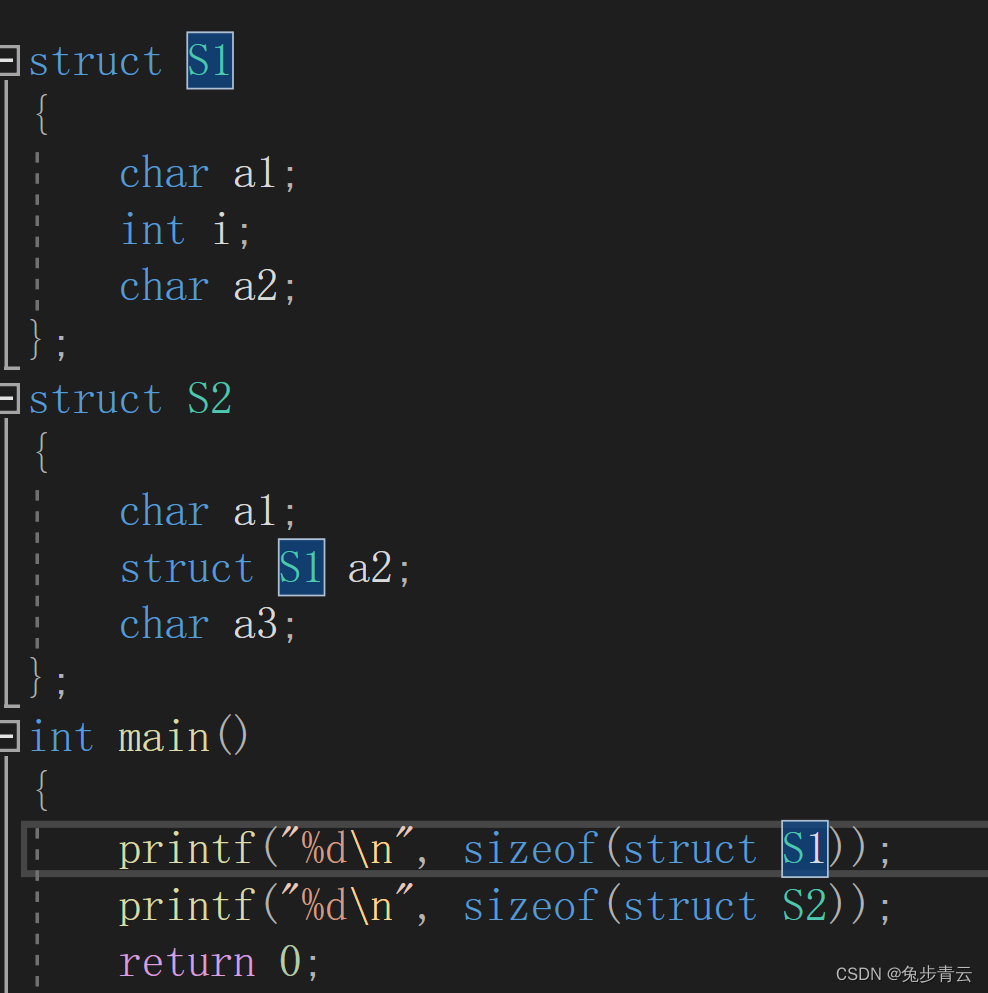
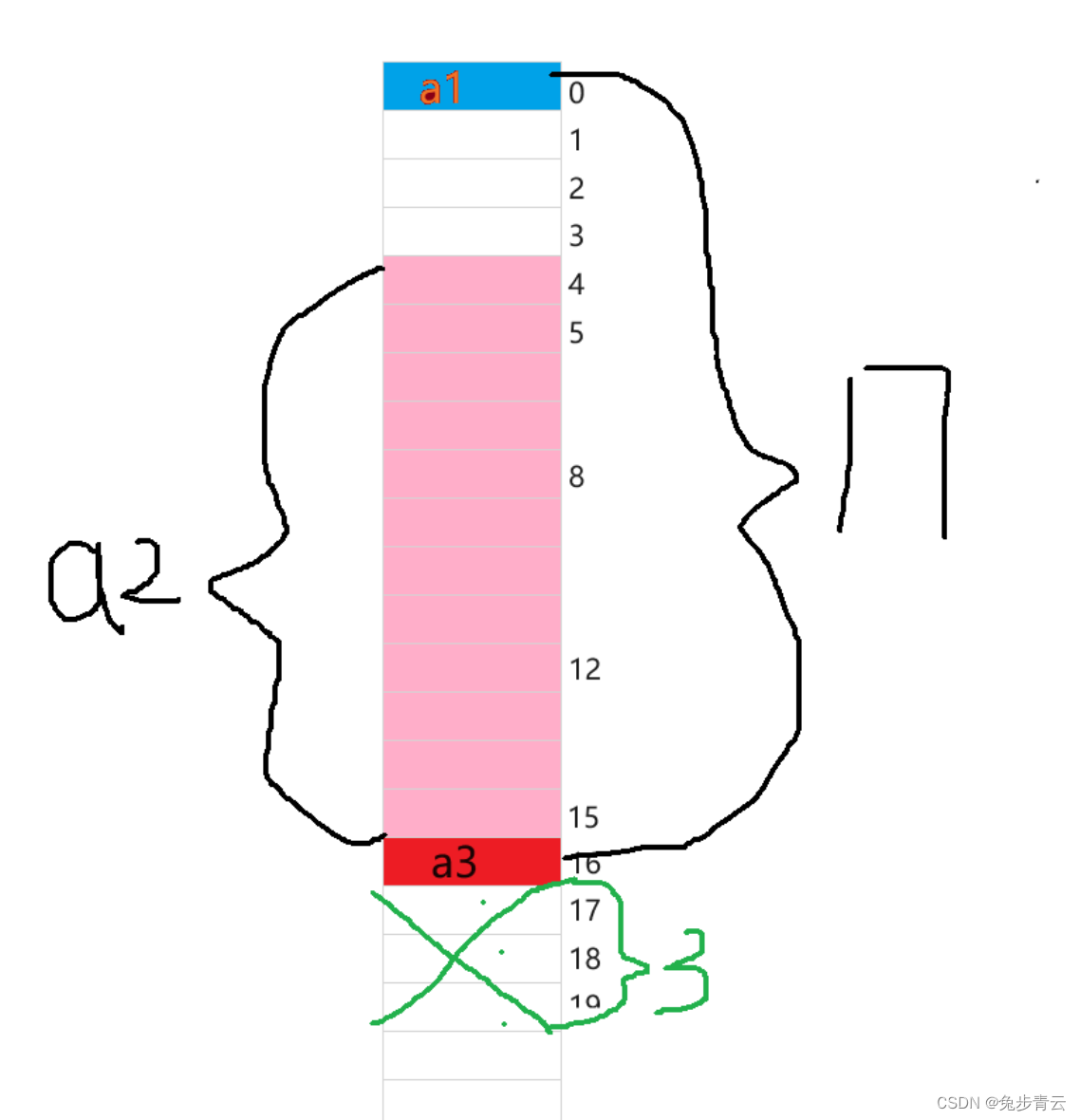
a1是char类型从0开始占一个，因为a2是嵌套的结构体所以对齐到自己的最大对齐数整数倍由上面例题可知是4，所以从4开始向后占12个空间大小(上面例题求出S1大小是12）,a3是char类型所以向后占一个空间的大小；上图可以看出0-16之间有17个数不是4的倍数，向后一直找直到为4的倍数，向后找3个总大小为20是4的倍数所以答案是20.

相关文章：

结构体对齐规则

1.第一个成员在结构体变量偏移量为0的地址处。 2.其他成员变量对齐到某个数字(对齐数)的整数倍的地址处。(对齐数编译器默认的一个对齐数与该成员大小的较小值）注意：目前有且只有VS编译器有默认为8. 3.结构体总大小为最大对齐数的整数倍。 4.如果嵌套…...

编程日记 2023/10/15 1:11:26

css 如何让元素内部文本和外部文本 一块显示省略号

实际上还是有这样的需求的 <div class"container"><span>啊啊啊啊啊啊啊啊</span>你好啊撒撒啊撒撒撒撒啊撒撒撒撒撒说</div>还是有这样的需求的哦。 div.container {width: 200px;white-space: nowrap;text-overflow: ellipsis;overflow:…...

编程日记 2023/10/15 1:10:25

SQL语句-中级

一、Mysql软件使用 1.启动/停止Mysql服务器 任务管理器 cmd命令&#xff1a;以管理员的身份打开cmd命令行 net start mysql80//开启net stop mysql80//停止 2.连接与断开Mysql服务器 注意要在bin目录下执行:-u用户名root&#xff0c;-p密码 mysql -u root -p 可能出现的…...

编程日记 2023/10/15 1:06:21

巧用h2-database.jar连接数据库

文章目录 一 、概述二、实践三、解决办法 一 、概述 H2 Database是一个开源的嵌入式数据库引擎&#xff0c;采用java语言编写&#xff0c;不受平台的限制&#xff0c;同时H2 Database提供了一个十分方便的web控制台用于操作和管理数据库内容。H2 Database还提供兼容模式&#…...

编程日记 2023/10/15 1:05:20

136.只出现一次的数字

136. 只出现一次的数字 - 力扣&#xff08;LeetCode&#xff09; 给你一个 非空 整数数组 nums &#xff0c;除了某个元素只出现一次以外&#xff0c;其余每个元素均出现两次。找出那个只出现了一次的元素。 你必须设计并实现线性时间复杂度的算法来解决此问题&#xff0c;且…...

编程日记 2023/10/15 1:03:18

mysql中遇到查询字段的别名与函数冲突问题

比如以下哎&#xff0c;我查询城市行业数量排名 select City, DENSE_RANK() over(ORDER BY COUNT(Id) DESC) rank, COUNT(Id) num,IndustrySubGroupName from base_companyinfo WHERE IndustrySubGroupName工业机器人 GROUP BY City 上面使用 DENSE_RANK() 函数来计算排名&am…...

编程日记 2023/10/15 1:01:16

直播获奖

题目描述 NOI2130 即将举行。为了增加观赏性&#xff0c; CCF 决定逐一评出每个选手的成 绩&#xff0c;并直播即时的获奖分数线。本次竞赛的获奖率为 &#x1d464;% &#xff0c;即当前排名前 &#x1d464;% 的选手的最低成绩就是即时的分数线。 更具体地&#xff0c…...

编程日记 2023/10/15 0:59:13

选择适合自身业务的HTTP代理有哪些因素决定？

相信对很多爬虫工作者和数据采集的企业来说&#xff0c;如何选购适合自己业务的HTTP代理是一个特别特别困扰的选题&#xff0c;市面上那么多HTTP代理厂商&#xff0c;好像这家有这些缺点&#xff0c;转头又看到另外一家的缺点&#xff0c;要找一家心仪的仿佛大海捞针。今天我们…...

编程日记 2023/10/15 0:58:11

1.3 do...while实现1+...100 for实现1+...100

思路&#xff1a;两个变量&#xff0c;一个变量存储数据之和&#xff0c;一个变量实现自增就行 do...while int i, s;i 1;s 0;do{s 1;i;} while (i < 100);cout << s << endl; for int i, j0;for (i 1; i < 100; i){j 1;}cout << j << …...

编程日记 2023/10/15 0:57:10

react数据管理之setState与Props

react数据管理之setState与Props setState调用原理 setState 是 React 中用于更新组件状态&#xff08;state&#xff09;的方法。它的调用原理可以分为以下几个步骤&#xff1a; 状态的改变&#xff1a;当调用 setState 时&#xff0c;React 会将新的状态对象与当前状态对象…...

编程日记 2023/10/15 0:56:09

如何保护我们的网络安全

保护网络安全是至关重要的&#xff0c;尤其是在今天的数字化时代。以下是一些保护网络安全的基本步骤&#xff1a; 1、使用强密码&#xff1a;使用包含字母、数字和特殊字符的复杂密码。不要在多个网站上重复使用相同的密码。定期更改密码。 2、启用双因素认证 (2FA)&#xff…...

编程日记 2023/10/15 0:55:07

springboot 制造装备物联及生产管理ERP系统

springboot 制造装备物联及生产管理ERP系统 liu1113625581...

编程日记 2023/10/15 0:54:06

Google zxing 生成带logo的二维码图片

环境准备 开发环境 JDK 1.8SpringBoot2.2.1Maven 3.2 开发工具 IntelliJ IDEAsmartGitNavicat15 添加maven配置 <dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.4.0</version> </…...

编程日记 2023/10/15 0:53:05

使用Python计算平面多边形间最短距离

要计算平面多边形间的最短距离&#xff0c;首先需要导入Excel表格中的多边形数据&#xff0c;然后使用GJK&#xff08;Gilbert-Johnson-Keerthi&#xff09;算法来判断两个多边形是否重叠。如果两个多边形不重叠&#xff0c;可以计算它们之间的最短距离。 以下是一个基本的Pyt…...

编程日记 2023/10/15 0:52:05

【Python】Python语言基础（中）

第十章 Python的数据类型 基本数据类型 数字 整数 整数就是整数 浮点数 在编程中&#xff0c;小数都称之为浮点数 浮点数的精度问题 print(0.1 0.2) --------------- 0.30000000000000004 ​​1.可以通过round()函数来控制小数点后位数 round(a b)&#xff0c;则表示…...

编程日记 2023/10/15 0:51:04

观察者模式、订阅者发布者模式、vtk中的观察者模式

文章目录 什么是观察者模式vtk是如何实现的观察者模式.AddObserver什么时候使用观察者模式&#xff1f;什么使用订阅发布者模式?观察者模式的实现订阅发布者的实现总结知识补充: 什么是观察者模式 用于在对象之间建立一对多的依赖关系&#xff0c;当一个对象的状态发生变化时…...

编程日记 2023/10/15 0:50:03

关于element-ui中，页面上有多个el-table并通过v-if、v-else等控制是否显示时，type=selection勾选框失效或不显示的问题

刚开始是勾选框那一列直接空了什么都不显示&#xff0c;搜索了一下说是给el-table标签增加id&#xff0c;加了之后是显示了&#xff0c;但是点击任何选框都会直接取消全部选中效果&#xff0c;翻了半天源码也没发现到底是哪里事件冲突了还是怎么回事&#xff0c;烦了&#xff0…...

编程日记 2023/10/15 0:48:59

Stewart六自由度正解、逆解计算-C#和Matlab程序

目录 一、Stewart并联六自由度正解计算 &#xff08;一&#xff09;概况 &#xff08;二&#xff09;Matlab正解计算 1、参考程序一 2、参考程序二 &#xff08;三&#xff09;C#程序正解计算 1、工程下载链接 2、正解运行计算 &#xff08;四&#xff09;正程…...

编程日记 2023/10/15 0:47:58

C语言 驼峰命名法和下划线命名法

在C语言中&#xff0c;变量命名遵循以下规则&#xff1a; 变量名只能由字母、数字和下划线组成。变量名必须以字母或下划线开头。变量名不能使用C语言中的关键字。变量名中不能出现连续的两个下划线。变量名区分大小写&#xff0c;例如&#xff0c;count和Count被视为两个不同…...

编程日记 2023/10/15 0:46:57

大数据学习(8)-hive压缩

&&大数据学习&& &#x1f525;系列专栏&#xff1a; &#x1f451;哲学语录: 承认自己的无知&#xff0c;乃是开启智慧的大门 &#x1f496;如果觉得博主的文章还不错的话&#xff0c;请点赞&#x1f44d;收藏⭐️留言&#x1f4dd;支持一下博>主哦&#x…...

编程日记 2023/10/15 0:44:55

网络六边形受到攻击

大家读完觉得有帮助记得关注和点赞&#xff01;&#xff01;&#xff01; 抽象 现代智能交通系统 &#xff08;ITS&#xff09; 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 &#xff08;…...

编程新知 2026/2/8 5:22:04

React 第五十五节 Router 中 useAsyncError的使用详解

前言 useAsyncError 是 React Router v6.4 引入的一个钩子&#xff0c;用于处理异步操作&#xff08;如数据加载&#xff09;中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误&#xff1a;捕获在 loader 或 action 中发生的异步错误替…...

编程新知 2025/11/25 10:36:53

论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）

HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...

编程新知 2026/2/9 0:12:12

DeepSeek 赋能智慧能源：微电网优化调度的智能革新路径

目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

编程新知 2025/11/20 2:48:44

日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする

日语学习-日语知识点小记-构建基础-JLPT-N4阶段（33）：にする 1、前言（1）情况说明（2）工程师的信仰2、知识点（1）　にする1，接续：名词＋にする2，接续：疑问词＋にする3，（A）は（B）にする。（2）復習：（1）复习句子（2）ために　＆　ように（３）そう（４）にする3、…...

编程新知 2025/11/20 7:52:01

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍，多层嵌套定位示例

文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解（初学者版） 1. static（默认值） 2. relative（相对定位） 3. absolute（绝对定位） 4. fixed（固定定位） 5. sticky（粘性定位） 三、定位元素的层级关系（z-i…...

编程新知 2026/2/9 1:38:05

css的定位（position）详解：相对定位 绝对定位 固定定位

在 CSS 中&#xff0c;元素的定位通过 position 属性控制&#xff0c;共有 5 种定位模式&#xff1a;static&#xff08;静态定位&#xff09;、relative&#xff08;相对定位&#xff09;、absolute&#xff08;绝对定位&#xff09;、fixed&#xff08;固定定位&#xff09;和…...

编程新知 2026/2/6 6:35:29

工业自动化时代的精准装配革新：迁移科技3D视觉系统如何重塑机器人定位装配

AI3D视觉的工业赋能者 迁移科技成立于2017年&#xff0c;作为行业领先的3D工业相机及视觉系统供应商&#xff0c;累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成&#xff0c;通过稳定、易用、高回报的AI3D视觉系统&#xff0c;为汽车、新能源、金属制造等行…...

编程新知 2025/11/25 4:59:47

Map相关知识

数据结构 二叉树 二叉树&#xff0c;顾名思义&#xff0c;每个节点最多有两个“叉”&#xff0c;也就是两个子节点&#xff0c;分别是左子 节点和右子节点。不过&#xff0c;二叉树并不要求每个节点都有两个子节点&#xff0c;有的节点只 有左子节点&#xff0c;有的节点只有…...

编程新知 2026/2/4 16:21:14

有限自动机到正规文法转换器v1.0

1 项目简介 这是一个功能强大的有限自动机&#xff08;Finite Automaton, FA&#xff09;到正规文法&#xff08;Regular Grammar&#xff09;转换器&#xff0c;它配备了一个直观且完整的图形用户界面&#xff0c;使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

编程新知 2026/1/31 13:13:32