Stewart六自由度正解、逆解计算-C#和Matlab程序
目录
一、Stewart并联六自由度正解计算
(一)概况
(二)Matlab正解计算
1、参考程序一
2、参考程序二
(三)C#程序正解计算
1、工程下载链接
2、正解运行计算
(四)正程序打包下载程序合集
二、逆解计算
(一)Matlab逆解计算
1、Matlab逆解计算程序一
2、Matlab逆解计算程序二
3、Matlab逆解计算程序三
(二)C#程序逆解计算
1、工程下载链接
2、逆解运行计算
(三)逆解程序打包下载程序合集
一、Stewart并联六自由度正解计算
(一)概况
Stewart平台,也称为六自由度并联机构,是一种具有六个自由度(三个平移自由度和三个旋转自由度)的机械结构。它由一个固定的底座和一个可移动的平台组成,通过六个连杆连接底座和平台。
要进行Stewart平台的正解计算,即已知各个连杆的长度和底座上的固定点坐标,求解平台上的移动点坐标。正解计算可以通过以下步骤完成:
1. 定义底座和平台的坐标系。选择一个适当的坐标系,并将底座和平台的坐标系与之关联。
2. 确定底座上的固定点坐标。假设底座上有六个固定点,分别记作P1, P2, P3, P4, P5, P6,并给出它们在底座坐标系中的坐标。
3. 确定各个连杆的长度。假设有六个连杆,分别记作L1, L2, L3, L4, L5, L6,并给出它们的长度。
4. 确定平台上的移动点坐标。假设平台上有一个移动点M,并给出它在平台坐标系中的坐标。
5. 利用三角关系计算各个连杆的角度。根据已知的底座固定点坐标、连杆长度和平台上的移动点坐标,可以使用三角关系计算出各个连杆的角度。
6. 利用旋转矩阵计算平台的位姿。根据各个连杆的角度,可以构建旋转矩阵,然后将平台上的移动点坐标转换到底座坐标系中,从而得到平台的位姿。
以上步骤仅为大致的计算过程,具体实现时需要根据具体的连杆结构和坐标系选择进行适当的数学推导和计算。在实际应用中,还需要考虑误差校正、奇异姿态等问题。
请注意,Stewart平台的正解计算相对复杂,需要较强的数学和几何知识。如果你需要更详细和精确的计算结果,建议参考相关的文献或专业机器人学教材,或者使用专门的机器人仿真软件进行计算和分析。
(二)Matlab正解计算
1、参考程序一
以下是一个使用MATLAB编写的Stewart并联六自由度正解计算的示例程序:
%这个程序计算了Stewart并联六自由度的正解,其中腿的长度 L 和腿的旋转角度 theta 是输入参数。
%程序通过循环计算每个腿的末端点坐标,并使用这些坐标计算平台的旋转矩阵。
%最后,程序打印出腿的末端点坐标和平台的旋转矩阵。
%你可以根据需要修改腿的长度和旋转角度,然后运行程序,即可得到相应的结果。% 输入参数
L = [1, 1, 1, 1, 1, 1]; % 腿的长度
theta = [0, 0, 0, 0, 0, 0]; % 腿的旋转角度(单位:弧度)% 计算腿的末端点坐标
P = zeros(3, 6); % 存储末端点坐标
for i = 1:6P(:, i) = [L(i)*cos(theta(i)); L(i)*sin(theta(i)); 0];
end% 计算平台的旋转矩阵
R = zeros(3, 3); % 存储旋转矩阵
for i = 1:6R = R + cos(theta(i))*eye(3) + (1 - cos(theta(i)))*(P(:, i)*P(:, i)') - sin(theta(i))*skewSymmetricMatrix(P(:, i));
end% 打印结果
disp("腿的末端点坐标:");
disp(P);
disp("平台的旋转矩阵:");
disp(R);% 辅助函数:计算叉乘矩阵
function M = skewSymmetricMatrix(v)M = [ 0 -v(3) v(2);v(3) 0 -v(1);-v(2) v(1) 0 ];
end计算结果

2、参考程序二
% 输入参数
L = [0.5, 0.5, 0.5, 0.5, 0.5, 0.5]; % 腿的长度
theta = [pi/6, pi/4, pi/3, pi/6, pi/4, pi/3]; % 腿的旋转角度% 计算腿的末端点坐标
P = zeros(3, 6); % 存储末端点坐标
for i = 1:6P(:, i) = [L(i)*cos(theta(i)); L(i)*sin(theta(i)); 0];
end% 计算平台的旋转矩阵
R = zeros(3, 3); % 存储旋转矩阵
for i = 1:6R = R + cos(theta(i))*eye(3) + (1 - cos(theta(i)))*(P(:, i)*P(:, i)') - sin(theta(i))*skewSymmetricMatrix(P(:, i));
end% 打印结果
disp("腿的末端点坐标:");
disp(P);
disp("平台的旋转矩阵:");
disp(R);% 绘制图形
figure;
hold on;
grid on;
axis equal;
xlabel('X');
ylabel('Y');
zlabel('Z');% 绘制腿的末端点
scatter3(P(1,:), P(2,:), P(3,:), 'filled');% 绘制平台
platform = [0, 1, 1, 0, 0; 0, 0, 1, 1, 0; 0, 0, 0, 0, 0];
platform = R * platform;
patch(platform(1,:), platform(2,:), platform(3,:), 'r');% 绘制连线
for i = 1:6line([0, P(1,i)], [0, P(2,i)], [0, P(3,i)], 'Color', 'b');
end% 辅助函数:计算叉乘矩阵
function M = skewSymmetricMatrix(v)M = [ 0 -v(3) v(2);v(3) 0 -v(1);-v(2) v(1) 0 ];
end计算结果

(三)C#程序正解计算
1、工程下载链接
工程下载链接:
https://download.csdn.net/download/panjinliang066333/88421740
2、正解运行计算
给定下平台顶点坐标、六个连杆长度和角度,去计算旋转矩阵和位置矩阵。
以下是一个使用C#编写的Stewart并联六自由度正解计算的示例程序:
主运行程序

运行结果

在上述示例程序中,我们定义了底座上的固定点坐标、连杆长度和平台上的移动点坐标,并调用`StewartForwardKinematics`方法计算平台的位置坐标和姿态(旋转矩阵)。最后,我们将结果显示在控制台中。
请注意,这只是一个简化的示例程序,仅用于演示Stewart并联六自由度正解计算的基本思路。在实际应用中,可能需要考虑更多的细节和特殊情况,例如奇异姿态、误差校正等。如果需要更精确和完整的计算,建议参考相关的机器人学文献或专业软件。
(四)正程序打包下载程序合集
下载链接:
https://download.csdn.net/download/panjinliang066333/88421740
二、逆解计算
Stewart平台的逆解计算是指根据给定的目标位置和姿态,求解平台上各个执行器的长度和角度。逆解计算可以使用数值方法或解析方法进行。
(一)Matlab逆解计算
1、Matlab逆解计算程序一
%逆解计算L1=0.5;
L2=0.5;
L3=0.5;
L4=0.5;
L5=0.5;
L6=0.5;R11=4.3322;
R12=0.2105;
R13=-1.5;
R21=0.2105;
R22=4.4237;
R23=1.366;
R31=1.5;
R32=-1.36;
R33=4.1463;P1=[0.433;0.25;0];
P2=[0.3536;0.3536;0];
P3=[0.2500;0.4330;0];
P4=[0.433;0.25;0];
P5=[0.3536;0.3536;0];
P6=[0.2500;0.4330;0];
% 输入参数
L = [L1, L2, L3, L4, L5, L6]; % 腿的长度
R = [R11, R12, R13; R21, R22, R23; R31, R32, R33]; % 平台的旋转矩阵
P = [P1, P2, P3, P4, P5, P6]; % 腿的末端点坐标% 计算基座坐标系到平台坐标系的转换矩阵
T = [R, zeros(3,1); 0 0 0 1];% 计算腿的旋转角度
theta = zeros(1, 6); % 存储腿的旋转角度
for i = 1:6% 计算腿的末端点在基座坐标系下的坐标P_base = T \ [P(:, i); 1];P_base = P_base(1:3);% 计算腿的旋转轴a = L(i) * R(:, 3);% 计算腿的末端点在基座坐标系下在旋转轴方向上的投影b = dot(P_base, a) * a;% 计算腿的末端点在基座坐标系下在旋转轴垂直方向上的投影c = P_base - b;% 计算腿的旋转角度theta(i) = atan2(norm(cross(a, c)), dot(a, c));
end% 打印结果
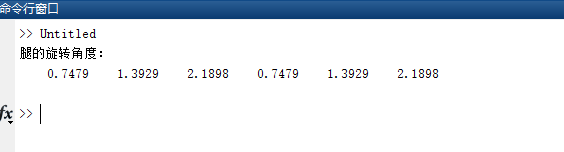
disp("腿的旋转角度:");
disp(theta);% 辅助函数:计算叉乘矩阵
function M = skewSymmetricMatrix(v)M = [ 0 -v(3) v(2);v(3) 0 -v(1);-v(2) v(1) 0 ];
end在程序中,你需要提供腿的长度 L、平台的旋转矩阵 R 和腿的末端点坐标 P。程序首先计算基座坐标系到平台坐标系的转换矩阵 T,然后根据逆运动学的原理,计算每个腿的旋转角度 theta。
计算过程中,程序首先将腿的末端点坐标转换到基座坐标系下,然后计算腿的旋转轴和末端点在旋转轴方向上的投影。最后,根据旋转轴和投影的关系,计算腿的旋转角度。
请注意,这只是一个简单的示例程序,具体的实现可能会根据你的具体需求和机构的几何结构而有所不同。你可能需要根据你的应用场景进行适当的修改和扩展。
运行结果
2、Matlab逆解计算程序二
%逆解计算R11=4.3322;
R12=0.2105;
R13=-1.5;
R21=0.2105;
R22=4.4237;
R23=1.366;
R31=1.5;
R32=-1.36;
R33=4.1463;P1=[0.433;0.25;0];
P2=[0.3536;0.3536;0];
P3=[0.2500;0.4330;0];
P4=[0.433;0.25;0];
P5=[0.3536;0.3536;0];
P6=[0.2500;0.4330;0];
% 输入参数
R = [R11, R12, R13; R21, R22, R23; R31, R32, R33]; % 平台的旋转矩阵
P = [P1, P2, P3, P4, P5, P6]; % 腿的末端点坐标% 计算腿的长度
L = zeros(1, 6); % 存储腿的长度
for i = 1:6fprintf("计算第 %d 条腿的长度:\n", i);% 步骤1: 计算 a_ia = R(:, 3);fprintf("步骤1: a_%d = R(:, 3) =\n", i);disp(a);% 步骤2: 计算 b_ib = P(:, i);fprintf("步骤2: b_%d = P%d =\n", i, i);disp(b);% 步骤3: 计算 L_iL(i) = norm(b - a);fprintf("步骤3: L_%d = norm(b_%d - a_%d) = %.4f\n", i, i, i, L(i));fprintf("\n");
end% 打印结果
disp("腿的长度:");
disp(L);在程序中,你需要提供腿的长度 L、平台的旋转矩阵 R 和腿的末端点坐标 P。程序会按照步骤计算每个腿的长度,并给出每个步骤的中间结果。
请注意,这只是一个示例程序,具体的实现可能会根据你的具体需求和机构的几何结构而有所不同。你可以根据需要修改程序,添加额外的计算步骤或输出结果。
计算结果

3、Matlab逆解计算程序三
%逆解计算R11=4.3322;
R12=0.2105;
R13=-1.5;
R21=0.2105;
R22=4.4237;
R23=1.366;
R31=1.5;
R32=-1.36;
R33=4.1463;P1=[0.433;0.25;0];
P2=[0.3536;0.3536;0];
P3=[0.2500;0.4330;0];
P4=[0.433;0.25;0];
P5=[0.3536;0.3536;0];
P6=[0.2500;0.4330;0];
% 输入参数
R = [R11, R12, R13; R21, R22, R23; R31, R32, R33]; % 平台的旋转矩阵
P = [P1, P2, P3, P4, P5, P6]; % 腿的末端点坐标% 计算腿的长度
L = zeros(1, 6); % 存储腿的长度
for i = 1:6fprintf("计算第 %d 条腿的长度:\n", i);% 步骤1: 计算 a_ia = R(:, 3);fprintf("步骤1: a_%d = R(:, 3) =\n", i);disp(a);% 步骤2: 计算 b_ib = P(:, i);fprintf("步骤2: b_%d = P%d =\n", i, i);disp(b);% 步骤3: 计算 L_iL(i) = norm(b - a);fprintf("步骤3: L_%d = norm(b_%d - a_%d) = %.4f\n", i, i, i, L(i));fprintf("\n");
end% 打印结果
disp("腿的长度:");
disp(L);在程序中,你需要提供腿的长度 L、平台的旋转矩阵 R 和腿的末端点坐标 P。程序会按照步骤计算每个腿的角度和长度,并给出每个步骤的中间结果。
请注意,这只是一个示例程序,具体的实现可能会根据你的具体需求和机构的几何结构而有所不同。你可以根据需要修改程序,添加额外的计算步骤或输出结果。
程序运行过程
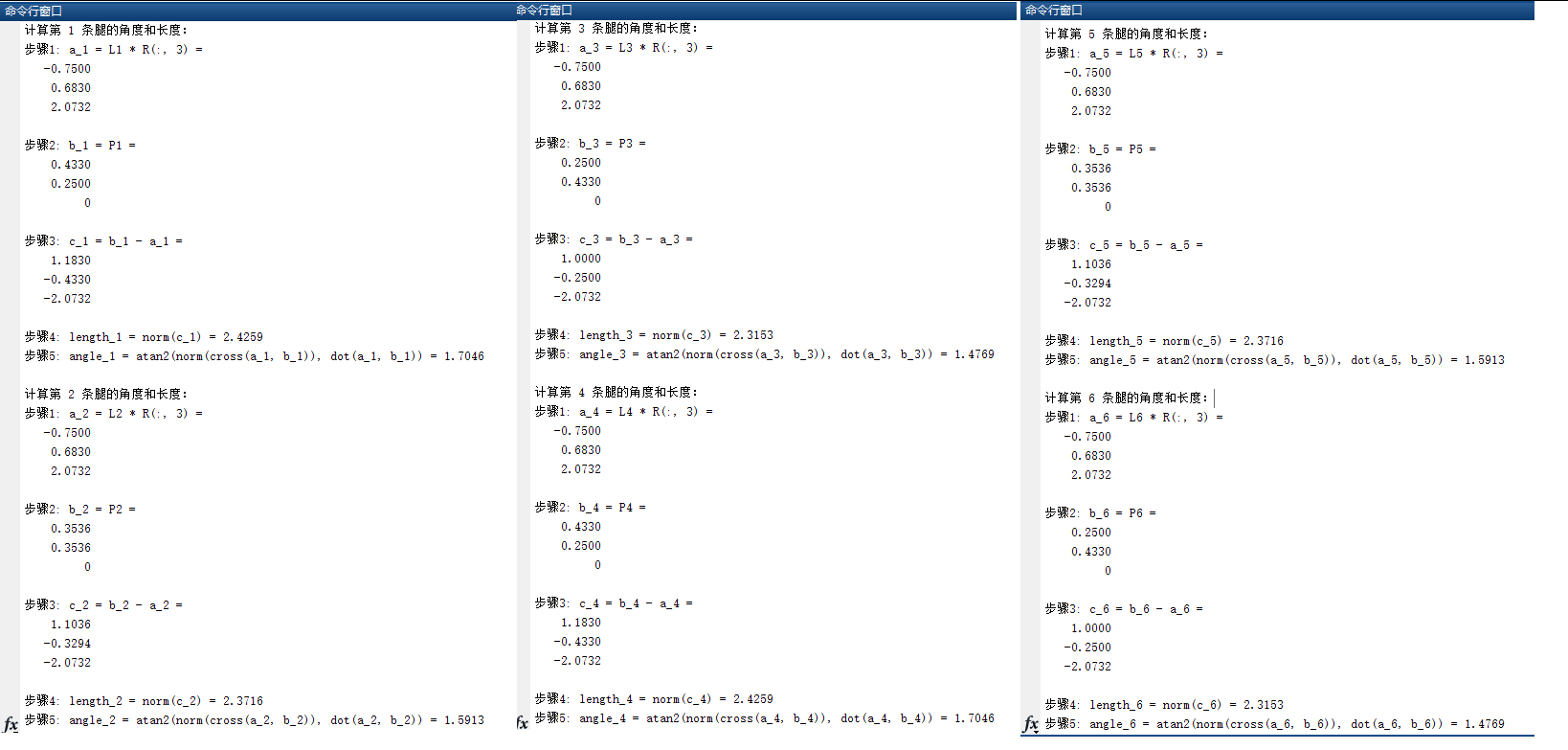
结果

(二)C#程序逆解计算
1、工程下载链接
工程下载链接:
https://download.csdn.net/download/panjinliang066333/88422020
2、逆解运行计算
给定下平台顶点坐标、六个连杆长度和角度,去计算旋转矩阵和位置矩阵。
以下是一个使用C#编写的Stewart并联六自由度正解计算的示例程序:
主运行程序

程序运行结果

(三)逆解程序打包下载程序合集
下载链接:
https://download.csdn.net/download/panjinliang066333/88422020
相关文章:

Stewart六自由度正解、逆解计算-C#和Matlab程序
目录 一、Stewart并联六自由度正解计算 (一)概况 (二)Matlab正解计算 1、参考程序一 2、参考程序二 (三)C#程序正解计算 1、工程下载链接 2、正解运行计算 (四)正程…...

C语言 驼峰命名法和下划线命名法
在C语言中,变量命名遵循以下规则: 变量名只能由字母、数字和下划线组成。变量名必须以字母或下划线开头。变量名不能使用C语言中的关键字。变量名中不能出现连续的两个下划线。变量名区分大小写,例如,count和Count被视为两个不同…...
-hive压缩)
大数据学习(8)-hive压缩
&&大数据学习&& 🔥系列专栏: 👑哲学语录: 承认自己的无知,乃是开启智慧的大门 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言📝支持一下博>主哦&#x…...
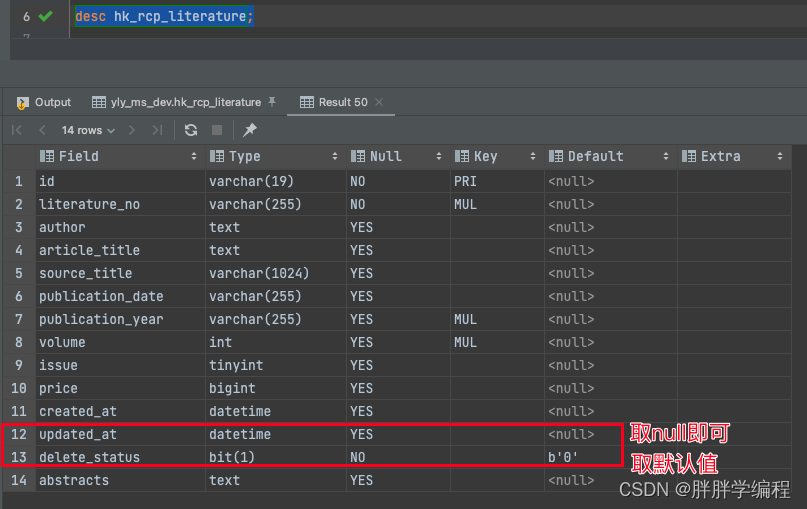
[sqoop]hive导入mysql,其中mysql的列存在默认值列
一、思路 直接在hive表中去掉有默认值的了列,在sqoop导入时,指定非默认值列即可, 二、具体 mysql的表 hive的表 create table dwd.dwd_hk_rcp_literature(id string,literature_no string,authors string,article_title string,source_title string…...
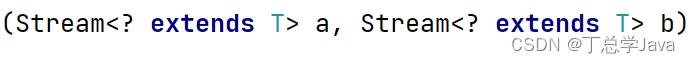
Stream流中的常用方法(forEach,filter,map,count,limit,skip,concat)和Stream流的特点
1、forEach方法 该方法接收一个Consumer接口是一个 消费型 的函数式接口,可以传递Lambda表达式,消费数据用来遍历流中的数据,是一个 终结 方法,遍历 之后就不能继续调用Stream流中的其他方法 package com.csdn.stream; import jav…...

2023大联盟2比赛总结
比赛链接 反思 T1 奇怪的贪心和构造题一直是我的软肋部分 T2 简单题 T3 也不难 T4 套路没学过,感觉还是太菜了 题解 A 考虑先给图随便染色,然后调整 因为每个点的度数为 3 3 3,所以如果有 x → u → v x\to u\to v x→u→v 的颜…...
Flutter笔记:电商中文货币显示插件Money Display
Flutter笔记 电商中文货币显示插件 Money Display 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/1338…...
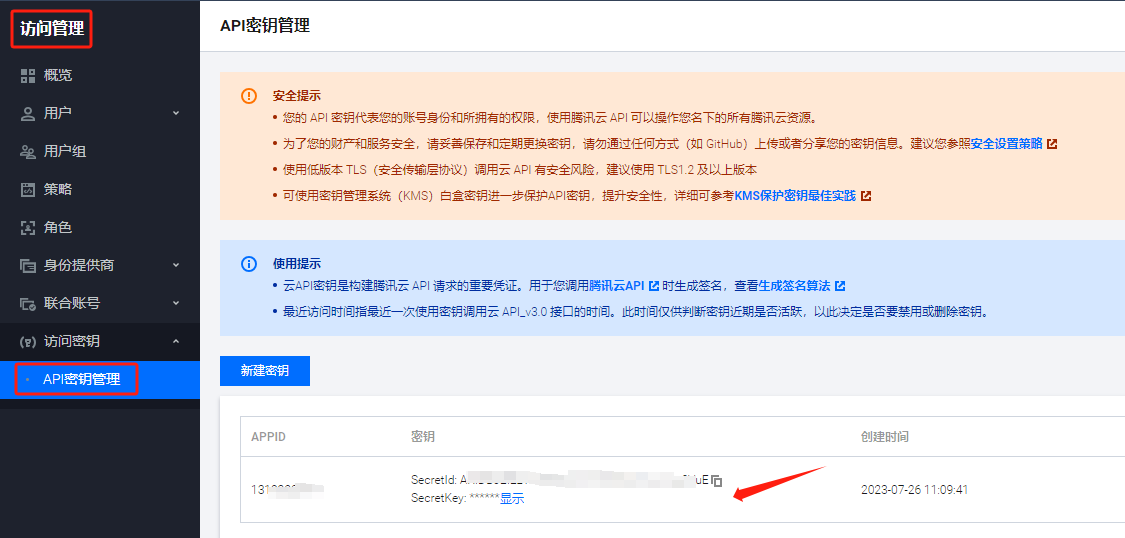
腾讯云上创建 对象存储cos
1. 登录腾讯云, 找到对象存储cos 2. 创建存储桶 3. 获取4个配置参数 桶名称 / 地域secretId / secretKey...
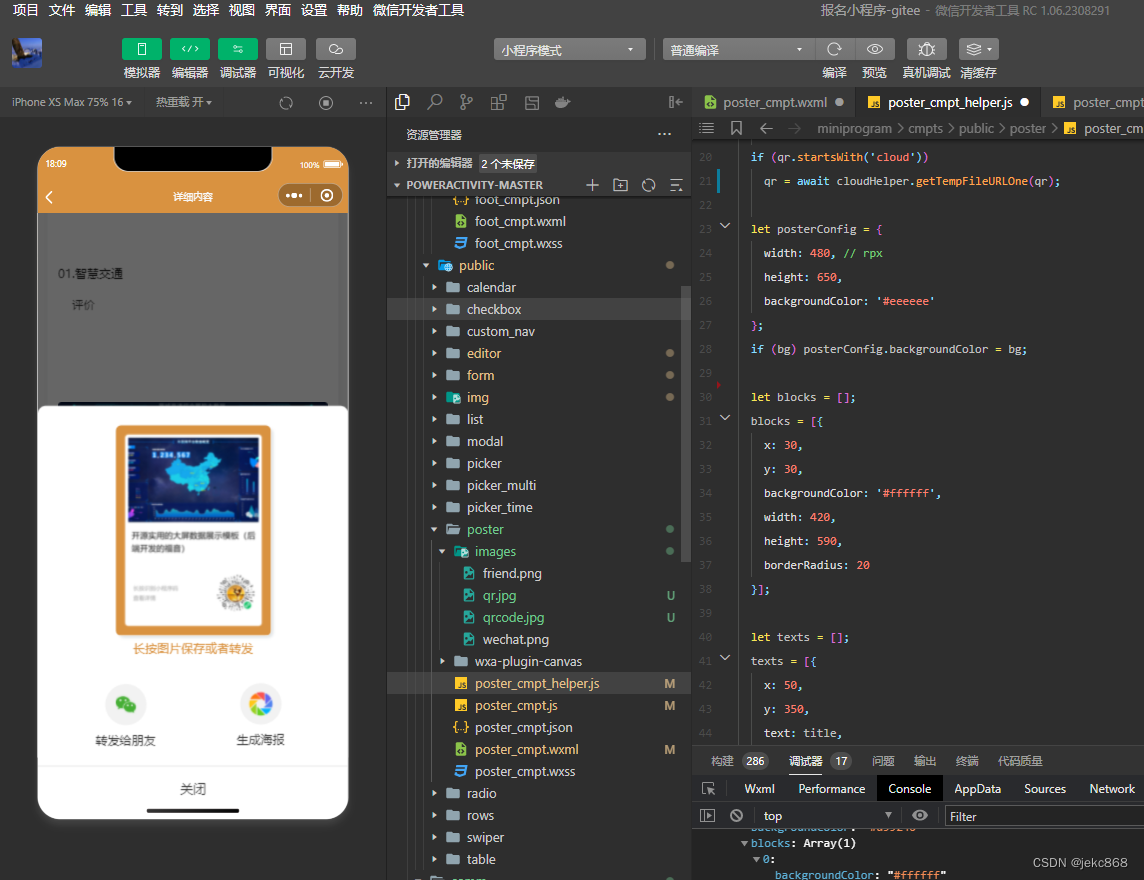
微信小程序生成海报
效果: js1: const cloudHelper = require(../../../helper/cloud_helper.js);async function config1({cover,title,desc,qr,bg = }) {var qr1 ="images/qr.png"var qr2 ="https://636c-cloud1-0gu29f2j63906b7e-1319556650.tcb.qcloud.la/activitycomm/setu…...
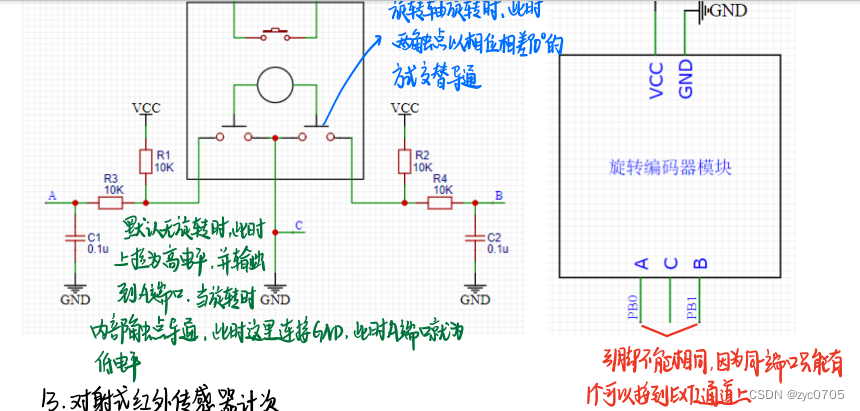
stm32学习笔记:EXIT中断
1、中断系统 中断系统是管理和执行中断的逻辑结构,外部中断是众多能产生中断的外设之一。 1.中断: 在主程序运行过程中,出现了特定的中断触发条件 (中断源,如对于外部中断来说可以是引脚发生了电平跳变,对于定时器来…...

css 块元素、行内元素、行内块元素相互转换
在HTML和CSS中,元素可以分为三类:块级元素(Block-level Elements)、内联元素(Inline Elements)和内联块级元素(Inline-block Elements)。 块级元素(Block-level Elements…...

【JUC】多线程基础概述
文章目录 1. 一锁二并三程2. 用户线程和守护线程 1. 一锁二并三程 一锁:synchronized 二并: 并发:一台处理器“同时”处理多个任务,同一时刻只有一个事件发生并行:多台处理器同时处理多个任务,同一时刻多个处理器分…...

Git 回退代码的两种方法对比
Git 回退代码版本 在项目的开发中,有时候还是会出现,一些误提交了一些代码,这时候就会想撤回提交的代码,在Git中有两种方法可以使用,现在通过对比方法比较这两种方法的区别,分别适用于哪些情况?…...
Avalonia常用小控件Charts
1.项目下载地址:https://gitee.com/confusedkitten/avalonia-demo 2.UI库Semi.Avalonia,项目地址 https://github.com/irihitech/Semi.Avalonia 3.Charts库,LiveChartsCore.SkiaSharpView.Avalonia,Nuget获取只有预览库&#x…...

【Hugging Face】管理 huggingface_hub 缓存系统
摘要 这篇文档介绍了Hugging Face Hub的缓存系统。该系统旨在提供一个中央缓存,以便不同版本的文件可以被下载和缓存。缓存系统将文件组织成模型、数据集和空间等不同的目录,每个目录包含特定类型的文件。系统确保如果文件已经下载并更新,除非明确要求,否则不会再次下载。…...

Python学习基础笔记六十六——对象的方法
我们已经学习到的对象类型: 整数类型的对象 字符串类型的对象 列表类型的对象 元组类型的对象 对象通常都有属于自己的方法(method) 调用对象的方法和调用函数差不多,只要在前面加上所属对象的一个点。 var1 [1, 2, 3,4, 5,…...

建立一个新的高阶数学教授模式,知其然,知其用,知其之所以然,知其所以然
1. 传统常用的模式 概念,性质,定理,定理证明,定理应用; 这个学习模式挺好的,但是定理证明过程往往很冗长,而且不易记忆,也就是说,即使推导了定理,初学者也记…...

AtCoder ABC324G 启发式合并
题意 传送门 AtCoder ABC324G Generate Arrays 题解 逆则操作顺序考虑,可以看作至多 n n n 个联通分量不断合并的过程,此时使用启发式合并,即规模较小的连通分量向规模较大的连通分量合并,以单个元素合并为基本运算࿰…...
SpringBootCMS漏洞复现分析
SpringBootCMS,极速开发,动态添加字段,自定义标签,动态创建数据库表并crud数据,数据库备份、还原,动态添加站点(多站点功能),一键生成模板代码,让您轻松打造自己的独立网站ÿ…...
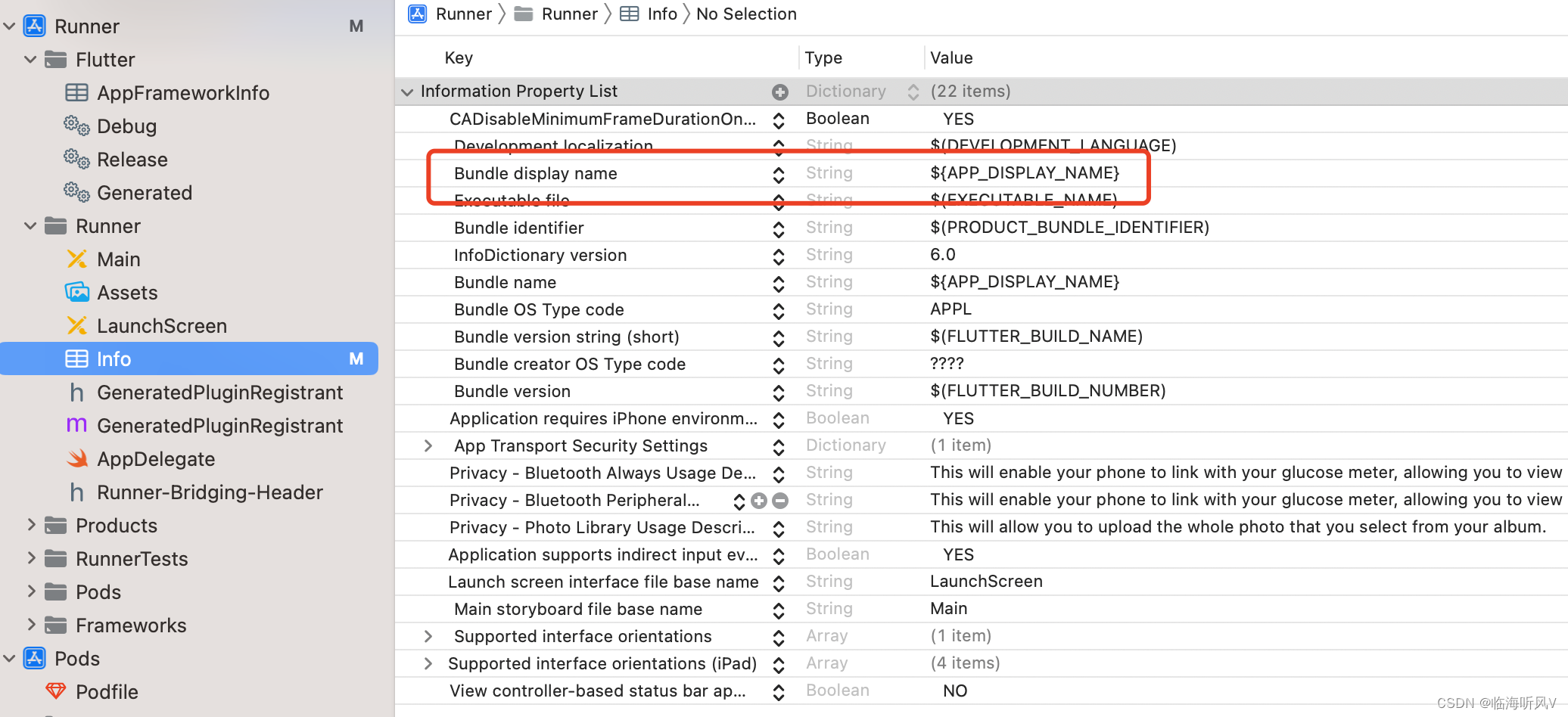
iOS- flutter flavor 多环境Configurations配置
一、点击PROJECT的Runner,选择Info选项,在Configurations下方的号添加不同环境的配置,如下图: 二、选择TAGETS的Runner项目,选择Build Settings选项,在输入框输入package,为不同环境配置相应的…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

python基础语法Ⅰ
python基础语法Ⅰ 常量和表达式变量是什么变量的语法1.定义变量使用变量 变量的类型1.整数2.浮点数(小数)3.字符串4.布尔5.其他 动态类型特征注释注释是什么注释的语法1.行注释2.文档字符串 注释的规范 常量和表达式 我们可以把python当作一个计算器,来进行一些算术…...
