9.Linear Maps
线性映射
线性映射是将向量作为输入并产生一些新向量作为输出的转换。
从坐标定义开始(数组),再到2,3,并展示它们是如何关联的
线性映射的坐标表示最终是矩阵,
1.坐标定义(数组)
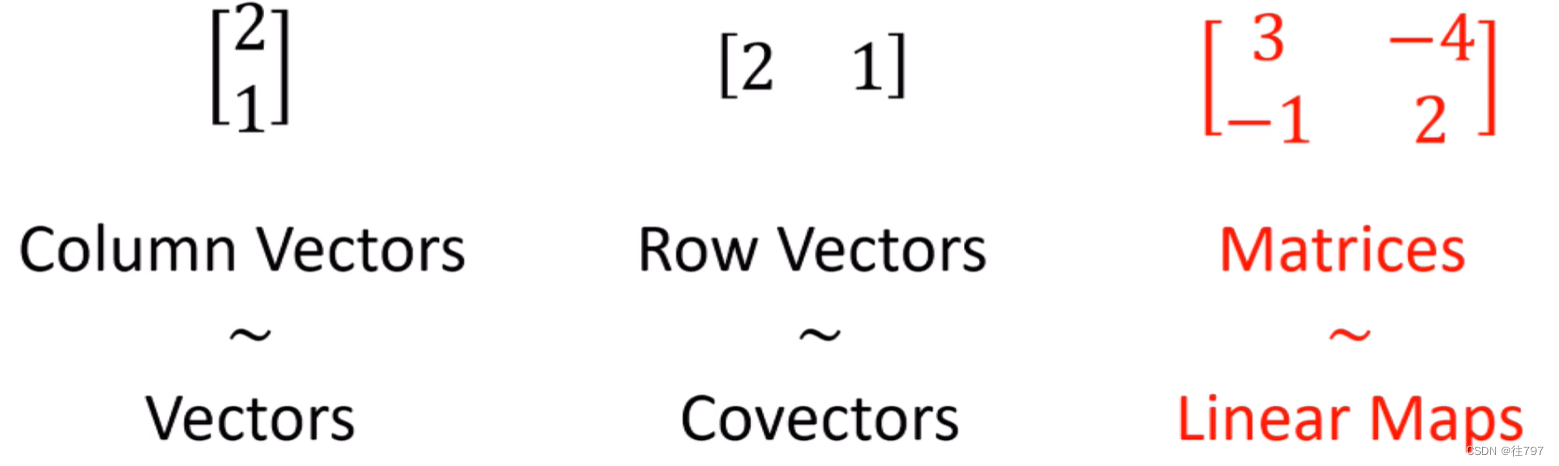
列向量是向量的坐标表示。
行向量是协向量的坐标表示。
矩阵是线性映射的坐标表示。
矩阵是如何转变向量的?
例子
现有一个作用于2x1列向量的2x2矩阵,输出的向量是?
但仅通过查看矩阵中的数字来理解矩阵在做什么会让人感到困惑。
但对所有这些数字的含义,有一个简单的解释:
注意,若使用列向量 作为输入,将得到矩阵的第一列作为输出。
若使用列向量 作为输入, 将得到矩阵的第二列作为输出。
现这些列向量 、
, 它们有点像基向量e1、e2的副本,
之所以说是像副本,是因为这里非常重要的一点:线性映射转换向量,但是线性映射不转换基向量!
因此,当使用线性映射转换向量时,基底是不会变的。 我们不会移动基底,


虽然输出向量可能与输入向量不同,但我们仍将使用相同的基底来测量输出向量,但话虽如此,对于矩阵,第 i 列会告诉你将第 i 个基向量的副本映射到哪里。
因此,从视觉上观察一下,
现有两基底:e1、e2,还有两向量v,w。v和w有点像e1、e2的副本,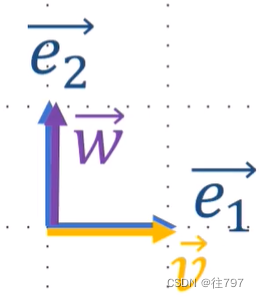
有个矩阵如下:
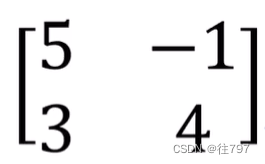
那么该矩阵会将向量v(v像e1的副本)发送到哪?
只看矩阵的第一列,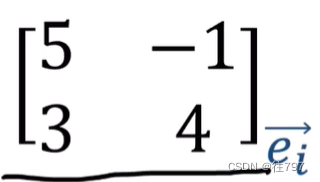
它表示向量5e1+3e2 , 这就是线性映射的输出,![]()
V在视觉上:
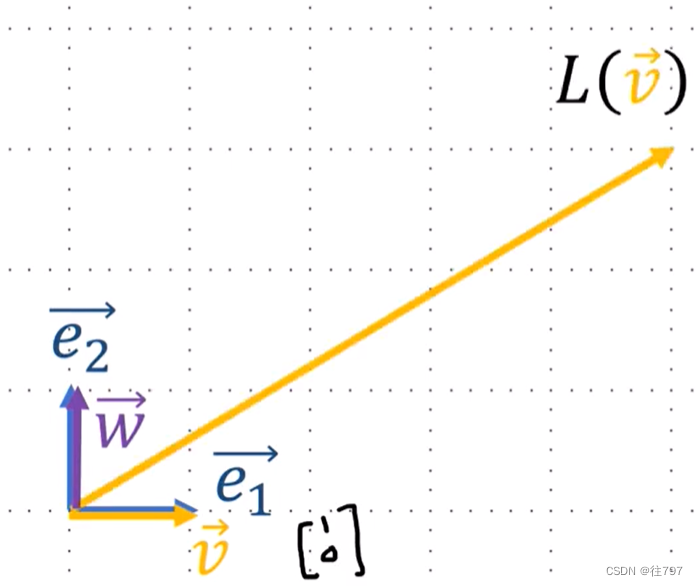
矩阵对向量w(e2的副本)做了什么?
看矩阵的第二列,给我们输出 -e1+4e2
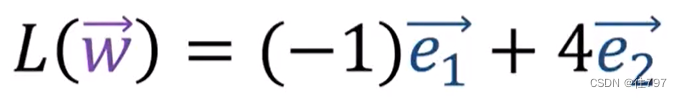
视觉上:
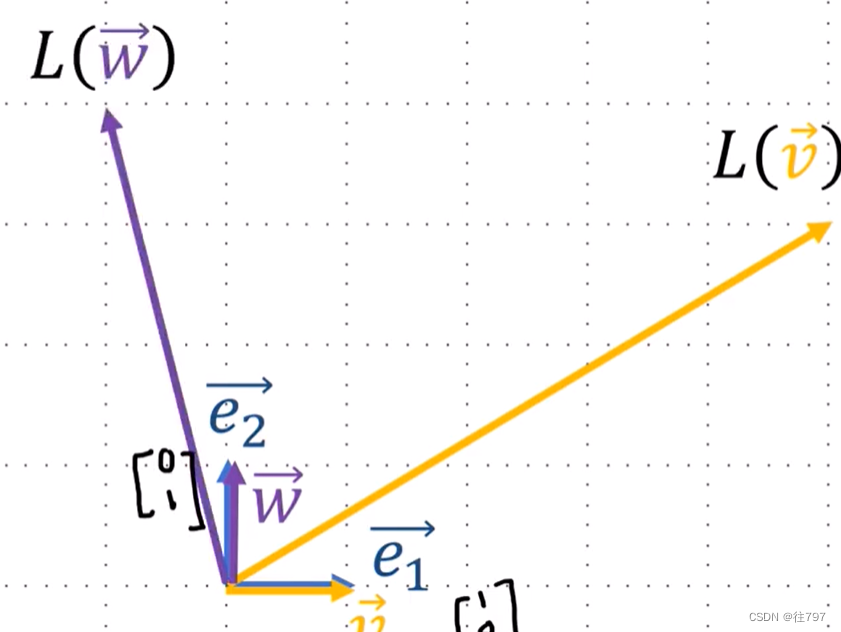
注意到,基向量没有移动,因为线性映射不会改变基底,我们仍用相同的基底测量输出向量,
所以,综上,矩阵是线性映射的坐标解释。
2.几何定义(线性映射视为图片)
线性映射 是 空间转换,并且保持线平行, 保持线间隔均匀,保持原点静止。
为从视觉上了解它的外观,从2D空间开始,上面有一堆网格线:
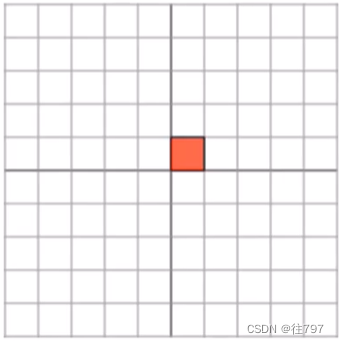 (初始的输入空间?)
(初始的输入空间?)
这里有三个线性映射的例子:
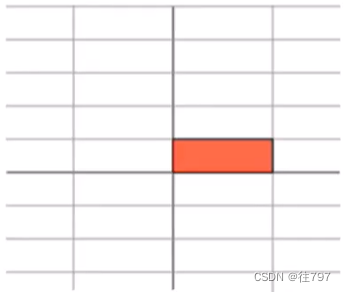
所以,上面这个线性映射基本上只是水平方向的拉伸。
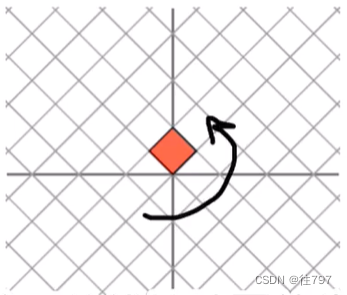 这个线性映射像一个旋转,
这个线性映射像一个旋转,
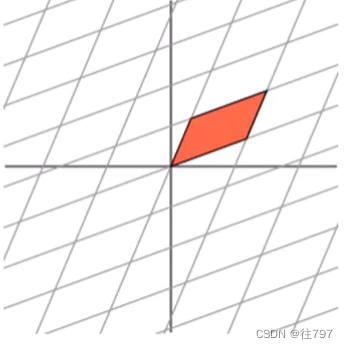
这个线性映射像做一个倾斜变换(可把它想象成在这个方向上做一个旋转,然后沿着这个轴伸展)。
正如上面这些图所示,在所有这些情况下, 输出空间中的网格线仍然彼此平行, 都是均匀分布的(即使间距与输入空间不同),并且原点没有移动。
所有的上面这些都是线性映射可以做到的。
(注意,在该定义下,translation are not linear maps------平移不是线性映射。即使平移能使得网格线平行,间距均匀,但平移会移动原点,所以平移不是线性映射)
所以,这就是可视化的几何定义。
3.抽象定义(纯代数)
线性映射 是将 向量 映射 到 向量 的函数。
在该情况下,现有一映射L将 向量从向量空间V 映射到 向量空间W,我们很多例子涉及到的映射是从空间V映射到 空间V, 但一般来说,输入和输出空间可以不同。
且线性映射在这里遵循两个属性:
1、可添加线性映射的输入或输出并得到相同的答案。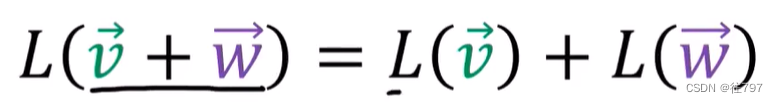
2.可缩放输入或缩放输出并得到相同的答案。
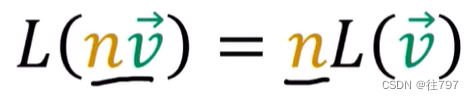
这两个属性被称为“线性”、 。 所以协向量和线性映射都是线性函数。唯一的区别是:协向量输出一个标量,线性映射输出向量。
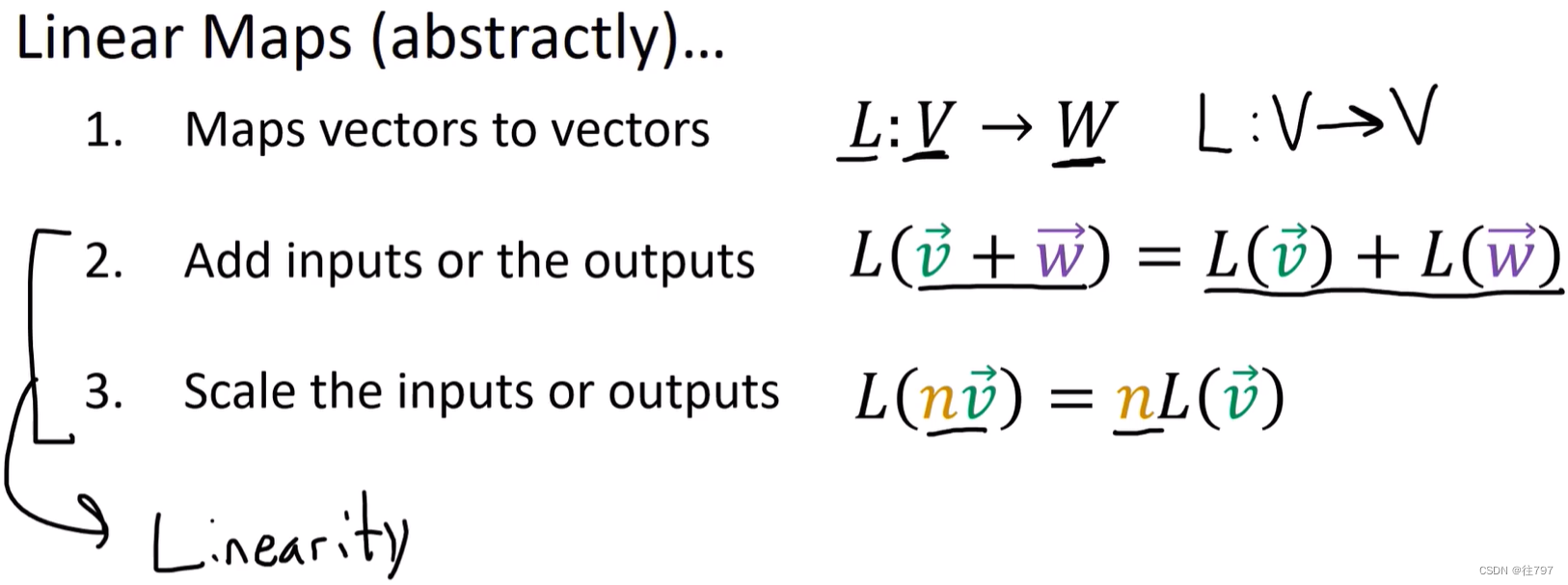
下面展示 这个抽象定义 如何 与我们看到的其他定义相关联。
如前所说,有这个属性:
![]()
现展示它的几何意义,在网格上绘制输入变量,这里我们有绿色的向量v和紫色的向量w,
v+w 用黑色表示。
现展示这图中的三个线性映射是如何服从这个代数性质的。

在这些所有的输出空间中可以看到,加法定律仍然有效,
对缩放规则(第二个属性)也做同样的事情。
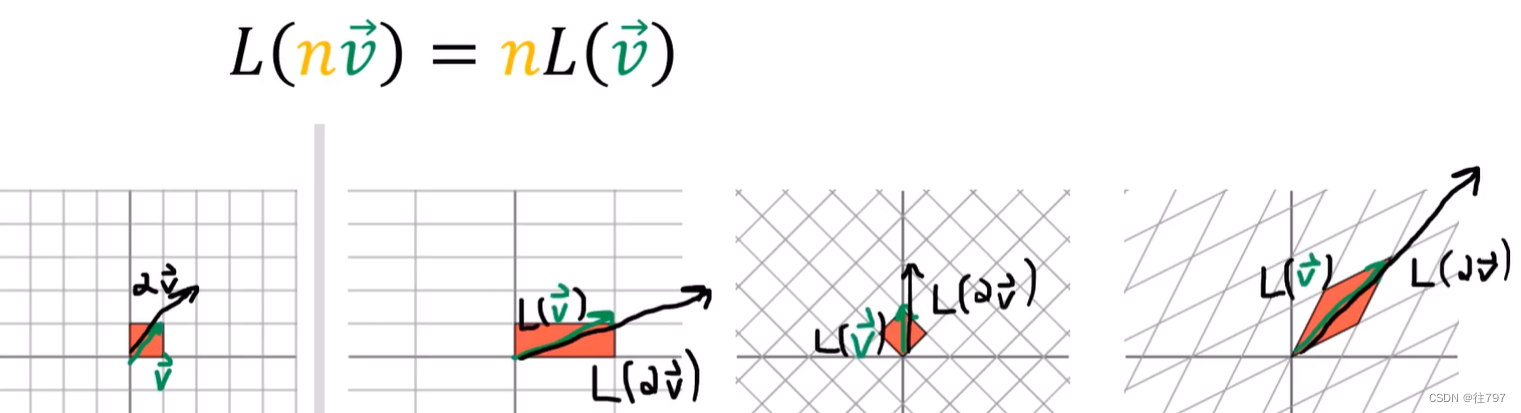
因此,先缩放再转换 与 先转换再缩放 是一回事。
还有一个问题,坐标定义的来源
对于下图这个矩阵乘法公式,若你不知道它背后的原因,它看起来真的很奇怪。
事实证明,矩阵乘法规则实际上来自上面这个抽象定义,
证明:
首先我们有一个线性映射L,它作用于向量V,并产生输出向量W,
若将向量V拓展成它的分量,就能得到
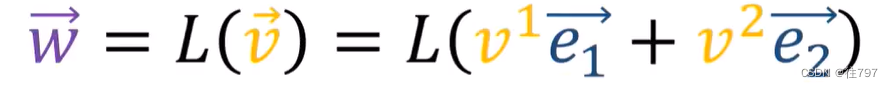
通过L的线性规则,得到: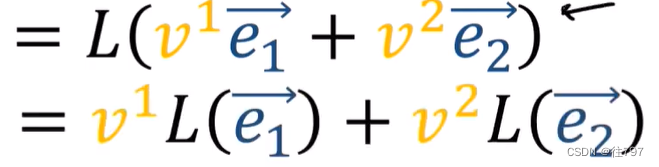
e1、e2是向量,所以你可能会问如何根据 基底e1、e2来表达这些向量,
现做个 简单的假设:
假设线性映射L是从V到V的函数,因此输入空间和输出空间是相同的。
因此,输出空间V仍然具有基底e1、e2,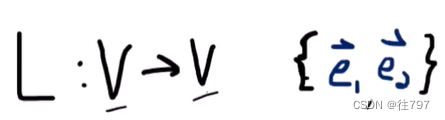
这意味着我们仍然可以将 这些输出向量 写为相同的旧基 e1、e2的线性组合,
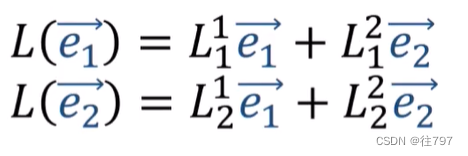
而这些线性组合的系数,
这些L系数帮助我们使用“e”基底向量构建线性映射的输出向量。
所以,可以将输出向量重写为基的线性组合,并且可在此切换内容为以按基向量e1、e2来重新分组,
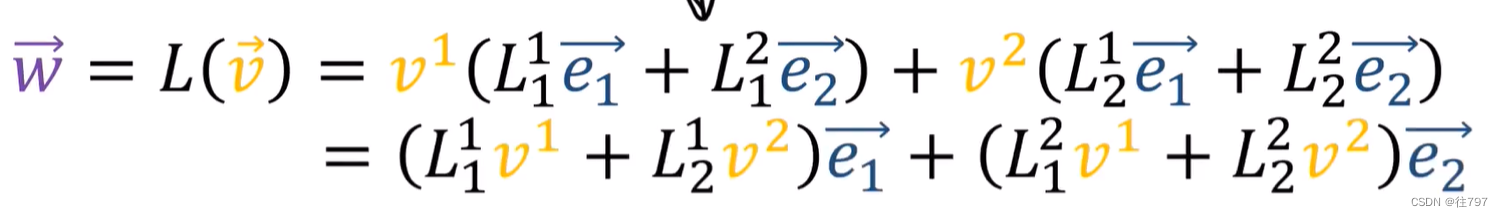
现在,由于将W写成基向量的线性组合,
因此,这些系数 实际上 只是W的分量:w1、w2 ,
所以现在我们已经推到出 如何使用这些公式将V系数转换为W系数,
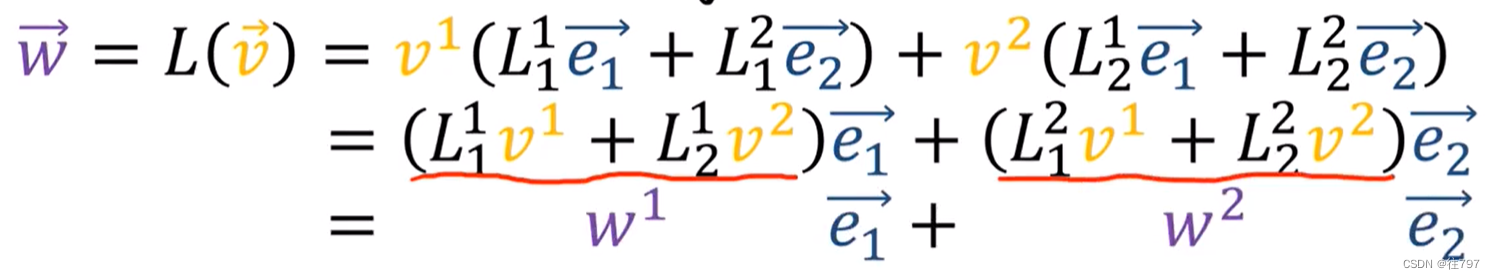
而这些公式 就是那些当你做标准的2x2矩阵乘以一个2x1的列向量。
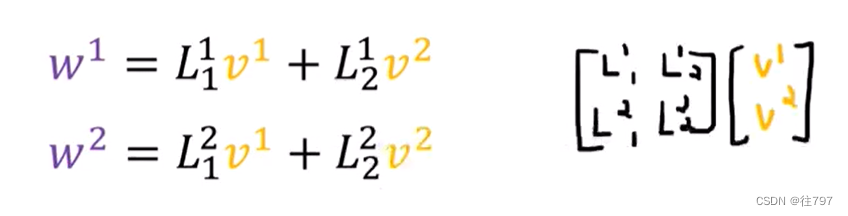
现总结一下,如果我们有一个线性映射L,它可以像这样将向量V转换为另一个向量W,其中W可以写成基底的线性组合,并且我门知道如何使用L系数转换基底(或者说我们知道L如何转换基向量副本可能更好)
这意味着我们可以在这里使用这些公式将V分量变为W分量。
如果对任意数量的维度重复这个论点,如果我们有一个n维的线性映射L,
我们将从这里的公式中得到所有的L系数,然后可以使用这个公式将V分量转换为W分量,

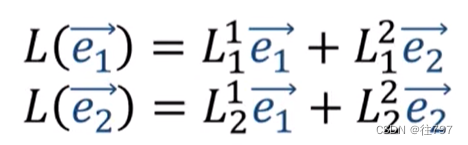
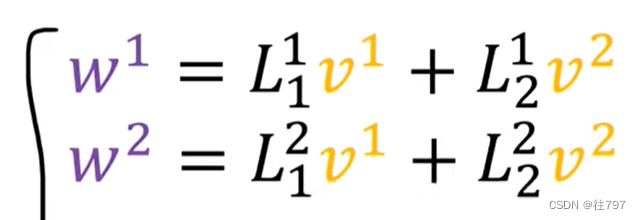
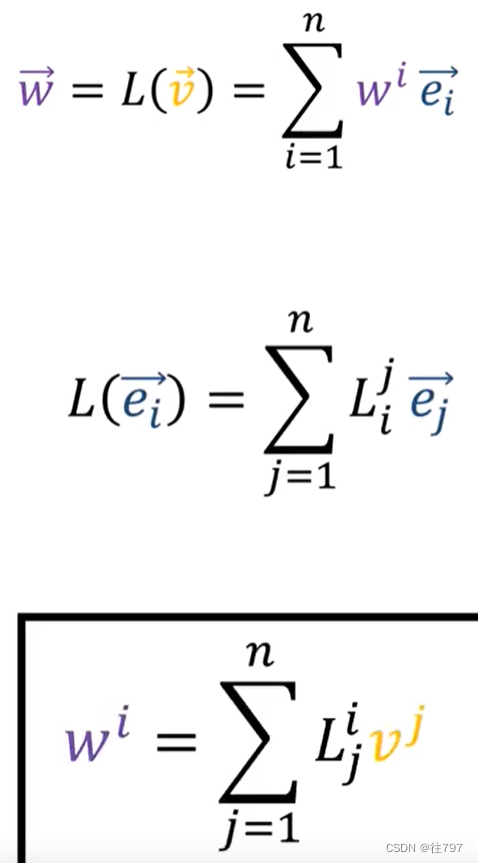
相关文章:
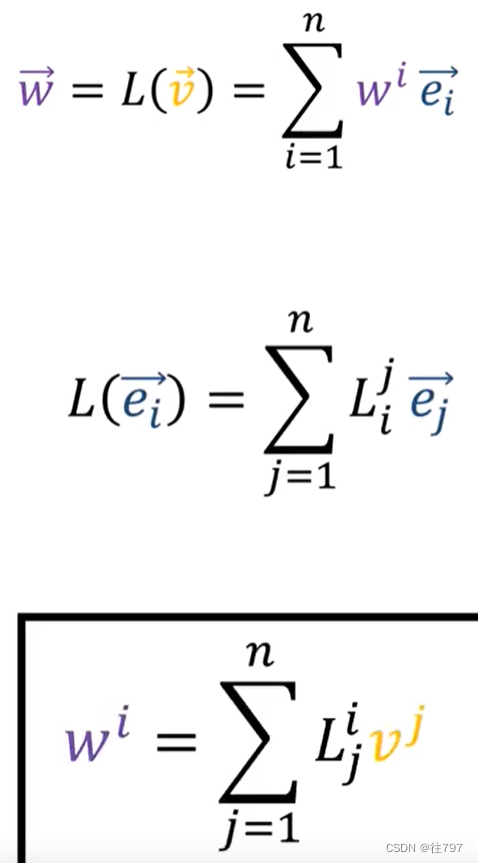
9.Linear Maps
线性映射 线性映射是将向量作为输入并产生一些新向量作为输出的转换。 从坐标定义开始(数组),再到2,3,并展示它们是如何关联的 线性映射的坐标表示最终是矩阵, 1.坐标定义(数组) 列向量是向量的坐标表示…...

大数据Doris(十):添加BE步骤
文章目录 添加BE步骤 一、使用mysql连接 二、添加be...

Vue2 +Element UI 表格行合并
如果相邻数据是一致的,则单元格的行合并,指定需要合并的列,下面我是指定合并了分类和类型这两列。 先看效果 Element UI为我们的<el-table>提供了一个属性span-method:合并行或列的计算方法 下面是一个示例: html部分 - 主要是在表上指…...

SuperEdge易学易用系列-一键搭建SuperEdge集群
条件说明: 系统 公网IP 内网IP 服务器所在地 K8S版本 Centos7.9 114.116.101.254 192.168.0.245 北京 v1.22.6 Centos7.9 119.8.1.96 192.168.0.83 香港 v1.22.6 Ubuntu22 94.74.108.152 192.168.0.154 纽约 v1.22.6 1. 开始部署 1.1 两条指令从零搭建一个边缘集…...
农场养殖农产品商城小程序搭建
鸡鸭羊牛鱼养殖用户不少,其规模也有大有小,尤其对一些生态养殖企业,其产品需求度更高,同时他们也有实际的销售需求。 由于具备较为稳定的货源,因此大规模多规格销售属性很足。 通过【雨科】平台搭建农场养殖商城&…...
大语言模型之十七-QA-LoRA
由于基座模型通常需要海量的数据和算力内存,这一巨大的成本往往只有巨头公司会投入,所以一些优秀的大语言模型要么是大公司开源的,要么是背后有大公司身影公司开源的,如何从优秀的开源基座模型针对特定场景fine-tune模型具有广大的…...
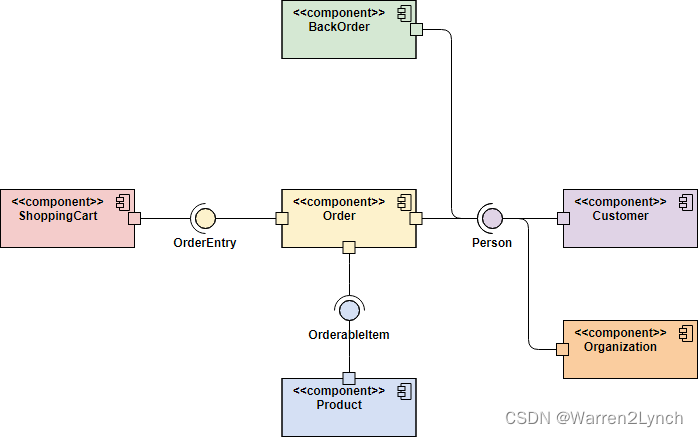
UML组件图综合指南:设计清晰、可维护的软件系统
介绍: UML(Unified Modeling Language)组件图是软件系统设计中的重要工具,用于描绘系统的物理结构和组件之间的关系。在软件工程中,通过创建清晰的组件图,团队能够更好地理解系统的模块化结构和组织关系&a…...
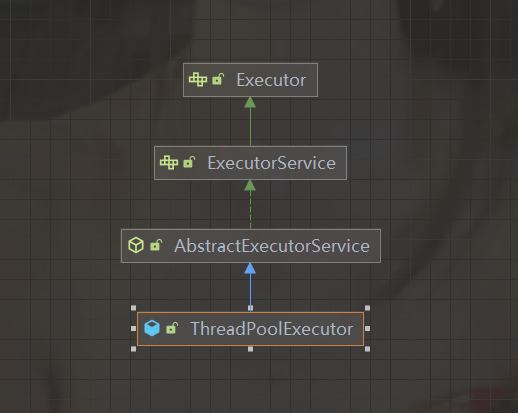
深入浅出ThreadPoolExecutor(一)
文章目录 线程池简诉ThreadPoolExecutor详解ThreadPoolExecutor参数详解创建线程池的工具类Executors 线程池简诉 针对各种池子,比如 连接池:用于管理和重复使用数据库连接,避免频繁创建和销毁数据库连接带来的性能开销。对象池:用于管理和重复使用对象…...

网站的常见攻击与防护方法
在互联网时代,几乎每个网站都存在着潜在的安全威胁。这些威胁可能来自人为失误,也可能源自网络犯罪团伙所发起的复杂攻击。无论攻击的本质如何,网络攻击者的主要动机通常是谋求经济利益。这意味着无论您经营的是电子商务项目还是小型商业网站…...
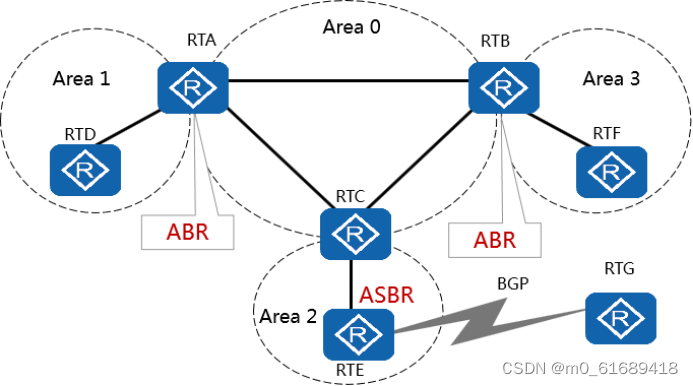
网络工程师知识点3
41、各个路由协议,在华为设备中的优先级? 直连路由 0 OSPF 10 静态 60 42、OSPF:开放式最短路径优先路由协议,使用SPF算法发现和计算路由 OSPF的优点: 1、收敛速度快,无路由自环,适用于大型网络…...
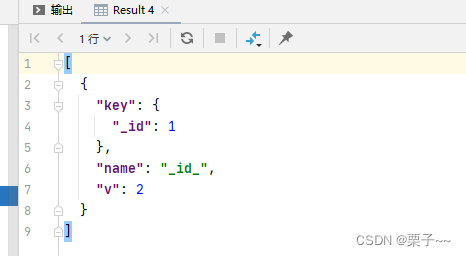
mongoDB 性能优化
文章目录 前言mongoDB 性能优化1. explain方法来查看查询的执行计划2. 查看mongoDB 集合的索引3. mongoDB 怎么添加索引4. 升序索引与降序索引是什么意思 前言 如果您觉得有用的话,记得给博主点个赞,评论,收藏一键三连啊,写作不易…...

10月13日,每日信息差
今天是2023年10月13日,以下是为您准备的13条信息差 第一、欧盟投资4.5亿欧元在法国建设电池超级工厂。欧洲投资银行是欧盟的贷款机构,也是世界上最大的跨国银行之一 第二、北京银行推出数字人民币智能合约平台 数字人民币预付资金管理产品在商超场景…...

Spring Boot 中的 Redis 数据操作配置和使用
Spring Boot 中的 Redis 数据操作配置和使用 Redis(Remote Dictionary Server)是一种高性能的开源内存数据库,用于缓存、消息队列、会话管理和数据存储。在Spring Boot应用程序中,Redis被广泛用于各种用例,包括缓存、…...

rust宏
宏看起来和函数很像,只不过名称末尾有一个感叹号 ! 。 宏并不产生函数调用,而是展开成源码,并和程序的其余部分一起被编译。 Rust宏和C不同,Rust的宏会展开为抽象语法树(AST,abstract syntax treeÿ…...
性能测试之性能测试指标详解
前言 刚开始,以为做性能测试,就是做些脚本、参数化、关联,压起来之后,再扔出一个结果。 但实际上不止这些内容,还要加上性能分析,关注调优之后响应时间有多大的提升,TPS 有多大的提高…...

CustomNavBar 自定义导航栏视图
1. 创建偏好设置键 CustomNavBarTitlePreferenceKey.swift import Foundation import SwiftUI//State private var showBackButton: Bool true //State private var title: String "Title" //"" //State private var subtitle: String? "SubTitl…...

canal rocketmq
上篇文章canal 消费进度说到直接使用ClusterCanalConnector并发消费是有问题的,可以先用单点将canal事件发送到mq中,再由mq并发处理,另外mq还可以做到削峰的作用,让canal数据不至于阻塞。 使用队列,可以自己起一个单实…...
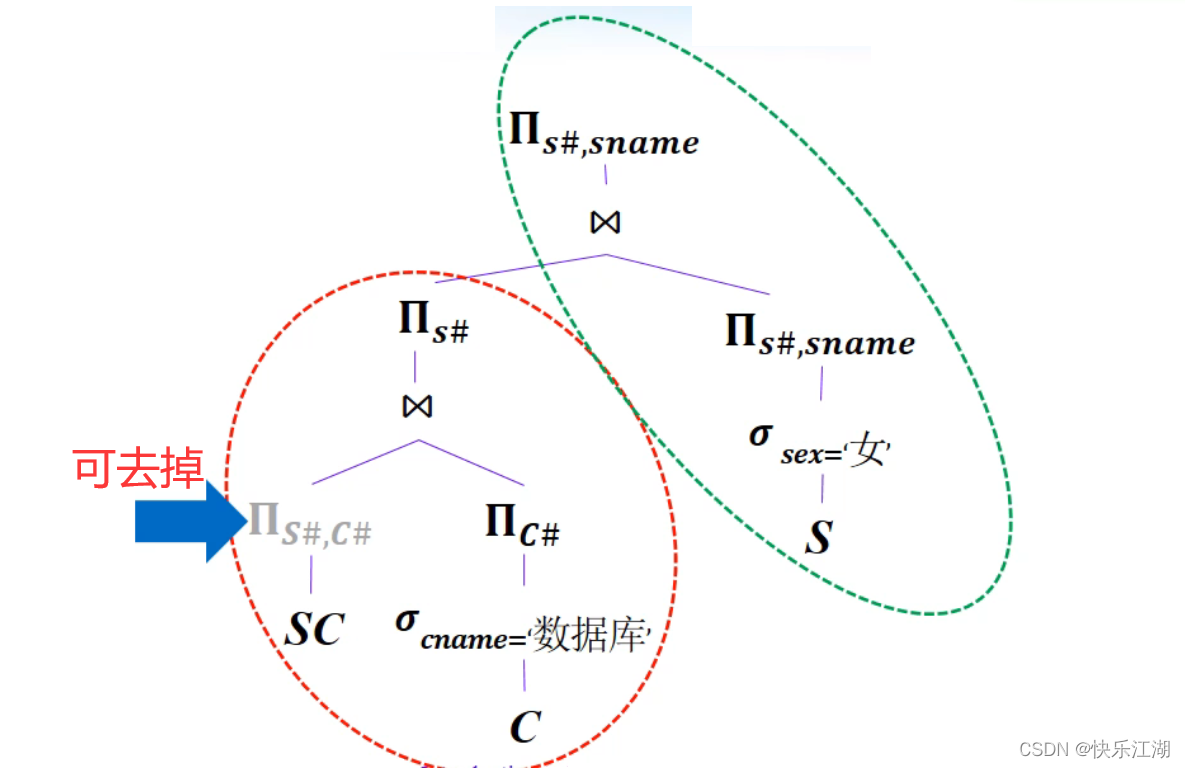
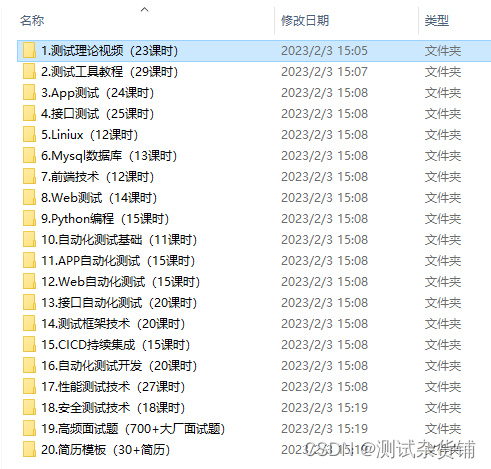
【数据库系统概论】第九章关系查询处理何查询优化
9.1查询处理 一:查询处理步骤 关系数据库管理系统查询处理可以分为4个阶段: 查询分析查询检查查询优化查询执行 (1)查询分析 任务:对查询语句进行扫描,分析词法、语法是否符合SQL语法规则 如果没有语…...

bp盐丘模型波场数值模拟matlab
波场数值模拟是地震勘探和地震学研究中常用的工具,而BP(Backpropagation)盐丘模型是一种用于地下介质成像的方法。如果您想在MATLAB中进行波场数值模拟,并结合BP盐丘模型进行地下成像,可以按照以下步骤进行:…...
结构体对齐规则
1.第一个成员在结构体变量偏移量为0的地址处。 2.其他成员变量对齐到某个数字(对齐数)的整数倍的地址处。(对齐数编译器默认的一个对齐数与该成员大小的较小值)注意:目前有且只有VS编译器有默认为8. 3.结构体总大小为最大对齐数的整数倍。 4.如果嵌套…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
