【算法】三道算法题两道难度中等一道困难
算法目录
- 只出现一次的数字(中等难度)
- java解答参考
- 二叉树的层序遍历(难度中等)
- java 解答参考
- 给表达式添加运算符(比较困难)
- java解答参考
大家好,我是小冷。
上一篇是算法题目
接下来继续看下算法题目吧,用Java解答,可能更能激发一下大脑思考。
只出现一次的数字(中等难度)
题目要求:
给你一个整数数组 nums ,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。
示例 1:
输入:nums = [2,2,3,2]
输出:3
示例 2:
输入:nums = [0,1,0,1,0,1,99]
输出:99
提示:
1 <= nums.length <= 3 * 104
-231 <= nums[i] <= 231 - 1
nums 中,除某个元素仅出现 一次 外,其余每个元素都恰出现 三次
根据题目要求和实例可分析有哪些步骤,需要几个for循环。
进阶:你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗?
java解答参考
class Solution {public int singleNumber(int[] nums) {int ret = 0;for (int i = 0; i < 32; ++i) {int bitnums = 0;int bit = 1 << i;for (int num : nums) {if ((num & bit) != 0)bitnums++;}if (bitnums % 3 != 0)ret |= bit;}return ret;}
}
二叉树的层序遍历(难度中等)
题目要求:
给你一个二叉树,请你返回其按 层序遍历 得到的节点值。 (即逐层地,从左到右访问所有节点)。
示例:
二叉树:[3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
返回其层序遍历结果:
[
[3],
[9,20],
[15,7]
]
java 解答参考
public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}
class Solution {public List<List<Integer>> levelOrder(TreeNode root) {List<List<Integer>> l = new ArrayList<>();Queue<TreeNode> q = new LinkedList<TreeNode>();if (root != null) {q.add(root);}while (!q.isEmpty()) {List<Integer> l2 = new ArrayList<>();int number = q.size();while (number > 0) {TreeNode t = q.poll();l2.add(t.val);if (t.left != null) {q.add(t.left);}if (t.right != null) {q.add(t.right);}number--;}l.add(l2);}return l;}
}
给表达式添加运算符(比较困难)
题目要求:
给定一个仅包含数字 0-9 的字符串 num 和一个目标值整数 target ,在 num 的数字之间添加 二元 运算符(不是一元)+、- 或 * ,返回所有能够得到目标值的表达式。
示例 1:
输入: num = “123”, target = 6
输出: [“1+2+3”, “123”]
示例 2:
输入:
num =
“232”, target = 8
输出: [“23+2", "2+32”]
示例 3:
输入:
num =
“105”, target = 5
输出: [“1*0+5”,“10-5”]
示例 4:
输入:
num =
“00”, target = 0
输出: [“0+0”, “0-0”, “0*0”]
示例 5:
输入:
num =
“3456237490”, target = 9191
输出: []
提示:
1 <= num.length <= 10
num 仅含数字
-231 <= target <= 231 - 1
java解答参考
class Solution {int n;String num;List<String> ans;int target;public List<String> addOperators(String num, int target) {this.n = num.length();this.num = num;this.target = target;this.ans = new ArrayList<String>();StringBuffer expr = new StringBuffer();dfs(expr, 0, 0, 0);return ans;}public void dfs(StringBuffer sba, long sum, long prepareMultiply, int index) {StringBuffer sb = new StringBuffer(sba);if (index == n) {if (sum == target) {ans.add(sb.toString());}return;}int sign = sb.length();if (index > 0) {sb.append("0");}long val = 0;for (int i = index; i < n && (i == index || num.charAt(index) != '0'); i++) {val = val * 10 + (num.charAt(i) - '0');sb.append(num.charAt(i));if (index == 0) {dfs(sb, val, val, i + 1);continue;}sb.setCharAt(sign, '+');dfs(sb, sum + val, val, i + 1);sb.setCharAt(sign, '-');dfs(sb, sum - val, -val, i + 1);sb.setCharAt(sign, '*');dfs(sb, sum - prepareMultiply + prepareMultiply * val, prepareMultiply * val, i + 1);}}
}
好了,今天学习在这里,小冷一直在技术路上前行…
昨天,删去;今天,争取;明天,努力
需要资料的VX 搜索 小冷coding 关注或者点击下方名片扫码 获取
相关文章:

【算法】三道算法题两道难度中等一道困难
算法目录只出现一次的数字(中等难度)java解答参考二叉树的层序遍历(难度中等)java 解答参考给表达式添加运算符(比较困难)java解答参考大家好,我是小冷。 上一篇是算法题目 接下来继续看下算法题…...
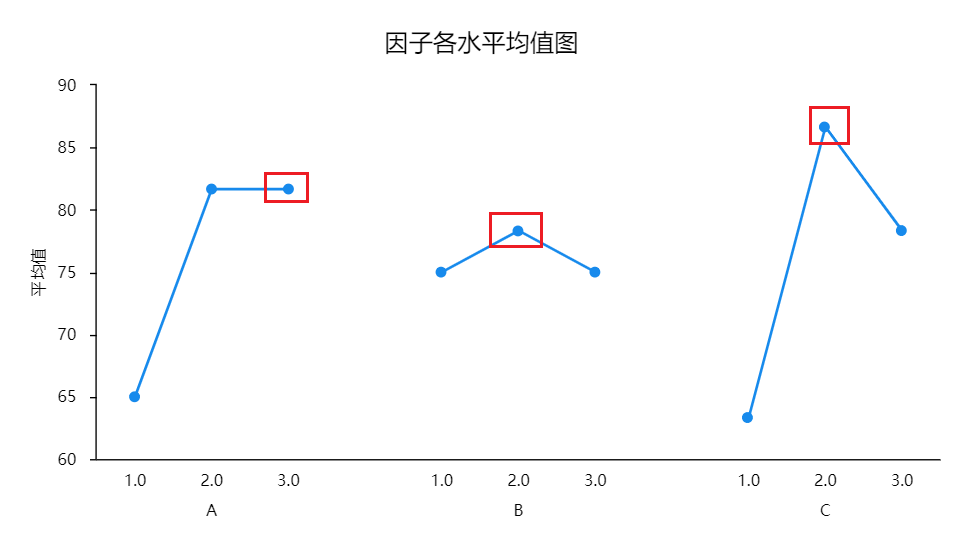
正交实验与极差分析
正交试验极差分析流程如下图: 正交试验说明 正交试验是研究多因素试验的设计方法。对于多因素、多水平的实验要求,如果每个因素的每个水平都要进行试验,这样就会耗费大量的人力和时间,正交试验可以选择出具有代表性的少数试验进行…...
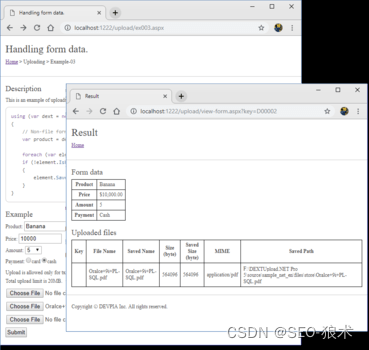
DEXTUpload .NET增强的上传速度和可靠性
DEXTUpload .NET增强的上传速度和可靠性 DEXTUpload.NET Pro托管在Windows操作系统上的Internet Information Server(IIS)上,服务器端组件基于HTTP协议,支持从web浏览器到web服务器的文件上载。它也可以在ASP.NET服务器应用程序平台开发的任何网站上使用…...
)
SkyWalking 将方法加入追踪链路(@Trace)
SkyWalking8 自定义链路追踪@Trace 自定义链路,需要依赖skywalking官方提供的apm-toolkit-trace包.在pom.xml的dependencies中添加如下依赖: <dependency><groupId>org.apache.skywalking</groupId><artifactId>apm-toolkit-trace</artifactId>&…...
MySQL Administrator定时备份MySQL数据库
1、下载并安装软件mysql-gui-tools-5.0-r17-win32.exe 2、将汉化包zh_CN文件夹拷贝到软件安装目录 3、菜单中打开MySql Adminstrator,见下图,初次打开无服务实例。 点击已存储连接右侧按钮①,打开下图对话框。点击“新连接”按钮ÿ…...

Kubernetes入门教程 --- 使用二进制安装
Kubernetes入门教程 --- 使用二进制安装1. Introduction1.1 架构图1.2 关键字介绍1.3 简述2. 使用Kubeadm Install2.1 申请三个虚拟环境2.2 准备安装环境2.3 配置yum源2.4 安装Docker2.4.1 配置docker加速器并修改成k8s驱动2.5 时间同步2.6 安装组件3. 基础知识3.1 Pod3.2 控制…...

深度学习模型压缩方法概述
一,模型压缩技术概述 1.1,模型压缩问题定义 因为嵌入式设备的算力和内存有限,因此深度学习模型需要经过模型压缩后,方才能部署到嵌入式设备上。 模型压缩问题的定义可以从 3 角度出发: 模型压缩的收益: 计算: 减少浮点运算量(FLOPs),降低延迟(Latency)存储: 减少内…...

《NFL橄榄球》:坦帕湾海盗·橄榄1号位
坦帕湾海盗(英语:Tampa Bay Buccaneers)是一支位于佛罗里达州的坦帕湾职业美式橄榄球球队。他们是全国橄榄球联盟的南区其中一支球队。在1976年,与西雅图海鹰成为NFL的球队。球队在最初的两个球季连败26场,在二十世纪七…...
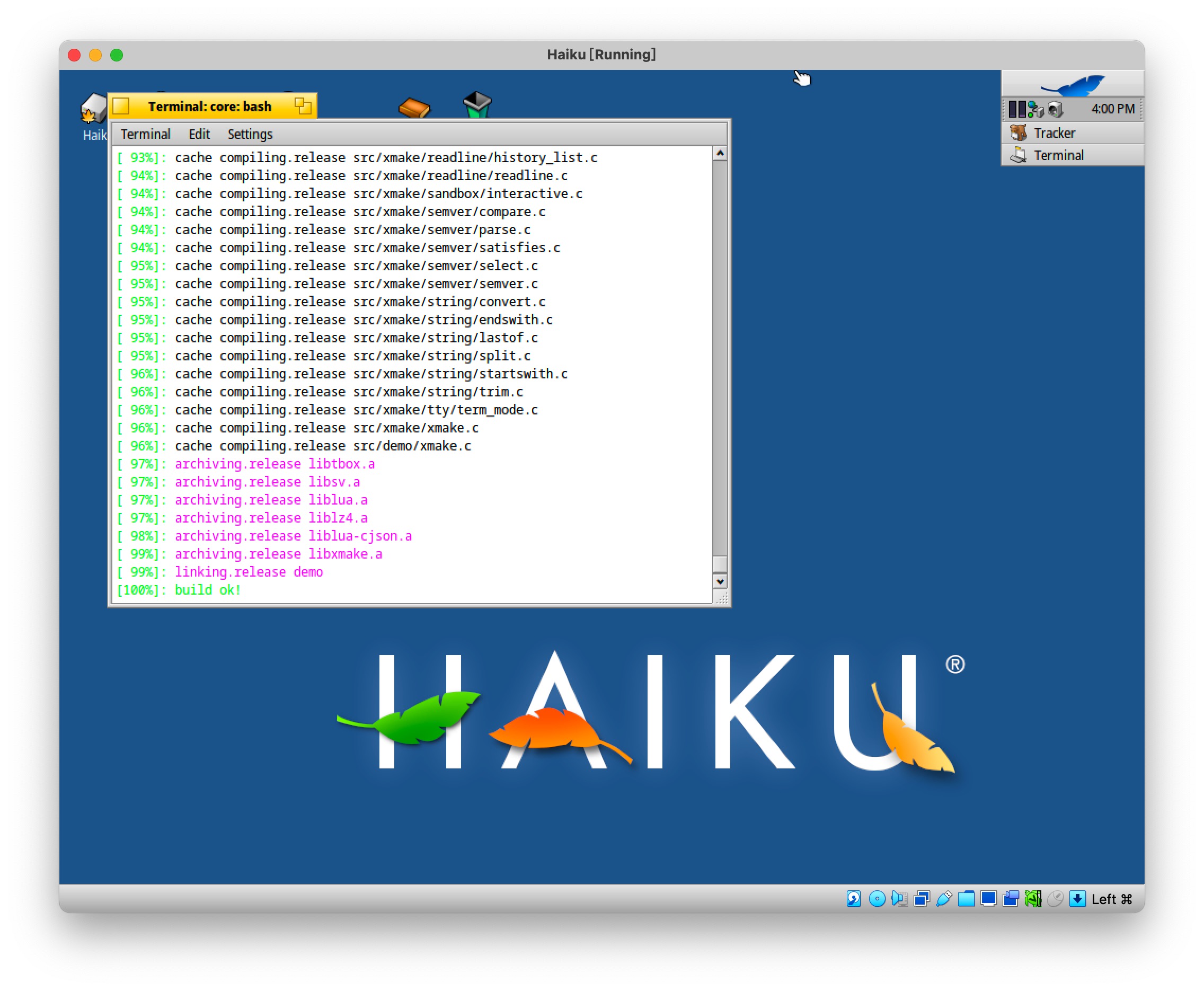
Xmake v2.7.7 发布,支持 Haiku 平台,改进 API 检测和 C++ Modules 支持
layout: post.cn title: “Xmake v2.7.7 发布,支持 Haiku 平台,改进 API 检测和 C Modules 支持” tags: xmake lua C/C package modules haiku cmodules categories: xmake Xmake 是一个基于 Lua 的轻量级跨平台构建工具。 它非常的轻量,没…...

苹果ios签名证书的生成方法
在使用hbuilderx打包uniapp或html5应用的时候,假如是打包ios应用,是需要ios签名证书,和证书profile文件的,这个证书要求是p12格式的证书,profile文件又叫描述文件。 这两个文件,需要在苹果开发者中心生成&…...

c++开发配置常用网站记录
1.ubuntu 镜像源: (1) 清华源:https://mirror.tuna.tsinghua.edu.cn/help/ubuntu/ (2) 阿里源:https://developer.aliyun.com/mirror/ubuntu?spma2c6h.13651102.0.0.3e221b11VuM27s 包含了ubuntu各个版本的source源 2.ubuntu iso镜像下载…...
DC-1 靶场学习
以前写过了,有一些忘了,快速的重温一遍。 DC一共九个靶场,目标一天一个。 文章目录环境配置:信息搜集:漏洞复现:FLAG获取环境配置: 最简单的办法莫过于将kali和DC-1同属为一个nat的网络下。 信…...

oracle 不使用索引深入解析
首先,我们要确定数据库运行在何种优化模式下,相应的参数是:optimizer_mode。缺省的设置应是"choose",即如果对已分析的表查询的话选择CBO,否则选择RBO。如果该参数设为“rule”,则不论表是否分析…...

什么是自助式BI工具,有没有推荐
为什么需要自助式BI? 传统的BI采用的是“业务提报表需求,IT进行开发”的模式。决策管理者和业务人员提出用报表等来展示经营管理数据的需求;接着IT响应需求,进行需求沟通、数据处理加工、报表开发等主体工作;最后决策管…...

如何高效管理自己的时间,可以从这几个方向着手
如果你是上班族,天选打工人,你的绝大多数时间都属于老板,能够自己支配的时间其实并不多,所以你可能察觉不到时间管理的重要性。但如果你是自由职业者或者创业者,想要做出点成绩,那你就需要做好时间管理&…...
)
【PAT甲级题解记录】1014 Waiting in Line (30 分)
【PAT甲级题解记录】1014 Waiting in Line (30 分) 前言 Problem:1014 Waiting in Line (30 分) Tags:模拟 双端队列 Difficulty:剧情模式 想流点汗 想流点血 死而无憾 Address:1014 Waiting in Line (30 分) 问题描述 银行有N个…...

web接入大华摄像头实时视频
目录 一、FFmpeg下载及配置 二、nginx下载及配置 三、摄像rtsp取流 四、ffmpeg推流 五、html前端工作 一、FFmpeg下载及配置 地址:Download FFmpeg 下载并解压FFmpeg文件夹,配置环境变量:在“Path”变量原有变量值内容…...
Git代码冲突-不同分支之间的代码冲突
1、解决思路在团队开发中,提交代码到Git仓库时经常会遇到代码冲突的问题。- 原因:多人对相同的文件进行了编辑,造成代码存在差异化- 解决方案:1. 使用工具或git命令对比不同分支代码的差异化2. 把不同分支中有效代码进行保留&…...
KUKA KR C4机器人与S7-1200PLC进行PROFINET通信的具体方法和步骤
KUKA KR C4机器人与S7-1200PLC进行PROFINET通信的具体方法和步骤 首先,从KUKA机器人控制柜中将KOP备选软件包拷贝出来,然后在“WorkVisual Development Environment”安装KUKA备选软件包(版本非常重要,尽量从控制柜中拷贝), 也可以从以下链接中获取: KUKA机器人PROFINET…...

从0到1一步一步玩转openEuler--24 openEuler管理进程-调度启动进程
文章目录24 openEuler管理进程-调度启动进程24.1 定时运行一批程序(at)24.1.1 at命令24.1.2 设置时间24.1.3 执行权限24.2 周期性运行一批程序(cron)24.2.1 运行机制24.2.2 crontab命令24.2.3 crontab文件24.2.4 编辑配置文件操作…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

英国云服务器上安装宝塔面板(BT Panel)
在英国云服务器上安装宝塔面板(BT Panel) 是完全可行的,尤其适合需要远程管理Linux服务器、快速部署网站、数据库、FTP、SSL证书等服务的用户。宝塔面板以其可视化操作界面和强大的功能广受国内用户欢迎,虽然官方主要面向中国大陆…...
