强连通分量+缩点
[图论与代数结构 701] 强连通分量
题目描述
给定一张 n n n 个点 m m m 条边的有向图,求出其所有的强连通分量。
注意,本题可能存在重边和自环。
输入格式
第一行两个正整数 n n n , m m m ,表示图的点数和边数。
接下来 m m m 行,每行两个正整数 u u u 和 v v v 表示一条边。
输出格式
第一行一个整数表示这张图的强连通分量数目。
接下来每行输出一个强连通分量。第一行输出 1 号点所在强连通分量,第二行输出 2 号点所在强连通分量,若已被输出,则改为输出 3 号点所在强连通分量,以此类推。每个强连通分量按节点编号大小输出。
样例 #1
样例输入 #1
6 8
1 2
1 5
2 6
5 6
6 1
5 3
6 4
3 4
样例输出 #1
3
1 2 5 6
3
4
提示
对于所有数据, 1 ≤ n ≤ 10000 1 \le n \le 10000 1≤n≤10000, 1 ≤ m ≤ 100000 1 \le m \le 100000 1≤m≤100000。
#include <bits/stdc++.h>using namespace std;
const int N = 2e5 + 5;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef array<ll, 3> p3;
int mod = 998244353;
const int maxv = 4e6 + 5;
// #define endl "\n"int n,m,tot,dfsn[N],ins[N],low[N];
stack<int> s;vector<int> e[N];
vector< vector<int> > scc;
vector<int> b(N);
void dfs(int x)
{low[x]=dfsn[x]=++tot,ins[x]=1,s.push(x);for(auto u: e[x]){if(!dfsn[u]){dfs(u);low[x]=min(low[x],low[u]);}else if(ins[u]) low[x]=min(low[x],dfsn[u]);}if(dfsn[x]==low[x]){vector<int> c;while(1){auto t=s.top();c.push_back(t);ins[t]=0;s.pop();b[t]=scc.size();if(t==x) break;}sort(c.begin(),c.end());scc.push_back(c);}
}void add(int u,int v)
{e[u].push_back(v);
}void solve()
{ int n,m;cin>>n>>m;for(int i=1;i<=m;i++){int u,v;cin>>u>>v;add(u,v);}for(int i=1;i<=n;i++){if(!dfsn[i]){dfs(i);}}cout<<scc.size()<<endl;vector<int> vis(N);for(int i=1;i<=n;i++){int x=b[i];if(vis[x]) continue;vis[x]=1;for(auto r: scc[x]) cout<<r<<" ";cout<<endl;}
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t=1;//cin>>t;while(t--){solve();}system("pause");return 0;
}
【模板】缩点
题目描述
给定一个 n n n 个点 m m m 条边有向图,每个点有一个权值,求一条路径,使路径经过的点权值之和最大。你只需要求出这个权值和。
允许多次经过一条边或者一个点,但是,重复经过的点,权值只计算一次。
输入格式
第一行两个正整数 n , m n,m n,m
第二行 n n n 个整数,其中第 i i i 个数 a i a_i ai 表示点 i i i 的点权。
第三至 m + 2 m+2 m+2 行,每行两个整数 u , v u,v u,v,表示一条 u → v u\rightarrow v u→v 的有向边。
输出格式
共一行,最大的点权之和。
样例 #1
样例输入 #1
2 2
1 1
1 2
2 1
样例输出 #1
2
提示
对于 100 % 100\% 100% 的数据, 1 ≤ n ≤ 1 0 4 1\le n \le 10^4 1≤n≤104, 1 ≤ m ≤ 1 0 5 1\le m \le 10^5 1≤m≤105, 0 ≤ a i ≤ 1 0 3 0\le a_i\le 10^3 0≤ai≤103。
我们对有向图进行缩点后,整个图就变为了DAG,即有向无环图,我们就可以在有向无环图上进行一些DP的操作,显然对于一个有向无环图,我们很容易得到这个题的状态转移:
d p [ i ] = m a x ( d p [ i ] , d p [ j ] + s [ i ] ) , s 为缩点后的点权, j 为 i 的前驱节点 dp[i]=max(dp[i],dp[j]+s[i]),s为缩点后的点权,j为i的前驱节点 dp[i]=max(dp[i],dp[j]+s[i]),s为缩点后的点权,j为i的前驱节点
#include <bits/stdc++.h>using namespace std;
const int N = 2e5 + 5;
typedef long long ll;
typedef pair<ll, ll> pll;
typedef array<ll, 3> p3;
// int mod = 998244353;
const int maxv = 4e6 + 5;
// #define endl "\n"int n, m, tot, dfsn[N], ins[N], low[N];
stack<int> s;
vector<int> e[N], e2[N];
vector<vector<int>> scc;
vector<int> b(N);
int a[N],z[N];void dfs(int x)
{low[x] = dfsn[x] = ++tot, ins[x] = 1, s.push(x);for (auto u : e[x]){if (!dfsn[u]){dfs(u);low[x] = min(low[x], low[u]);}else if (ins[u])low[x] = min(low[x], dfsn[u]);}if (dfsn[x] == low[x]){vector<int> c;while (1){auto t = s.top();c.push_back(t);ins[t] = 0;s.pop();b[t] = scc.size();z[scc.size()]+=a[t];if (t == x)break;}scc.push_back(c);}
}void add(int u, int v)
{e[u].push_back(v);
}void solve()
{cin >> n >> m ;for(int i=1;i<=n;i++) cin>>a[i];for (int i = 1; i <= m; i++){int u, v;cin >> u >> v;add(u, v);}for (int i = 1; i <= n; i++){if (!dfsn[i]){dfs(i);}}for(int i=1;i<=n;i++){for(auto u: e[i]){if(b[i]!=b[u]){e2[b[i]].push_back(b[u]);}}}vector<int> dp(N);vector<int> vis(N);int t=0;for(int i=0;i<scc.size();i++){dp[i]=z[i];}for(int i=scc.size()-1;i>=0;i--){t++;for(auto u: e2[i]){if(vis[u]!=t){vis[u]=t;if(dp[u]<dp[i]+z[u]){dp[u]=dp[i]+z[u];}}}}int ans=0;for(int i=0;i<scc.size();i++){ans=max(ans,dp[i]);}cout<<ans<<endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;t = 1;// cin>>t;while (t--){solve();}system("pause");return 0;
}
相关文章:

强连通分量+缩点
[图论与代数结构 701] 强连通分量 题目描述 给定一张 n n n 个点 m m m 条边的有向图,求出其所有的强连通分量。 注意,本题可能存在重边和自环。 输入格式 第一行两个正整数 n n n , m m m ,表示图的点数和边数。 接下来…...

如何做系统架构设计
文章目录 1、如何进行架构设计体系架构需求体系架构设计体系架构文档化体系架构复审体系架构实现体系架构演化 2、架构设计注意事项分治原则服务自治拥抱变化可维护性考虑依赖和限制阅读代码注意事项 3、最后 系统架构应该如何设计,从自己做架构的经历来分享一些体…...

L14D6内核模块编译方法
一、内核模块基础代码解析 一个内核模块代码错误仍然会导致的内核崩溃。 GPL协议:开源规定,使用内核一些函数需要 1、单内核的缺点 单内核扩展性差的缺点减小内核镜像文件体积,一定程度上节省内存资源提高开发效率不能彻底解决稳定性低的缺…...
PyTorch入门教学——dir()函数和help()函数的应用
1、简介 已知PyTorch是一个工具包,其中包含许多功能函数。dir()函数和help()函数是学习PyTorch包的重要法宝。 dir():能让我们知道工具包以及工具包中的分隔区有什么东西。help():能让我们知道每个工具是如何使用的,即工具的使用…...

使用Elasticsearch来进行简单的DDL搜索数据
说明:Elasticsearch提供了多种多样的搜索方式来满足不同使用场景的需求,我们可以使用Elasticsearch来进行各种复制的查询,进行数据的检索。 1.1 精准查询 用来查询索引中某个类型为keyword的文本字段,类似于SQL的“”查询。 创…...

【软考】9.3 二叉树存储/遍历/线索/最优/查找/平衡
《树与二叉树》 二叉树的顺序存储结构 顺序存储只适用于完全二叉树和满二叉树,一般二叉树不适用i 2 的左孩子为 2i 4,右孩子为 2i 1 5 二叉树的链式存储结构 链式存储适用于二叉树;空结点用“∧”表示二叉链表:左孩子࿰…...
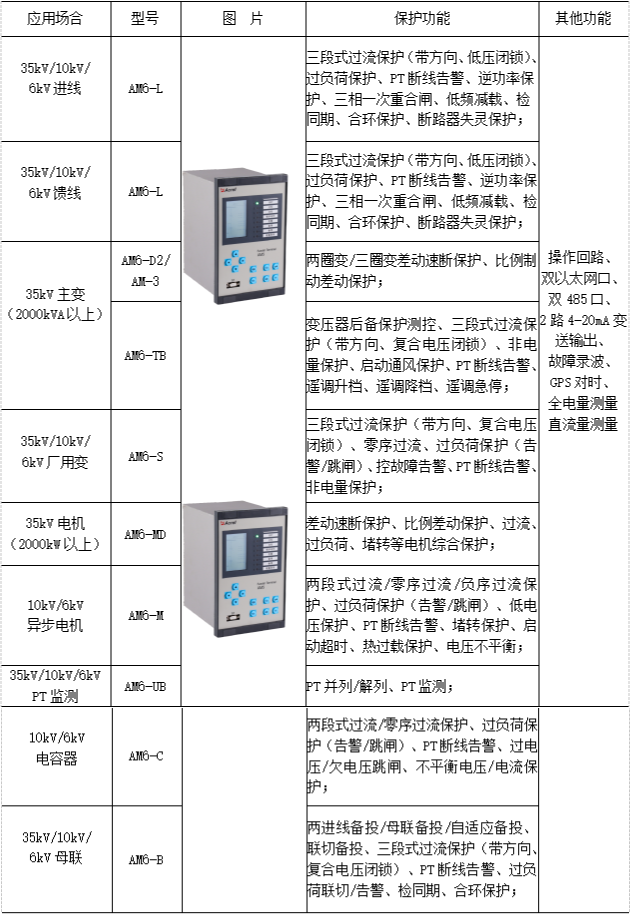
关于矿井地面电力综合自动化系统的研究与产品选型
安科瑞 崔丽洁 摘要:煤矿供电系统是煤矿生产的重要动力保障 , 一旦电力中断 , 生产将被迫停止 , 同时停电后容易发生瓦斯积聚爆炸、淹井等恶性事故,现有配电室采用不同厂商的保护装 置产品,没有形成有效的监控配电系统,不便于管…...
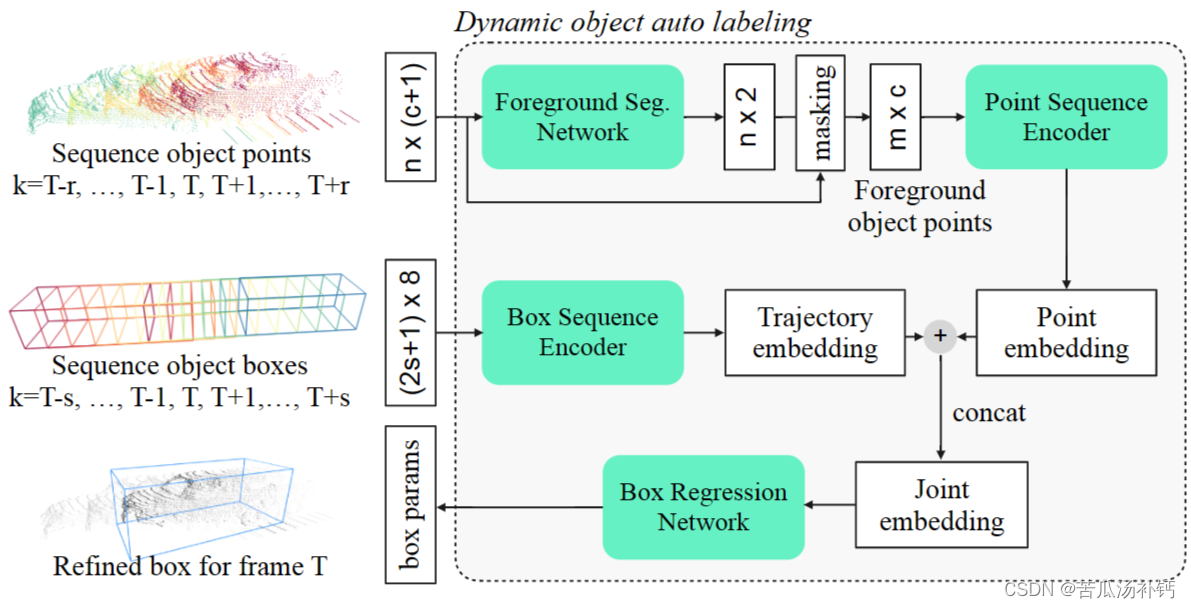
论文阅读:Offboard 3D Object Detection from Point Cloud Sequences
目录 概要 Motivation 整体架构流程 技术细节 3D Auto Labeling Pipeline The static object auto labeling model The dynamic object auto labeling model 小结 论文地址:[2103.05073] Offboard 3D Object Detection from Point Cloud Sequences (arxiv.o…...

Python学习基础笔记六十八——循环
循环是编程语言常见的流程控制。 Python语句要让计算机反复地做一些事情,就要用到循环语句。 有While和for循环。 while循环: command input("请输入命令:") while command ! exit:print(f输入的命令是{command})command input("请输…...
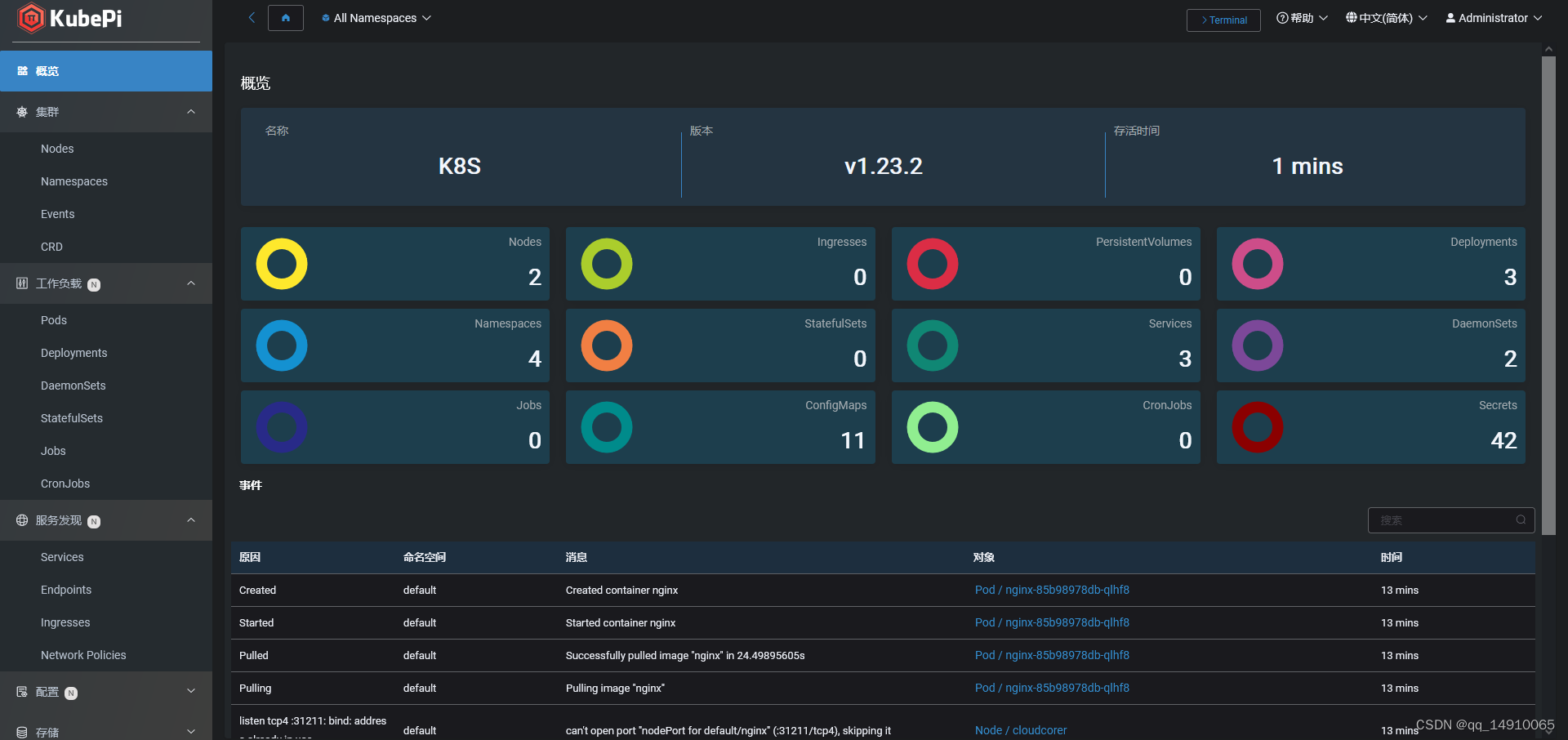
部署k8s dashboard(这里使用Kubepi)
9. 部署k8s dashboard(这里使用Kubepi) Kubepi是一个简单高效的k8s集群图形化管理工具,方便日常管理K8S集群,高效快速的查询日志定位问题的工具 部署KubePI(随便在哪个节点部署,我这里在主节点部署&#…...

Java Lambda表达式的使用
我们了解了 java Lambda 的概念并可以在匿名类的场合使用 Lambda 语法进行简单替换。本节主要介绍在 Java 中如何使用 Lambda 表达式。 作为参数使用Lambda表达式 Lambda 表达式一种常见的用途就是作为参数传递给方法,这需要声明参数的类型声明为函数式接口类型。…...

【初始C语言8】详细讲解初阶结构体的知识
前言 💓作者简介: 加油,旭杏,目前大二,正在学习C,数据结构等👀 💓作者主页:加油,旭杏的主页👀 ⏩本文收录在:再识C进阶的专栏…...
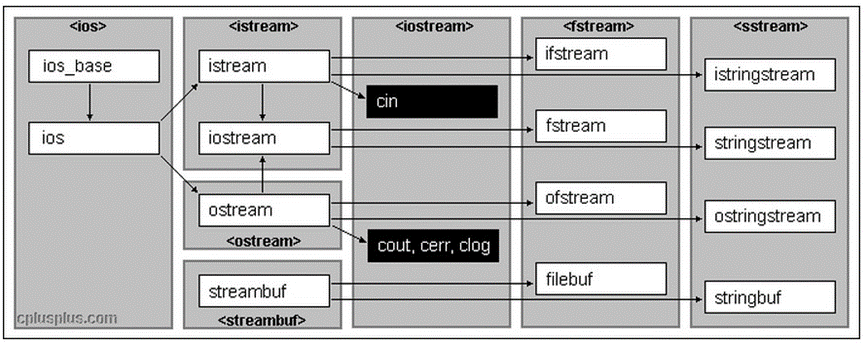
<C++> IO流
C语言的输入与输出 在C语言当中,我们使用最频繁的输入输出方式就是scanf与printf: scanf: 从标准输入设备(键盘)读取数据,并将读取到的值存放到某一指定变量当中。printf: 将指定的数据输出到…...

基于单目相机的2D测量(工件尺寸和物体尺寸)
目录 1.简介 2.基于单目相机的2D测量 2.1 想法: 2.2 代码思路 2.2 主函数部分 1.简介 基于单目相机的2D测量技术在许多领域中具有重要的背景和意义。 工业制造:在工业制造过程中,精确测量是确保产品质量和一致性的关键。基于单目相机的2…...
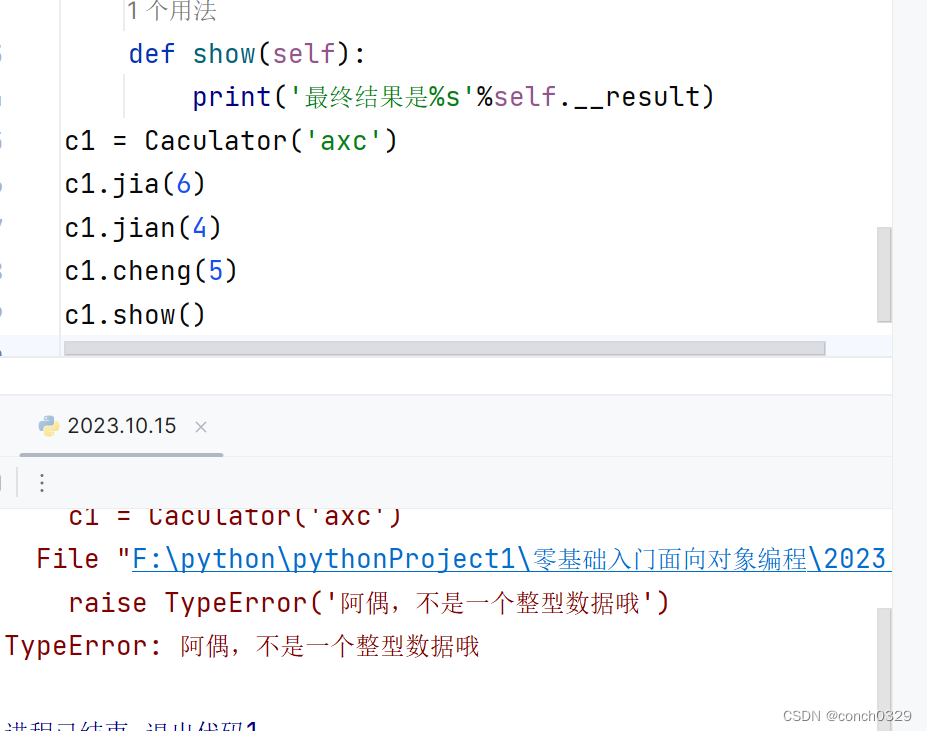
23面向对象案例1
目录 1、计算连续表达式的一个过程 2、优化后的代码 为什么不能return resultn? 3、用面向对象的方法可以解决冗余的问题,但是还是不能解决result的值可以被随意修改的问题 4、解决不能被随意修改的问题,可以将类属性改成私有变量吗&…...

go语言基础之常量与itoa
视频学习地址:Go零基础入门_在线视频教程-CSDN程序员研修院 一. 常量 定义:常量是一个简单值的标识符,在程序运行时,不会被修改的量。注意:常量中的数据类型只可以是布尔型、数字型(整数型、浮点型和复数…...
民宿酒店订房房态商城小程序的作用是什么
外出旅游出差,酒店民宿总是很好的选择,随着经济复苏,各地旅游及外出办公人次增多,酒店成绩随之增加,市场呈现多品牌酒店经营形式。 区别于以前,如今互联网深入各个行业,酒店经营也面临着困境。…...

acwing算法基础之数据结构--栈和队列
目录 1 知识点2 模板 1 知识点 栈:先进后出。先进的就是栈底,后进的就是栈顶。后进先出嘛,所以在栈顶弹出元素。 队列:先进先出。先进的就是队头,后进的就是队尾。先进先出嘛,所以在队头弹出元素。 单调…...

关于导出的Excel文件的本质
上篇文章中提到关于xlsx改造冻结窗格的代码,我是怎么知道要加pane的呢,加下来就把我的心路历程记录一下。 我改造之前也是没有头绪的,我网上查了很多,只告诉我如何使用,但源码里没有针对!freeze的处理,所以…...

Rust中FnOnce如何传递给一个约束Fn的回调
Rust中FnOnce如何传递给一个约束Fn的回调 下面的代码,set_cb(func);会报错,如何包装能够做到这样的效果: fn set_cb<F: Fn() static>(handler: F) {handler(); }fn main() {let join_handle std::thread::spawn(|| {});let func |…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

项目进度管理软件是什么?项目进度管理软件有哪些核心功能?
无论是建筑施工、软件开发,还是市场营销活动,项目往往涉及多个团队、大量资源和严格的时间表。如果没有一个系统化的工具来跟踪和管理这些元素,项目很容易陷入混乱,导致进度延误、成本超支,甚至失败。 项目进度管理软…...
:PyQuery 框架)
Python爬虫(四):PyQuery 框架
PyQuery 框架详解与对比 BeautifulSoup 第一部分:PyQuery 框架介绍 1. PyQuery 是什么? PyQuery 是一个 Python 的 HTML/XML 解析库,它采用了 jQuery 的语法风格,让开发者能够用类似前端 jQuery 的方式处理文档解析。它的核心特…...

关于 ffmpeg设置摄像头报错“Could not set video options” 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/148515355 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...
