图论-最短路径算法-弗洛伊德算法与迪杰斯特拉算法
弗洛伊德算法:
弗洛伊德算法本质是动态规划,通过添加点进如可选择的点组成的集合的同时更新所有点之间的距离,从而得到每两个点之间的最短距离。
-
初始化: 创建一个二维数组
dist,其中dist[i][j]表示从节点i到节点j的最短路径的权重。将对角线上的元素初始化为0,表示节点到自身的距离。如果存在直接相连的边,则将dist[i][j]初始化为这些边的权重;否则,初始化为一个大数表示无穷大。 -
三重循环: 对于每一对节点
(i, j),以及所有可能的中间节点k,进行三重循环:plaintextCopy code
for k from 1 to n: for i from 1 to n: for j from 1 to n: dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])在每一次迭代中,检查是否通过中间节点
k能够获得更短的路径。如果dist[i][k] + dist[k][j]小于当前已知的dist[i][j],则更新dist[i][j]。 -
输出结果: 算法结束后,矩阵
dist中的元素即为图中所有节点对之间的最短路径。
迪杰斯特拉算法:
迪杰斯特拉算法是广度优先遍历算法的一种,遍历当前节点的所有邻接点,更新原点到邻接点的距离。最终得到原点到每个点的最小距离。
-
初始化: 创建两个数组,
distance和visited。distance数组用于存储从起始节点到各个节点的当前最短路径长度,初始时将起始节点到自身的距离设置为0,其他节点的距离设置为无穷大。visited数组用于标记节点是否已经被访问,初始时所有节点都未被访问。 -
选择起始节点: 将起始节点标记为当前的工作节点。
-
更新邻接节点的距离: 遍历当前工作节点的所有邻接节点,计算从起始节点经过当前工作节点到邻接节点的路径长度。如果这个路径长度小于
distance数组中记录的邻接节点的当前最短路径长度,则更新distance数组。 -
选择下一个工作节点: 从未访问的节点中选择一个具有最小最短路径长度的节点,将其标记为当前的工作节点。如果所有未访问的节点都具有无穷大的最短路径长度,说明剩下的节点不可达,算法结束。
-
重复步骤3和4: 重复执行步骤3和步骤4,直到所有节点都被访问过。
案例题目
现在小丽在城镇A,小明在城镇B。小丽要出发找小明。
城镇之间有双向通行的道路,通过道路要消耗一定的时间。
其中已知城镇C和城镇D之间有双向的传送门,可以不消耗时间瞬间传送过去
现在请你求出小丽从城镇A抵达城镇B的最短时间。保证从起点到终点有路径可达。
输入描述
第一行两个正整数n,m,以空格分开,表示总共有n个城镇,有m条道路相连
第二行两个正整数A,B,以空格分开,分别表示小丽所在城镇A,小明所在城镇B。
第三行两个正整数C,D,以空格分开,表示城镇C和城镇D之间有瞬间的双向传送门。
接下来m行,每行三个正整数u,v, c,以空格分开,表示城镇u和城镇v之间有道路,通过道路消耗时间c。
对于100%的数据保证 1<=n <=100,1<=m<=2*n,每条道路的时间花费在[1,10]之间
输出描述
一行,一个整教表示最短到达时间。
样例输入
4 3
1 4
1 3
1 2 1
2 3 1
2 4 1
样例输出
2代码
弗洛伊德算法
n,m = map(int,input().split(" "))
A,B = map(int,input().split(" "))
print(A,B)
C,D = map(int,input().split(" "))
dis = [[float('inf') for i in range(n+1)] for j in range(n+1)]
for i in range(m):u,v,c = map(int,input().split(" "))dis[u][v] = cdis[v][u] = cdis[C][D] = dis[D][C] = 0for k in range(1,n+1):for i in range(1,n+1):for j in range(1,n+1):dis[i][j] = min(dis[i][j],dis[i][k]+dis[k][j])print(dis[A][B])迪杰斯特拉算法
import collectionsn,m = map(int,input().split(" "))
A,B = map(int,input().split(" "))
C,D = map(int,input().split(" "))graph = [[] for _ in range(n)]
for i in range(m):u,v,c = map(int,input().split(" "))graph[u-1].append((v-1,c))graph[v- 1].append((u-1,c))graph[C-1].append((D-1,0))
graph[D-1].append((C-1,0))def dijkstra(graph,start,end):n = len(graph)distances = [float('inf') for i in range(n)]distances[start] = 0queue = collections.deque( [(0,start)])vis = [False] * nwhile queue:current_distance,current_node = queue.popleft();if vis[current_node]:continuevis[current_node] = Truefor neighbor,weight in graph[current_node]:new_distance = current_distance + weightif new_distance < distances[neighbor]:distances[neighbor] = new_distancequeue.append((new_distance,neighbor))return distances[end]print(dijkstra(graph,A-1,B-1))相关文章:

图论-最短路径算法-弗洛伊德算法与迪杰斯特拉算法
弗洛伊德算法: 弗洛伊德算法本质是动态规划,通过添加点进如可选择的点组成的集合的同时更新所有点之间的距离,从而得到每两个点之间的最短距离。 初始化: 创建一个二维数组 dist,其中 dist[i][j] 表示从节点 i 到节点…...

[23] IPDreamer: Appearance-Controllable 3D Object Generation with Image Prompts
pdf Text-to-3D任务中,对3D模型外观的控制不强,本文提出IPDreamer来解决该问题。在NeRF Training阶段,IPDreamer根据文本用ControlNet生成参考图,并将参考图作为Zero 1-to-3的控制条件,用基于Zero 1-to-3的SDS损失生成…...

深入理解React中的useEffect钩子函数
引言: React是一种流行的JavaScript库,它通过组件化和声明式编程的方式简化了前端开发。在React中,一个核心概念是组件的生命周期,其中包含了许多钩子函数,用于管理组件的不同阶段。其中之一就是useEffect钩子函数&…...

数字化时代的财务管理:挑战与机遇
导语:随着数字化技术的不断发展,财务管理正面临着前所未有的挑战和机遇。数字化不仅改变了财务数据的收集、处理和分析方式,还为财务决策提供了更多的依据和方向。本文将探讨数字化时代财务管理的新特点,以及如何利用数字化技术提…...
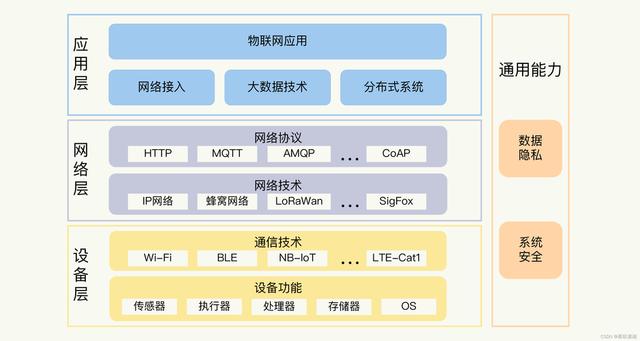
网络通信协议-HTTP、WebSocket、MQTT的比较与应用
在今天的数字化世界中,各种通信协议起着关键的作用,以确保信息的传递和交换。HTTP、WebSocket 和 MQTT 是三种常用的网络通信协议,它们各自适用于不同的应用场景。本文将比较这三种协议,并探讨它们的主要应用领域。 HTTPÿ…...
、dataloader、长短期记忆网络(LSTM)、门控循环单元(GRU)、超参数对比)
【深度学习】深度学习实验四——循环神经网络(RNN)、dataloader、长短期记忆网络(LSTM)、门控循环单元(GRU)、超参数对比
一、实验内容 实验内容包含要进行什么实验,实验的目的是什么,实验用到的算法及其原理的简单介绍。 1.1 循环神经网络 (1)理解序列数据处理方法,补全面向对象编程中的缺失代码,并使用torch自带数据工具将数据封装为dataloader。 (2)分别采用手动方式以及调用接口方式…...

DB2分区表详解
一、分区表基本概念 当表中的数据量不断增大,查询数据的速度就会变慢,应用程序的性能就会下降,这时就应该考虑对表进行分区。分区后的表称为分区表。 表进行分区后,逻辑上表仍然是一张完整的表,只是将表中的数据在物理上存放到多个“表空间”(物理文件上),这样查询数据时…...

基本地址变换机构
基本地址变换机构:用于实现逻辑地址到物理地址转换的一组硬件机构。 关于页号页表的定义,放个本人的传送门 1.页表寄存器 基本地址变换机构可以借助进程的页表将逻辑地址转换为物理地址。 1.作用 通常会在系统中设置一个页表寄存器(PTR&…...
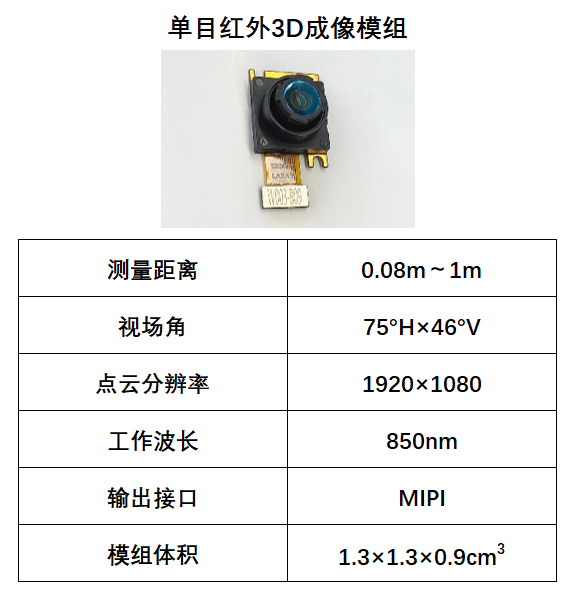
以单颗CMOS摄像头重构三维场景,维悟光子发布单目红外3D成像模组
维悟光子近期发布全新单目红外3D成像模组,现可提供下游用户进行测试导入。通过结合微纳光学元件编码和人工智能算法解码,维悟光子单目红外3D成像模组采用单颗摄像头,通过单帧拍摄,可同时获取像素级配准的3D点云和红外图像信息,可被应用于机器人、生物识别等广阔领域。 市场…...
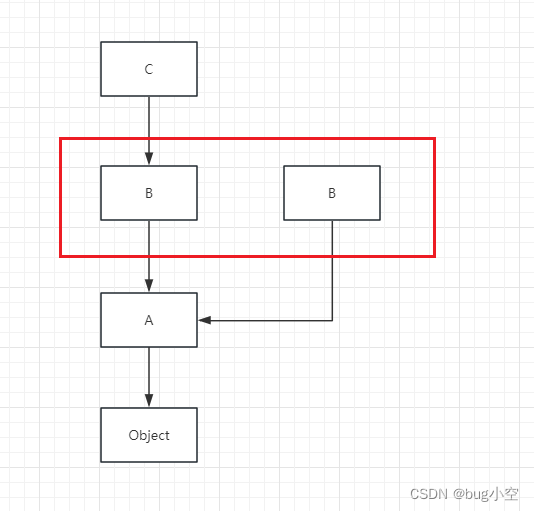
Jinja2模板注入 | python模板注入特殊属性 / 对象讲解
在进行模板利用的时候需要使用特殊的属性和对象进行利用,这里对这些特殊属性及方法进行讲解 以下实验输出python3版本为 3.10.4, python2版本为 2.7.13 特殊属性 __class__ 类实例上使用,它用于获取该实例对应的类__base__ 用于获取父类__mr…...

一致性公式证明
首先,假设存在两个不同的聚类假设 f 1 f^1 f1和 f 2 f^2 f2,它们在两个视角上的聚类结果分别为 y 1 ∈ { − 1 , 1 } n y^1\in\{-1,1\}^n y1∈{−1,1}n和 y 2 ∈ { − 1 , 1 } n y^2\in\{-1,1\}^n y2∈{−1,1}n。 证明一致性不等式: …...
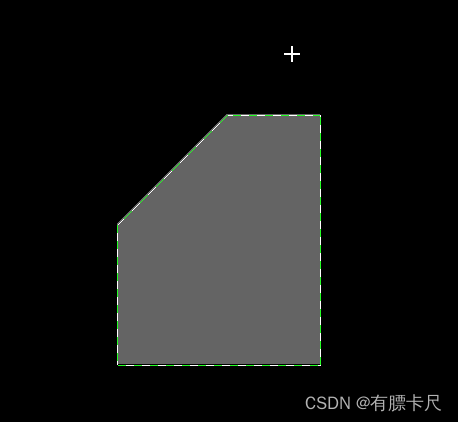
allegro中shape的一些基本操作(一)——添加和修改shape
添加shape 简单添加shape的方式有3种,如下图所示 点击选择相应的shape模式后可以在option面板中设置相应的shape参数(这里不做过多介绍,里面可以设置shape的大小、静态或动态shape等参数),然后再用鼠标在相应的层上添…...
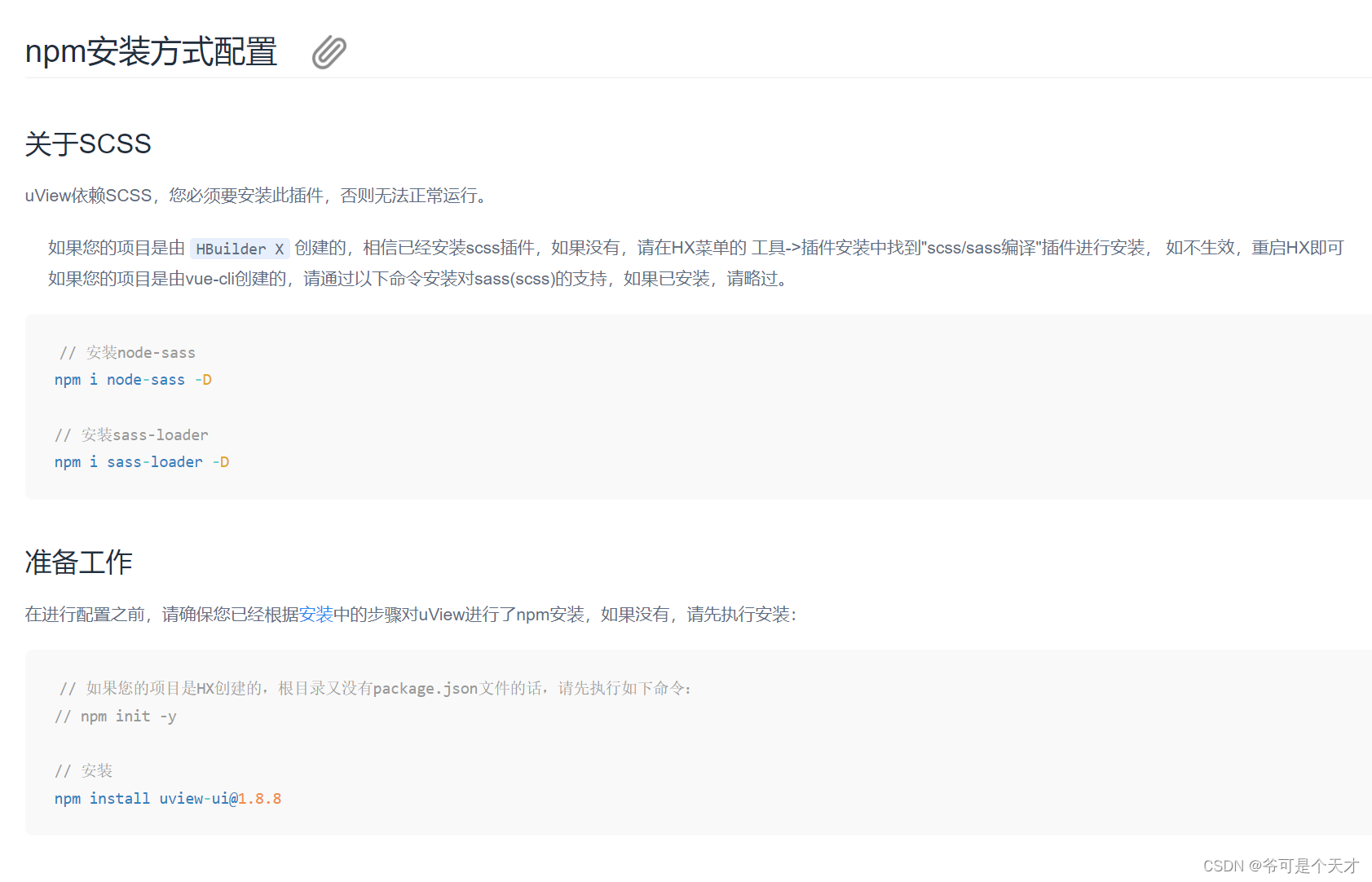
HBuilder创建uniapp默认项目导入uview(胎教)
1:更新HBuilder 建议更新 2:更新插件 我本人在没有更新插件的情况下报错了,找到了**这个大佬**解决问题,所以建议更新插件 先卸载uni-app(Vue2)编译 再重新安装 uni-app(Vue2)…...

C语言基础算法复习
003 斐波那契数列问题 #include<stdio.h> int main() {int i,f11,f21,f3,num;printf("%5d %5d",f1,f2);num2;for(i1; i<18; i){f3f1f2;f1f2;f2f3;num;printf("%5d",f3);if(num%40) printf("\n");}return 0; }//#输数斐波那契数列的前20…...
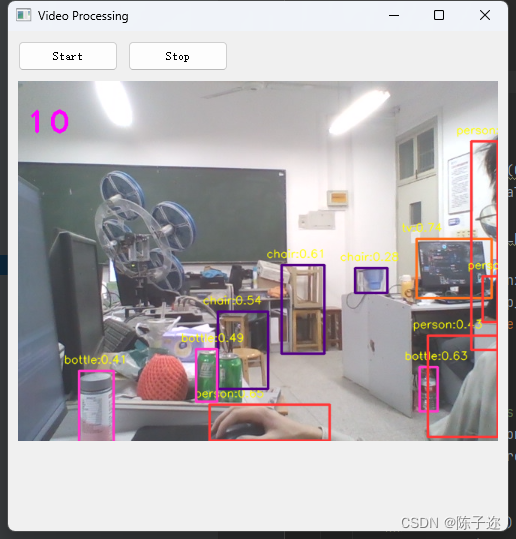
PyQt界面里如何加载本地视频以及调用摄像头实时检测(小白入门必看)
目录 1.PyQt介绍 2.代码实现 2.1实时调用摄像头 2.2 使用YOLOv5推理 2.3 代码中用到的主要函数 1.PyQt介绍 PyQt是一个用于创建桌面应用程序的Python绑定库,它基于Qt框架。Qt是一个跨平台的C应用程序开发框架,提供了丰富的图形界面、网络通信、数据…...
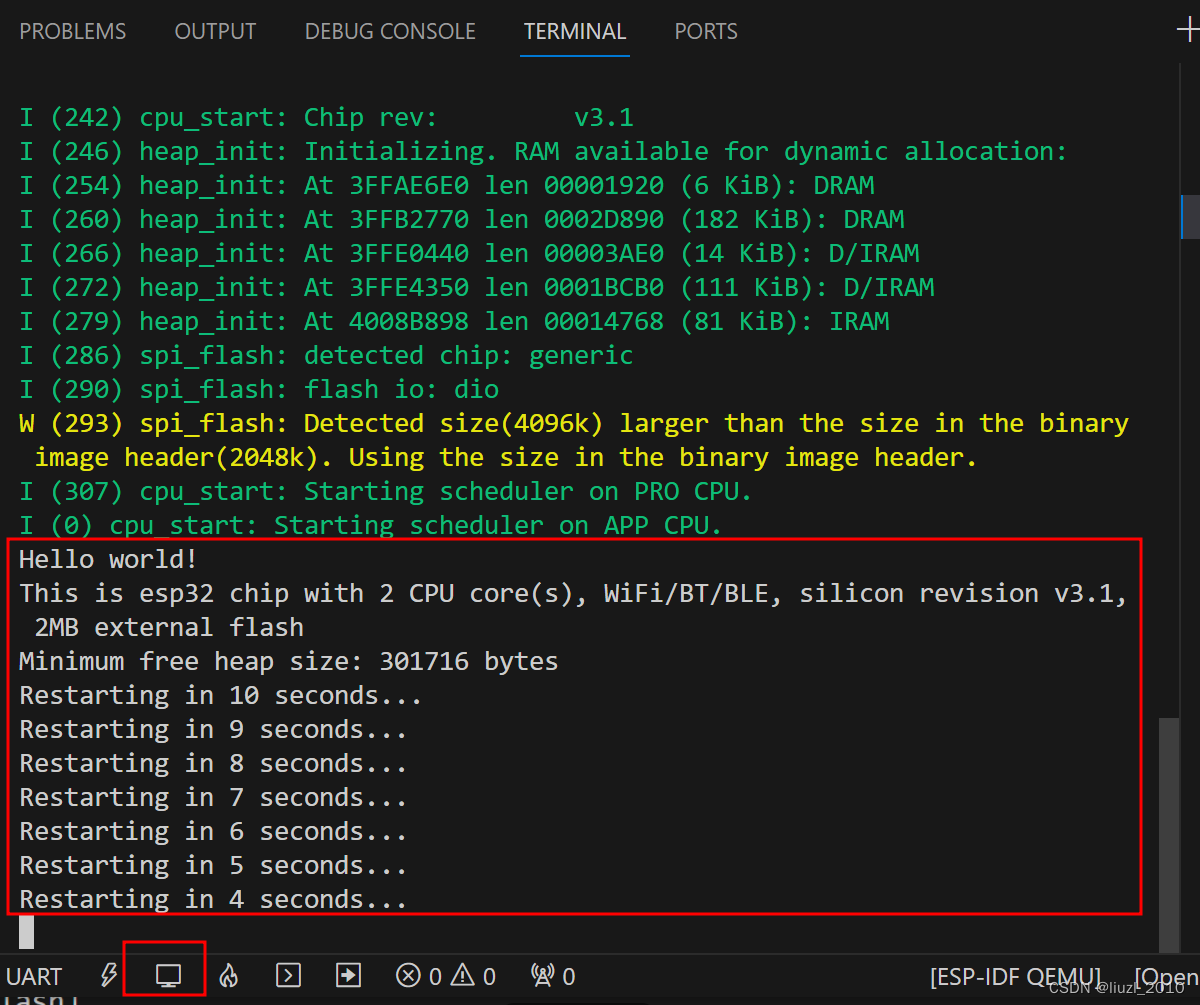
Ubuntu:VS Code IDE安装ESP-IDF【保姆级】
物联网开发学习笔记——目录索引 参考: VS Code官网:Visual Studio Code - Code Editing. Redefined 乐鑫官网:ESP-IDF 编程指南 - ESP32 VSCode ESP-ID Extension Install 一、前提条件 Visual Studio Code IDE安装ESP-IDF扩展&…...

软考高级系统架构设计师系列之:快速掌握软件工程核心知识点
软考高级系统架构设计师系列之:快速掌握软件工程核心知识点 一、软件开发方法二、软件开发模型三、软件开发模型-瀑布模型四、软件开发模型-经典模型汇总五、软件开发模型-增量模型与螺旋模型六、软件开发模型-V模型七、软件开发模型-构件组装模型八、软件开发模型-统一过程九…...

Java基础面试-ArrayList和LinkedList的区别
ArrayList: 基于动态数组,连续内存存储,适合下标访问(随机访问),扩容机制: 因为数组长度固定,超出长度存数据时需要新建数组,然后将老数组的数据拷贝到新数组,如果不是尾部插入数据还会涉及到元素的移动(往…...

如何从 Pod 内访问 Kubernetes 集群的 API
Kubernetes API 是您检查和管理集群操作的途径。您可以使用Kubectl CLI、工具(例如curl)或流行编程语言的官方集成库来使用 API 。 该 API 也可供集群内的应用程序使用。Kubernetes Pod 会自动获得对 API 的访问权限,并且可以使用提供的服务帐户进行身份验证。您可以通过使…...

计网面试复习自用
五层: 应用层:应用层是最高层,负责为用户提供网络服务和应用程序。在应用层,用户应用程序与网络进行交互,发送和接收数据。典型的应用层协议包括HTTP(用于网页浏览)、SMTP(用于电子邮…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...
