MySQL为什么用b+树
索引是一种数据结构,用于帮助我们在大量数据中快速定位到我们想要查找的数据。 索引最形象的比喻就是图书的目录了。注意这里的大量,数据量大了索引才显得有意义,如果我想要在[1,2,3,4]中找到4这个数据,直接对全数据检索也很快,没有必要费力气建索引再去查找。索引在mysql数据库中分三类:
B+树索引、Hash索引、全文索引
我们今天要介绍的是工作开发中最常接触到innodb存储引擎中的的B+树索引。
要介绍B+树索引,就不得不提二叉查找树,平衡二叉树和B树这三种数据结构。B+树就是从他们仨演化来的。
二叉查找树
首先,让我们先看一张图

从图中可以看到,我们为user表(用户信息表)建立了一个二叉查找树的索引。图中的圆为二叉查找树的节点,节点中存储了键(key)和数据(data)。
键对应user表中的id,数据对应user表中的行数据。二叉查找树的特点就是任何节点的左子节点的键值都小于当前节点的键值,右子节点的键值都大于当前节点的键值。 顶端的节点我们称为根节点,没有子节点的节点我们称之为叶节点。
如果我们需要查找id=12的用户信息,利用我们创建的二叉查找树索引,查找流程如下:
-
\1. 将根节点作为当前节点,把12与当前节点的键值10比较,12大于10,接下来我们把当前节点>的右子节点作为当前节点。
-
\2. 继续把12和当前节点的键值13比较,发现12小于13,把当前节点的左子节点作为当前节点。
-
\3. 把12和当前节点的键值12对比,12等于12,满足条件,我们从当前节点中取出data,即id=12,name=xm。
利用二叉查找树我们只需要3次即可找到匹配的数据。如果在表中一条条的查找的话,我们需要6次才能找到。
平衡二叉树
上面我们讲解了利用二叉查找树可以快速的找到数据。但是,如果上面的二叉查找树是这样的构造:
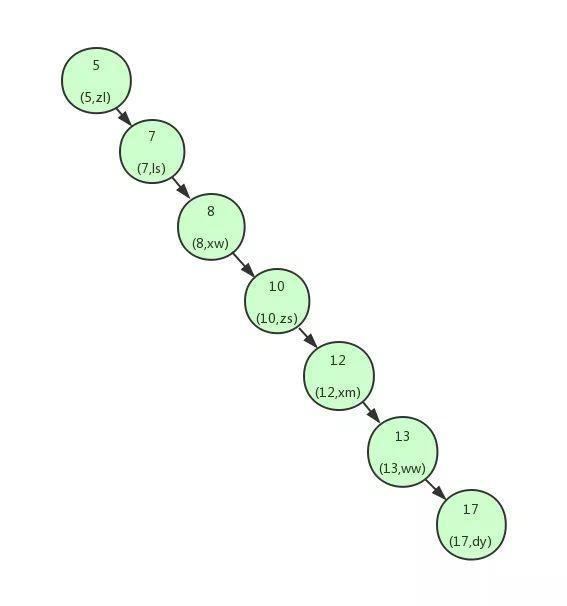
这个时候可以看到我们的二叉查找树变成了一个链表。
如果我们需要查找id=17的用户信息,我们需要查找7次,也就相当于全表扫描了。
导致这个现象的原因其实是二叉查找树变得不平衡了,也就是高度太高了,从而导致查找效率的不稳定。
为了解决这个问题,我们需要保证二叉查找树一直保持平衡,就需要用到平衡二叉树了。
平衡二叉树又称AVL树,在满足二叉查找树特性的基础上,要求每个节点的左右子树的高度差不能超过1。
下面是平衡二叉树和非平衡二叉树的对比:
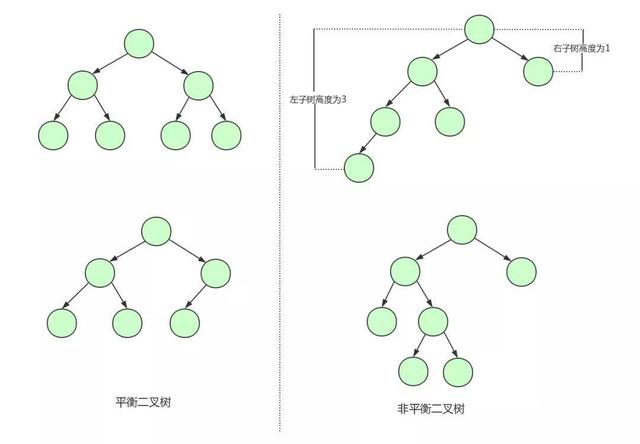
由平衡二叉树的构造我们可以发现第一张图中的二叉树其实就是一棵平衡二叉树。
平衡二叉树保证了树的构造是平衡的,当我们插入或删除数据导致不满足平衡二叉树不平衡时,平衡二叉树会进行调整树上的节点来保持平衡。具体的调整方式这里就不介绍了。
平衡二叉树相比于二叉查找树来说,查找效率更稳定,总体的查找速度也更快。
B树
因为内存的易失性。一般情况下,我们都会选择将user表中的数据和索引存储在磁盘这种外围设备中。
但是和内存相比,从磁盘中读取数据的速度会慢上百倍千倍甚至万倍,所以,我们应当尽量减少从磁盘中读取数据的次数。 另外,从磁盘中读取数据时,都是按照磁盘块来读取的,并不是一条一条的读。
如果我们能把尽量多的数据放进磁盘块中,那一次磁盘读取操作就会读取更多数据,那我们查找数据的时间也会大幅度降低。
如果我们用树这种数据结构作为索引的数据结构,那我们每查找一次数据就需要从磁盘中读取一个节点,也就是我们说的一个磁盘块,我们都知道平衡二叉树可是每个节点只存储一个键值和数据的。
那说明什么?
说明每个磁盘块仅仅存储一个键值和数据!
那如果我们要存储海量的数据呢?
可以想象到二叉树的节点将会非常多,高度也会及其高,我们查找数据时也会进行很多次磁盘IO,我们查找数据的效率将会极低!
为了解决平衡二叉树的这个弊端,我们应该寻找一种单个节点可以存储多个键值和数据的平衡树。也就是我们接下来要说的B树。
B树(Balance Tree)即为平衡树的意思,下图即是一颗B树。
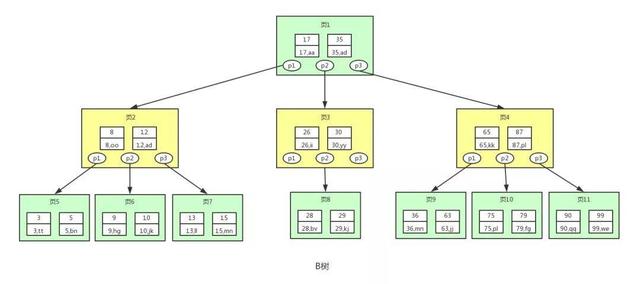
图中的p节点为指向子节点的指针,二叉查找树和平衡二叉树其实也有,因为图的美观性,被省略了。- 图中的每个节点称为页,页就是我们上面说的磁盘块,在mysql中数据读取的基本单位都是页,所以我们这里叫做页更符合mysql中索引的底层数据结构。
从上图可以看出,B树相对于平衡二叉树,每个节点存储了更多的键值(key)和数据(data),并且每个节点拥有更多的子节点,子节点的个数一般称为阶,上述图中的B树为3阶B树,高度也会很低。
基于这个特性,B树查找数据读取磁盘的次数将会很少,数据的查找效率也会比平衡二叉树高很多。
假如我们要查找id=28的用户信息,那么我们在上图B树中查找的流程如下:
-
\1. 先找到根节点也就是页1,判断28在键值17和35之间,我们那么我们根据页1中的指针p2找到页3。
-
\2. 将28和页3中的键值相比较,28在26和30之间,我们根据页3中的指针p2找到页8。
-
\3. 将28和页8中的键值相比较,发现有匹配的键值28,键值28对应的用户信息为(28,bv)。
B+树
B+树是对B树的进一步优化。让我们先来看下B+树的结构图:
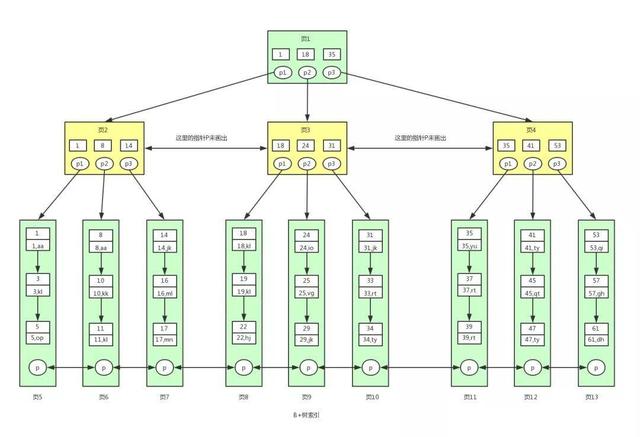
根据上图我们来看下B+树和B树有什么不同。
\1. B+树非叶子节点上是不存储数据的,仅存储键值,而B树节点中不仅存储键值,也会存储数据。之所以这么做是因为在数据库中页的大小是固定的,innodb中页的默认大小是16KB。如果不存储数据,那么就会存储更多的键值,相应的树的阶数(节点的子节点树)就会更大,树就会更矮更胖,如此一来我们查找数据进行磁盘的IO次数有会再次减少,数据查询的效率也会更快。另外,B+树的阶数是等于键值的数量的,如果我们的B+树一个节点可以存储1000个键值,那么3层B+树可以存储1000×1000×1000=10亿个数据。一般根节点是常驻内存的,所以一般我们查找10亿数据,只需要2次磁盘IO。
\2. 因为B+树索引的所有数据均存储在叶子节点,而且数据是按照顺序排列的。那么B+树使得范围查找,排序查找,分组查找以及去重查找变得异常简单。而B树因为数据分散在各个节点,要实现这一点是很不容易的。
有心的读者可能还发现上图B+树中各个页之间是通过双向链表连接的,叶子节点中的数据是通过单向链表连接的。
其实上面的B树我们也可以对各个节点加上链表。其实这些不是它们之前的区别,是因为在mysql的innodb存储引擎中,索引就是这样存储的。也就是说上图中的B+树索引就是innodb中B+树索引真正的实现方式,准确的说应该是聚集索引(聚集索引和非聚集索引下面会讲到)。
通过上图可以看到,在innodb中,我们通过数据页之间通过双向链表连接以及叶子节点中数据之间通过单向链表连接的方式可以找到表中所有的数据。
MyISAM中的B+树索引实现与innodb中的略有不同。在MyISAM中,B+树索引的叶子节点并不存储数据,而是存储数据的文件地址。
聚集索引 VS 非聚集索引
在上节介绍B+树索引的时候,我们提到了图中的索引其实是聚集索引的实现方式。那什么是聚集索引呢?
在MySQL中,B+树索引按照存储方式的不同分为聚集索引和非聚集索引。
这里我们着重介绍innodb中的聚集索引和非聚集索引。
\1. 聚集索引(聚簇索引):以innodb作为存储引擎的表,表中的数据都会有一个主键,即使你不创建主键,系统也会帮你创建一个隐式的主键。这是因为innodb是把数据存放在B+树中的,而B+树的键值就是主键,在B+树的叶子节点中,存储了表中所有的数据。这种以主键作为B+树索引的键值而构建的B+树索引,我们称之为聚集索引。
\2. 非聚集索引(非聚簇索引):以主键以外的列值作为键值构建的B+树索引,我们称之为非聚集索引。非聚集索引与聚集索引的区别在于非聚集索引的叶子节点不存储表中的数据,而是存储该列对应的主键,想要查找数据我们还需要根据主键再去聚集索引中进行查找,这个再根据聚集索引查找数据的过程,我们称为回表。
明白了聚集索引和非聚集索引的定义,我们应该明白这样一句话:数据即索引,索引即数据。
利用聚集索引和非聚集索引查找数据
前面我们讲解B+树索引的时候并没有去说怎么在B+树中进行数据的查找,主要就是因为还没有引出聚集索引和非聚集索引的概念。下面我们通过讲解如何通过聚集索引以及非聚集索引查找数据表中数据的方式介绍一下B+树索引查找数据方法。
利用聚集索引查找数据
还是这张B+树索引图,现在我们应该知道这就是聚集索引,表中的数据存储在其中。现在假设我们要查找id>=18并且id<40的用户数据。对应的sql语句为select * from user where id>=18 and id <40,其中id为主键。具体的查找过程如下:
-
\1. 一般根节点都是常驻内存的,也就是说页1已经在内存中了,此时不需要到磁盘中读取数据,直接从内存中读取即可。
从内存中读取到页1,要查找这个id>=18 and id <40或者范围值,我们首先需要找到id=18的键值。
从页1中我们可以找到键值18,此时我们需要根据指针p2,定位到页3。
-
\2. 要从页3中查找数据,我们就需要拿着p2指针去磁盘中进行读取页3。
从磁盘中读取页3后将页3放入内存中,然后进行查找,我们可以找到键值18,然后再拿到页3中的指针p1,定位到页8。
-
\3. 同样的页8页不在内存中,我们需要再去磁盘中将页8读取到内存中。
将页8读取到内存中后。
因为页中的数据是链表进行连接的,而且键值是按照顺序存放的,此时可以根据二分查找法定位到键值18。
此时因为已经到数据页了,此时我们已经找到一条满足条件的数据了,就是键值18对应的数据。
因为是范围查找,而且此时所有的数据又都存在叶子节点,并且是有序排列的,那么我们就可以对页8中的键值依次进行遍历查找并匹配满足条件的数据。
我们可以一直找到键值为22的数据,然后页8中就没有数据了,此时我们需要拿着页8中的p指针去读取页9中的数据。
-
\4. 因为页9不在内存中,就又会加载页9到内存中,并通过和页8中一样的方式进行数据的查找,直到将页12加载到内存中,发现41大于40,此时不满足条件。
那么查找到此终止。
最终我们找到满足条件的所有数据为:
(18,kl),(19,kl),(22,hj),(24,io),(25,vg),(29,jk),(31,jk),(33,rt),(34,ty),(35,yu),(37,rt),(39,rt)。
总共12条记录。
下面看下具体的查找流程图:

利用非聚集索引查找数据

读者看到这张图的时候可能会蒙,这是啥东西啊?怎么都是数字。
如果有这种感觉,请仔细看下图中红字的解释。什么?还看不懂?那我再来解释下吧。首先,这个非聚集索引表示的是用户幸运数字的索引(为什么是幸运数字?一时兴起想起来的:-)),此时表结构是这样的。
在叶子节点中,不在存储所有的数据了,存储的是键值和主键。
对于叶子节点中的x-y,比如1-1。左边的1表示的是索引的键值,右边的1表示的是主键值。如果我们要找到幸运数字为33的用户信息,对应的sql语句为select * from user where luckNum=33。
查找的流程跟聚集索引一样,这里就不详细介绍了。我们最终会找到主键值47,找到主键后我们需要再到聚集索引中查找具体对应的数据信息,此时又回到了聚集索引的查找流程。

在MyISAM中,聚集索引和非聚集索引的叶子节点都会存储数据的文件地址。
相关文章:

MySQL为什么用b+树
索引是一种数据结构,用于帮助我们在大量数据中快速定位到我们想要查找的数据。 索引最形象的比喻就是图书的目录了。注意这里的大量,数据量大了索引才显得有意义,如果我想要在[1,2,3,4]中找到4这个数据,直接对全数据检索也很快&am…...

浅谈机器学习中的概率模型
浅谈机器学习中的概率模型 其实,当牵扯到概率的时候,一切问题都会变的及其复杂,比如我们监督学习任务中,对于一个分类任务,我们经常是在解决这样一个问题,比如对于一个n维的样本 X [ x 1 , x 2 , . . . .…...

MySQL 函数 索引 事务 管理
目录 一. 字符串相关的函数 二.数学相关函数 编辑 三.时间日期相关函数 date.sql 四.流程控制函数 centrol.sql 分页查询 使用分组函数和分组字句 group by 数据分组的总结 多表查询 自连接 子查询 subquery.sql 五.表的复制 六.合并查询 七.表的外连接 …...

Flink如何基于事件时间消费分区数比算子并行度大的kafka主题
背景 使用flink消费kafka的主题的情况我们经常遇到,通常我们都是不需要感知数据源算子的并行度和kafka主题的并行度之间的关系的,但是其实在kafka的主题分区数大于数据源算子的并行度时,是有一些注意事项的,本文就来讲解下这些注…...
总结:JavaEE的Servlet中HttpServletRequest请求对象调用各种API方法结果示例
总结:JavaEE的Servlet中HttpServletRequest请求对象调用各种API方法结果示例 一方法调用顺序是按照英文字母顺序从A-Z二该示例可以用作servlet中request的API参考,从而知道该如何获取哪些路径参数等等三Servlet的API版本5.0.0、JSP的API版本:…...
ChatGPT AIGC 完成Excel跨多表查找操作vlookup+indirect
VLOOKUP和INDIRECT的组合在Excel中用于跨表查询,其中VLOOKUP函数用于在另一张表中查找数据,INDIRECT函数则用于根据文本字符串引用不同的工作表。具体操作如下: 1.假设在工作表1中,A列有你要查找的值,B列是你希望查询的工作表名称。 2.在工作表1的C列输入以下公式:=VLO…...

Linux系统conda虚拟环境离线迁移移植
本人创建的conda虚拟环境名为yys(每个人的虚拟环境名不一样,替换下就行) 以下为迁移步骤: 1.安装打包工具将虚拟环境打包: conda install conda-pack conda pack -n yys -o yys.tar.gz 2.将yys.tar.gz上传到服务器&…...

Vue16 绑定css样式 style样式
绑定样式: 1. class样式写法:class"xxx" xxx可以是字符串、对象、数组。字符串写法适用于:类名不确定,要动态获取。对象写法适用于:要绑定多个样式,个数不确定,名字也不确定。数组写法适用于&…...
[Spring] SpringMVC 简介(三)
目录 九、SpringMVC 中的 AJAX 请求 1、简单示例 2、RequestBody(重点关注“赋值形式”) 3、ResponseBody(经常用) 4、为什么不用手动接收 JSON 字符串、转换 JSON 字符串 5、RestController 十、文件上传与下载 1、Respo…...

kettle应用-从数据库抽取数据到excel
本文介绍使用kettle从postgresql数据库中抽取数据到excel中。 首先,启动kettle 如果kettle部署在windows系统,双击运行spoon.bat或者在命令行运行spoon.bat 如果kettle部署在linux系统,需要执行如下命令启动 chmod x spoon.sh nohup ./sp…...
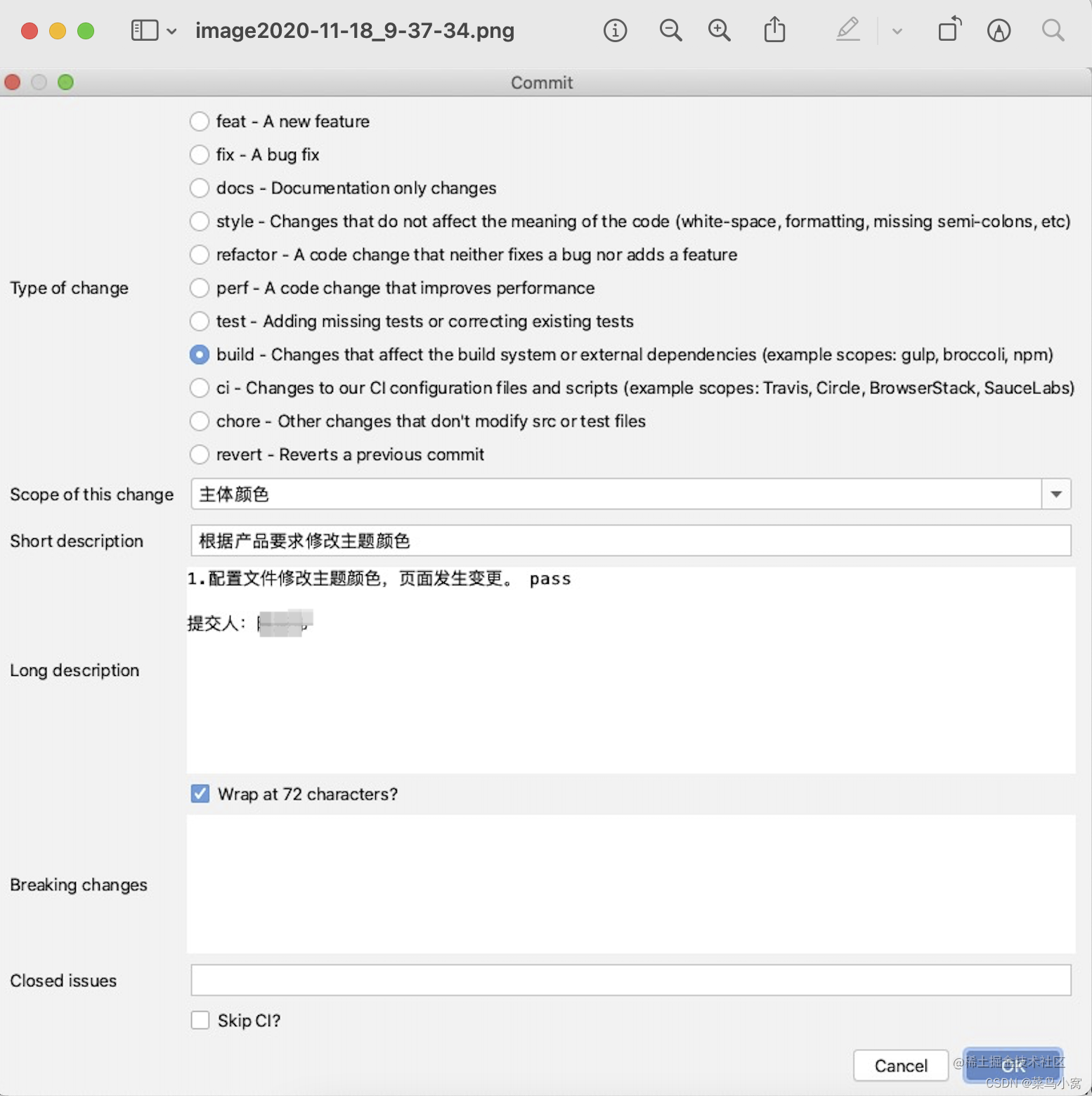
Git Commit Message规范
概述 Git commit message规范是一种良好的实践,可以帮助开发团队更好地理解和维护代码库的历史记录。它可以提高代码质量、可读性和可维护性。下面是一种常见的Git commit message规范,通常被称为"Conventional Commits"规范: 一…...

Linux网络编程系列之UDP广播
Linux网络编程系列 (够吃,管饱) 1、Linux网络编程系列之网络编程基础 2、Linux网络编程系列之TCP协议编程 3、Linux网络编程系列之UDP协议编程 4、Linux网络编程系列之UDP广播 5、Linux网络编程系列之UDP组播 6、Linux网络编程系列之服务器编…...
)
spring中事务相关面试题(自用)
1 什么是spring事务 Spring事务管理的实现原理是基于AOP(面向切面编程)和代理模式。Spring提供了两种主要的方式来管理事务:编程式事务管理和声明式事务管理。 声明式事务管理: Spring的声明式事务管理是通过使用注解或XML配置来…...
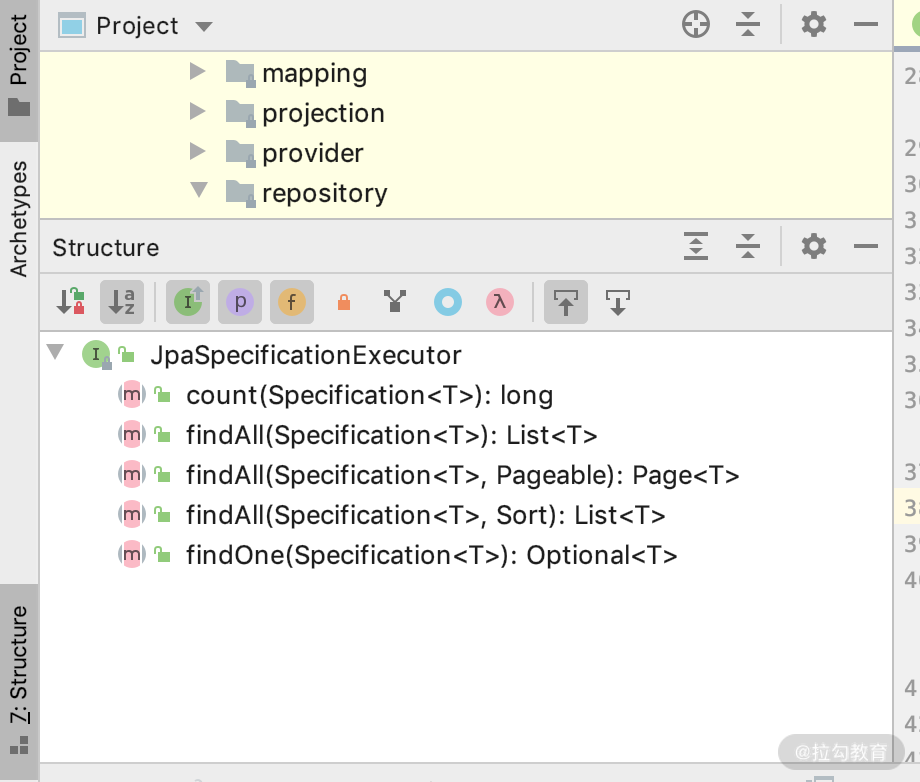
09 | JpaSpecificationExecutor 解决了哪些问题
QueryByExampleExecutor用法 QueryByExampleExecutor(QBE)是一种用户友好的查询技术,具有简单的接口,它允许动态查询创建,并且不需要编写包含字段名称的查询。 下面是一个 UML 图,你可以看到 QueryByExam…...
之su)
Linux命令(93)之su
linux命令之su 1.su介绍 linux命令su用于变更为其它使用者的身份,如root用户外,需要输入使用者的密码 2.su用法 su [参数] user su参数 参数说明-c <command>执行指定的命令,然后切换回原用户-切换到目标用户的环境变量 3.实例 3…...

1.HTML-HTML解决中文乱码问题
题记 下面是html文件解决中文乱码的方法 方法一 在 HTML 文件的 <head> 标签中添加 <meta charset"UTF-8">,确保文件以 UTF-8 编码保存 <head> <meta charset"UTF-8"> <!-- 其他标签和内容 --> </head> --…...

Vue3 + Nodejs 实战 ,文件上传项目--实现拖拽上传
目录 1.拖拽上传的剖析 input的file默认拖动 让其他的盒子成为拖拽对象 2.处理文件的上传 处理数据 上传文件的函数 兼顾点击事件 渲染已处理过的文件 测试效果 3.总结 博客主页:専心_前端,javascript,mysql-CSDN博客 系列专栏:vue3nodejs 实战-…...
Windows:VS Code IDE安装ESP-IDF【保姆级】
物联网开发学习笔记——目录索引 参考: VS Code官网:Visual Studio Code - Code Editing. Redefined 乐鑫官网:ESP-IDF 编程指南 - ESP32 VSCode ESP-ID Extension Install 一、前提条件 Visual Studio Code IDE安装ESP-IDF扩展…...
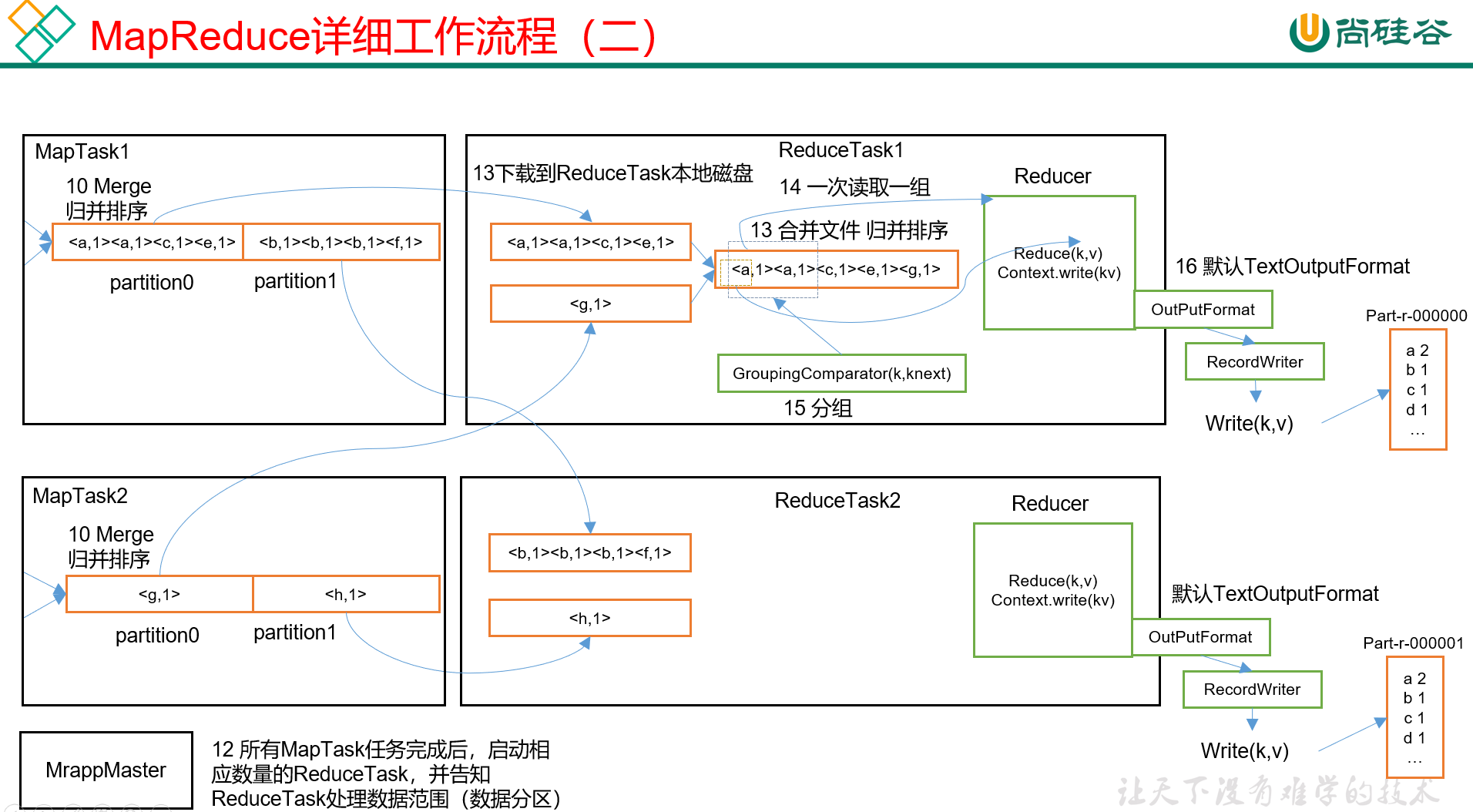
Hadoop3教程(十一):MapReduce的详细工作流程
文章目录 (94)MR工作流程Map阶段Reduce阶段 参考文献 (94)MR工作流程 本小节将展示一下整个MapReduce的全工作流程。 Map阶段 首先是Map阶段: 首先,我们有一个待处理文本文件的集合; 客户端…...

测试中Android与IOS分别关注的点
目录 1、自身不同点 2、测试注重点 3、其他测试点 主要从本身系统的不同点、系统造成的不同点、和注意的测试点做总结 1、自身不同点 研发商:Adroid是google公司做的手机系统,IOS是苹果公司做的手机系统 开源程度:Android是开源的&a…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

服务器硬防的应用场景都有哪些?
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式,避免服务器受到各种恶意攻击和网络威胁,那么,服务器硬防通常都会应用在哪些场景当中呢? 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...
