数据结构-----红黑树简介
目录
前言
1.什么是红黑树?
2.为什么需要红黑树?(与AVL树对比)
3.红黑树的特性
前言
在此之前我们学习过了二叉排序树和平衡二叉树(AVL树),这两种树都是属于搜索树的一种,那么今天我们就开始学习一种新的搜索树,即红黑树,可能在接触二叉树学习的时候我们就听说过了红黑树,当然我们也知道,红黑树相较于前面所学的数据结构(链表、栈、队列、堆……)都难上了很多倍,那么这一期我就来初步的介绍红黑树的相关特性和其知识点,后面我会详细发布关于红黑树的文章来进一步介绍红黑树的操作和代码实现,废话不多说,开始今天的学习吧!
相关链接:
二叉排序树:数据结构-----二叉排序树_Gretel Tade的博客-CSDN博客
AVL树:数据结构-----平衡二叉树_Gretel Tade的博客-CSDN博客
1.什么是红黑树?
红黑树是一种自平衡的二叉查找树,是一种高效的查找树。它是由 Rudolf Bayer 于1972年发明,在当时被称为对称二叉 B 树(symmetric binary B-trees)。后来,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。
红黑树如图所示: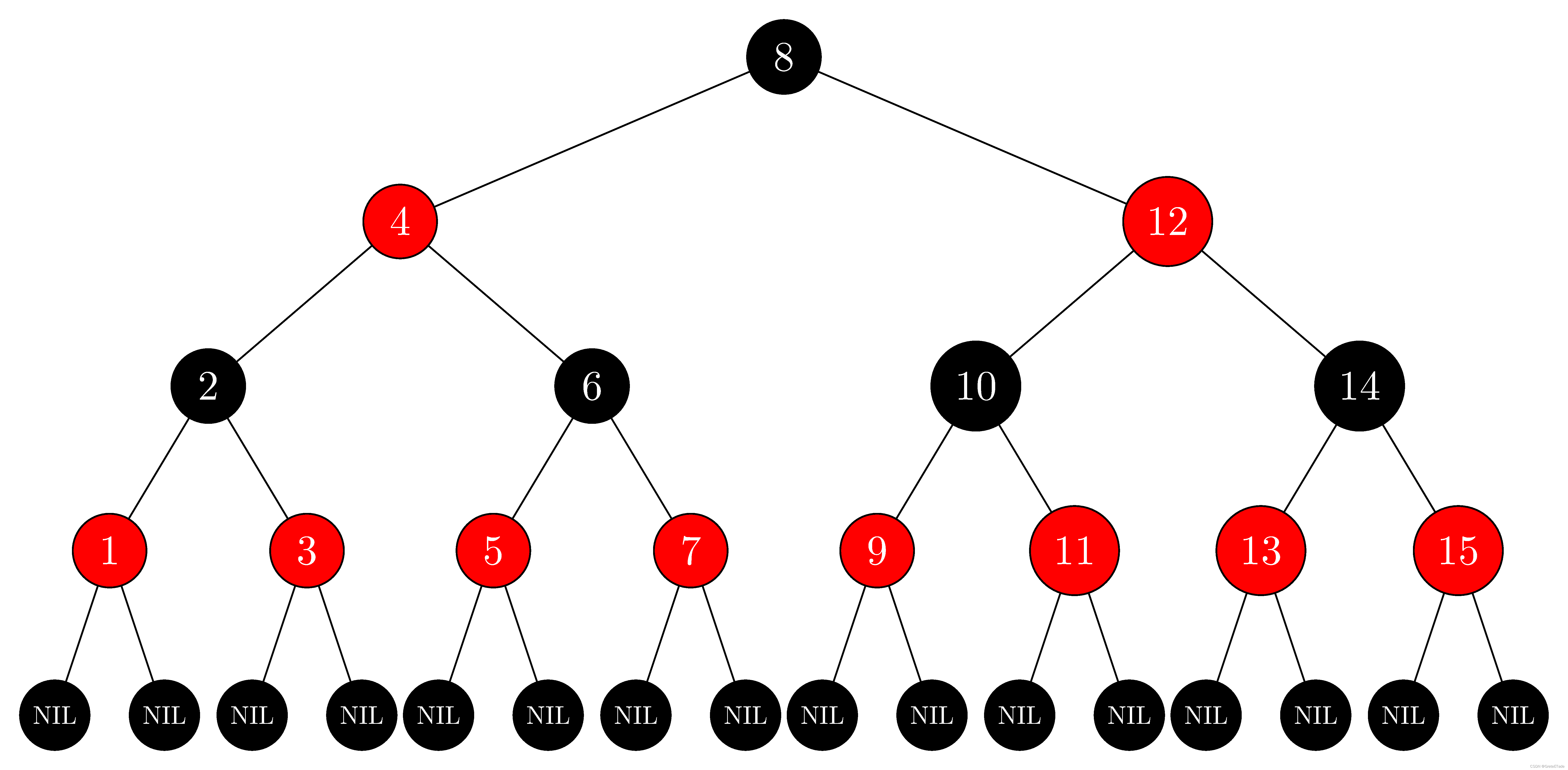
2.为什么需要红黑树?(与AVL树对比)
在此之前我们学习了AVL树,既然AVL树有了高效率的查找功能,那需要红黑树干什么呢?下面看对比就知道了。
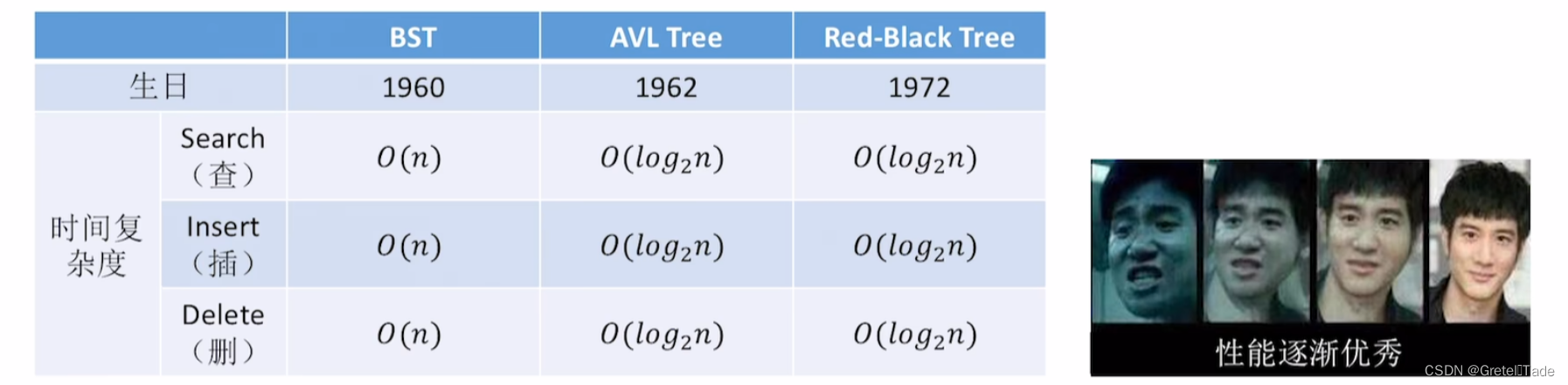
红黑树(Red-Black Tree)和AVL树(Adelson-Velsky and Landis Tree)都是自平衡二叉搜索树,用于在动态数据集上进行高效的插入、删除和搜索操作。它们之间有一些相似之处,但也存在一些关键的区别。如下所示:
平衡性比较:
AVL树:平衡二叉树是一种绝对平衡的二叉树,其满足每个节点的左右子树的高度只差不超过1,所以其在查找方面上是非常迅捷的,但是在插入和删除操作的时候要不断去旋转来满足平衡条件。
红黑树:红黑树是一种弱平衡的二叉树,其不需要像AVL树那样满足左右子树高度差不超过1,红黑树树的高度最多是2倍的对数级别,所以红黑树的插入和删除操作方面更具有灵活性,但是有一些方面性能还是不如AVL树的。
插入和删除性能比较:
AVL树:AVL树在插入和删除过程中必须满足绝对平衡,所以要频繁的进行旋转操作,时间复杂度比较大
红黑树:红黑树是满足弱平衡状态,有红黑两种颜色去控制树的结构,在插入和删除过程中不需要多次旋转操作,这方面是优于平衡二叉树的。
操作效率比较:
AVL树:平衡二叉树满足绝对平衡,其查找效率绝对是最快的,时间复杂度为 O(logn).
红黑树:虽然红黑树的查找时间复杂度也是O(logn),但是相较于平衡二叉树,操作速度是要慢一些的。

对比总结
AVL树:适合应用于搜索场景,以查为主。
红黑树:适合用于频繁插入、删除场景,其实用性更加强。
总的来说各有各的特色吧,现实生活和工作中用的比较多的方面那肯定是红黑树的了,所以学好红黑树很重要!!!
红黑树的相关应用场景:
红黑树具有良好的效率,它可在 O(logN) 时间内完成查找、增加、删除等操作。因此,红黑树在业界应用很广泛,比如 Java 中的 TreeMap,JDK 1.8 中的 HashMap、C++ STL 中的 map 均是基于红黑树结构实现的。
3.红黑树的特性
既然知道了红黑树的优秀,多余的就不多说了,所以这里就开始学习红黑树的知识点了,首先先了解红黑树的特性,需要什么条件才可以满足红黑树。
对于一个红黑树必须满足以下的6个特性:
1.红黑树是一个二叉排序树
2.每个节点要么是红色,要么是黑色
3.根结点是黑色的
4.叶子节点(外部节点,NULL节点、失败的节点)都是黑色的
5.红色节点的父节点和子节点都是黑色的(不存在两个相邻的红色节点)
6.对于每一个节点,从该节点到任一叶子结点的路径上,其所含黑色节点的数量相同
红黑树上面这6条性质可能对于有些人不太好记住或者记错,别急,我下面送各位一个顺口溜,保证你们看了就懂:

顺口溜解释:
左根右:表示红黑树满足 左子节点<根节点<右子节点,也就是满足排序条件
根叶黑:表示跟节点和叶子节点都是黑色的
不红红:表示不能有两个连续的红色节点(父节点和子节点不可能同时是红色的)
黑路同:表示从任意应该节点走到子节点路径上的黑色节点数量是相同的
记住了这个顺口溜就等于记住了红黑树的特性,是不是很简单呢?来下面看几个简单的判断是否为红黑树的示例:
示例1:
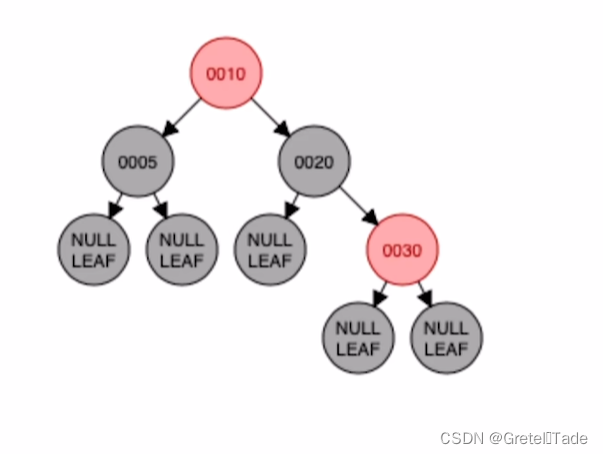
很明显这个不是红黑树,为什么呢?没有排序啊!!!
示例2:
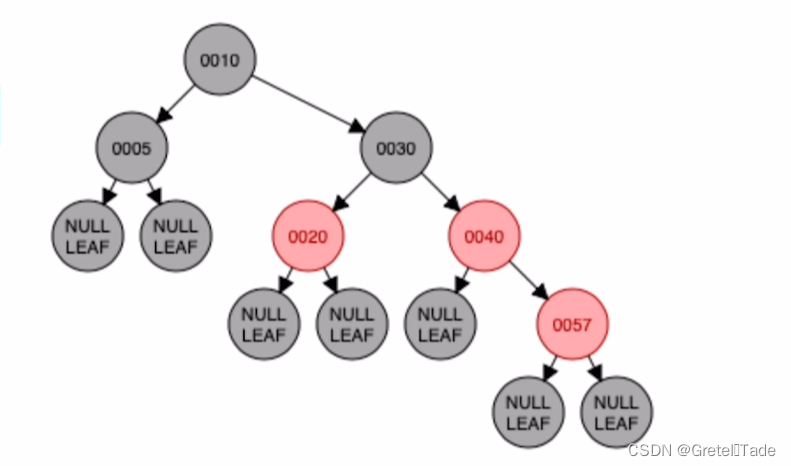
这个也不是红黑树,因为不满足 “不红红” 的特性。
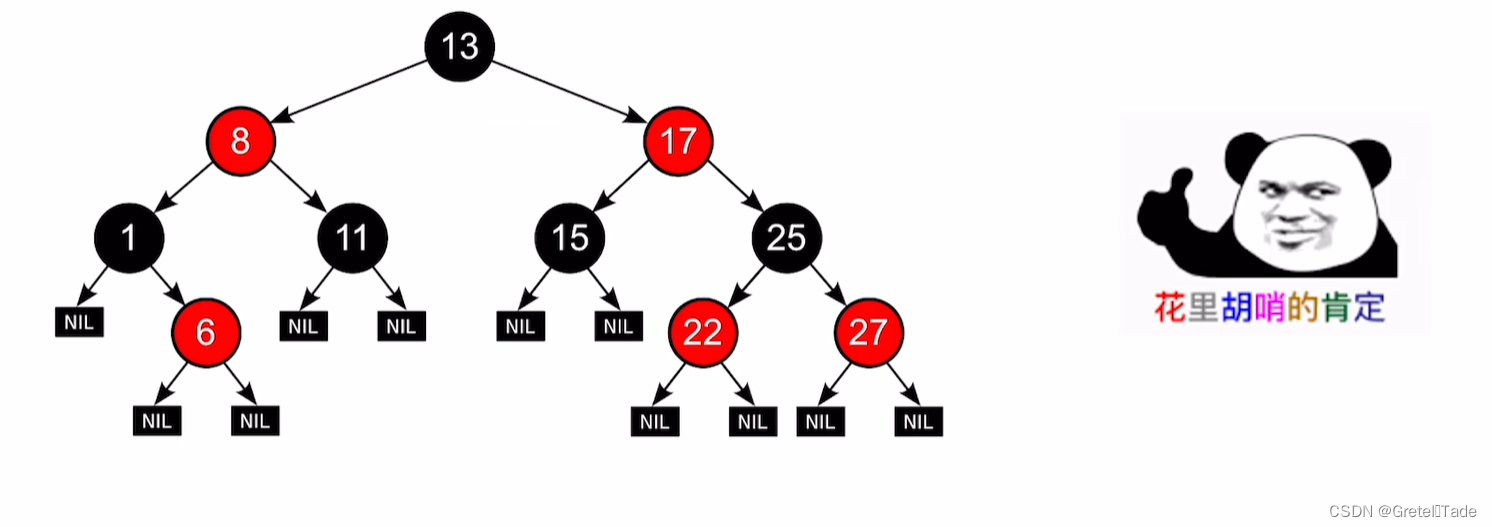
示例3: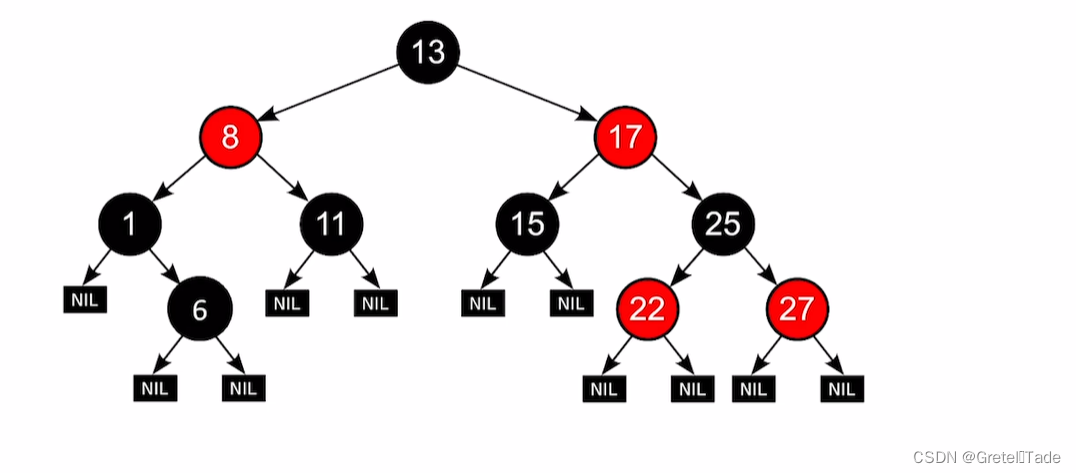
这个也不是红黑树,可能有点不太好看,看到13->8->1->6 这条路径,发现有什么不同呢?很明显,这里不满足 “黑路同” 的性质,相较于其他路径这里多了一个黑色节点的数量。
这一期就先介绍到这里,先初步认识一下红黑树,下一期我们就正式开始进入到了红黑树的深入学习,包括节点的插入和删除等操作,我们下次见咯!
分享一张壁纸:
相关文章:

数据结构-----红黑树简介
目录 前言 1.什么是红黑树? 2.为什么需要红黑树?(与AVL树对比) 3.红黑树的特性 前言 在此之前我们学习过了二叉排序树和平衡二叉树(AVL树),这两种树都是属于搜索树的一种,那么今天…...

哈佛教授因果推断力作:《Causal Inference: What If 》pdf下载
因果推断是一项复杂的科学任务,它依赖于多个来源的三角互证和各种方法论方法的应用,是用于解释分析的强大建模工具,同时也是机器学习领域的热门研究方向之一。 今天我要给大家推荐的这本书,正是因果推断领域必读的入门秘籍&#…...

Drecom 的《Eternal Crypt - Wizardry BC -》加入 The Sandbox 啦!
经典 “Wizardry” 游戏系列的新区块链迭代将通过全球合作拓展 Web3 游戏宇宙。 我们非常高兴地宣布,沙盒游戏公司与富有远见的传奇游戏《Wizardry》系列创造者 Drecom 将建立充满活力的合作伙伴关系。我们将共同推出《Eternal Crypt - Wizardry BC -》,…...

外贸网站流量下降可能是这五点原因造成的
随着互联网的发展,企业开始重视网站优化,越来越多的人开始从事网站优化工作,然而真正做起来,很多站长朋友并非一帆风顺,往往越到很多问题,比如外贸网站流量出现异常下降情况,但很多时候在遇到外…...
交通部 EDI是什么?如何处理?
交通部于1996年开始实施《国际集装箱运输电子信息传输和运作系统及示范工程》,即在中国远洋运输集团、上海口岸、宁波口岸、天津口岸和青岛口岸建立 EDI 示范工程。 交通部 EDI 的数据结构 电子口岸或者其他物流企业需要确保能够生成和解析符合交通部要求的EDI数据…...
【Redis】Java Spring操作redis
目录 引入Redis依赖StringRedisTemplate使用String使用List使用Set使用hash使用zset 引入Redis依赖 StringRedisTemplate 此处RedisTemplate是把这些操作Redis的方法,分成了几个类别,分门别类的来组织的。 此处提供的一些接口风格,和原生的Re…...

如何养好一个微信新号?
最近听到一句话,“微信是个完整的互联网”。 你还真别说,真是。如果你还觉得微信只是个聊天视频打电话的工具,那可就有信息差了。 微信有各种各样的小程序,有打车的,有交话费的,有游戏,可以说&a…...

flutter问题汇总
一直卡在building a flutter app for general distribution; AS Message窗口显示 依赖下载失败: 1、修改仓库地址的配置:android/build.gradle repositories {maven { url https://download.flutter.io }maven { url "https://maven.a…...
2.1 初探大数据
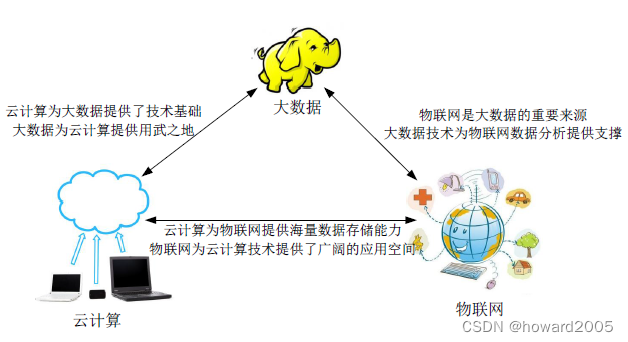
文章目录 零、学习目标一、导入新课二、新课讲解(一)什么是大数据(二)大数据的特征1、Volume - 数据量大2、Variety - 数据多样3、Velocity - 数据增速快4、Value - 数据价值低5、Veracity - 数据真实性 (三࿰…...

论自动化测试中的xpath | 多语言测试最新案例
XPath(XML Path Language)是一门在XML文档中查找信息的语言。XPath是XML处理中非常重要的组成部分,能大大简化文档的解析和处理。它与XSLT、XPointer等标准一起被广泛应用于XML的解析处理。 一般情况下,xpath主要应用在以下几个方…...
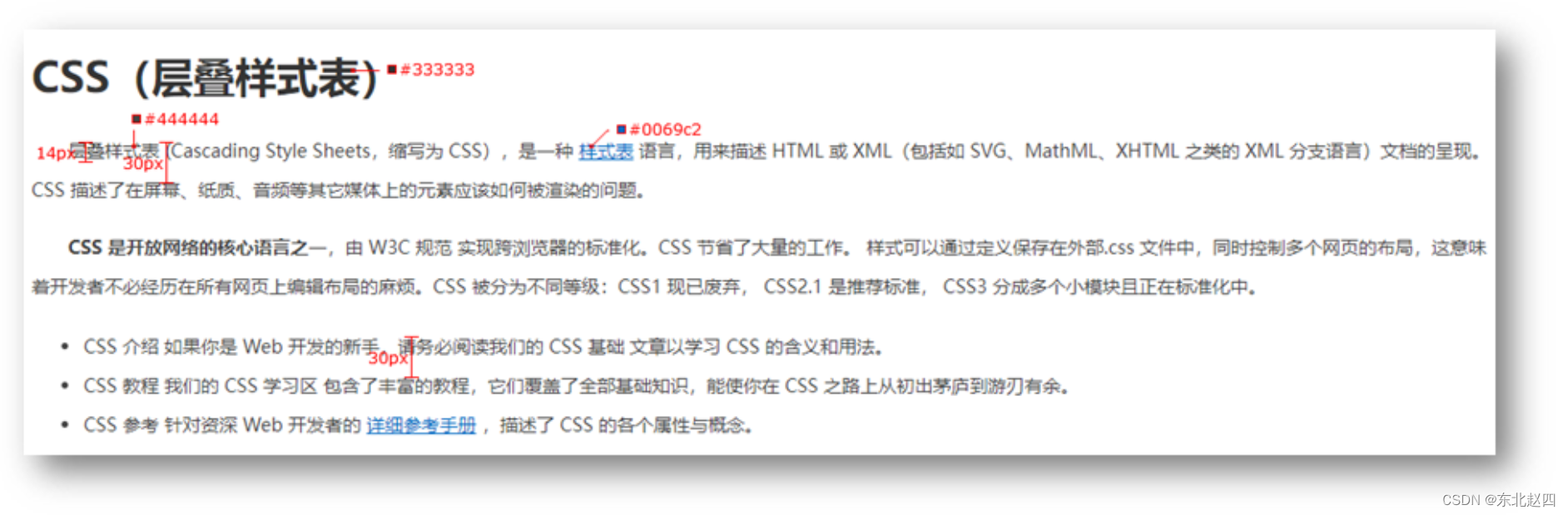
CSS基础详细解析(附带综合小练习)
目标:掌握 CSS 属性基本写法,能够使用文字相关属性美化文章页。 01-CSS初体验 层叠样式表 (Cascading Style Sheets,缩写为 CSS),是一种 样式表 语言,用来描述 HTML 文档的呈现(美化内容&#…...

react中ant.design框架配置动态路由
目录 什么是动态路由? 应用场景: ant.design动态路由如何配置: 首先:找到app.tsx文件 然后:找到menuHeaderRender 其次:修改menuHeaderRender为menuDataRender编辑 最后:在箭头函数里re…...

Linux运行环境搭建系列-Openresty安装
安装Openresty 构建环境:腾讯云CentOS 7.9。 更新云库 yum update添加&&安装云库 wget https://openresty.org/package/centos/openresty.repo sudo mv openresty.repo /etc/yum.repos.d/ sudo yum check-update sudo yum install openresty安装命令行工具…...
React TreeSelect设置默认展开项的方法
需要实现TreeSelect组件的onTreeExpand、treeExpandedKeys方法。 代码样例如下: 1.TreeSelect标签部分 render() {const {codeselect} this.props;const {treeExpandedKeys} this.state ................<TreeSelectshowSearch{false}dropdownStyle{{ maxHei…...
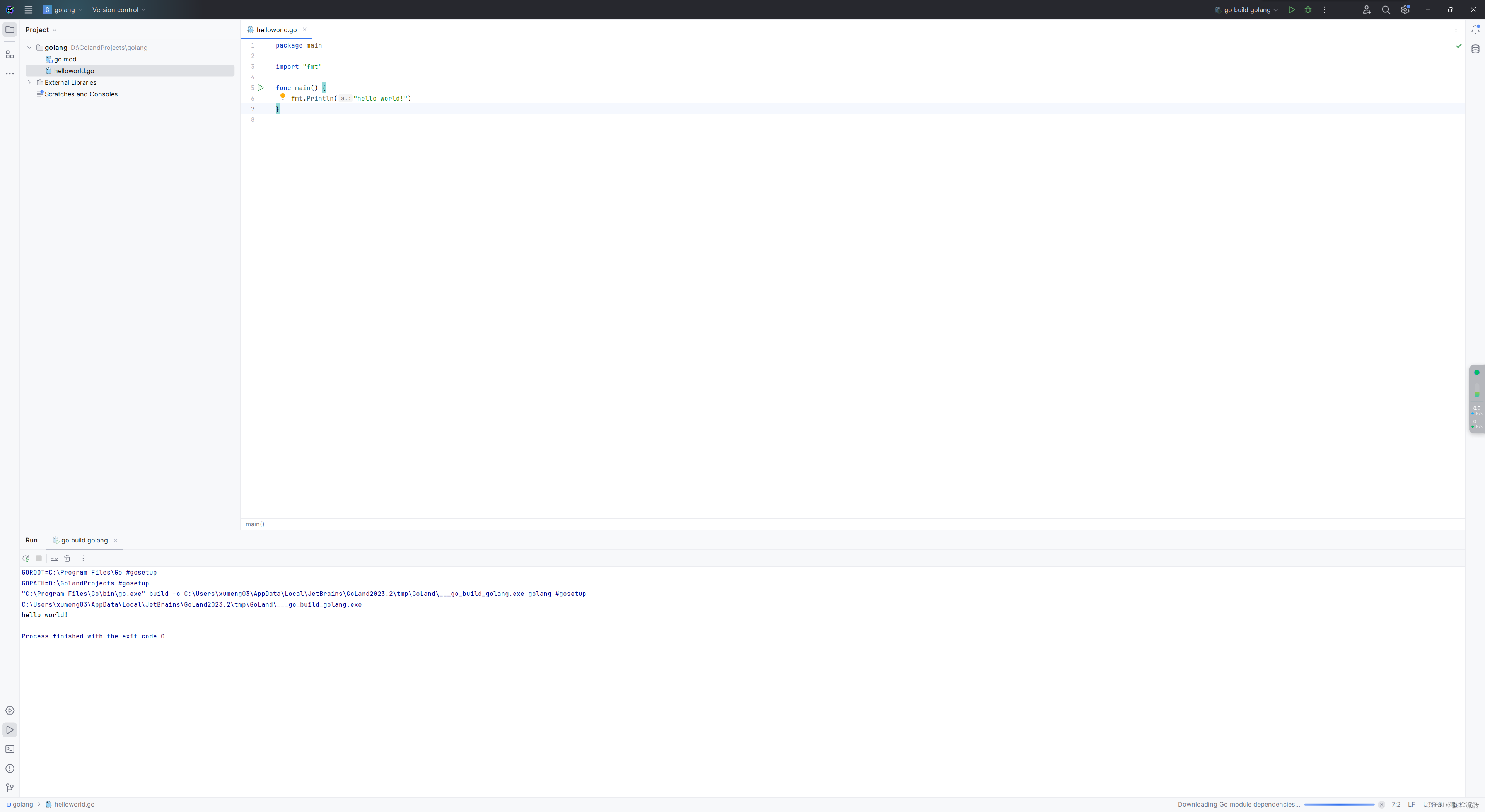
Golang基础学习笔记
Golang基础学习笔记 1、下载安装 1.1、下载 Golang下载地址:https://golang.google.cn/dl/ 1.2、安装 1.3、环境变量 # GOPATH D:\GolandProjects# GOPROXY https://mirrors.aliyun.com/goproxy# 启用Go模块支持 go env -w GO111MODULEon1.5、验证安装/配置 1.…...
ES _bulk 批量操作用法
es 的 bulk 操作,是用来批量发送请求,或者理解为批量操作的。 支持4种操作 bulk 支持多种操作,如下create、index、update、delete。 create 如果文档不存在就创建,但如果文档存在就返回错误index 如果文档不存在就创建&#x…...

LCR 176.判断是否为平衡二叉树
题目来源: leetcode题目,网址:LCR 176. 判断是否为平衡二叉树 - 力扣(LeetCode) 解题思路: 若树中任意节点左子树是平衡二叉树,右子树是平衡二叉树 且该节点左右子树平衡,则该树…...

跨境商城源码有哪些独特的功能和优势
1. 强大的跨境支付功能 跨境商城源码具备强大的跨境支付功能,支持多种支付方式,包括信用卡、支付宝、微信支付等。该功能遵循国际支付标准,能够确保支付过程的安全性和可靠性,为用户提供便捷的跨境购物体验。 2. 多语言和多货币支…...
latex如何对.pdf格式的图片实现裁剪
目录 问题描述: 问题解决: 问题描述: 在使用draw.io进行绘图,导出的时候不知道为什么周围会有留白,比如下图: 在导入latex的时候,会因为两侧的留白导致整张图片缩小。 如果直接进行裁剪.pdf&a…...
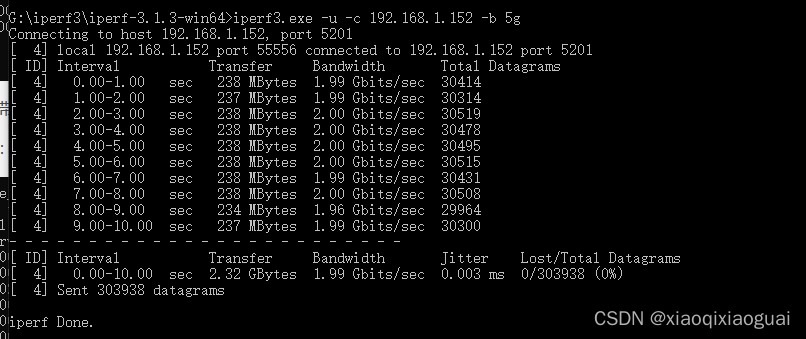
windows10下 iperf3测试带宽
iperf3下载网址:iPerf - Download iPerf3 and original iPerf pre-compiled binaries 可以用来测试TCP以及UDP带宽质量 通俗来说是用来测试网速的 准备:两台设备 1. 根据自己的设备选择下载工具(两台都要有,这里我用的Window…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...
详解:相对定位 绝对定位 固定定位)
css的定位(position)详解:相对定位 绝对定位 固定定位
在 CSS 中,元素的定位通过 position 属性控制,共有 5 种定位模式:static(静态定位)、relative(相对定位)、absolute(绝对定位)、fixed(固定定位)和…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...
