代码随想录Day20 回溯算法 LeetCode77 组合问题
以下内容更详细解释来自于:代码随想录 (programmercarl.com)
1.回溯算法理论基础
回溯法也叫回溯搜索法,是搜索法的一种,我们之前在二叉树中也经常使用到回溯来解决问题,其实有递归就有回溯,有的时候回溯隐藏在递归之下,我们不容易发觉,今天我们来详细介绍一下什么是回溯,它能解决哪些问题.
回溯法效率
回溯法的效率是不高的,回溯的本质是穷举,因为有些问题能用回溯法解决出来就不错了,别无他法,只能使用这个暴力方法
回溯法,一般可以解决如下几种问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
提供一个八皇后小游戏hhh:【死亡8皇后】小游戏_游戏规则玩法,高分攻略-2345小游戏
理解回溯法的方式
不要光靠脑子想,要将这种回溯具象化,想象成树形结构,任何回溯法解决的问题都可以转化为树形结构来解决问题.
因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度.
递归就要有终止条件,所以必然是一棵高度有限的树(N叉树).
回溯法代码模板(伪代码)
首先是函数参数和返回值
一般无需返回值,参数很多,一般边写边定,函数名一般定为backtracking
void backtracking(参数)终止条件
我们说可以将回溯算法想像成一个树形结构,那么我们就一定有终止条件,一般到达终止条件(叶子结点),也就是我们收获答案的时候,相关为伪代码如下
if (终止条件) {存放结果;return; }回溯搜索的遍历过程
上文中我们说回溯的树的宽度取决于元素个数,回溯深度取决于递归深度,如图所示
回溯算法遍历的伪代码如下
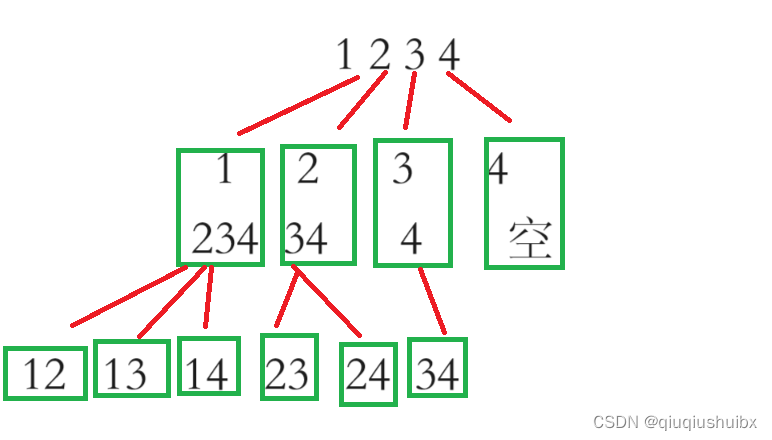
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果 }注意这里的撤销,假设我们要求1234中size为2的组合,有 12 13....这里假设我们第一个节点是12,这里我们要得到13就得将2pop出去,也就是我们回溯撤销的过程.
回溯模板(全)
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果} }
2.经典例题 :LeetCode T77 组合问题


题目链接:77. 组合 - 力扣(LeetCode)
题目思路:
我们说递归有三部曲,这里我们回溯也有三部曲,这里我们首先定义一个path变量,来存放我们每条路径上的结果,因为这里我们可以将回溯过程想象成n叉树,所以叶子结点的结果也可以想象成路径的结果,然后定义一个result数组来存放所有路径的集合,这里我们定义为全局变量,下面函数实现中直接操作即可.
List<Integer> path = new ArrayList<>(); List<List<Integer>> result = new ArrayList<>();
我们以1234中排列2个数字,即n = 4,k = 2为例,画出如下图
回溯三部曲
1.确定函数参数和返回值
这里n和k肯定是需要的,还有我们需要一个参数就是从哪里开始,于是我们定义一个变量startIndex来记录每次递归开始的逻辑,比如第一次从1开始,第二次从2开始
public void backtracking(int n, int k,int startIndex)2.确定终止条件
这里的终止条也是收割结果的时候,我们发现树的叶子节点就是我们所要的结果,我们写出如下代码
//终止条件if(path.size() == k){result.add(new ArrayList<>(path));return;}3.确定一次递归(回溯)过程
这里我们按照上文所说就是我们for循环该登场了,这个时候我们的循环就得从startIndex开始到n结束,里面需要做的事情就是path.add元素,再进行backtracking,最后得pop元素进行一次回溯的过程,这里我们可以想象假设上面这个1234的例子,这里我收集了12这个例子,我想收获13这个结果是不是得将2弹出再将3进行添加呀,下面是代码演示
//for循环for(int i = startIndex;i<=n;i++){path.add(i);backtracking(n,k,i+1);path.remove(path.size()-1);}
题目代码:
class Solution {List<Integer> path = new ArrayList<>();List<List<Integer>> result = new ArrayList<>();public List<List<Integer>> combine(int n, int k) {backtracking(n,k,1);return result;}public void backtracking(int n, int k,int startIndex){//终止条件if(path.size() == k){result.add(new ArrayList<>(path));return;}//for循环for(int i = startIndex;i<=n;i++){path.add(i);backtracking(n,k,i+1);path.remove(path.size()-1);}}
}代码优化
还是以上面1234举例,这里我们可以进行一次剪枝,假设我们n = 4,k = 4我们就会发现startIndex取2后面的值就毫无意义了,这里我们就可以对这种情况剪枝,如果后面的元素不足以我构成我们的一次正确的结果,就不要去遍历它了
优化过程如下:
已经选择的元素个数:path.size();
还需要的元素个数为: k - path.size();
在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2,这里都是合理的
只需修改一下for循环的区间即可
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++)
相关文章:
代码随想录Day20 回溯算法 LeetCode77 组合问题
以下内容更详细解释来自于:代码随想录 (programmercarl.com) 1.回溯算法理论基础 回溯法也叫回溯搜索法,是搜索法的一种,我们之前在二叉树中也经常使用到回溯来解决问题,其实有递归就有回溯,有的时候回溯隐藏在递归之下,我们不容易发觉,今天我们来详细介绍一下什么是回溯,它能…...
免费获取天气预报的API接口(Json格式)
免费获取天气预报的API接口(Json格式) 1、接口地址2、城市代码 1、接口地址 当需要获取某个城市天气数据json时候,需要传入一个城市代码编码作为入参,地址: http://t.weather.itboy.net/api/weather/city/xxxxx &…...

安卓程序执行入口
Android程序执行入口 Android应用程序的执行入口是在一个特定的 Java 类中,通常是 MainActivity 或 SplashActivity,具体取决于应用的设计和结构。 Android应用程序的执行入口通常通过以下方式进行定义: 在 AndroidManifest.xml 文件中&am…...
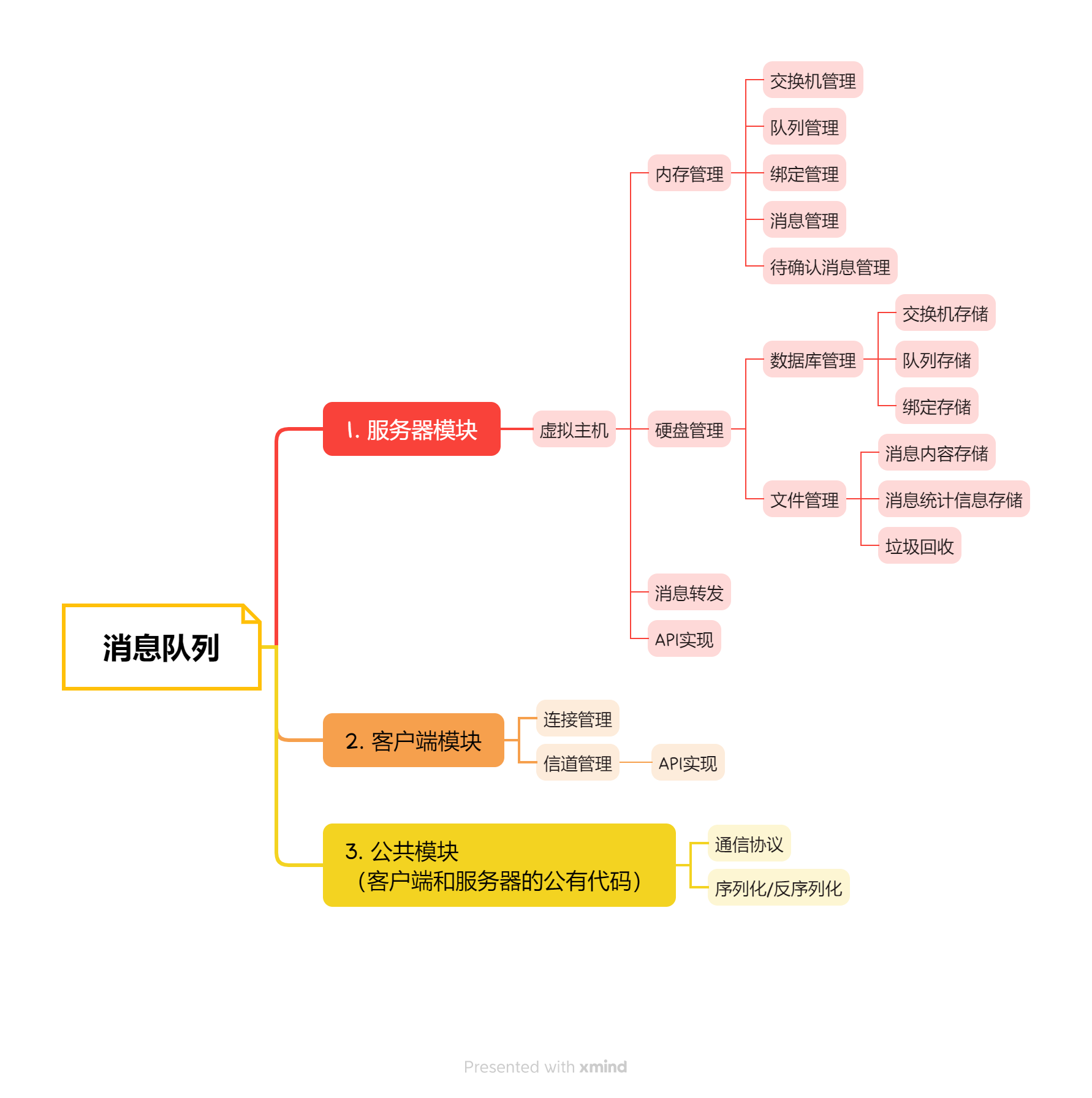
消息队列(中间件)
通信协议: 为了实现客户端和服务器之间的通信来完成的逻辑,基于TCP实现的自定义应用层协议。通过这个协议,完成客户端–服务器远程方法调用。 序列化/反序列化: 通过网络传输对象把对象存储到硬盘上。 序列化:把对象转化为二进制的…...

Java|学习|异常
1.异常 1.1 异常 1.1.1 概述 异常:就是程序出现了不正常的情况。 Error:严重问题,不需要处理。 Exception:称为异常类,它表示程序本身可以处理的问题。 RuntimeException:在编译器不检查,出…...

nextjs项目修改启动端口号,以及开发启动后自动打开浏览器
next版本:13.5.4 一、修改端口 在package.json文件当中修改启动命令 "scripts": {"dev": "next dev -p 3100","build": "next build","start": "next start","lint": "ne…...
微服务架构 | 超时管理
INDEX LSA 级别与全年停机时间速查表LSA 级别实战TP 性能超时时间设计原则 LSA 级别与全年停机时间速查表 计算公式:60 * 60 * 24 * 365 * (1-LSA) 31,536,000 * (1-LSA) 系统级别LSA级别全年停机时间099.999%5分钟099.99%52分钟199.9%8.8小时299%3.65 天 LSA…...

Qt 样式表大全整理
【QT】史上最全最详细的QSS样式表用法及用例说明_qt样式表使用大全_半醒半醉日复日,花落花开年复年的博客-CSDN博客 QT样式表的使用_qt 设置按下 release hover 按钮样式表_create_right的博客-CSDN博客 QPushButton {border-image: url(:/Start_Stop.png); } QPu…...

k8s-10 cni 网络
k8s通过CNI接口接入其他网络插件来实现网络通讯。目前比较流行的插件有flannel,calico等。 CNI插件存放位置: # cat /etc/cni/net.d/10-flannel.conflist 插件使用的解决方案如下: 虚拟网桥,虚拟网卡,多个容器共用一个虚拟网卡进行通信。多路复用: Mac…...

IDEA中.gitignore配置不生效的解决方案
一、创建项目 二、执行以下Git命令 git rm -r --cached . git add . git commit -m "update .gitignore"...

SparkContext 与 SparkContext 之间的区别是什么
SparkContext 是 Spark 的入口点,它是所有 Spark 应用程序的主要接口,用于创建 RDD、累加器、广播变量等,并管理与 Spark 集群的连接。在一个 Spark 应用程序中只能有一个 SparkContext。 而 SparkSession 是 Spark 2.0 新增的 API࿰…...

lv8 嵌入式开发-网络编程开发 17 套接字属性设置
1 基本概念 设置套接字的选项对套接字进行控制除了设置选项外,还可以获取选项选项的概念相当于属性,所以套接字选项也可说是套接字属性有些选项(属性)只可获取,不可设置;有些选项既可设置也可获取 2 选项…...

VulnHub Alice
一、信息收集 发现开发了22、80 2.访问ip,右击查看源代码 发现需要利用X-Forwarded-For 火狐插件:X-Forwarded-For Header 挂上代理后: 出现以下页面: 先注册一个账户,然后再登录 发现有参数进行传参 发现传参&a…...

AUTOSAR组织发布20周年纪念册,东软睿驰NeuSAR列入成功案例
近日,AUTOSAR组织在成立20周年之际发布20周年官方纪念册(20th Anniversary Brochure),记录了AUTOSAR组织从成立到今天的故事、汽车行业当前和未来的发展以及AUTOSAR 伙伴关系和合作在重塑汽车方面的作用。东软睿驰提报的基于AUTOS…...

转行网络安全是否可行?
一、前言 其实很多的IT大佬之前也不是专门学计算机的,都是后期转行的。而且大学学什么专业,对后期的工作真的没有太大关系,这也是现在高校的教育现状。有80%的学生都是通过临时抱佛脚,考前冲刺拿到毕业证书的。下面就带大家详细分…...
netca_crypto.dll找不到怎么修复?详细解决办法和注意事项
当你在使用计算机时,突然出现了一个错误提示:“netca_crypto.dll 找不到”。不知道该如何解决这个问题?其实要解决是非常的简单的,今天我们将为你提供几种修复 netca_crypto.dll 找不到的解决方法和一些注意事项。在深入探讨修复方…...

axios的请求中断和请求重试
请求中断 场景:1、假如一个页面接口太多、或者当前网络太卡顿、这个时候跳往其他路由,当前页面可以做的就是把请求中断掉(优化)2、假如当前接口调取了第一页数据,又调去了第二页的数据,当我们调取第二页数…...
视频怎么压缩?视频太大这样处理变小
在当今时代,视频已经成为了我们日常生活中不可或缺的一部分,然而,视频文件往往非常大,给我们的存储和传输带来了很大的不便,那么,如何有效地压缩视频呢? 一、使用压缩软件 首先我们给大家分享一…...
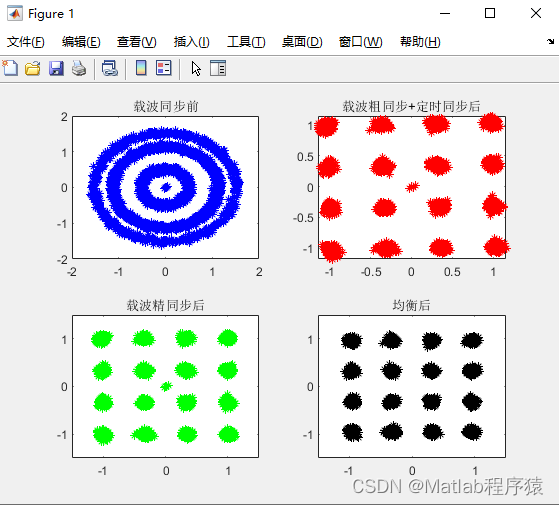
【MATLAB源码-第48期】基于matlab的16QAM信号盲解调仿真。
操作环境: MATLAB 2022a 1、算法描述 16QAM (16个象限幅度调制) 是一种广泛使用的数字调制技术。在无线和有线通信系统中,为了在固定的带宽内发送更多的信息,高阶调制如16QAM被使用。下面是16QAM盲解调的基本步骤、优缺点及应用场景。 16Q…...

自我介绍思考
1.引导面试官有重点的看你简历 2.在引导部分暗示他我是最适合这个岗位的 面试官在考察什么? a.你的表述是否一致b.考察你的语言表达能力,逻辑思维能力,总结概括能力c.考察你对现场的把控能力d.对时间的把控能力 怎么做? 1.写逐…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

