C++算法前缀和的应用:分割数组的最大值的原理、源码及测试用例
分割数组的最大值
相关知识点
C++算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例:付视频课程
二分 过些天整理基础知识
题目
给定一个非负整数数组 nums 和一个整数 m ,你需要将这个数组分成 m 个非空的连续子数组。
设计一个算法使得这 m 个子数组各自和的最大值最小。
示例 1:
输入:nums = [7,2,5,10,8], m = 2
输出:18
解释:
一共有四种方法将 nums 分割为 2 个子数组。
其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18,在所有情况中最小。
示例 2:
输入:nums = [1,2,3,4,5], m = 2
输出:9
示例 3:
输入:nums = [1,4,4], m = 3
输出:4
提示:
1 <= nums.length <= 1000
0 <= nums[i] <= 10^6
1 <= m <= min(50, nums.length)
解法一:暴力解法
时间复杂度O(nnm),n是nums的长度。vMaxSum共有m*n种状态,求每种状态需的时间复杂度是O(n)。vPreSum记录前缀和,vMaxSum[i][j] 记录将nums[0,j]分成i个子数组的最大和。j’取值范围[0,j),vMaxSum[i][j]就是所有max(vMaxSum[i-1][j’],vPreSum[j+1] - vPreSum[j’])的最小值。这个时间复杂度在通过和不通过的边缘。
解法二:滑动窗口
假定j的j1是x,则当j增加时,x不变或增加。 当j++,vMaxSum[i-1][j’]不变,vPreSum[j+1] - vPreSum[j’] 增加。下面用因果表来证明。令L(j,x)= vMaxSum[i-1][x] R(j,x) = vPreSum[j+1] - vPreSum[x] |。
如果L(j,x)<= R(j,x)。x减少后,左式减少或不变,右式增加或不变。i++后,右式变大或不变。所以x减少只会让右式变大或不变。而右式显然大于左式,所以减少左式不会减少最大值。
| 规章编号 | 因 | 证明 | 果 |
|---|---|---|---|
| 假设一 | 合适的j1就是x | ||
| 假设二 | L(j,x)> R(j,x) | ||
| 推论一 | 假设一 假设二 | x–后,L变小,R变大。如果L(j,x-1) >= R(j,x-1),结合假设二,x-1比x更合适。与假设一矛盾。 | L(j,x-1) < R(j,x-1)] |
| 推论二 | 对于j+1,取x最大和为L(j,x)或R(j+1,x);取x-1,最大和为R(j+1,x-1) | ||
代码
class Solution {
public:
int splitArray(vector& nums, int k) {
m_c = nums.size();
vector vPreSum(1);
for (const auto& n : nums)
{
vPreSum.emplace_back(n + vPreSum.back());
}
vector pre(m_c);
for (int i = 0; i < m_c; i++)
{
pre[i] = vPreSum[i + 1] - vPreSum[0];
}
for(int i = 1 ; i < k ; i++ )
{
vector dp(m_c,-1);
int k = i ;
for (int j = i; j < m_c; j++)
{
k–;
int iMax = INT_MAX;
#define MaxCro (max(pre[k], vPreSum[j + 1] - vPreSum[k+1]))
while ((k < j) && (MaxCro <= iMax))
{
iMax = MaxCro;
k++;
}
dp[j] = iMax;
}
pre.swap(dp);
}
return pre.back();
}
int m_c;
};
测试用例
template
void Assert(const vector& v1, const vector& v2)
{
if (v1.size() != v2.size())
{
assert(false);
return;
}
for (int i = 0; i < v1.size(); i++)
{
assert(v1[i] == v2[i]);
}
}
template
void Assert(const T& t1, const T& t2)
{
assert(t1 == t2);
}
int main()
{
vector nums = { 1,2,3,4,5,6 };
int k = 2;
auto res = Solution().splitArray(nums, k);
Assert(res, 11);
nums = { 1, 0, 3, 3, 0, 6 };k = 2;res = Solution().splitArray(nums, k);
Assert(res, 7);nums = { 6,5,3,2,2,1 };
k = 5;
res = Solution().splitArray(nums, k);
Assert(res, 6);nums = { 1,0,3,3,0,1 };
k = 5;
res = Solution().splitArray(nums, k);
Assert(res, 3);//CConsole::Out(res);
}
2023年一月版:二分
class Solution {
public:
int splitArray(vector& nums, int k) {
int iMax = *std::max_element(nums.begin(), nums.end());
int iSum = std::accumulate(nums.begin(), nums.end(),0);
int left = iMax-1, right = iSum;while (left+1 < right){int iMid = (left + right) / 2;if (NeedK(nums, iMid) <= k){right = iMid;}else{left = iMid;}}return right;}int NeedK(const vector<int>& nums, int iMaxSum){int iNeedK = 1;int iSum = 0;for (const auto& n : nums){if (iSum + n > iMaxSum){iSum = n;iNeedK++;}else{iSum+=n;}}return iNeedK;}
};
2023年8月版也是二分
class Solution {
public:
int splitArray(vector& nums, int k) {
int iSum = std::accumulate(nums.begin(), nums.end(), 0);
int left = -1, r = iSum;
while (r > left + 1)
{
const auto mid = left + (r - left) / 2;
if (Is(nums, mid, k))
{
r = mid;
}
else
{
left = mid;
}
}
return r;
}
bool Is(const vector& nums, const int iMaxSum, int k)
{
k–;//可以分配的新组
int iHas = 0;
for (const auto& n : nums)
{
iHas += n;
if (iHas > iMaxSum)
{
k–;
iHas = n;
if (n > iMaxSum)
{
return false;
}
}
}
return k >= 0;
}
};
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《闻缺陷则喜算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 鄙人想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 墨家名称的来源:有所得以墨记之。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17

相关文章:

C++算法前缀和的应用:分割数组的最大值的原理、源码及测试用例
分割数组的最大值 相关知识点 C算法:前缀和、前缀乘积、前缀异或的原理、源码及测试用例:付视频课程 二分 过些天整理基础知识 题目 给定一个非负整数数组 nums 和一个整数 m ,你需要将这个数组分成 m 个非空的连续子数组。 设计一个算法…...
gitlab自编译 源码下载
网上都是怎么用 gitlab,但是实际开发中有需要针对 gitlab 进行二次编译自定义实现功能的想法。 搜索了网上的资料以及在官网的查找,查到了如下 gitlab 使用 ruby 开发。 gitlab 下载包 gitlab/gitlab-ce - Packages packages.gitlab.com gitlab/gitl…...
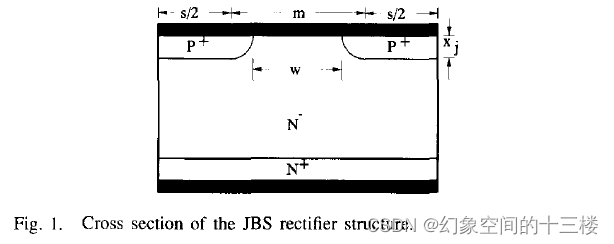
SBD(Schottky Barrier Diode)与JBS(Junction Barrier Schottky)
SBD和JBS二极管都是功率二极管,具有单向导电性,在电路中主要用于整流、箝位、续流等应用。两者的主要区别在于结构和性能。 结构 SBD是肖特基二极管的简称,其结构由一个金属和一个半导体形成的金属-半导体结构成。 JBS是结势垒肖特基二极…...
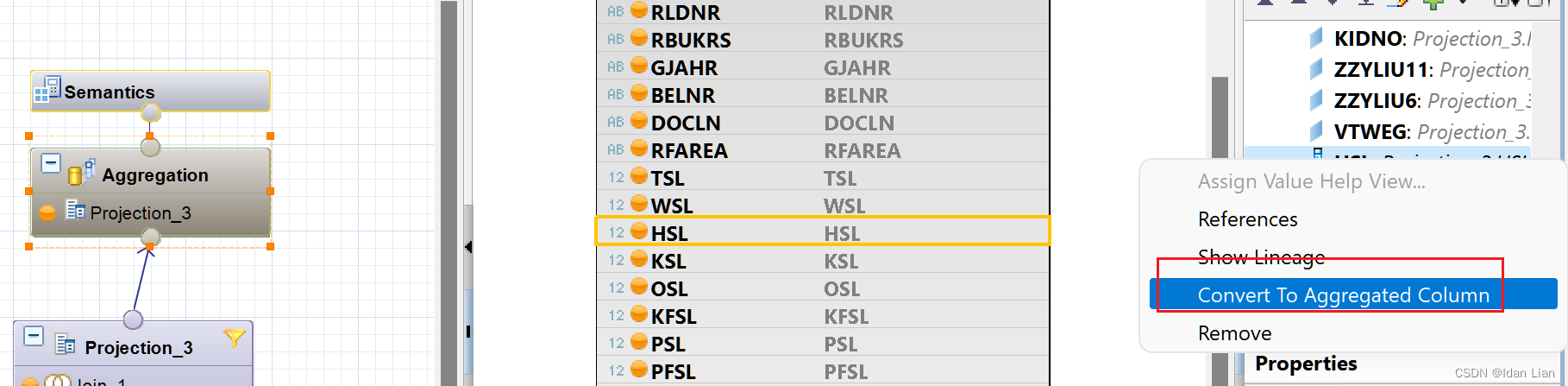
HANA:计算视图-图形化Aggregation组件-踩坑小记(注意事项)
今天遇到在做HANA视图开发的时候,遇到一个事,一直以为是个BUG,可把我气坏了,具体逻辑是这样的,是勇图形化处理的,ACDOCA innerjoin 一个时间维度表,就这么简单,完全按照ACDOCA的主键…...
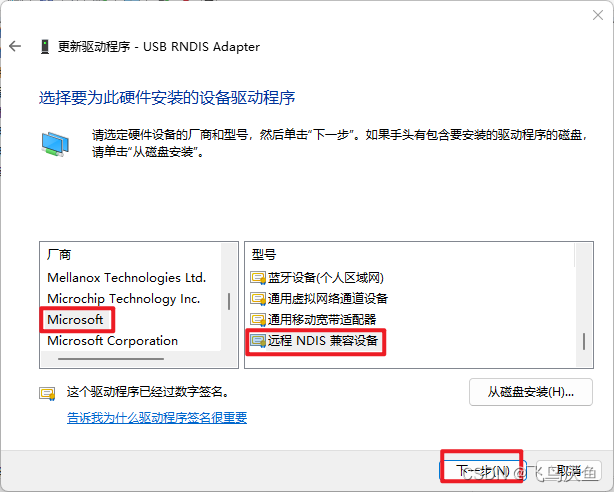
【milkv】更新rndis驱动
问题 由于windows升级到了11,导致rndis驱动无法识别到。 解决 打开设备管理器,查看网络适配器,没有更新会显示黄色的图标。 右击选择更新驱动...

基于混沌博弈优化的BP神经网络(分类应用) - 附代码
基于混沌博弈优化的BP神经网络(分类应用) - 附代码 文章目录 基于混沌博弈优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.混沌博弈优化BP神经网络3.1 BP神经网络参数设置3.2 混沌博弈算法应用 4.测试结果…...
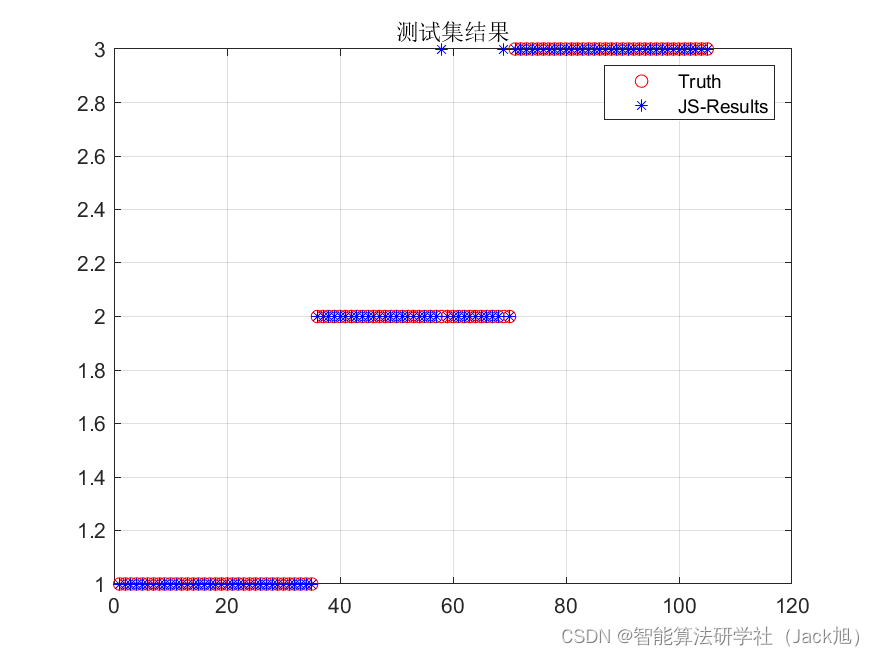
基于人工水母优化的BP神经网络(分类应用) - 附代码
基于人工水母优化的BP神经网络(分类应用) - 附代码 文章目录 基于人工水母优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.人工水母优化BP神经网络3.1 BP神经网络参数设置3.2 人工水母算法应用 4.测试结果…...

【C++】哈希学习
哈希学习 unordered系列关联式容器哈希结构除留余数法哈希冲突闭散列线性探测二次探测 负载因子开散列开散列增容 闭散列 VS 开散列字符串哈希算法 线性探测 & 二次探测实现拉链法实现 unordered系列关联式容器 unordered系列关联式容器是从C11开始,STL提供的。…...
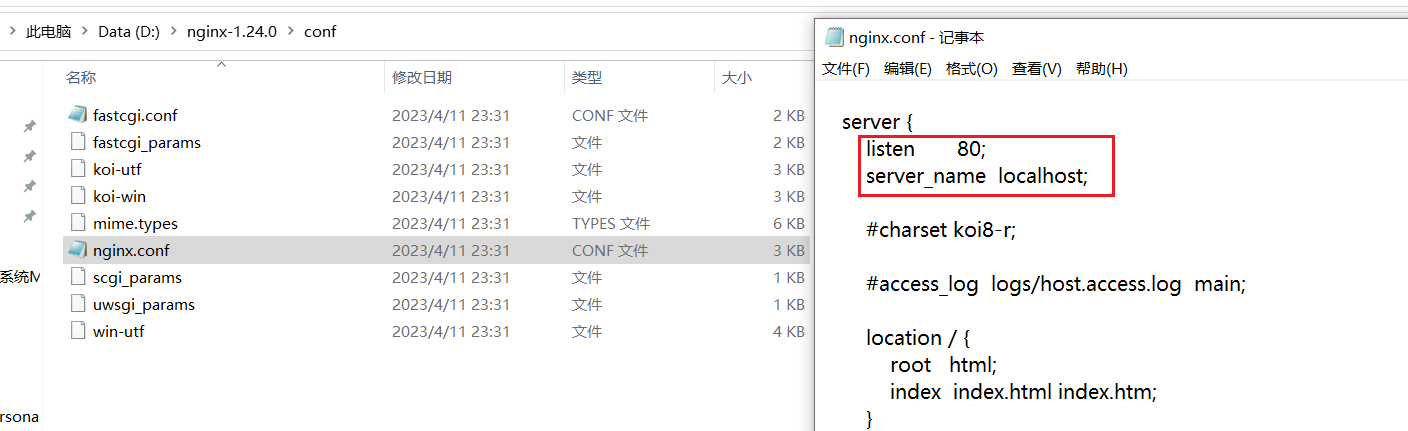
Nginx的安装——window环境
1、下载Nginx 在官网下载稳定版本: http://nginx.org/en/download.html 以nginx/Windows-1.24.0为例,直接下载 nginx-1.24.0.zip。 下载后解压,解压后如下: 2、启动nginx 在window环境下启动nginx的方法有以下两种: …...
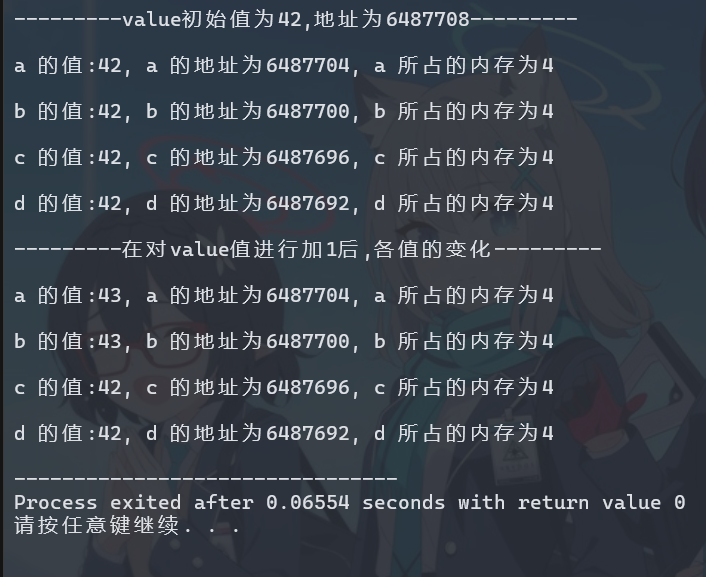
C语言笔记之指针
一.指针含义 1.a、*a与&a的区别 a存储指向变量的地址,*a为指针的值,&a为指针的地址 #include <stdio.h>int main(){/** 测试代码部分一 **/int a12;int *b1;b1&a1;printf(" a1 %d, &a1 %d, b1 %d, *b1 %d, &b1 %d\n\n",a1,&a1…...
(二)】)
【 OpenGauss源码学习 —— 列存储(CU)(二)】
列存储(CU)(二) 概述GetCUHeaderSize 函数Compress 函数CU::FillCompressBufHeader 函数CU::CompressNullBitmapIfNeed 函数CU::CompressData 函数 声明:本文的部分内容参考了他人的文章。在编写过程中,我们…...
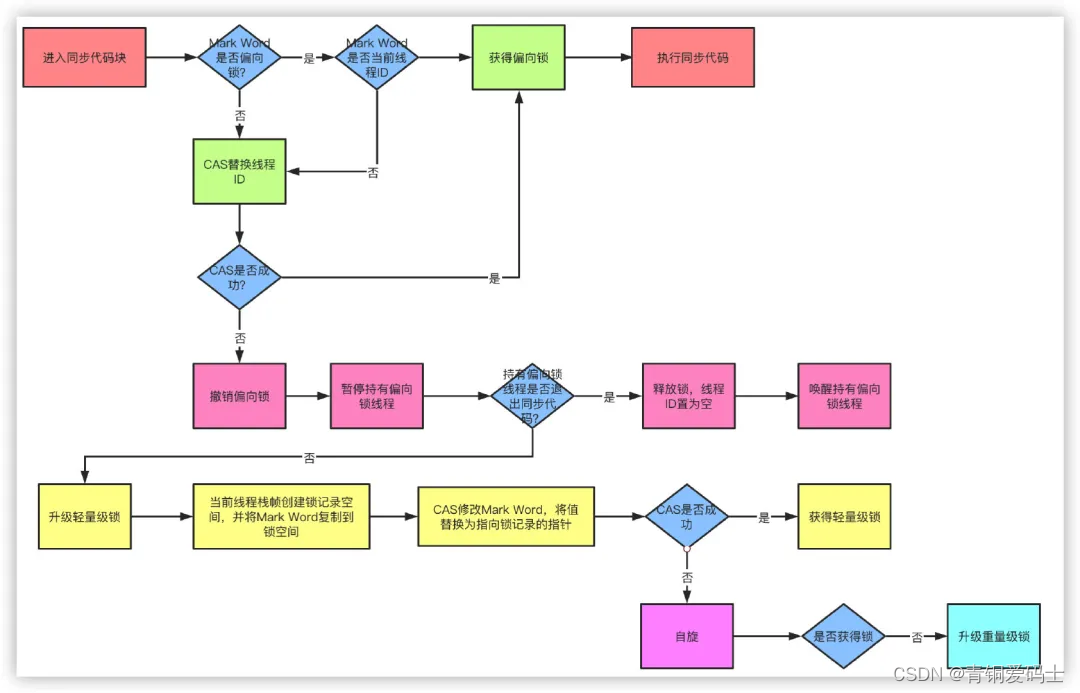
Java并发面试题:(四)synchronized和lock区别
synchronized 关键字 synchronized关键字解决的是多个线程之间访问资源的同步性,synchronized关键字可以保证被它 修饰的方法或者代码块在任意时刻只能有一个线程执行。 另外,在 Java 早期版本中, synchronized属于重量级锁,效率…...

使用Nginx实现采集端和数据分析平台的数据加密传输
1. 需求描述 目前鸿鹄暴露出来的重要ports如下表: 在实际的生产环境中,结合我司的使用场景,需要在鸿鹄前端安装proxy,用以解决如下两个问题: 1.1 实现http到https的强制跳转 企业环境中,一般会关闭http 80端…...

appium---如何判断原生页面和H5页面
目前app中存在越来越多的H5页面了,对于一些做app自动化的测试来说,要求也越来越高,自动化不仅仅要支持原生页面,也要可以H5中进行操作自动化, webview是什么 webview是属于android中的一个控件,也相当于一…...

【WIFI】【WPS】如何从log角度判断WPS 已经连接上
在Android项目中,由于WPS在Framework 接口中已经remove了 只能通过wpa-supplicant 代码中去判断是否连接上了 这段代码log 表示 PBC模式下没有激活 09-21 22:42:16.221503 3782 3782 D wpa_supplicant: wlan0: 0: 04:cf:4b:21:a0:3e ssid=Openwrt-WPS-tp wpa_ie_len=0 rsn…...

[正式学习java①]——java项目结构,定义类和创建对象,一个标准javabean的书写
目录 一、创建第一个java文件 二、 初始类和对象 三、符合javabean规范的类 一、创建第一个java文件 要想写代码,你得有文件啊 以前的创建方式: 右键新建文本文档,开始写代码,写完改后缀名,保存……这样文件一旦多了…...

day36
今日内容概要 进程基础(操作系统中的概念) 进程调度算法(四种算法) 进程的并行和并发的概念 同步异步阻塞非阻塞的概念 创建进程(进程类Process) Process类的参数 Process类的方法 如何开启多进程 基于TCP协议的高并发程序 进程基础 进程它是操作系统中最重要的概念…...

五. 激光雷达建图和定位方案-开源SLAM
前面内容: 一. 器件选型心得(系统设计)--1_goldqiu的博客-CSDN博客 一. 器件选型心得(系统设计)--2_goldqiu的博客-CSDN博客 二. 多传感器时间同步方案(时序闭环)--1 三. 多传感器标定方案&a…...
SAP MM学习笔记37 - 请求书照合中的 追加请求/追加Credit 等概念/ 请求书的取消
有关请求书照合,之前学习了一部分,现在再来学其中的一些概念。 其实这些概念也许并不常用,但是你又不能不知道,因为客户会问。 有关请求书,贴一些以前学习的文章,以方便阅读。 SAP MM学习笔记33 - 请求书…...

【C#】Winform实现轮播图
复制后,需要修改的代码: 1、图片文件夹路劲:string folderPath "C:\\Users\\Administrator\\Desktop\\images"; 2、项目命名空间:namespace BuildAction 全窗口代码: using System; using System.Colle…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
