pointnet和pointnet++点云分割和分类
目录
1. pointnet
1.1 点云数据的特点
1.2 模型功能
1.3 网络结构
1.3.1 分类网络
1.3.2 分割网络
2. pointnet++
2.1 模型
2.2 sampling layer组件
2.3 grouping layer
2.4 pointnet
1. pointnet
1.1 点云数据的特点
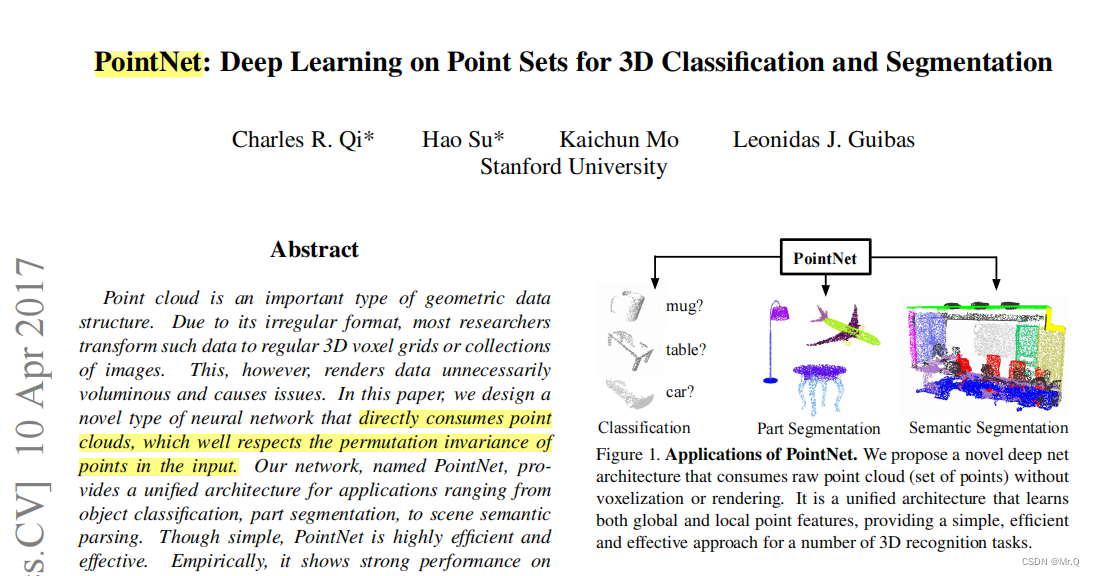
(1)无序性:不同于图像中的像素数组或体积网格中的体素数组,点云是一组没有特定顺序的点。换句话说(permutations of the input set in data feeding order. ),点云中的点集合排列顺序改变了,点云本身的目标类别和分割结果是不变的(符合交换律,比如加法、乘法、取最值等操作)。
(2)点之间的交互:点不是孤立的,而相邻的点形成了一个有意义的子集。因此,该模型需要能够从附近的点捕获局部结构,以及局部结构之间的组合相互作用。
(3)变换无关性:作为一个几何对象,点集的特征表示应该对某些变换是不变的。例如,旋转和平移点不应该修改全局点云类别或点的分割。
1.2 模型功能
(1)模型输入:网络的输入是坐标点集合(x,y,z);
(2)分类输出:输出有两个分支,分类分支输出是k个scores对应k个类别,哪个值大就是那个类别;
(3)分割输出:分割分支输出的是nxm的矩阵scores,有n个点,每个点有m个分数,m个分数对应m个语义分割类别,哪个值大,当前点就属于哪个类别。
1.3 网络结构
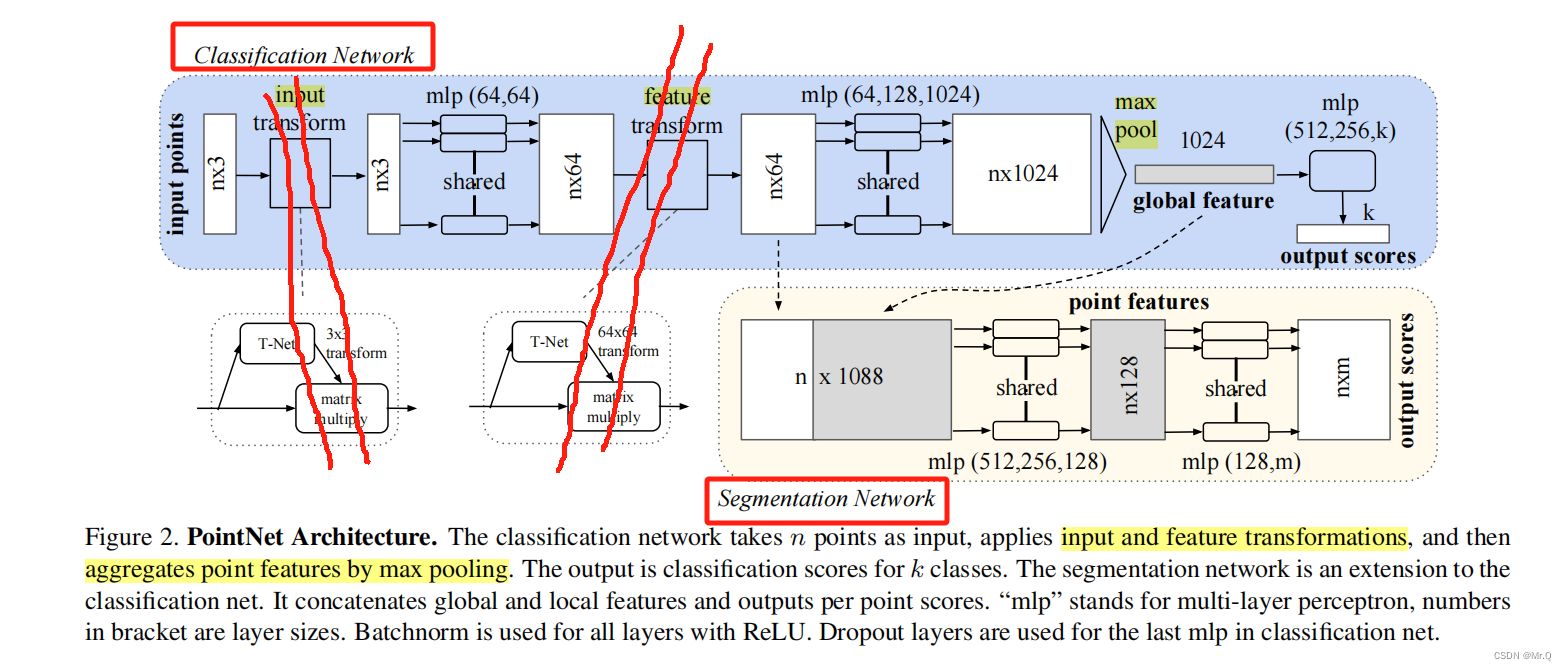
1.3.1 分类网络
(1)input transform和feature transform是个小网络,其中input transform用来预测放射变换矩阵,用于对齐输入的点云数据,feature transform是用来对齐特征数据,后期的论文证明是没多大用处的,可以忽略;
(2)论文中n是1024(均匀采样),论文中只用到了(x,y,z)坐标,所以输入是nx3点云矩阵,首先经过mlp(64,64),即两个多层感知机全连接网络,维度变化3->64->64,输出nx64特征向量;
(3)再经过3个多层感知机,维度变化64->64->128->1024,升维度,输出nx1024特征向量,方便后面的maxpooling提取全局特征(即降维操作);
(4)提取特征后,使用maxpooling操作,提取全局特征,nx1024,每个点有1024维度特征,求所有点的全局特征,就是在每个维度上取最大值,则nx1024 -> 1x1024;这1024个数据就代表真个点云数据的全局特征;
(5)再接一个mlp(512,256,k),作为分类层,1024->512->256->k全连接节点变换,k个类别分数,哪个值大就是那个类别。
1.3.2 分割网络
(1)前面的特征提取层是一样的,提取得到局部特征nx64,和全局特征1x1024;
(2)融合局部特征和全局特征,直接concat在一起,变成nx1084,每个点都有1084维度特征;
(3)再接mlp层,维度变换1084->512->256->128,再接mlp层,维度变化128->128->m,这样特征矩阵变化nx1084 -> nxm;
(4)nxm,即n个点,每个点都有m个类别分数,哪个大,则当前点的分割类别就属于对应的类别。
2. pointnet++
pointnet模型简单一句话,就是mlp提取特征,再经过分类层进行分类,即可完成对输入点云数据的分类,公式概括如下。

其中MAX是最大池化层。
由于只是使用maxpooling来聚合整个点云的特征,pointnet是不能捕获不同尺度下的局部特征。pointnet适用于目标数据的尺度变化不大的场景。
2.1 模型
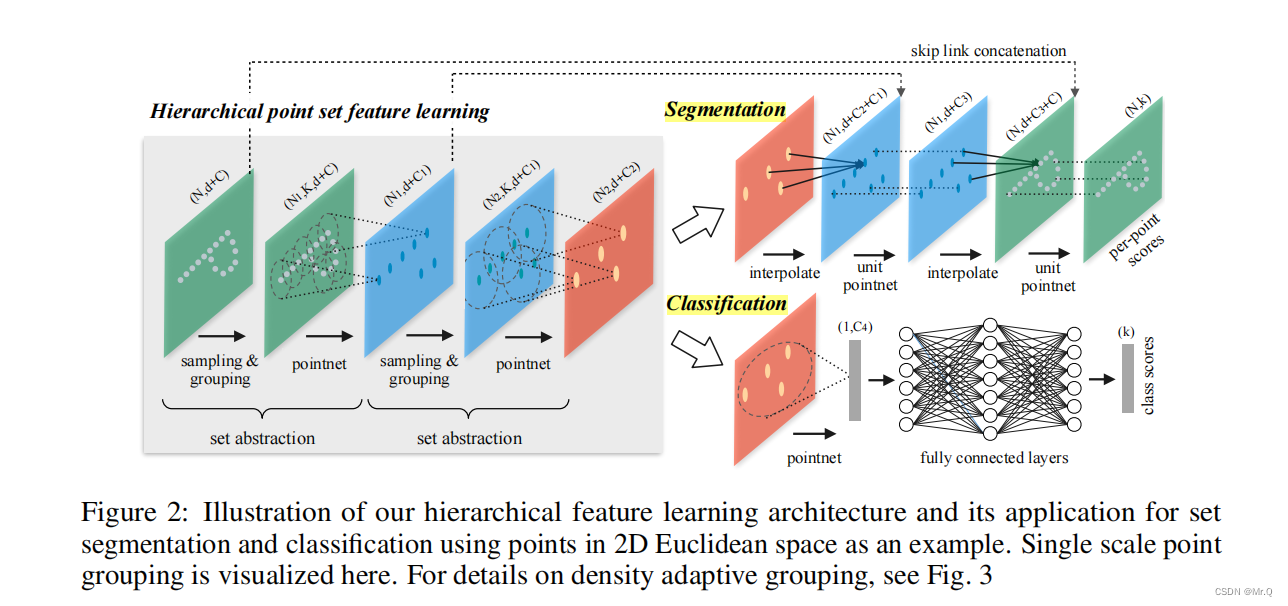
(1)pointnet++特征提取层是一个层级特征提取层,由(sampling,grouping and pointnet三个组件组成), 然后就是分割头(unet形式)和分类头(全连接层)。
(2)网络输入的是Nx(d+C)矩阵,N是点个数,d维坐标,C维点特征,输出矩阵是N'x(d+C'),其中N'是采样后的点个数,C'是点特征向量维度。
(3)每次grouping layer对局部进行KNN聚类,输入到pointnet layer再对每个cluster提取特征,这个过程相当于2D卷积操作,同样是使用层级结构,放大感受野,提取多尺度特征。
2.2 sampling layer组件
sampling layer是迭代最远距离采样IFPS算法,用采样后的点云尽可能的覆盖到原始点云所在范围,代表当前点云数据,论文中是提取1024个点,详细IFPS算法介绍可参考:
iterative farthest point sample (IFPS or FPS)-CSDN博客
如果输入Nx(d+C),则输出N'x(d+C)
2.3 grouping layer
(1)输入点集合坐标Nx(d+C)和对应的中心坐标N'xd,对每一个中心坐标利用KNN在点集合中找K个最近的点,在一个cluster中,找出的每个点维度是(d+C)特征;
(2)对于一个cluster的维度则是Kx(d+C),有N'个中心,则输出维度是N'xKx(d+C)
2.4 pointnet
(1)输入是N'xKx(d+C),有N'个聚类中心点,每个聚类中心有K个点;
(2)对每个cluster投入到pointnet层,提取特征,即Kx(d+C) -> (d+C');
(2)有N'个cluster,所以输出的是N'x(d+C')。
真正实现的时候是:(b,npoints,nsamples,features) = (b,N',K,d+C),要channel first,变成
(b,features,npoints,nsamples) = (b,d+C,N',K),比如变成(64,3,1024,16)
待续。。。
相关文章:

pointnet和pointnet++点云分割和分类
目录 1. pointnet 1.1 点云数据的特点 1.2 模型功能 1.3 网络结构 1.3.1 分类网络 1.3.2 分割网络 2. pointnet 2.1 模型 2.2 sampling layer组件 2.3 grouping layer 2.4 pointnet 1. pointnet 1.1 点云数据的特点 (1)无序性:…...

Docker-compose和Consul
目录 1、docker-compose 简介 1.1 Docker-compose 简介 2、compose 部署 2.1 Docker Compose 环境安装 2.2 YAML 文件格式及编写注意事项 * * * * 2.3 Docker Compose配置常用字段 2.4 Docker Compose 常用命令 2.5 Docker Compose 文件结构 3、Consul 3.1 什么是…...

AFL模糊测试+GCOV覆盖率分析
安全之安全(security)博客目录导读 覆盖率分析汇总 目录 一、代码示例 二、afl-cov工具下载 三、编译带覆盖率的版本并启动afl-cov 四、AFL编译插桩并运行afl-fuzz 五、结果查看 AFL相关详见AFL安全漏洞挖掘 GCOV相关详见GCOV覆盖率分析 现将两者结合,即进…...
leetcode 965.单值二叉树
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/ //遍历判断函数 bool TreeCompare(struct TreeNode* root,int x) {if(root NULL)return true;if(root->val ! x)return false…...

云计算:掌控未来,一触即发!
🎉🎉欢迎来到我的CSDN主页!🎉🎉 🏅我是尘缘,一个在CSDN分享笔记的博主。📚📚 👉点击这里,就可以查看我的主页啦!👇&#x…...
Mybatis对数据库进行增删查改以及单元测试
这篇写的草率了,是好几天前学到,以后用来自己复习 UserInfo import lombok.Data;Data public class UserInfo {private int id;private String name;private int age;private String email;//LocalDateTime可用于接收 时间}Mapper UserMapper pack…...

.bat 批处理 - 查看 MySQL 状态然后启动或关闭
我的 MySQL 服务名为 MySQL80,具体的以实际为准: echo off setlocal:check_status cls sc query MySQL80 | find "RUNNING" > nul 2>&1 if %errorlevel%0 (echo Current status of MySQL service: Running ) else (echo Current st…...

跳转传参有几种方式
在Vue Router中,实现路由跳转并传参有以下几种方式: 1. 路由参数(Route Params): 可以通过在路由配置中定义动态的占位符(即路由参数),并在跳转时通过URL路径来传递参数。这种方式适…...
DVWA靶场Medium难度部分解析
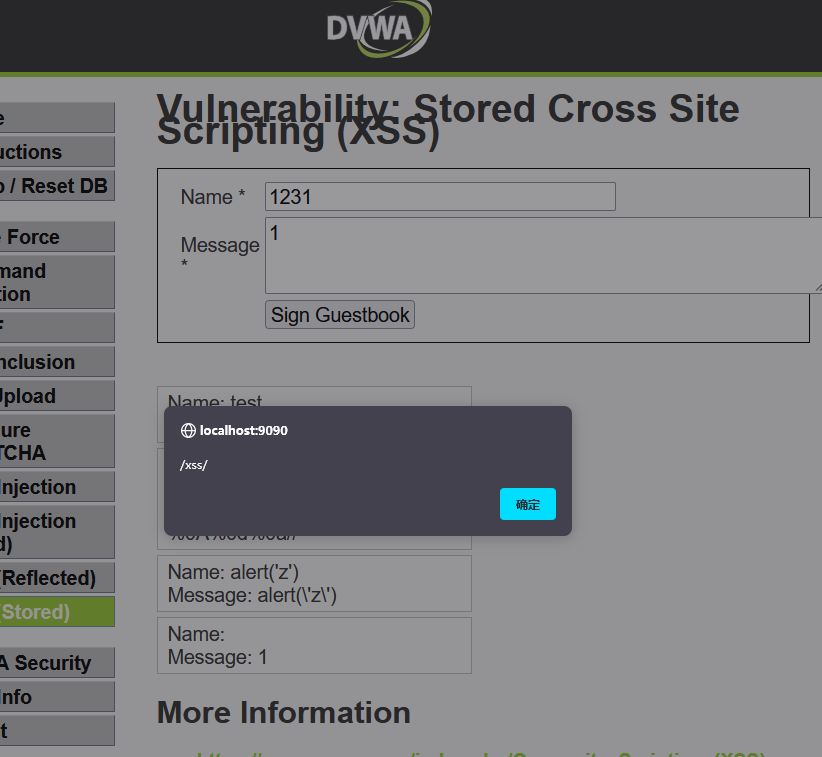
前言 好久没做题,不想吹牛逼了,消停做点题QAQ Vulnerability: Command Injection 这题不咋难,老Ping题了 输个分号ls试试,没回显即被Ban了,试试别的,例如|或者&& 出了,看看源代码 把…...

SVG图形
什么是SVG SVG(Scalable Vector Graphics)是一种用于描述二维矢量图形的XML 格式文件。它是一种用于在网络上显示图形的开放标准,旨在与Web上的其他技术(如HTML和CSS)集成,并支持在不失真的情况下缩放和调…...
冒泡排序和简答选择排序
冒泡排序 一种典型的交换排序 类似水冒泡,大元素经不断的交换由水底慢慢的浮出 从头到尾,循环比较两相邻的元素 大的元素移到后面,小的放前面-每次循环,大的元素会排到最后 代码如下: #include<stdio.h> …...
leetcode3. 无重复字符的最长子串 [滑动窗口]
题目 给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。 示例 1: 输入: s "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。示例 2: 输入: s "bbbbb" 输出: 1 解释:…...

软件工程与计算总结(十六)详细设计的设计模式
一.设计模式基础 某种意义上来说,设计模式就是设计经验的总结~ 设计模式不是简单的经验总结,更不是无中生有,它是经过实践反复检验、能解决关键技术难题、有广泛应用前景和能够显著提高软件质量的有效的经验总结。 每个模式都不是独立的&a…...

List集合拆分为多个List
list 拆分 目录概述需求: 设计思路实现思路分析1.list 拆分是2.用stream的parallel实现list的分批处理3.使用stream的parallel实现list的分批处理 参考资料和推荐阅读 Survive by day and develop by night. talk for import biz , show your perfect code,full bus…...
:MapReduce中的分区)
Hadoop3教程(十三):MapReduce中的分区
文章目录 (96) 默认HashPartitioner分区(97) 自定义分区案例(98)分区数与Reduce个数的总结参考文献 (96) 默认HashPartitioner分区 分区,是Shuffle里核心的一环…...
笔记本Win10系统一键重装操作方法
笔记本电脑已经成为大家日常生活和工作中必不可少的工具之一,如果笔记本电脑系统出现问题了,那么就会影响到大家的正常操作。这时候就可以考虑给笔记本电脑重装系统了。接下来小编给大家介绍关于一键重装Win10笔记本电脑系统的详细步骤方法。 推荐下载 系…...

FilterRegistrationBean能不能排除指定url
文章目录 什么是FilterRegistrationBean举个栗子但是如果我想要排除某些uri方法总结FilterRegistrationBean只能设置指定的url进行过滤,而不能指定排除uri,只能使用OncePerRequestFilter的shouldNotFilter方法,排除uri 什么是FilterRegistrationBean FilterRegistrationBean是…...
【LeetCode】36. 有效的数独
1 问题 请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ,验证已经填入的数字是否有效即可。 数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图&…...
华为---PPP协议简介及示例配置
PPP协议简介 PPP是Point-to-Point Protocol的简称,中文翻译为点到点协议。与以太网协议一样,PPP也是一个数据链路层协议。以太网协议定义了以太帧的格式,PPP协议也定义了自己的帧格式,这种格式的帧称为PPP帧。 利用PPP协议建立的二层网络称为…...
asp.net老年大学信息VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio计算机毕业设计
一、源码特点 asp.net老年大学信息管理系统是一套完善的web设计管理系统,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为vs2010,数据库为sqlserver2008,使用c# 语言开发 asp.net老年大学信息管理系统…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
