模型量化笔记--对称量化和非对称量化
1–量化映射
量化映射的通用公式为: r = S ( q − Z ) r = S(q - Z) r=S(q−Z)
其中r表示量化前数据的真实值,S表示缩放因子,q表示量化后的数值,Z表示零点
2–非对称量化
非对称量化需要一个偏移量Z来完成零点的映射,即量化前的零点和量化后的零点不一致。
非对称量化的一般公式为:
1.计算缩放因子S和偏移量Z
S = r m a x − r m i n q m a x − q m i n S = \frac{r_{max} - r_{min}}{q_{max} - q_{min}} S=qmax−qminrmax−rmin
Z = q m a x − R o u n d ( r m a x S ) Z = q_{max} - Round(\frac{r_{max}}{S}) Z=qmax−Round(Srmax)
r m a x r_{max} rmax和 r m i n r_{min} rmin表示真实数据的最大值和最小值, q m a x q_{max} qmax和 q m i n q_{min} qmin表示量化后的最大值和最小值,例如uint8就是127和-128。 Round()表示取整,如果是量化为int型。
2.量化
q = R o u n d ( r S + Z ) q = Round(\frac{r}{S} + Z) q=Round(Sr+Z)
3.反量化
r = ( q − Z ) ∗ S r = (q - Z)*S r=(q−Z)∗S
3–对称量化
对称量化在量化前和量化后的零点保持一致,即零点对应,因此无需像非对称量化那样引入一个偏移量Z。
对称量化的一般公式为:
1.计算缩放因子
S = ∣ r m a x ∣ ∣ q m a x ∣ S = \frac{|r_{max}|}{|q_{max}|} S=∣qmax∣∣rmax∣
2.量化
q = R o u n d ( r S ) q = Round(\frac{r}{S}) q=Round(Sr)
Round()表示取整,如果是量化为int型。
3.反量化
r = q ∗ S r = q*S r=q∗S
4–优缺点分析
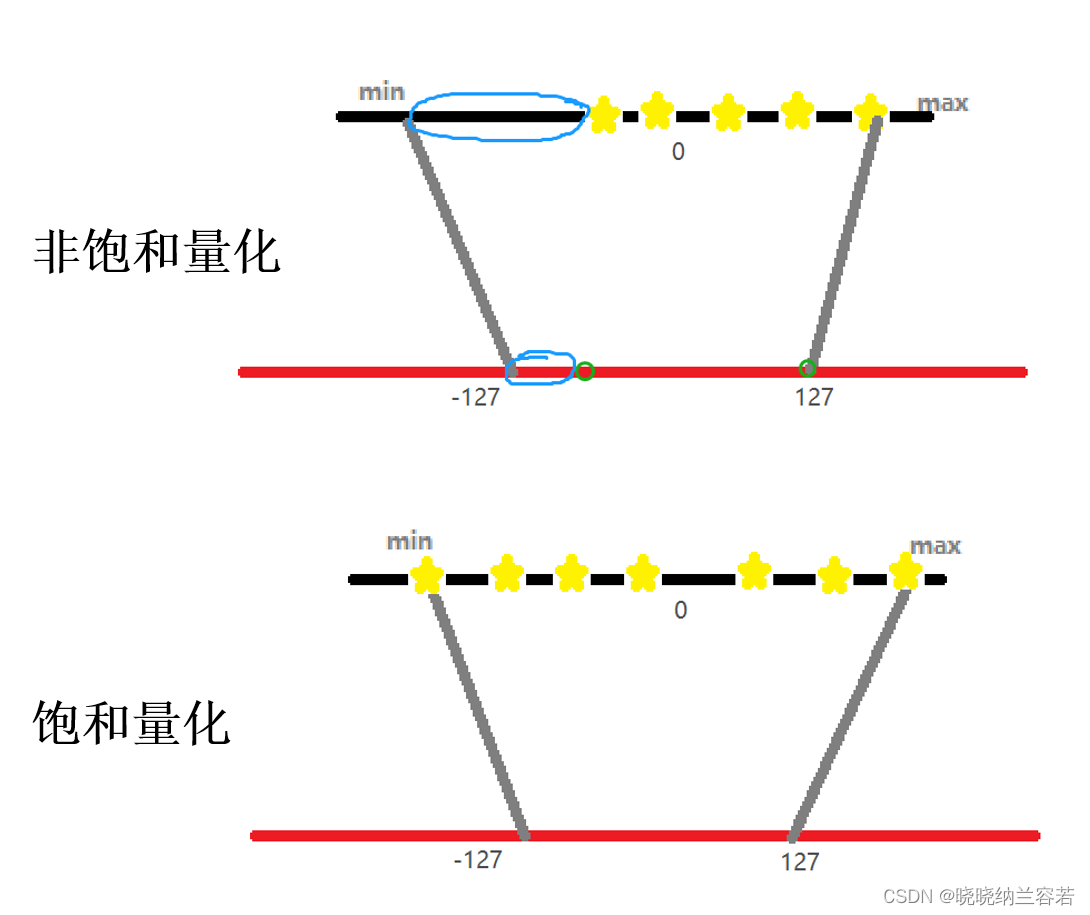
对称量化无需引入偏移量Z,因此计算量低,缺点是量化后的数据是非饱和的,即有一部分区域不存在量化的数据。非对称量化因为额外引入了一个偏移量来修正零点,因此需要的计算量会大一点。优点是其量化后的数据是饱和的,即量化前的最小值对应量化范围的最小值,量化后的最大值对应量化范围的最大值。
5–直方图过滤离散点
当数据不存在离散点时,非对称量化得到的量化数据是饱和的。但是当数据存在离散点时,量化后的数据就会分布不合理。 通过直方图可以有效过滤离散点,即在一定置信度范围内保留一定范围的数据,将范围外的数据当作离散点进行过滤。
def histgram_range(x, int_max):hist, range = np.histogram(x, 100) # 划分成100块total = len(x) # 数据量left = 0right = len(hist) - 1limit = 0.99 # 只保留99%的数据while True:cover_paecent = hist[left:right].sum() / totalif cover_paecent <= limit:break# 双指针移动elif(hist[left] <= hist[right]):left += 1else:right -= 1left_val = range[left]right_val = range[right]dynamic_range = max(abs(left_val), abs(right_val))return dynamic_range / int_max # cal scale
6–相关代码链接
对称量化和非对称量化
相关文章:

模型量化笔记--对称量化和非对称量化
1–量化映射 量化映射的通用公式为: r S ( q − Z ) r S(q - Z) rS(q−Z) 其中r表示量化前数据的真实值,S表示缩放因子,q表示量化后的数值,Z表示零点 2–非对称量化 非对称量化需要一个偏移量Z来完成零点的映射,即量化前的零…...

PA2019 Terytoria
洛谷P5987 [PA2019] Terytoria 题目大意 在一个平面直角坐标系上,有一个长度为 X X X,宽度为 Y Y Y的地图,这个地图的左边界和右边界是连通的,下边界和上边界也是连通的。 在地图中,有 X Y X\times Y XY个格子以及…...

内容分发网络CDN分布式部署真的可以加速吗?原理是什么?
Cdn快不快?她为什么会快?同样的带宽为什么她会快?原理究竟是什么,同学们本着普及知识的想法,我了解的不是很深入,适合小白来看我的帖子,如果您是大佬还请您指正错误的地方,先谢谢大佬…...
微服务docker部署实战
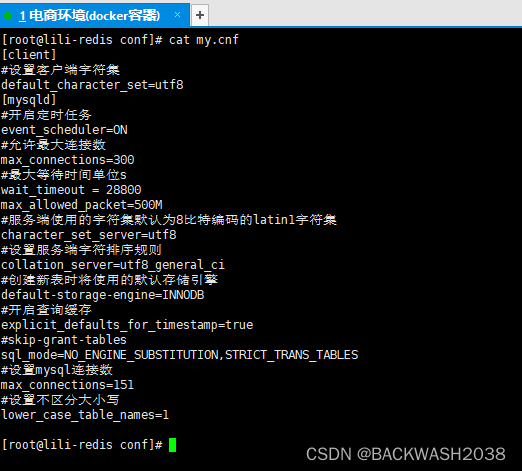
docker基础和进阶(*已掌握的可以跳过 *) 基础 docker基础 进阶 docker进阶 准备工作 提前准备好mysql和redis的配置,如下 在/zzq/mysql/conf目录下配置mysql配置文件my.cnf [client] #设置客户端字符集 default_character_setutf8 [mysqld] #开启定时任务 event_s…...

js实现拖拽功能
基于onMouseDown 、onMouseMove 、onMouseUp 使用 mousedown、mousemove 和 mouseup 事件来实现拖拽的基本思路是: 在 mousedown 事件中,开始追踪拖拽操作并记录鼠标按下的位置。 在 mousemove 事件中,根据鼠标的移动,更新被拖拽…...

数据库主从切换过程中Druid没法获取连接错误
背景: 今天dba在进行DB的主从切换,导致应用一直报错,获取不到DB连接,druid的错误信息如下: Could not open JDBC Connection for transaction; nested exception is com.alibaba.druid.pool.GetConnectionTimeoutExc…...
【iOS】Mac M1安装iPhone及iPad的app时设置问题
【iOS】Mac M1安装iPhone及iPad的app时设置问题 简介一,设置问题二,适配问题 简介 由于 苹果M1芯片的Mac可用安装iPhone以及iPad应用,因为开发者并没有适配Mac,因此产生了很多奇怪问题,这里总结归纳Mac M1安装iPhone和…...
Springboot 启动报错@spring.active@解析错误
Caused by: org.yaml.snakeyaml.scanner.ScannerException: while scanning for the next token found character that cannot start any token. (Do not use for indentation)in reader, line 10, column 13:active: spring.active^查看是否勾选...

【算法挨揍日记】day15——560. 和为 K 的子数组、974. 和可被 K 整除的子数组
560. 和为 K 的子数组 560. 和为 K 的子数组 题目描述: 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的连续子数组的个数 。 子数组是数组中元素的连续非空序列。 解题思路: 我们可以很容易想到暴力解法…...

数字时代的探索与革新:Socks5代理的引领作用
在当今快速发展的数字时代,技术创新推动着社会的变革与进步。Socks5代理作为一项重要的网络技术,正引领着跨界电商、爬虫数据分析、企业全球化和游戏体验优化等领域的发展。本文将深入探讨Socks5代理技术在这些领域中的引领作用,以及它如何塑…...
算法-堆/归并排序-排序链表
算法-堆/归并排序-排序链表 1 题目概述 1.1 题目出处 https://leetcode.cn/problems/sort-list/description/?envTypestudy-plan-v2&envIdtop-interview-150 1.2 题目描述 2 优先级队列构建大顶堆 2.1 思路 优先级队列构建小顶堆链表所有元素放入小顶堆依次取出堆顶…...
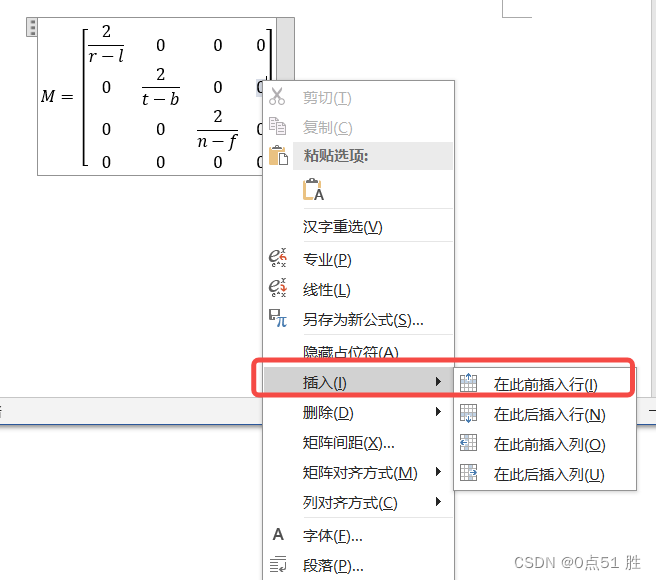
word 如何编写4x4矩阵
百度上给的教程,打印出来没有对齐 https://jingyan.baidu.com/article/6b182309995f8dba58e159fc.html 百度上的方式试了一下,不会对齐。导致公式看起来很奇怪。 下面方式会自动对齐 摸索了一下发现可以用下面这种方式编写 4x4 矩阵。先创建一个 3x3…...
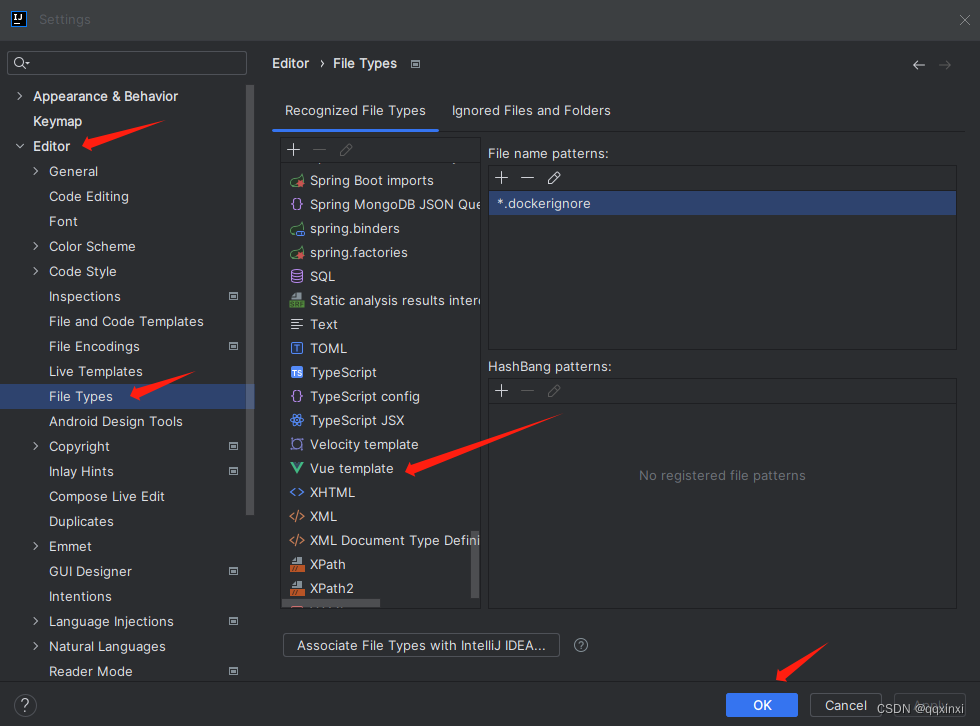
INTELlij IDEA编辑VUE项目
菜单中选择setting–>Plugins 或者快捷键 ctrlalts 搜索vue,但有些情况会搜索不出来,先说搜索到的情况 如下图所示: 如果没有vue.js则说明过去已经安装了。 搜索到了后点击Install安装即可, 但即使搜索成功了,也不…...
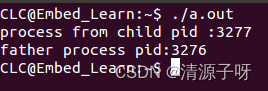
linux进程间通讯--信号量
1.认识信号量 方便理解:信号量就是一个计数器。当它大于0能用,小于等于0,用不了,这个值自己给。 2.特点: 信号量用于进程间同步,若要在进程间传递数据需要结合共享内存。信号量基于操作系统的 PV 操作&am…...

VS Code连接远程Linux服务器开发c++项目
1.在远程 Linux 上安装包 yum groupinstall "development tools" -y yum install cmake -y2.在 VSCode 上安装插件 C/CC/C Extension PackCMakeCMake ToolsCMake Language Support 3.连接远程Linux服务器...

stable diffusion的模型选择,采样器选择,关键词
一、Stable Diffusion的模型选择: 模型下载地址:https://civitai.com/,需要科学上网。 Deliberate:全能模型,prompt越详细生成的图片质量越好Realistic Vision:现实模型,生成仿真式图片&#…...

BI零售数据分析:以自身视角展开分析
随着零售业务不断扩展,市场竞争不断加剧,各层级的销售管理人员都急需一张能快速查看销售数据分析报表,能从中知道自己管辖内的业务最近或过去的情况,并依次为依据科学优化销售管理措施。这就要求零售数据分析报表信息足够多、数据…...
)
Maven 使用教程(三)
一、如何使用外部依赖项? 您可能已经注意到POM中的一个dependencies元素,我们一直在使用它作为示例。事实上,您一直在使用外部依赖项,但在这里我们将更详细地讨论它是如何工作的。有关更全面的介绍,请参阅我们的依赖机…...

行秋找工作的记录
2023-10-17 15:35-16:00 中移(苏州)研发中心面试 问了项目,还有一些我没准备到的Java八股文:Java类的加载过程,发射机制,redis存储结构,二叉平衡树等。但我也都没回答上来。应该无了。 2023-1…...
vue项目打包,使用externals抽离公共的第三方库
封装了一个插件,用来vue打包抽离公共的第三方库,使用unplugin进行插件开发,vite对应的功能使用了vite-plugin-externals进行二次开发 github地址 npm地址 hfex-auto-externals-plugin 自动注入插件,使用 unplugin 和 html-webpack-plugin进…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
