You Only Need 90K Parameters to Adapt Light 论文阅读笔记

这是BMVC2022的论文,提出了一个轻量化的局部全局双支路的低光照图像质量增强网络,有监督。
- 思路是先用encoder f(⋅)f(\cdot)f(⋅)转到raw-RGB域,再用decoder gt(⋅)g_t(\cdot)gt(⋅)模拟ISP过程转到sRGB域。虽然文章好像没有明确指出,但我看 gt(⋅)g_t(\cdot)gt(⋅)过于简单,应该是在f(⋅)f(\cdot)f(⋅)就已经进行增强了。也就是说,f(⋅)f(\cdot)f(⋅)先把暗图的sRGB转成亮图的raw-RGB,再转到sRGB域。
- gt(⋅)=(max(∑cjWci.cj(⋅),ϵ))γ,ci,cj∈{r,g,b}g_t(\cdot)=(max(\sum_{c_j}W_{c_i. c_j}(\cdot),\epsilon))^\gamma,c_i,c_j\in\{r,g,b\}gt(⋅)=(max(∑cjWci.cj(⋅),ϵ))γ,ci,cj∈{r,g,b}
- 从公式可以看出,decoder是一个3x3的矩阵WWW,这是一个简化的ISP过程,用3x3的矩阵来模拟ISP的白平衡过程,用ϵ\epsilonϵ作为下限阈值的γ\gammaγ校正来模拟ISP的非线性映射过程
- f(Ii)=Ii⊙M+Af(I_i)=I_i\odot M+Af(Ii)=Ii⊙M+A
- 从公式可以看出,encoder用element-wise的乘和加来实现逆ISP的过程,并同时对图像进行增强。
- 网络结构如下图所示:
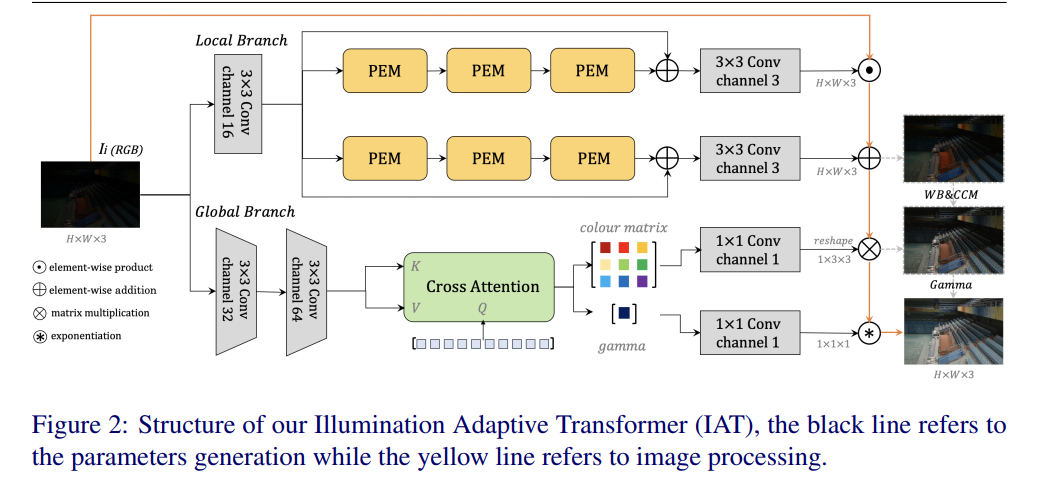
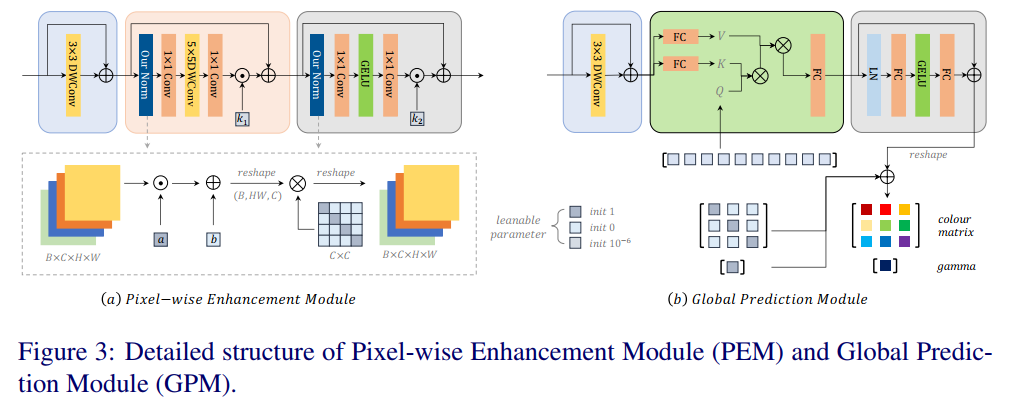
- 网络结构就不详细展开了,结果而言就是通过网络来预测上面公式中的M,A,W,γM,A,W,\gammaM,A,W,γ,来实现增强
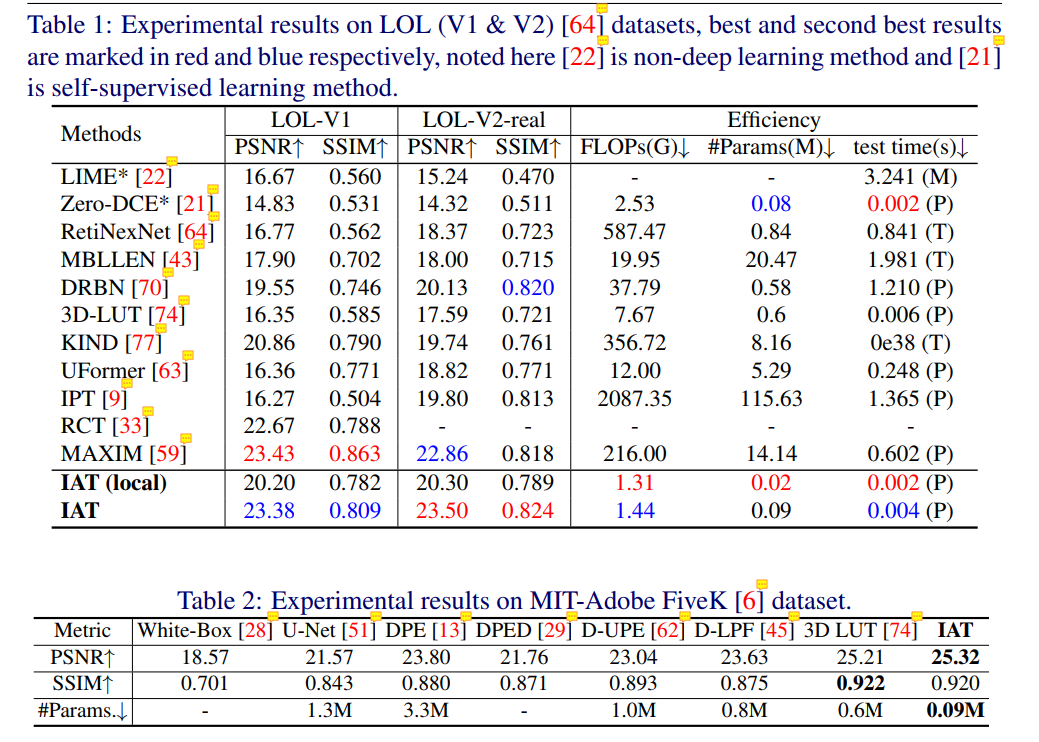
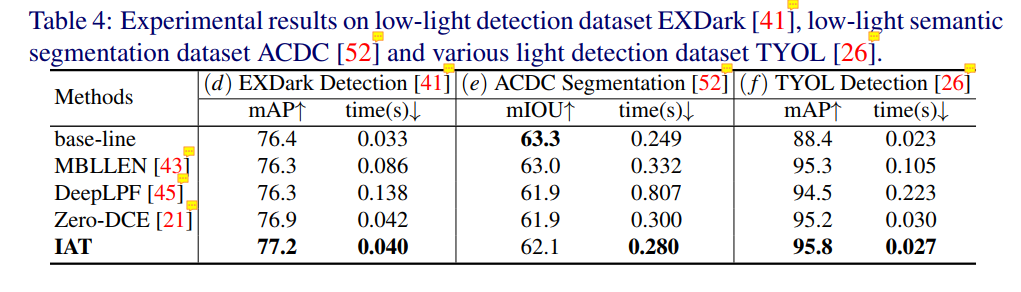
- 给出了几种实验结果,一是在LOL和fivek数据集上的对比
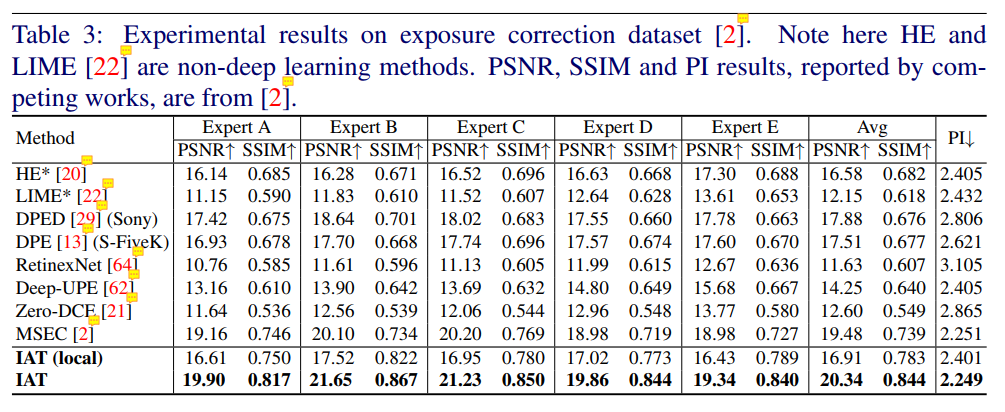
- 二是在(Learning multi-scale photo exposure correction(CVPR2021))提出的 exposure correction dataset 上对比:
- 三是在高层视觉任务上对三个黑暗图像数据集进行对比
- appendix里面给出了一些有意思的分析,和我在研究的方向几乎一致。
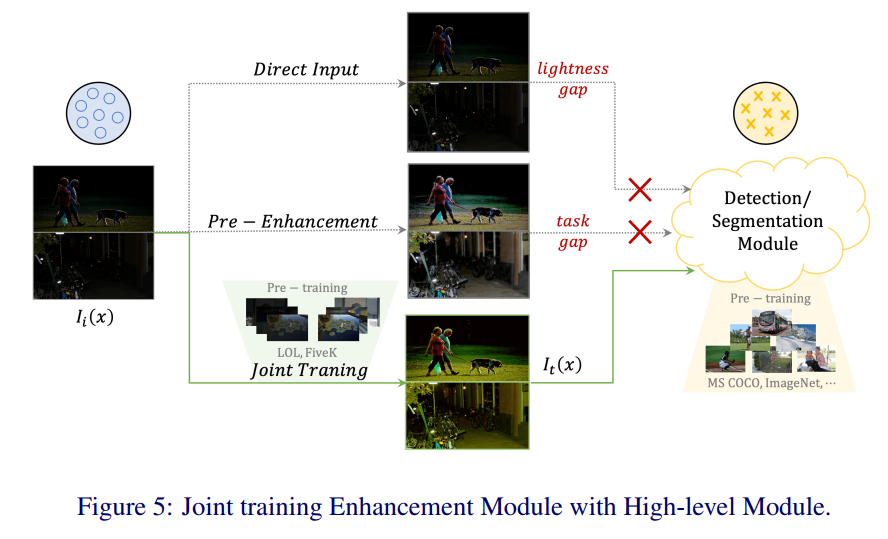
- 文章提出,直接对暗图进行增强后用训练在正常光照图像上的目标检测模型去检测会存在“target inconsistency(human vision v.s. machine vision)”,因此应该将两个网络联合训练

- 这一实验结果显示,用预训练好的网络进行joint training是更有效的方式。也就是说先在增强数据集上训练好增强网络,再和预训练好的目标检测模型一起在黑暗图像目标检测数据集上联合训练能够得到更好的结果。而我此前之所以出现不好的结果是因为我的网络是无监督网络,从而我会试图在联合训练时也为增强网络提供增强任务的损失,而文章的网络是有监督网络,它无法实现这点,但却得到了好的结果,说明联合训练时不应该提供增强任务的损失。
相关文章:

You Only Need 90K Parameters to Adapt Light 论文阅读笔记
这是BMVC2022的论文,提出了一个轻量化的局部全局双支路的低光照图像质量增强网络,有监督。 思路是先用encoder f(⋅)f(\cdot)f(⋅)转到raw-RGB域,再用decoder gt(⋅)g_t(\cdot)gt(⋅)模拟ISP过程转到sRGB域。虽然文章好像没有明确指出&…...
【vue2小知识】实现axios的二次封装
🥳博 主:初映CY的前说(前端领域) 🌞个人信条:想要变成得到,中间还有做到! 🤘本文核心:在vue2中实现axios的二次封装 目录 一、平常axios的请求发送方式 二、axios的一次封装…...

走近php的数组:数组的定义与数组函数
数组是一种数据结构,它由一组元素组成,这些元素可以是相同类型或不同类型。数组是在程序运行时动态创建的,可以根据需要增加或删除元素,因此它们是非常灵活和实用的数据结构。在大多数编程语言中,数组都有一个索引&…...
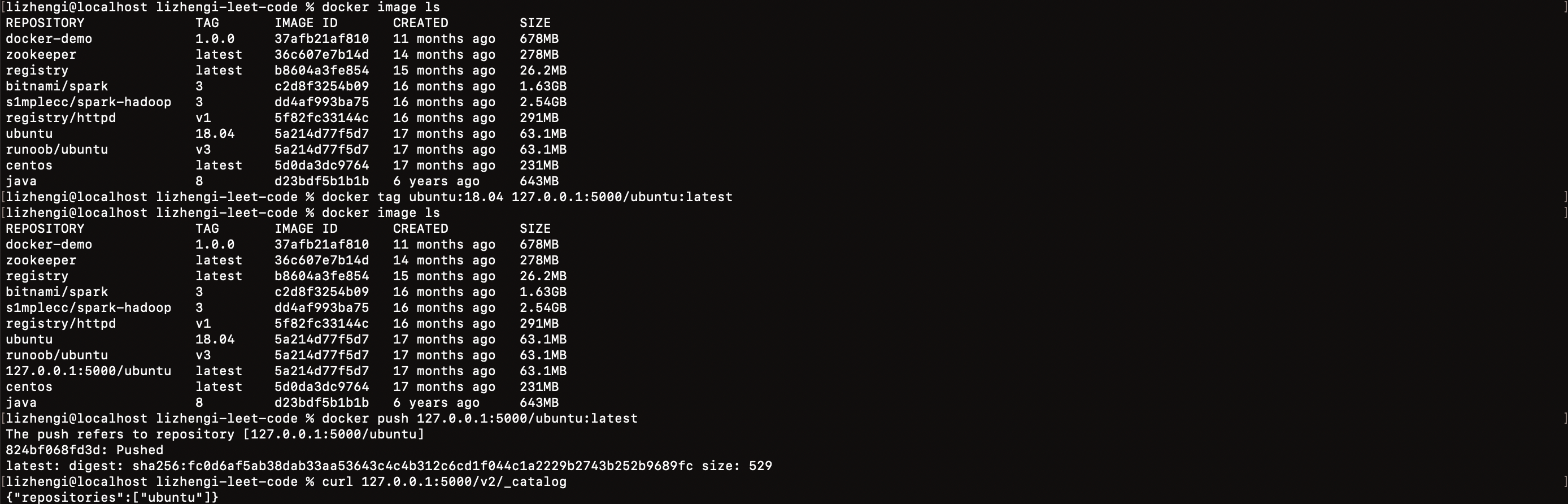
Docker 应用实践-仓库篇
目前 Docker 官方维护了一个公共仓库 Docker Hub,用于查找和与团队共享容器镜像,界上最大的容器镜像存储库,拥有一系列内容源,包括容器社区开发人员、开放源代码项目和独立软件供应商(ISV)在容器中构建和分…...
python+django篮球NBA周边商城vue
目 录 第一章 绪 论 1 1.1背景及意义 1 1.2国内外研究概况 1 1.3 研究的内容 1 第二章 关键技术的研究 3 2.1 vue技术介绍 3 myproject/ <-- 高级别的文件夹 |-- myproject/ <-- Django项目文件夹 | |-- myproje…...
抽象类与接口的区别
抽象类什么是抽象类?抽象类是特殊的类,只是不能被实例化;除此以外,具有类的其他特性;重要的是抽象类可以包括抽象方法,这是普通类所不能的。抽象方法只能声明于抽象类中,且不包含任何实现&#…...

1904. 你完成的完整对局数
题目: 一款新的在线电子游戏在近期发布,在该电子游戏中,以 刻钟 为周期规划若干时长为 15 分钟 的游戏对局。这意味着,在 HH:00、HH:15、HH:30 和 HH:45 ,将会开始一个新的对局,其中 HH 用一个从 00 到 23…...

Vue3:自定义指令以及简单的后台管理权限封装
目录 前言: 自定义指令介绍: 局部的自定义指令: 全局自定义指令: 讲讲后台管理权限管理: 前言: 说起这个自定义指令的使用场景,我第一反应就是,后台管理的权限管理,要…...
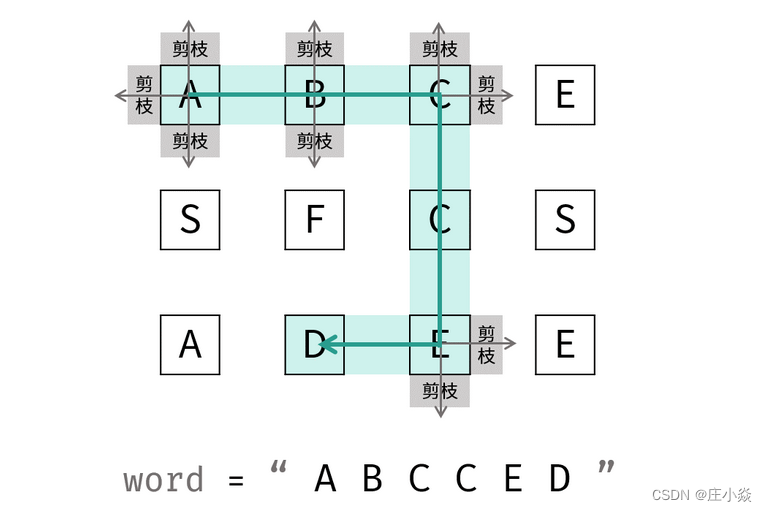
剑指 Offer 12. 矩阵中的路径
摘要 剑指 Offer 12. 矩阵中的路径 一、回溯算法解析 本问题是典型的矩阵搜索问题,可使用 深度优先搜索(DFS) 剪枝解决。 深度优先搜索: 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归,先朝一个方向搜…...
springboot+jersey+tomcat实现跨域方式上传文件到服务器
前言 在服务器上,当我们启动了tomcat,就可以以 http://ip地址:8080/文件路径/文件名 的方式,进行访问到我们服务器上处于tomcat的webapps文件夹下的文件 于是为了可以往上面加文件,我们有两种方式,一种就是直接复制文…...

【微信小程序】-- 常用视图容器类组件介绍 -- view、scroll-view和swiper(六)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &#…...
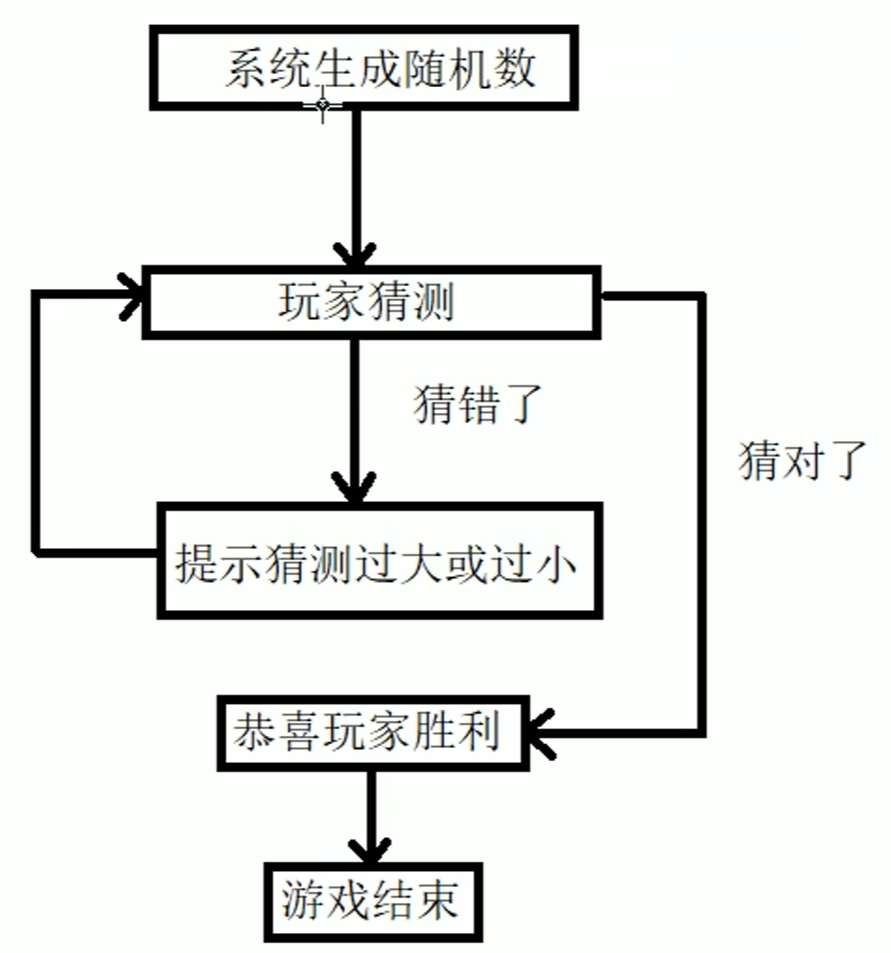
猜数字游戏——C++
我们在有了一定的C基础了以后,简单的实现一个案例(其实只要会while循环结构就行了),我们本章内容会实现猜数字游戏,大家有什么语法疑问可以看看我写的:C快速入门_染柒_GRQ的博客-CSDN博客,该博客…...

整数对最小和
题目描述 给定两个整数数组 array1 array2。数组元素按升序排列,假设从array1 、array2中分别取出一个元素可构成一对元素,现在需要取出K个元素并对取出的所有元素求和,计算和的最小值 注意事项 两对元素如果对应于array1 array2中的两个下…...

2023-2-22 -javaagent
周三,天气晴,7度 Java Agent Java Agent也叫作java探针,可以实现动态修改java字节码,完成额外的功能。在java类编译成字节码,在jvm执行之前,它可以读取修改字节码,以来完成额外的功能。 使用…...

JavaScript BOM操作
目录 前言 window 对象 location 对象 navigator 对象 screen 对象 history 对象 前言 BOM(Browser Object Model)指的是浏览器对象模型,它是 JavaScript 和浏览器之间的接口。通过 BOM,JavaScript 可以与浏览器窗口交互&…...

【机器学习 | 强基计划】开山篇 | 机器学习介绍及其类别和概念阐述
🤵♂️ 个人主页: @计算机魔术师 👨💻 作者简介:CSDN内容合伙人,全栈领域优质创作者。 机器学习 | 强基计划系列 (一) 作者: 计算机魔术师 版本: 1.0 ( 2022.2.25) 注释:文章会不定时更新补充 文章目录 前言一、机器学习概览1.1 有监督学习和无监督学习1.1.…...
)
华为OD机试真题Java实现【合规数组】真题+解题思路+代码(20222023)
合规数组 题目 给定一个正整数数组 检查数组中是否存在满足规则的数组组合 规则: A = B + 2C 🔥🔥🔥🔥🔥👉👉👉👉👉👉 华为OD机试(Java)真题目录汇总 ## 输入 第一行输出数组的元素个数 接下来一行输出所有数组元素,用空格隔开 输出 如果存在满…...

BoostSearcher搜索引擎项目
BoostSearcher搜索引擎项目 1.BoostSearcher这个项目是什么? 答:一个为Boost文档建立索引的站内搜索引擎,简单的说就是一个类似于csdn站内文档搜索框。 项目展示: gitee:https://gitee.com/zxlfx/boost-search-engine-project …...
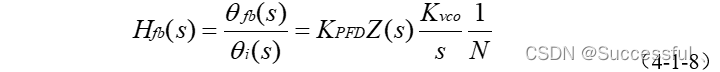
【模拟集成电路】频率综合器(Frequency Synthesizer,FS)设计
应用于无线局域网的频率综合器设计前言频率综合器简介各部分链接链接:前言 本文主要内容是对频率综合器或称为PLL 做出简单介绍,为课程设计部分章节内容,后需给出各部分的设计方案,以及测试结果。 频率综合器简介 无线收发系统中…...
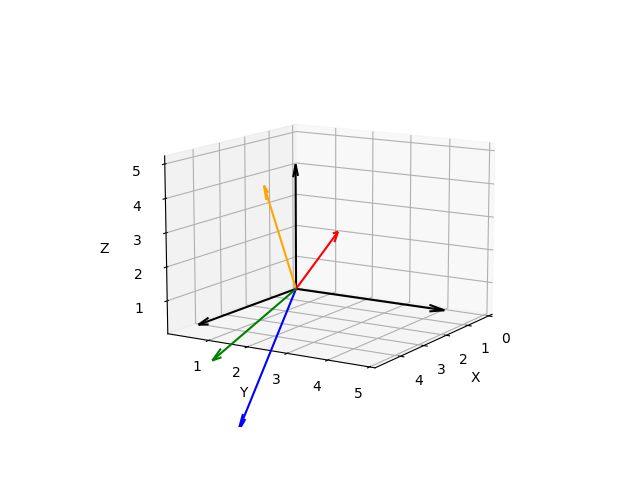
实例8:机器人的空间描述和变换仿真
实例8:机器人的空间描述和变换仿真 实验目的 通过刚体与刚体的平动、转动基础知识的学习,熟悉位姿的描述通过Python编程实践,可视化学习坐标系的变换,熟悉空间变换 实验要求 通过python编程,输入一指定向量和对应的…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
