论文笔记|固定效应的解释和使用
DeHaan E. Using and interpreting fixed effects models[J]. Available at SSRN 3699777, 2021.
虽然固定效应在金融经济学研究中无处不在,但许多研究人员对作用的了解有限。这篇论文解释了固定效应如何消除遗漏变量偏差并影响标准误差,并讨论了使用固定效应回归时的常见陷阱。特别关注在 X 变化很小或没有变化的固定效应组(例如,公司)如何混淆系数估计和解释,并且提供有关如何识别和避免上述混淆的指导。强调 FE 可以成为改进识别的强大工具,但也可能引入其自身的重要问题。更好地理解这些问题将有助于研究人员更好地选择如何设计固定效应模型并仔细解释其结果。
这里写目录标题
- Author Checklist – Good Practices when Using Fixed Effects(总结要点)
- 1. Introduction
- 1.1. How FE can eliminate omitted variables and affect standard errors
- 1.2. Problems stemming from FE groups without any variation in X
- 1.3. FE and the remaining within-group variation in X
- 1.4. Other topics
- 1.5. Contribution and limitations
- 2. Mechanics of How Fixed Effects Remove Omitted Variable Bias
- 2.1. How FE remove unobservable Z
- 2.2. What people mean by FE “restricting analysis to within-group variation”
- 2.3. Including FE for multiple groupings
- 2.4. Adding control variables \Creating finer FE groupings
- 2.6. Using FE in difference-in-differences models
- 2.7. FE when testing differences in slope coefficients (e.g., ERC regressions)
- 3. The Effects of FE on Standard Errors
- 3.1. Effect on standard errors when there are correlated omitted variables
- 3.2. Effect on standard errors when there are not correlated omitted variables
- 3.3. Standard errors in models with controls and multiple FE groupings
- 3.4. FE and clustered standard errors
- 4. Fixed Effect Groups with No Within-Group Variation in X
- 4.1. Case 1 (the easy one): fixed effect singletons
- 4.2. Case 2 (the harder one): FE groups with multiple observations but no variation in X
- 5. Fixed Effects and Remaining Within-Group Variation in X
- 5.1. How to check and report the within-group variation in X
- 5.2. Problems that can arise from eliminating a lot of variation in X
- 5.3. Interpreting coefficient magnitudes using within-group variation
- 6. Other issues and notes
- 6.1. What if Z is not actually constant within each FE group?
- 6.2. Be aware the FE can change the construct captured by X
- 6.3. R-squared in FE regressions
- 6.4. Within-FE variation in Y
- 6.5. FE and look-ahead bias
- 6.6. FE versus first-difference models
- 7. Conclusion
Author Checklist – Good Practices when Using Fixed Effects(总结要点)
- 请记住,FE只限制分析存在于FE组中的X的变化。
- 仔细考虑你是否需要FE,以及为什么:
- 如果一个不可观测的Z被认为与X和Y都相关,并且在FE组中是常数,那么包括FE可能是必要的,以减少第1类错误(弃真错误)。
2)如果未观察到的Z与Y不相关,那么FE是不必要的,并且会增加第2类错误风险(择假错误),特别是如果Z与X相关。
3)如果未观察到的Z仅与Y相关,则包括FE可以改善模型拟合并降低第2类错误的风险。
- 如果测试斜率参数的差异(例如,组间ERCs的差异),FE不能消除未观察到的Z的混淆效应,除非FE与X相互作用,这种相互作用对于高频FE通常是不切实际的,但如果忽略相互作用,则不要夸大FE对Z的控制程度。
- 报告在FE结构中存在的singleton(单例)。
1)大量的单例表明你的FE结构对你的数据来说可能太窄了。
2)考虑在样例构建期间删除单例。
3)在运行每次回归时总是删除单例。 - 报告X在FE内没有变化的观测数据的数量:
1 ) 大量FE内没有变化的观测数据引起了人们对X有变化的观测数据是否与没有变化的观测数据相似的关注。
2)评估在X中有和没有FE内变化的观测值的相似性。如果不相似,则尝试通过匹配或细化样本来提高相似性。
3)如果可能,评估有和没有无变化观测的回归结果。 - 对于非二元变量,报告X和其他关键变量的合并标准差,FE内标准差,以及FE 导致的标准差减少。
1)如果变化不大,重新考虑FE结构是否合适。 - 当使用X的标准差(或任何其他分布统计量)来解释回归系数的经济幅度时,使用FE内标准差。
1. Introduction

1.1. How FE can eliminate omitted variables and affect standard errors

1.2. Problems stemming from FE groups without any variation in X

1.3. FE and the remaining within-group variation in X

1.4. Other topics

1.5. Contribution and limitations

2. Mechanics of How Fixed Effects Remove Omitted Variable Bias


2.1. How FE remove unobservable Z
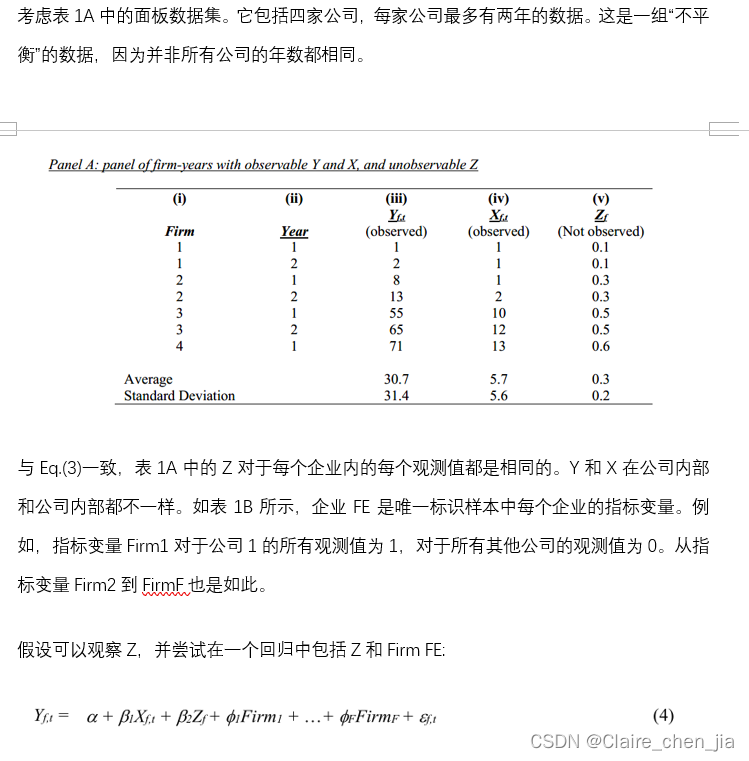
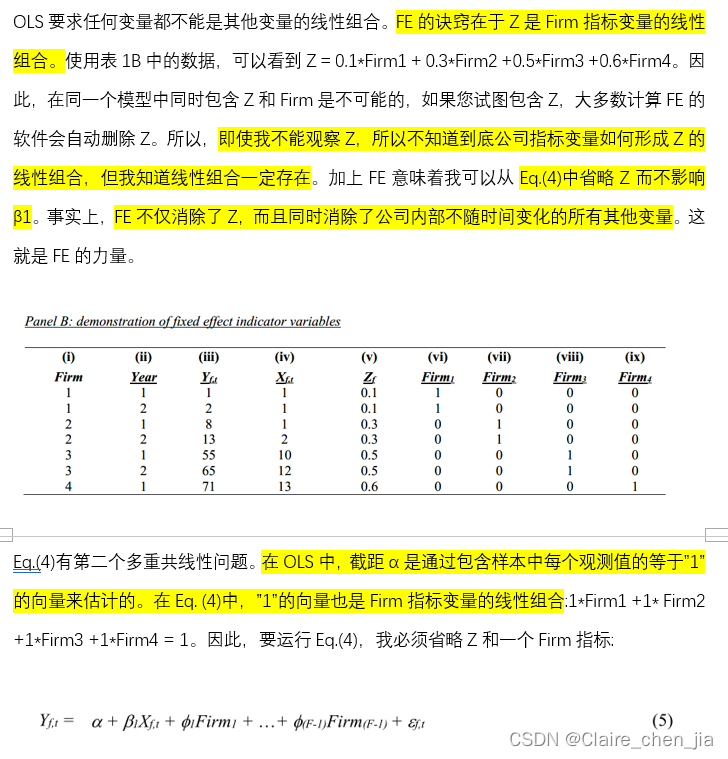

2.2. What people mean by FE “restricting analysis to within-group variation”

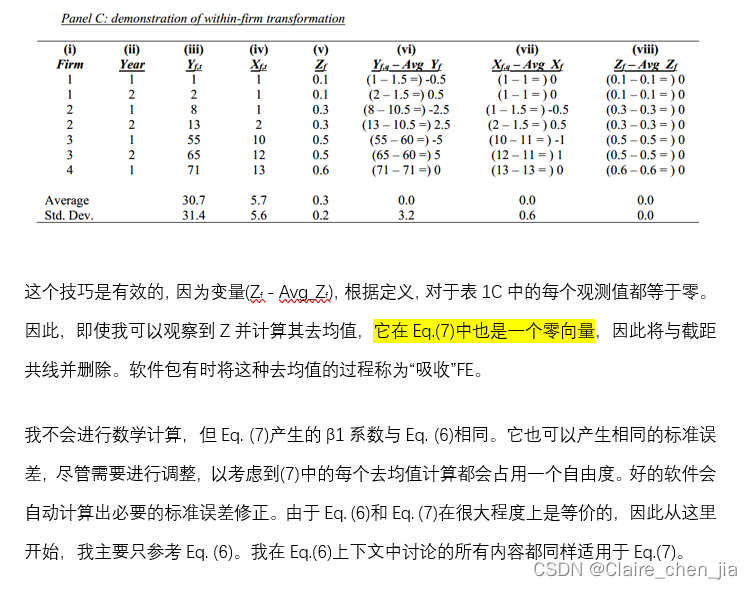
2.3. Including FE for multiple groupings

2.4. Adding control variables \Creating finer FE groupings

2.6. Using FE in difference-in-differences models


2.7. FE when testing differences in slope coefficients (e.g., ERC regressions)

3. The Effects of FE on Standard Errors
3.1. Effect on standard errors when there are correlated omitted variables



3.2. Effect on standard errors when there are not correlated omitted variables


3.3. Standard errors in models with controls and multiple FE groupings
3.4. FE and clustered standard errors

4. Fixed Effect Groups with No Within-Group Variation in X

4.1. Case 1 (the easy one): fixed effect singletons
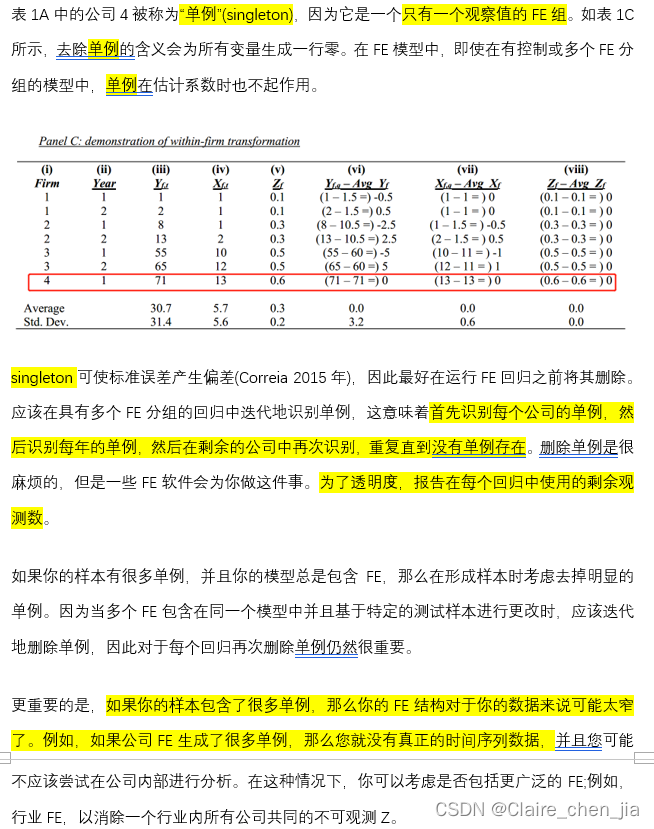
4.2. Case 2 (the harder one): FE groups with multiple observations but no variation in X
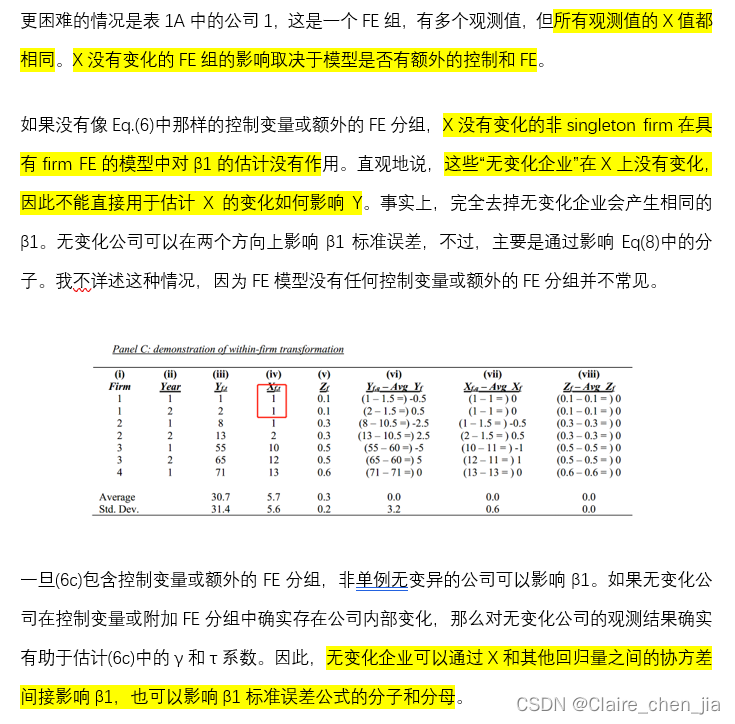






5. Fixed Effects and Remaining Within-Group Variation in X
5.1. How to check and report the within-group variation in X

5.2. Problems that can arise from eliminating a lot of variation in X


5.3. Interpreting coefficient magnitudes using within-group variation


6. Other issues and notes
6.1. What if Z is not actually constant within each FE group?
实际上,在FE组中,很少有Z是“固定的”。例如,年份FE可以保持国家GDP和失业率不变,但国内生产总值和失业率在地区层面也有所不同。或者说,2020年的苹果与2000年的苹果有很大不同。
幸运的是,FE对未观察到的Z的控制能力并非全有或全无。FE仍然可以显著地减少Z的混淆效应,这些混淆效应在每组之间只存在少量的差异。以表1C中的数据为例,如果(v)列中的Z每年变化0.01,那么(viii)列将是正负0.005的一列,而不是0的一列。并不是所有Z的变化都将被消除,但它将大大减少,因此遗漏的变量偏差也将大大减少。因此,即使在FE特性不完全固定的情况下,FE仍然可以适当地使用。这里的重要建议是不要过分依赖诸如“企业FE控制时不变的企业特征和年度FE保持不变的宏观经济条件,这是所有企业共同的”之类的陈述。仔细考虑在FE组内确实变化的相关遗漏变量仍然很重要。
6.2. Be aware the FE can change the construct captured by X
有时FE(有意或无意)会改变X捕获的结构。例如,考虑一项使用月度面板数据的研究,以调查公司的原始股票回报(X变量)是否会影响y。包括年-月FE将按月降低平均回报,这将把X从原始股票回报转化为市场调整后的异常回报。原始收益和异常收益是不同的结构,因此有和没有年-月FE的回归可以解决不同的研究问题。如果该研究的研究问题是专门关于原始收益,那么包括年-月FE可能是不合适的。
6.3. R-squared in FE regressions
FE可以解释Y的许多变化,因此可以导致调整后R2的大幅增加。因此,一些FE软件报告了“within-R2”,它表示由FE以外的解释变量产生的调整R2的一部分。
对于除了调整后的R2外,报告“within-R2”是否重要,人们意见不一。一方面,如果FE驱动几乎所有调整后的R2,这可能是潜在的问题,或者看到FE几乎没有解释能力可能是有趣的。另一方面,众所周知,在会计和财务研究中感兴趣的变量往往具有较低的解释能力(例如,Lev 1989),低调整R2本身并不一定是有效性威胁。在实践中,研究很少报告within-R2,但为了透明度,我们可能应该养成这样做的习惯,以及调整后的R2。
6.4. Within-FE variation in Y
Y没有变化的FE组确实有助于OLS中的β1,删除它们可以改变你的发现和推论。对于Y没有变化的组,Y在任何X上的回归将机械地产生β1 = 0。Y有变化的组可能有β1 > 0,合并公司将产生两个β1的加权平均值。是否去掉Y没有变化的组取决于你的研究问题的性质。如果你确实剔除了Y没有变化的FE组,你应该清楚地知道你的经验结果不能推广到这些组(即,因为已知它们的β1 = 0)。
Y没有变化的组最常见的是离散结果,如二进制或计数数据。非线性模型,如logit或Poisson可能更适合这些数据,尽管它们在使用高频FE时有缺点,并且通常不能容纳Y没有变化的FE组。在OLS与非线性模型中使用FE是一个活跃的争论,但迄今为止,大多数会计和金融研究都默认使用OLS。
只要FE组在Y上至少有一些变化,那么FE组大幅度地减少这种变化就不那么重要了,实际上可以减少标准误差。对于解释经济量级,我不知道是否以及何时使用Y的FE内标准差来这样做的指导意见。我可以想象,这样做在某些情况下是有意义的。例如,在使用国家FE的国际公司的研究中,您可能只关心存在于国家内部的Y的变化,因此可以使用Y的国内标准偏差来描述幅度。在许多其他情况下,这可能没有意义。在所有情况下,Y的FE内标准差将小于合并的标准差,因此当使用FE内变化进行描述时,幅度将显得更大。
6.5. FE and look-ahead bias
在一些研究中,尤其是那些涉及交易策略的研究中,重要的是你的模型不具有“前瞻偏差”,这意味着它们不使用在所研究的时间段内无法获得的数据。例如,如果在第t天形成对冲策略投资组合,那么交易规则不能使用直到第t天之后才可用的数据。FE很容易引起前瞻偏差。例如,在表1C中,公司内部减值计算需要两年的数据,但投资者在第一年的最后一天将没有第二年的数据。她不可能实时执行公司内部的去均值计算,因此使用公司FE会导致“前瞻偏差”。时间固定效应也有类似的问题。例如,假设有一组年度季度观测数据和一个包括年度FE的回归数据。估算年度FE需要全年的数据,而这些数据在第1、2和3季度末是不可用的。
6.6. FE versus first-difference models
“第一差分”是指将数据集转换为公司内部所有变量的周期-周期变化,是消除公司内部未观察到的常数Z的另一种方法。查看表1A,在每个公司中取第一个差值意味着(Zf,t - Zf,t-1)对于列(v)中的所有观测值都等于零,因此Zf从数据集中删除。如果每个公司只有两个观测值,则第一差分和公司FE模型产生相同的系数估计值,但在较长的面板中系数不同(一阶差分可能导致序列相关问题)。虽然FE模型在会计和金融研究中更常见,但在某些情况下,一阶差分确实有优势。有关更详细的讨论,请参阅Wooldridge(2010)。
7. Conclusion
这篇论文为使用和解释FE模型提供了一个容易理解的入门,并强调了几个问题,即使是有经验的研究人员也可能无法完全理解。对于FE的更深入研究,Wooldridge(2010)是一个很好的起点,Grieser和Hadlock(2019)深入研究了我没有涵盖的严格外生性假设,并且在整个引用中提供了对特定问题的更深入研究。我还推荐Roberts & Whited(2013)关于解决内生性问题的方法的讨论,以及Angrist & Pishke(2008)作为中级计量经济学教科书。我发现所有这些参考资料都是有用的,因为我写这个手稿。
相关文章:

论文笔记|固定效应的解释和使用
DeHaan E. Using and interpreting fixed effects models[J]. Available at SSRN 3699777, 2021. 虽然固定效应在金融经济学研究中无处不在,但许多研究人员对作用的了解有限。这篇论文解释了固定效应如何消除遗漏变量偏差并影响标准误差,并讨论了使用固…...
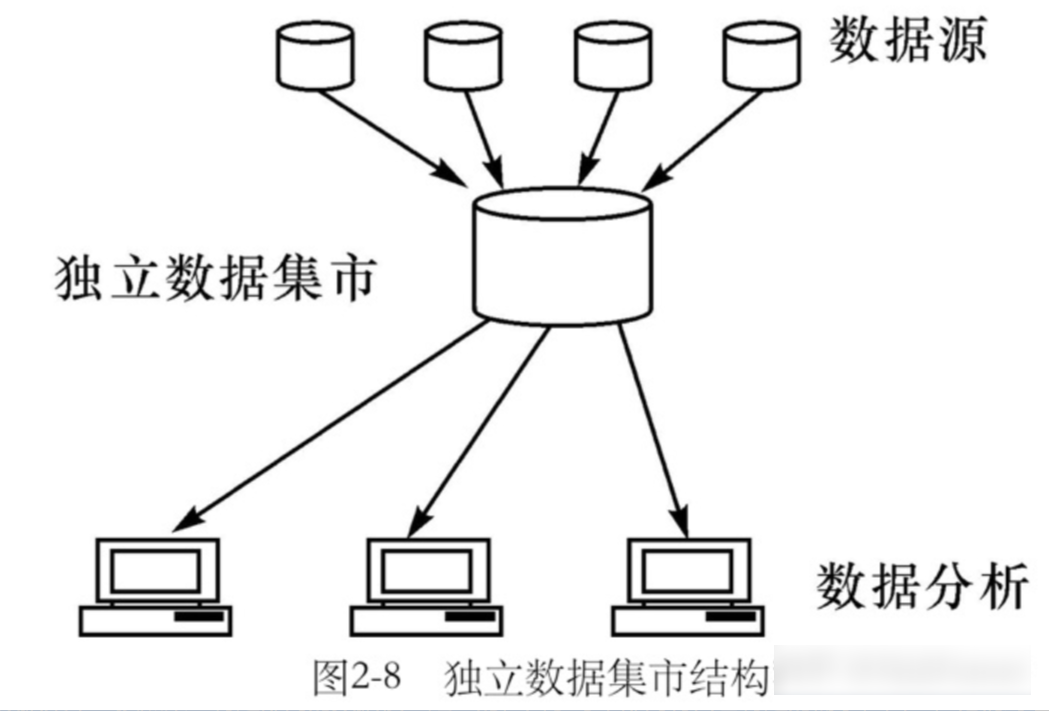
数据集市与数据仓库的区别
数据仓库是企业级的,能为整个企业各个部门的运作提供决策支持;而数据集市则是部门级的,一般只能为某个局部范围内的管理人员服务,因此也称之为部门级数据仓库。 1、两种数据集市结构 数据集市按数据的来源分为以下两种 &#x…...

Golang学习Day3
😋 大家好,我是YAy_17,是一枚爱好网安的小白。 本人水平有限,欢迎各位师傅指点,欢迎关注 😁,一起学习 💗 ,一起进步 ⭐ 。 ⭐ 此后如竟没有炬火,我便是唯一的…...
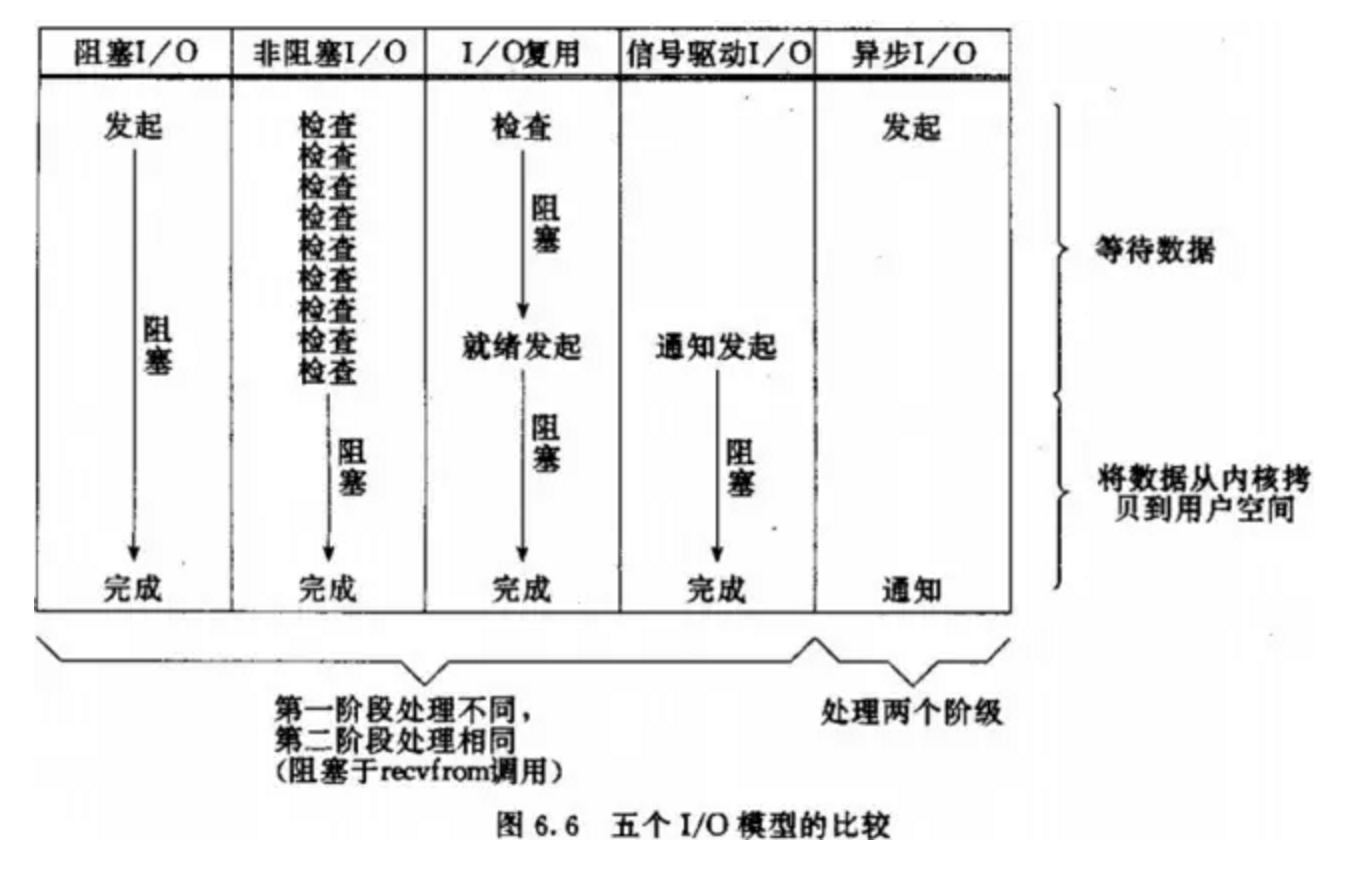
Python并发编程-事件驱动模型
一、事件驱动模型介绍 1、传统的编程模式 例如:线性模式大致流程 开始--->代码块A--->代码块B--->代码块C--->代码块D--->......---&…...
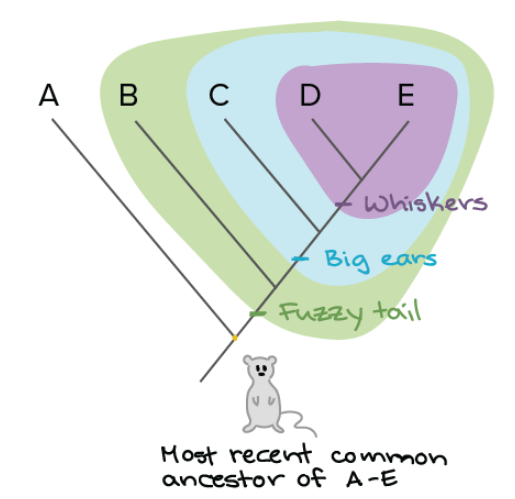
构建系统发育树简述
1. 要点 系统发育树代表了关于一组生物之间的进化关系的假设。可以使用物种或其他群体的形态学(体型)、生化、行为或分子特征来构建系统发育树。在构建树时,我们根据共享的派生特征(不同于该组祖先的特征)将物种组织成…...
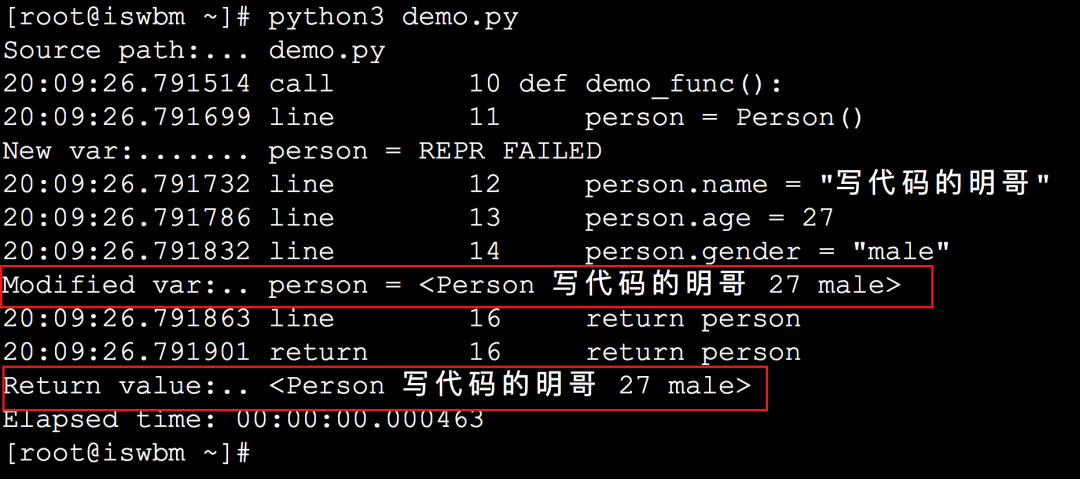
这款 Python 调试神器推荐收藏
大家好,对于每个程序开发者来说,调试几乎是必备技能。 代码写到一半卡住了,不知道这个函数执行完的返回结果是怎样的?调试一下看看 代码运行到一半报错了,什么情况?怎么跟预期的不一样?调试一…...
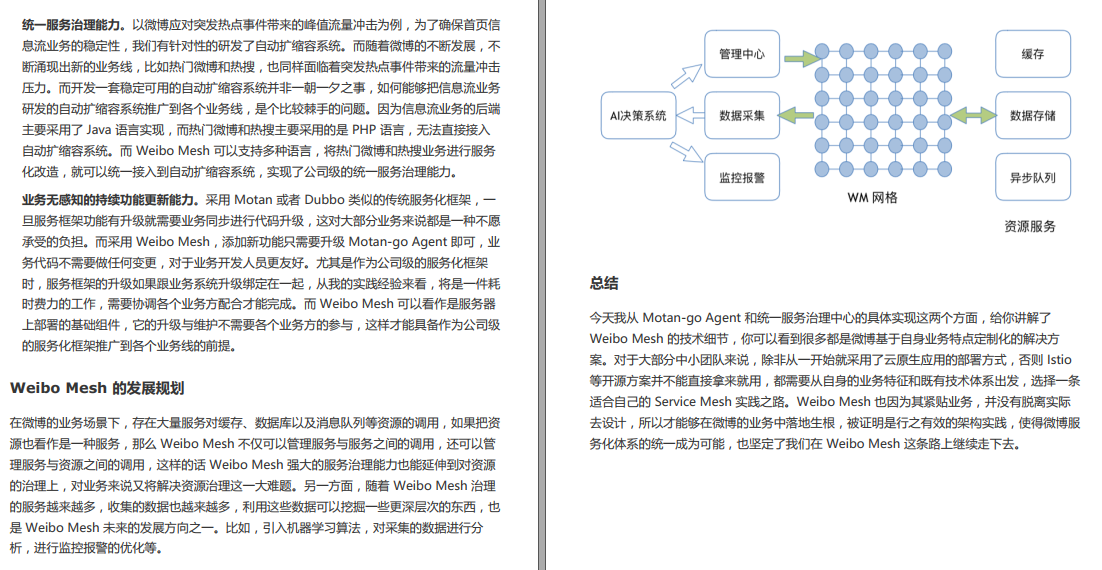
金三银四吃透这份微服务笔记,面试保准涨10K+
很多人对于微服务技术也都有着一些疑虑,比如: 微服务这技术虽然面试的时候总有人提,但作为一个开发,是不是和我关系不大?那不都是架构师的事吗?微服务不都是大厂在玩吗?我们这个业务体量用得着…...
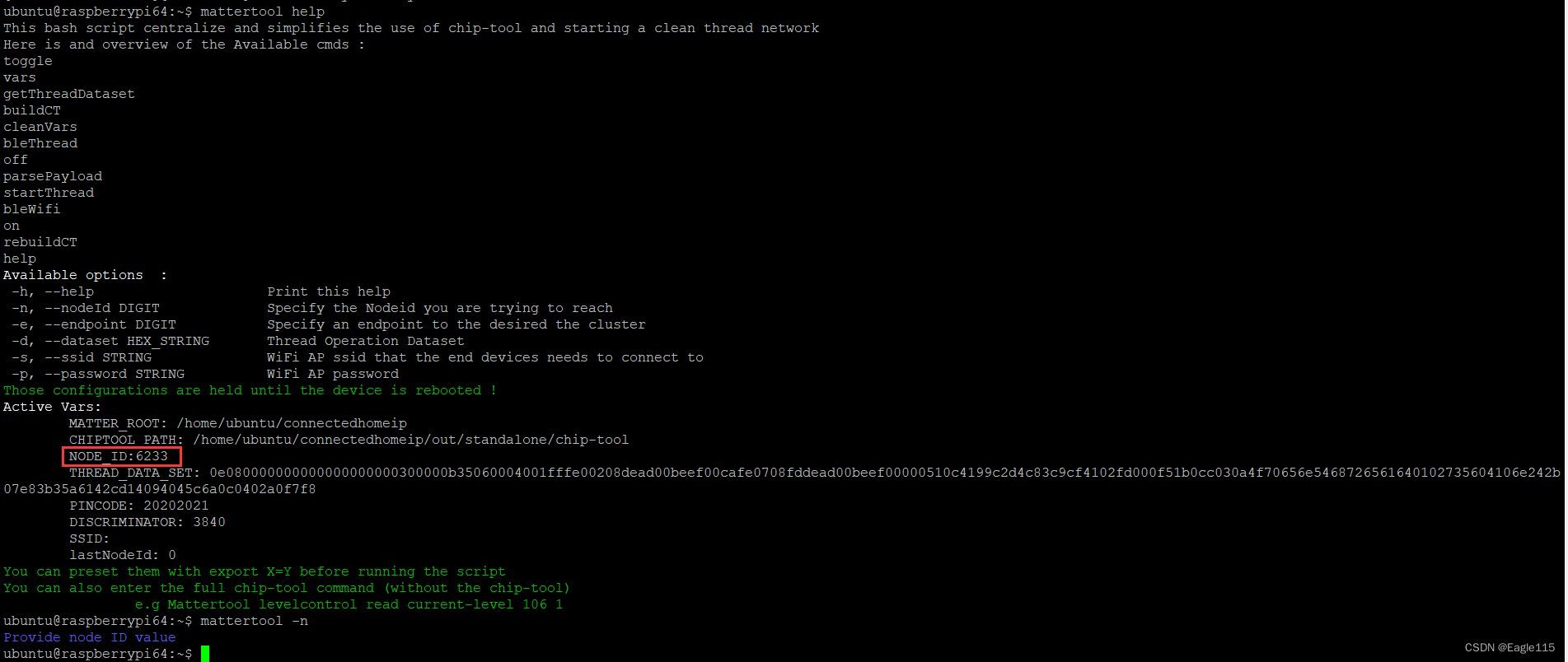
构建matter over Thread的演示系统-efr32
文章目录1. 简介2. 构建测试系统2.1设置 Matter Hub(Raspberry Pi)2.2 烧录Open Thread RCP固件2.3 烧录待测试的matter设备3. 配网和测试:3.1 使用mattertool建立Thread网络3.2 使用mattertool配置设备入网3.3 使用mattertool控制matter设备3.4 查看节点的Node ID等…...

【一天一门编程语言】Matlab 语言程序设计极简教程
Matlab 语言程序设计极简教程 用 markdown 格式输出答案。 不少于3000字。细分到2级目录。 目录 Matlab 语言程序设计极简教程 简介Matlab 工作空间Matlab 基本数据类型Matlab 语句和表达式Matlab 函数和程序Matlab 图形界面程序设计Matlab 应用实例 简介 Matlab是一种编…...
看似平平无奇的00后,居然一跃上岸字节,表示真的卷不过......
又到了一年一度的求职旺季金!三!银!四!在找工作的时候都必须要经历面试这个环节。在这里我想分享一下自己上岸字节的面试经验,过程还挺曲折的,但是还好成功上岸了。大家可以参考一下! 0821测评 …...

BZOJ2142 礼物
题目描述 一年一度的圣诞节快要来到了。每年的圣诞节小E都会收到许多礼物,当然他也会送出许多礼物。不同的人物在小E 心目中的重要性不同,在小E心中分量越重的人,收到的礼物会越多。小E从商店中购买了n件礼物,打算送给m个人 &…...
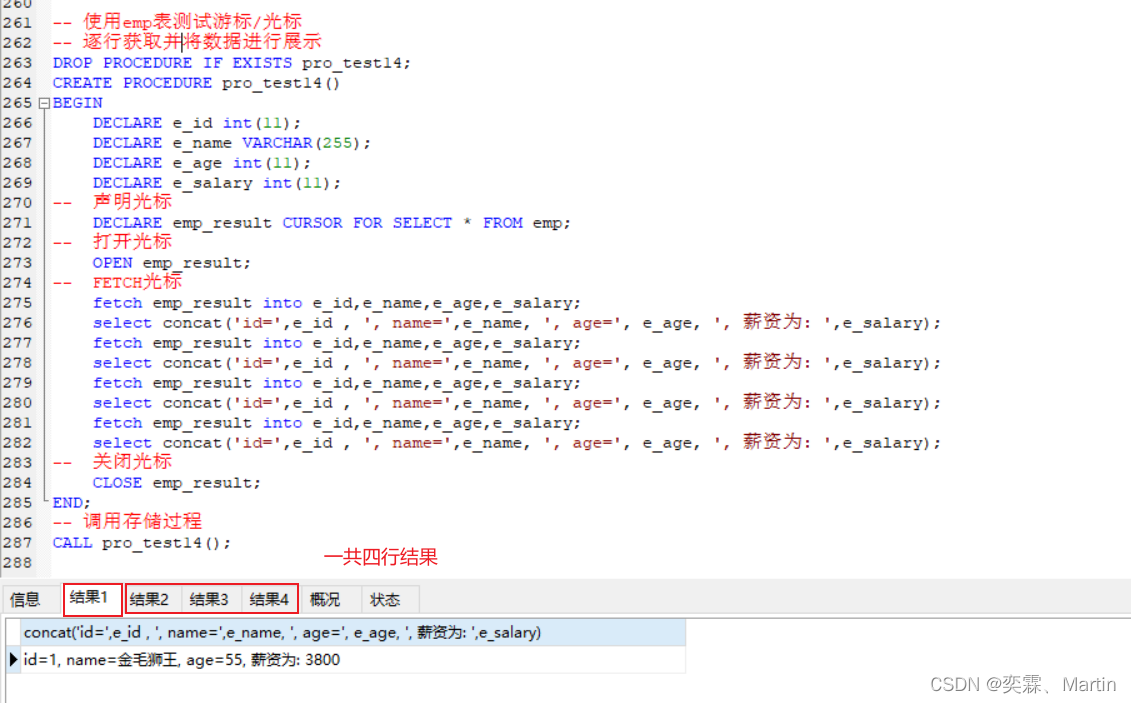
MySQL高级第一讲
目录 一、MySQL高级01 1.1 索引 1.1.1 索引概述 1.1.2 索引特点 1.1.3 索引结构 1.1.4 BTREE结构(B树) 1.1.5 BTREE结构(B树) 1.1.6 索引分类 1.1.7 索引语法 1.1.8 索引设计原则 1.2 视图 1.2.1 视图概述 1.2.2 创建或修改视图 1.3 存储过程和函数 1.3.1 存储过…...

前端面试常用内容——基础积累
1.清除浮动的方式有哪些? 高度塌陷:当所有的子元素浮动的时候,且父元素没有设置高度,这时候父元素就会产生高度塌陷。 清除浮动的方式: 1.1 给父元素单独定义高度 优点: 快速简单,代码少 缺…...
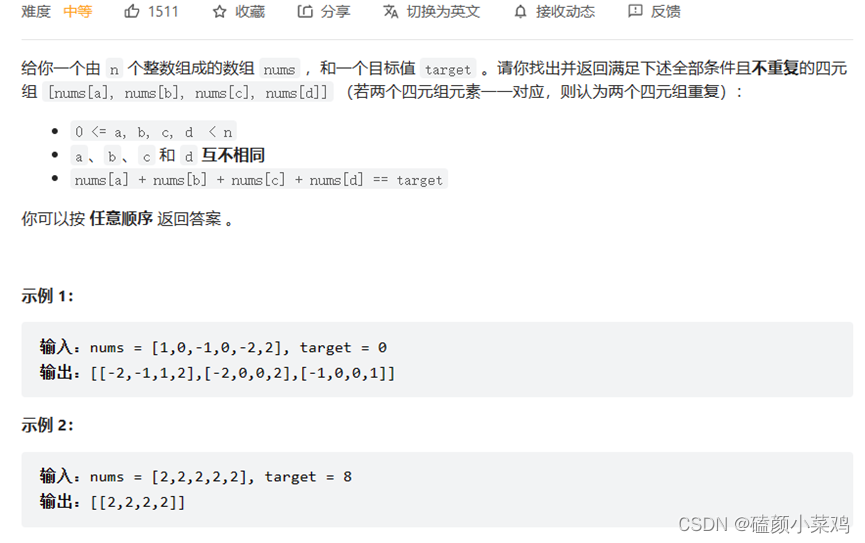
跟着《代码随想录》刷题(三)——哈希表
3.1 哈希表理论基础 哈希表理论基础 3.2 有效的字母异位词 242.有效的字母异位词 C bool isAnagram(char * s, char * t){int array[26] {0};int i 0;while (s[i]) {// 并不需要记住字符的ASCII码,只需要求出一个相对数值就可以了array[s[i] - a];i;}i 0;whi…...
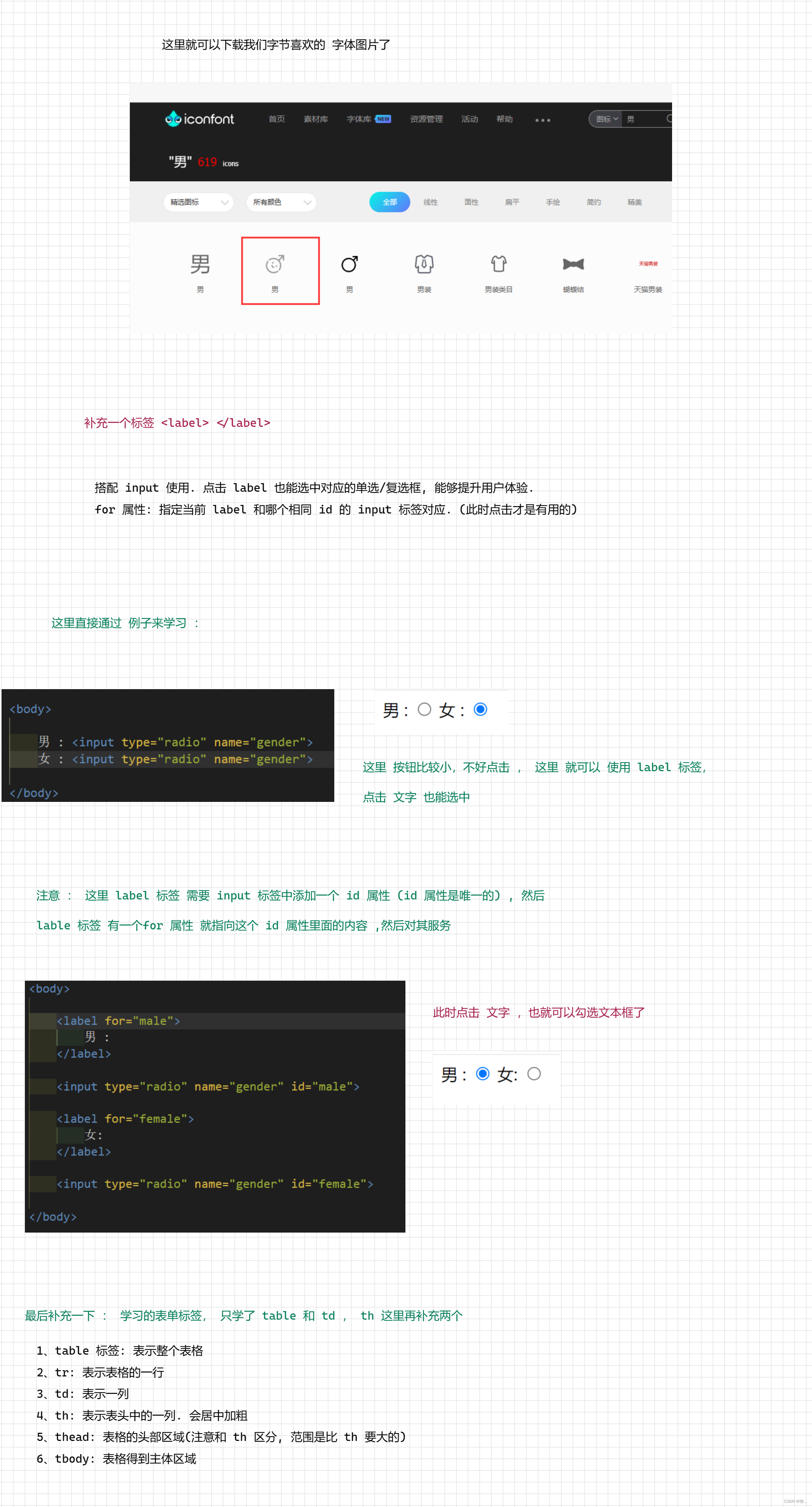
HTML - 扫盲
文章目录1. 前言2. HTML2.1 下载 vscode3 HTML 常见标签3.1 注释标签3.2 标题标签3.3 段落标签3.4 换行标签3.5 格式化标签1. 加粗2. 倾斜3. 下划线3.6 图片标签3.7 超链接标签3.8 表格标签3.9 列表标签4. 表单标签4.1 from 标签4.2 input 标签4.3 select 标签4.4 textarea标签…...
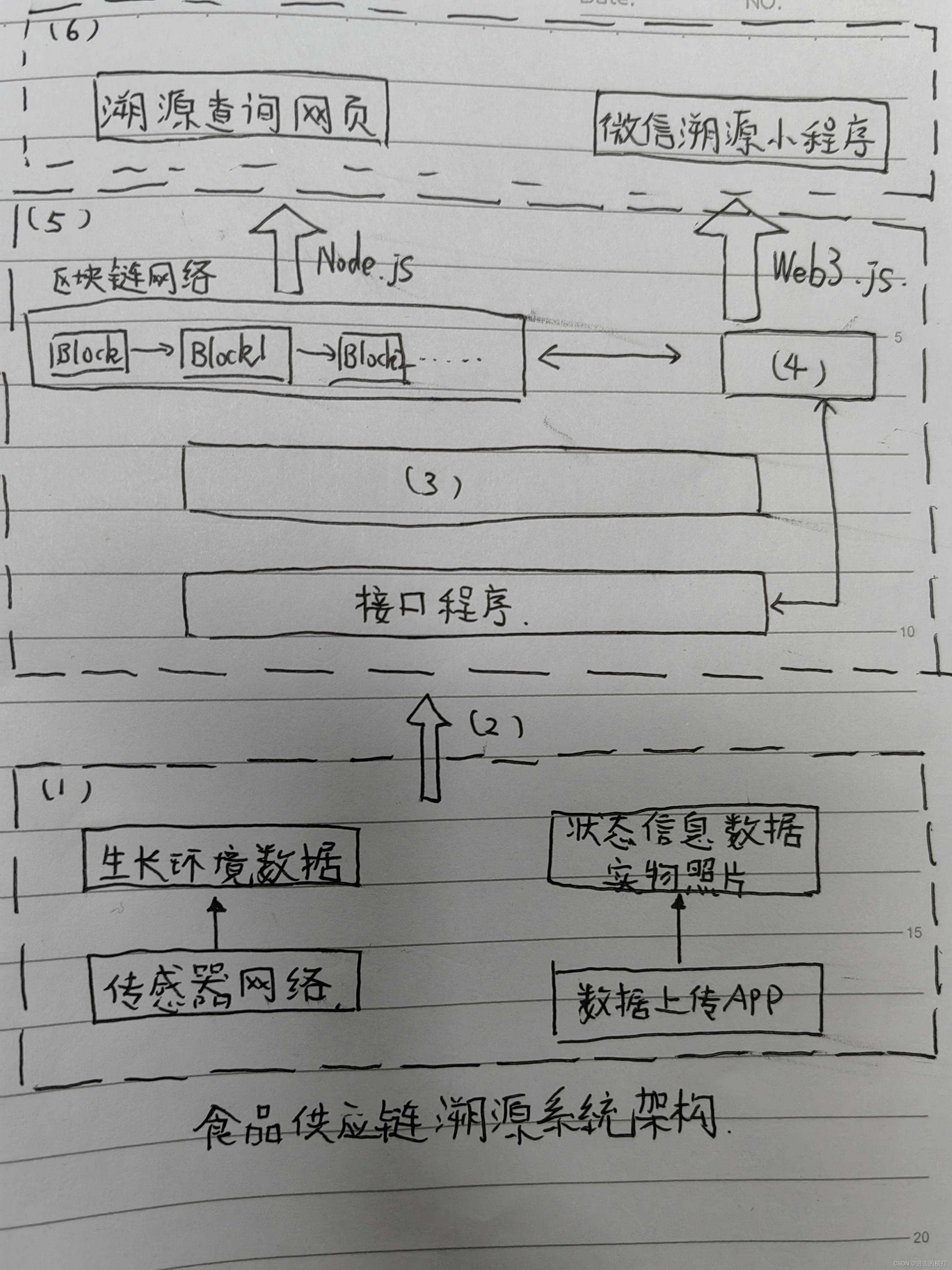
【系统分析师之路】2022上案例分析历年真题
【系统分析师之路】2022上案例分析历年真题 【系统分析师之路】2022上案例分析历年真题【系统分析师之路】2022上案例分析历年真题2022上案例分析历年真题第一题(25分)2022上案例分析历年真题第二题(25分)2022上案例分析历年真题第…...

Python编程规范
Python编程规范 当今Python编程社区有许多关于编程规范的约定和惯例。以下是一些常见的Python编程规范: 1.使用有意义的命名 使用有意义的命名可以使代码更加清晰、易读、易维护。变量、函数、类和模块的命名应该能够明确传达其用途,而不是使用无意义…...
【Java】Spring Boot项目的创建和使用
文章目录SpringBoot的创建和使用1. 什么是Spring Boot?为什么要学Spring Boot?2. Spring Boot项目的优点3. Spring Boot 项目的创建3.1 使用idea创建3.2 接下来创建Spring Boot项目4. 项目目录介绍和运行4.1 运行项目4.2 输出内容5. 总结SpringBoot的创建…...
Malware Dev 00 - Rust vs C++ 初探
写在最前 如果你是信息安全爱好者,如果你想考一些证书来提升自己的能力,那么欢迎大家来我的 Discord 频道 Northern Bay。邀请链接在这里: https://discord.gg/9XvvuFq9Wb我会提供备考过程中尽可能多的帮助,并分享学习和实践过程…...

JavaScript HTML DOM 事件
文章目录JavaScript HTML DOM 事件对事件做出反应HTML 事件属性使用 HTML DOM 来分配事件onload 和 onunload 事件onchange 事件onmouseover 和 onmouseout 事件onmousedown、onmouseup 以及 onclick 事件JavaScript HTML DOM 事件 HTML DOM 使 JavaScript 有能力对 HTML 事件做…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

python报错No module named ‘tensorflow.keras‘
是由于不同版本的tensorflow下的keras所在的路径不同,结合所安装的tensorflow的目录结构修改from语句即可。 原语句: from tensorflow.keras.layers import Conv1D, MaxPooling1D, LSTM, Dense 修改后: from tensorflow.python.keras.lay…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...

初探用uniapp写微信小程序遇到的问题及解决(vue3+ts)
零、关于开发思路 (一)拿到工作任务,先理清楚需求 1.逻辑部分 不放过原型里说的每一句话,有疑惑的部分该问产品/测试/之前的开发就问 2.页面部分(含国际化) 整体看过需要开发页面的原型后,分类一下哪些组件/样式可以复用,直接提取出来使用 (时间充分的前提下,不…...
