排序优化:如何实现一个通用的、高性能的排序函数?
文章来源于极客时间前google工程师−王争专栏。
几乎所有的编程语言都会提供排序函数,比如java中的Collections.sort()。在平时的开发中,我们都是直接使用,这些排序函数是如何实现的?底层都利用了哪种排序算法呢?
问题:如何实现一个通用的、高性能的排序函数?
如何选择合适的排序算法?
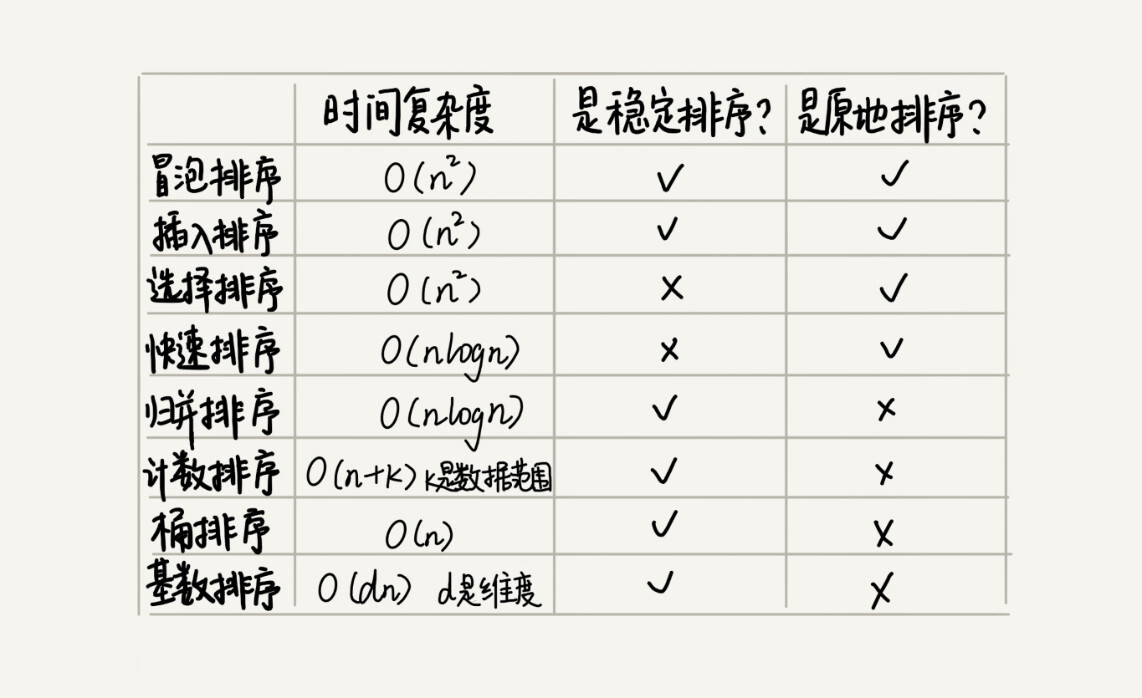
线性排序算法时间复杂度比较低,使用场景比较特殊。所以如果要写一个通用的排序函数,不能选择线性排序算法。
对于小规模数据进行排序,可以选择O(n^2)的算法;如果对大规模数据进行排序,O(nlogn)的算法更加高效。所以,为了兼顾任意规模数据的排序,一般都会首选时间复杂度为O(nlogn)的算法。
O(nlogn)的排序算法有归并排序、快速排序、还有堆排序。快排和堆排都有比较多的应用,比如java语言采用堆排序实现排序函数;c语言使用快排实现排序函数。
快排比较适合来实现排序函数,但是快排在最坏情况下时间复杂度为O(n^2),如何来解决这个“复杂度恶化”的问题呢?
如何优化快速排序?
时间复杂度退化为O(n2)的原因是,数据原来就是有序的或者接近有序的,每次分区点都选择最后一个数据。**实际上,这种O(n2)时间复杂度出现的主要原因还是因为我们分区点选的不够合理。**
最理想的分区点是:被分区点分开的两个分区中,数据的数量差不多。
为了提高排序算法的性能,我们也要尽可能地让每次分区都比较平均。
比较常用、简单的分区算法:
1.三数取中法
从区间的首、尾、中间取出一个数,然后对比大小,取这3个数的中间值作为分区点。如果排序的数组比较大,那么“三数取中”可能就不够了,可能要“五数取中”或者“十数取中”。
2.随机法
从排序区间中随机选择一个元素作为分区点。
快排是用递归来实现的。递归要警惕堆栈溢出。
- 限制递归深度,设定阈值,超过就停止递归。
- 堆上模拟实现一个函数调用栈,手动模拟递归压栈、出栈过程,这样就没有了系统栈大小的限制。
举例分析排序函数
C语言中的qsort()函数。源码解析:
qsort()优先使用归并排序来排序输入数据,归并排序空间复杂度为O(n),对于小数据量的排序,比如1KB、2KB等,归并排序额外需要1KB、2KB的内存空间,问题不大。空间换时间思想。
如果数据量太大,比如100MB,归并排序就不合适了。所以,当数据量比较大的时候,qsort()会改用快速排序算法来排序。qsort()选择分区点的方法就是“三数取中法”
递归太深导致堆栈溢出的问题,qsort()通过自己实现一个堆上的栈,手动模拟递归来解决。
qsort()不仅仅用到了归并排序和快速排序,它还用了插入排序。排序过程中,当要排序的区间中,元素的个数小于等于4,qsort()就退化为插入排序,不再继续用递归来做快速排序。在小规模数据面前,O(n^2)时间复杂度的算法并不一定比O(nlogn)的算法执行时间长。
复杂度分析比较偏理论,深究的话,实际上时间复杂度并不等于代码实际的运行时间。
如果不省略低阶、系数和常数。O(nlogn) = O(knlogn+c)
假设K=1000,c=200,当我们对小规模数据(n=100)排序,n^2实际上比Knlogn+c还要小。
knlogn+c = 1000 * 100 * log100 + 200 远大于 10000n^2 = 100*100 = 10000qsort()插入排序的算法实现中,使用哨兵编程技巧,虽然哨兵可能只是少做一次判断,但毕竟排序函数是非常常用、基础的函数,性能优化要做到极致。
总结
大部分排序函数都是采用O(nlogn)排序算法实现,但是为了尽可能提高性能,会做很多优化。
排序中的优化策略,比如合理选择分区点、避免递归太深等。
思考
学习Arrays.sort()源码
相关文章:

排序优化:如何实现一个通用的、高性能的排序函数?
文章来源于极客时间前google工程师−王争专栏。 几乎所有的编程语言都会提供排序函数,比如java中的Collections.sort()。在平时的开发中,我们都是直接使用,这些排序函数是如何实现的?底层都利用了哪种排序算法呢? 问题…...
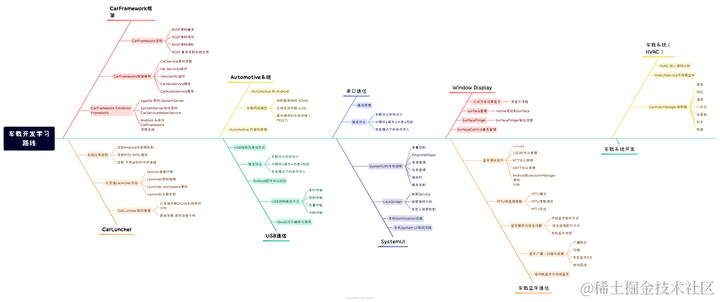
车载开发学习——CAN总线
CAN总线又称为汽车总线,全程为“控制器局域网(Controller Area Network)”,即区域网络控制器,它将区域内的单一控制单元以某种形式连接在一起,形成一个系统。在这个系统内,大家以一种大家都认可…...

2023年知名国产数据库厂家汇总
随着信创国产化的崛起,大家纷纷在寻找可替代的国产数据库厂家。这里小编就给大家汇总了一些国内知名数据库厂家,仅供参考哦! 2023年知名国产数据库厂家汇总 1、人大金仓 2、瀚高 3、高斯 4、阿里云 5、华为云 6、浪潮 7、达梦 8、南大…...

【ARM Coresight SoC-400/SoC-600 专栏导读】
文章目录 1. ARM Coresight SoC-400/SoC-600 专栏导读目录1.1 Coresight 专题1.1.1 Performance Profiling1.1.2 ARM Coresight DS-5 系列 1. ARM Coresight SoC-400/SoC-600 专栏导读目录 本专栏全面介绍 ARM Coresight 系统 及SoC-400, SoC-600 中的各个组件。 1.1 Coresigh…...

在Go中创建自定义错误
引言 Go提供了两种在标准库中创建错误的方法,[errors.New和fmt.Errorf],当与用户交流更复杂的错误信息时,或在调试时与未来的自己交流时,有时这两种机制不足以充分捕获和报告所发生的情况。为了传达更复杂的错误信息并实现更多的…...
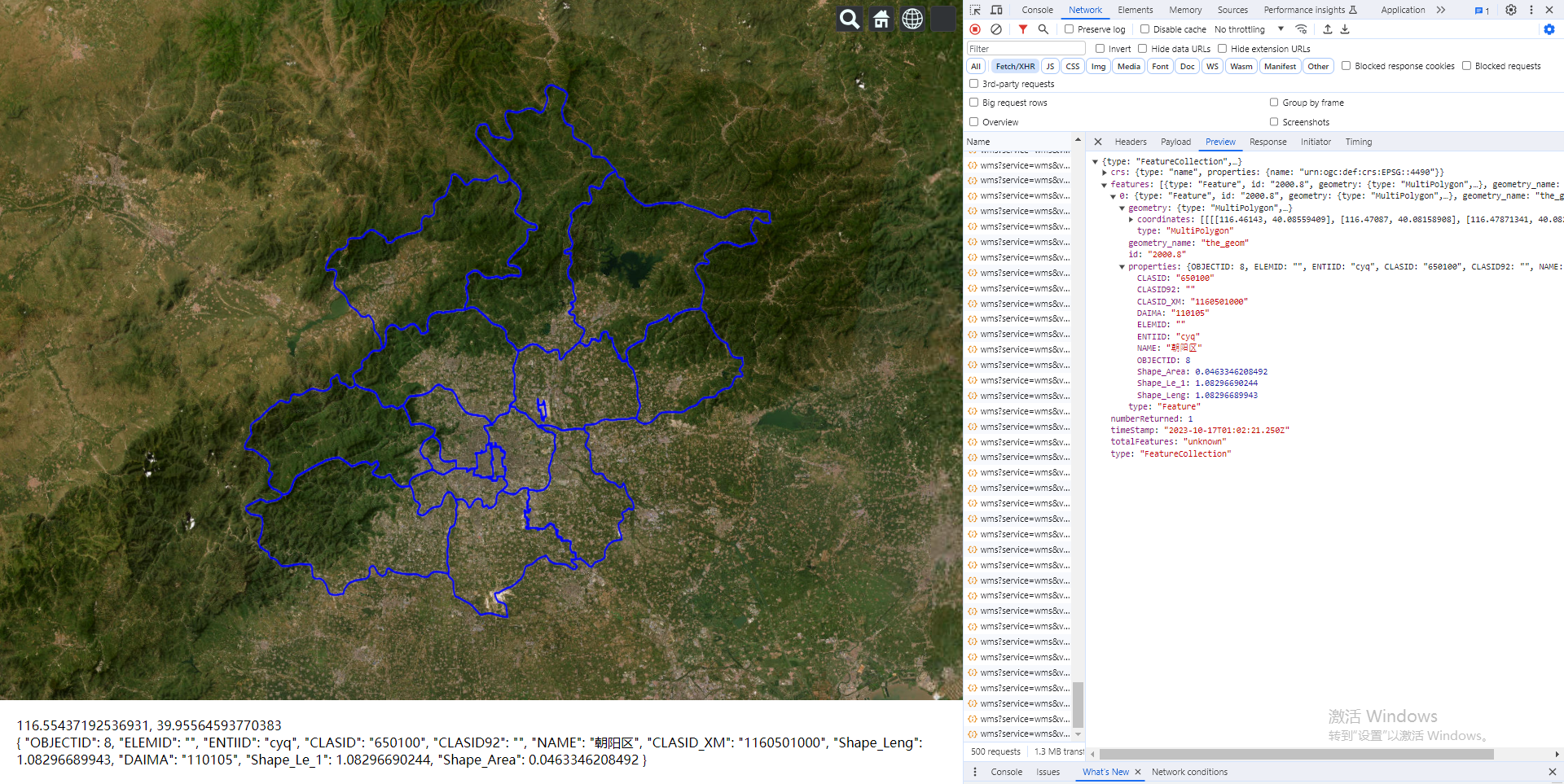
Vue.js2+Cesium1.103.0 十三、通过经纬度查询 GeoServer 发布的 wms 服务下的 feature 对象的相关信息
Vue.js2Cesium1.103.0 十三、通过经纬度查询 GeoServer 发布的 wms 服务下的 feature 对象的相关信息 Demo <template><divid"cesium-container"style"width: 100%; height: 100%;"><div style"position: absolute;z-index: 999;bott…...
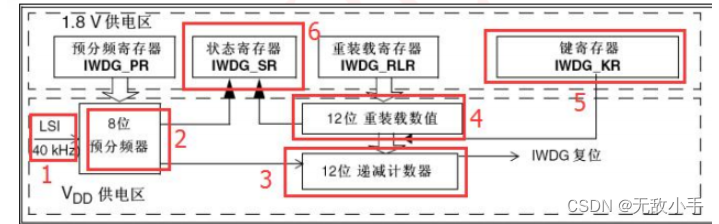
使用STM32怎么喂狗 (IWDG)
STM32F1 的独立看门狗(以下简称 IWDG)。 STM32F1内部自带了两个看门狗,一个是独立看门狗 IWDG,另一个是窗口看门狗 WWDG, 本章只介绍独立看门狗 IWDG,窗口看门狗 WWDG 会在后面章节介绍。 本章要实现的功能…...
GEE:计算和打印GEE程序的执行时间
作者:CSDN @ _养乐多_ 本文记录了计算和打印程序的执行时间的Google Earth Engine (GEE)代码,并举例说明。 大家在执行GEE代码的时候,有时候为了对比两个不同的脚本,不知道代码执行花费了多少时间。本文记录了打印代码执行时间的函数,并举了一个应用案例说明。可以知道…...
GDPU 数据结构 天码行空5
一、实验目的 1.掌握队列的顺序存储结构 2.掌握队列先进先出运算原则在解决实际问题中的应用 二、实验内容 仿照教材顺序循环队列的例子,设计一个只使用队头指针和计数器的顺序循环队列抽象数据类型。其中操作包括:初始化、入队…...

SQLAlchemy学习-12.查询之 order_by 按desc 降序排序
前言 sqlalchemy的query默认是按id升序进行排序的,当我们需要按某个字段降序排序,就需要用到 order_by。 order_by 排序 默认情况下 sqlalchemy 的 query 默认是按 id 升序进行排序的 res session.query(Project).all() print(res) # [<Project…...

如何轻松打造数字人克隆系统+直播系统?OEM教你快速部署数字人SaaS系统源码
数字人做为国内目前最热门的人工智能创业赛道,连BAT都在跑步入局,中小企业更是渴望不渴及。但随着我国数字人头部品牌企业温州专帮信息科技有限公司旗下灰豚AI数字人平台的开源。使得中小企业零门槛可以轻松打造灰豚AI数字人一模一样的平台。灰豚数字人A…...
药物滥用第四篇介绍
OXY: 羟考酮(Oxycodone,OXY),分子式为C18H21NO4,是一种半合成的蒂巴因衍生物。羟考酮为半合成的纯阿片受体激动药,其作用机制与吗啡相似,主要通过激动中枢神经系统内的阿片受体而起镇…...

Apache Doris (四十三): Doris数据更新与删除 - Update数据更新
🏡 个人主页:IT贫道_大数据OLAP体系技术栈,Apache Doris,Clickhouse 技术-CSDN博客 🚩 私聊博主:加入大数据技术讨论群聊,获取更多大数据资料。 🔔 博主个人B栈地址:豹哥教你大数据的个人空间-豹哥教你大数据个人主页-哔哩哔哩视频 目录 1. Update数据更新原理...
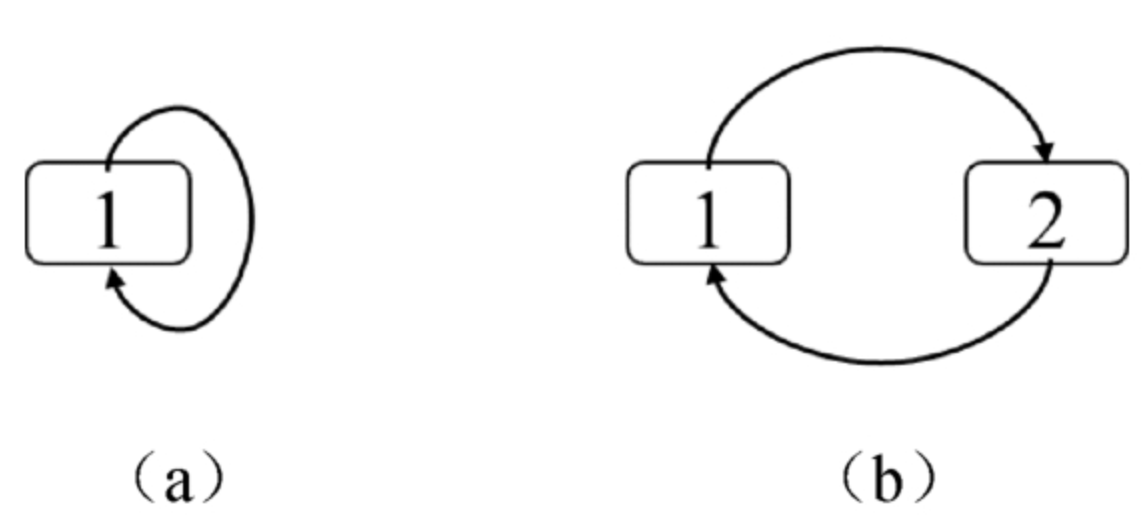
面试算法29:排序的循环链表
问题 在一个循环链表中节点的值递增排序,请设计一个算法在该循环链表中插入节点,并保证插入节点之后的循环链表仍然是排序的。 分析 首先分析在排序的循环链表中插入节点的规律。当在图4.15(a)的链表中插入值为4的节点时&…...
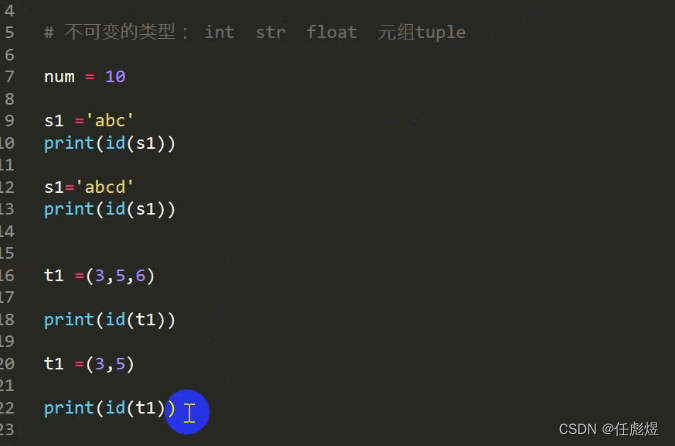
python中不可变类型和可变类型
不可变类型:修改之后内存存储地址不会发生改变 可变类型:修改之后内存存储地址发生改变 set...

vue3封装Axios库的 API 请求并使用拦截器来处理请求和响应
目录 为什么添加封装该部分? 具体代码: 对代码的解释: 如何使用? 为什么添加封装该部分? 简化发送 HTTP 请求的流程提供统一的错误处理机制支持用户状态管理和鉴权具备良好的扩展性和灵活性提高开发效率并使得代码…...

RK3588开发笔记(二):基于方案商提供sdk搭建引入mpp和sdk的宿主机交叉编译Qt5.12.10环境
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/133915614 红胖子网络科技博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV、OpenGL、ffmpeg、OSG、单片机、软硬…...

rust学习——函数返回值
概念 Rust 中的函数定义以 fn 开始,后跟着函数名和一对圆括号。大括号告诉编译器函数体在哪里开始和结束。 特殊的地方——函数返回值 错误的写法 正解1 去掉分号 fn main() {let x plus_one(5);println!("The value of x is: {}", x); }fn plus_…...

【Cadence】配置文件cdsinit和cdsenv的使用
文件功能 .cdsinit文件:主要负责一些加载项的设置,一些脚本工具及一些快捷键 .cdsenv文件:主要负责一些环境变量或者参数的设置 文件位置: (参照以下文件使用) Virtuoso配置文件“.cdsenv”文件介绍和使…...
)
软考 系统架构设计师系列知识点之基于架构的软件开发方法ABSD(6)
接前一篇文章:软考 系统架构设计师系列知识点之基于架构的软件开发方法ABSD(5) 所属章节: 第7章. 系统架构设计基础知识 第5节. 特定领域软件体系结构 相关试题 1. 基于架构的软件设计(ABSD)强调由商业、…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...
