【CS224W】(task6)Google的PageRank算法
note
- 求解pagerank:用power iteration(幂迭代)方法求解 r=M⋅r\mathbf{r}=\mathbf{M} \cdot \mathbf{r}r=M⋅r ( MMM 是重要度矩阵)
- 用random uniform teleporation解决dead-ends(自己指向自己)和spider-traps(死胡同节点)问题
文章目录
- note
- 零、内容回顾和本节概况
- 一、Graph as matrix
- 二、PageRank
- 2.1 PageRank: The “Flow” Model
- 2.2 PageRank: Matrix Formulation
- 2.3 Connection to Random Walk
- 2.3 Eigenvector Formulation
- 三、sovle PageRank: Power iteration
- 3.1 power iteration method
- 3.2 解决两大问题:random teleport
- 四、Random Walk with Restarts & Personalized PageRank
- 4.1 pagerank的变体
- 4.2 小结
- 五、代码实战:西游记人物重要度
- 附:时间安排
- Reference
零、内容回顾和本节概况
PageRank是1997年谷歌第一代搜索引擎的底层算法。大幅提高了搜索结果的相关率和质量,成为互联网第一个爆款应用,造就了传奇的谷歌公司。
PageRank是搜索引擎、信息检索、图机器学习、知识图谱、线性代数必读经典算法。
PageRank把互联网表示为由网页节点和引用链接构成的有向图,通过链接结构,计算网页节点重要度。来自重要网页节点的引用链接,权重更高。
通过线性方程组、矩阵乘法、特征值和特征向量、随机游走、马尔科夫链,五种角度,理解并求解PageRank值。讲解PageRank的收敛性分析及针对特殊节点的改进方法,最后扩展PageRank在推荐系统中计算节点相似度排序的升级变种。
- 将图视为邻接着矩阵,从线代角度理解pagerank,和前面task的随机游走和图嵌入学习。
- pagerank可用于衡量网络中节点的重要性,即如果一个节点被很多重要节点指向,则说明该节点也是重要节点;通过将图视为邻接矩阵使我们能从三个角度看待pagerank:
- flow model / 线性方程组、
- power iteration(矩阵视角)、
- web surfer随机游走
- 计算图中节点重要程度:
- PageRank
- Personalized PageRank (PPR)
- Random Walk with Restarts
- 求解PageRank:power iteration
- 在求解PageRank的过程中会遇到spider traps和dead ends的问题,可以通过random teleport解决。其中M / G 是随机游走的概率转移矩阵。
- Personalized PageRank和Random Walk with Restarts可以衡量node embedding的相似性,区别在于teleport sets。
一、Graph as matrix
我们可以通过上个task3学到的networkx进行pagerank的节点重要程度计算:
import networkx as nx
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
G = nx.star_graph(7)
# nx.draw(G, with_labels = True)
pagerank = nx.pagerank(G, alpha=0.6)
'''
{0: 0.4062486673302485,1: 0.08482161895282164,2: 0.08482161895282164,3: 0.08482161895282164,4: 0.08482161895282164,5: 0.08482161895282164,6: 0.08482161895282164,7: 0.08482161895282164}
'''
通过随机游走定义节点重要性、通过matrix factorization获得节点嵌入。
二、PageRank
- 将网页视为节点,网页之间的超链接视为边;为了简化问题,本task不考虑下面两个问题:
- Dynamic pages created on the fly2
- dark matter:不可达(如有密码等)的database generated pages
- 当今很多超链接是用于执行发布、评论、购买等行为驱动的,作为下个节点的successor;类似的栗子:论文引用,百科词条的相互引用等
- 节点重要性:in-comng links相比out-going links更不容易造假,视入边越多则节点重要性程度越高;和之前task提及的,是一个递归问题。
2.1 PageRank: The “Flow” Model
-
为节点
j定义指标rank级别:rjr_jrj,其中did_idi为节点i的出度;因为网页i的重要性是rir_iri,有did_idi个出边,所以可以定义每个节点(即每个网页)的权重为ridi\dfrac{r_i}{d_i}diri。rj=∑i→jridir_j=\sum_{i \rightarrow j} \frac{r_i}{d_i} rj=i→j∑diri -
这里节点的权重其实就是对所有加权求和过的入边,累加计算。栗子:1839年的web,其中的 flow等式为ry=ry/2+ra/2ra=ry/2+rmrm=ra/2\begin{aligned} & r_y=r_y / 2+r_a / 2 \\ & r_a=r_y / 2+r_m \\ & r_m=r_a / 2 \end{aligned} ry=ry/2+ra/2ra=ry/2+rmrm=ra/2

2.2 PageRank: Matrix Formulation
PageRank的矩阵形式。
- 随机邻接矩阵stochastic adjacency matrix M:
- did_idi:节点iii的出度;
- 如果节点iii指向节点jjj则M矩阵的对应元素值:Mji=1diM_{j i}=\frac{1}{d_i}Mji=di1;显然M矩阵中每列的元素累加和为1(因为当前列时平均加权元素)。
- flow equations:r=M⋅r\boldsymbol{r}=M \cdot \boldsymbol{r} r=M⋅r
- 上面公式中,等式右边的rrr是rank vector,衡量网页的重要性程度。

flow等式和矩阵形式:

2.3 Connection to Random Walk
和随机游走联系。
- 当从一个web网页节点中进行随机游走,ttt时间是在网页iii上,t+1t+1t+1时刻从iii节点的出边中随机抽取一条边走动;
- 平稳分布stationary distribution等式:p(t+1)=M⋅p(t)=p(t)p(t+1)=M \cdot p(t)=p(t) p(t+1)=M⋅p(t)=p(t)其中M是转移概率矩阵,如果达到上面式子这种状态,则p(t)p(t)p(t)是随机游走的平稳分布向量。
2.3 Eigenvector Formulation
特征向量形式。
- 在之前的task中提到的无向图,直接使用邻接矩阵λc=Ac\lambda c=A cλc=Ac,求出该矩阵的特征向量eigenvector,即节点特征,如上个task我们对地铁路线求解每个节点的
nx.degree_centrality(G)然后可视化。 - PageRank的随机邻接矩阵stochastic adjacency matrix M,flow equation也有类似的特征向量等式(如下),此时的rrr即M的图的平稳分布的一个随机游走:1⋅r=M⋅r1 \cdot r=M \cdot r 1⋅r=M⋅r

结论:可通过Power iteration高效求解rrr。
三、sovle PageRank: Power iteration
3.1 power iteration method
方法:power iteration method 幂迭代法求解pagerank
- 初始赋值:r(0)=[1/N,…,1/N]T\boldsymbol{r}^{(0)}=[1 / N, \ldots, 1 / N]^Tr(0)=[1/N,…,1/N]T
- 迭代r(t+1)=M⋅r(t)\boldsymbol{r}^{(\boldsymbol{t}+\mathbf{1})}=\boldsymbol{M} \cdot \boldsymbol{r}^{(t)}r(t+1)=M⋅r(t),计算每个节点的pagerank,直到收敛到(∑i∣rit+1−rit∣<ϵ)\left(\sum_i\left|r_i^{t+1}-r_i^t\right|<\epsilon\right)(∑irit+1−rit<ϵ),其中did_idi为节点iii的出度;迭代式为:rj(t+1)=∑i→jri(t)dir_j^{(t+1)}=\sum_{i \rightarrow j} \frac{r_i^{(t)}}{d_i} rj(t+1)=i→j∑diri(t)
- 迭代停止条件:∣r(t+1)−r(t)∣1<ε\left|\boldsymbol{r}^{(\boldsymbol{t}+1)}-\boldsymbol{r}^{(t)}\right|_1<\varepsilonr(t+1)−r(t)1<ε,这里是范数L1,当然也可以使用其他vector norm方法(如Euclidean等)。
- 栗子:

3.2 解决两大问题:random teleport
- 两大问题:
- spider trap:所有出边都在一个节点组内,会吸收所有重要性,随机游走在圈子中。
- dead end:没有出边,造成重要性泄露
- 解决方法:random jumps or teleports
- random surfer每一步以概率 β\betaβ 随机选择一条链接(M), 以概率 1−β1-\beta1−β 随机跳到一个网页 上。
整体公式为: rj=∑i→jβridi+(1−β)1N(dir_j=\sum_{i \rightarrow j} \beta \frac{r_i}{d_i}+(1-\beta) \frac{1}{N} \quad\left(d_i\right.rj=∑i→jβdiri+(1−β)N1(di 是节点 i\mathrm{i}i 的出度)
- random surfer每一步以概率 β\betaβ 随机选择一条链接(M), 以概率 1−β1-\beta1−β 随机跳到一个网页 上。
- random jumps or teleports栗子举例:
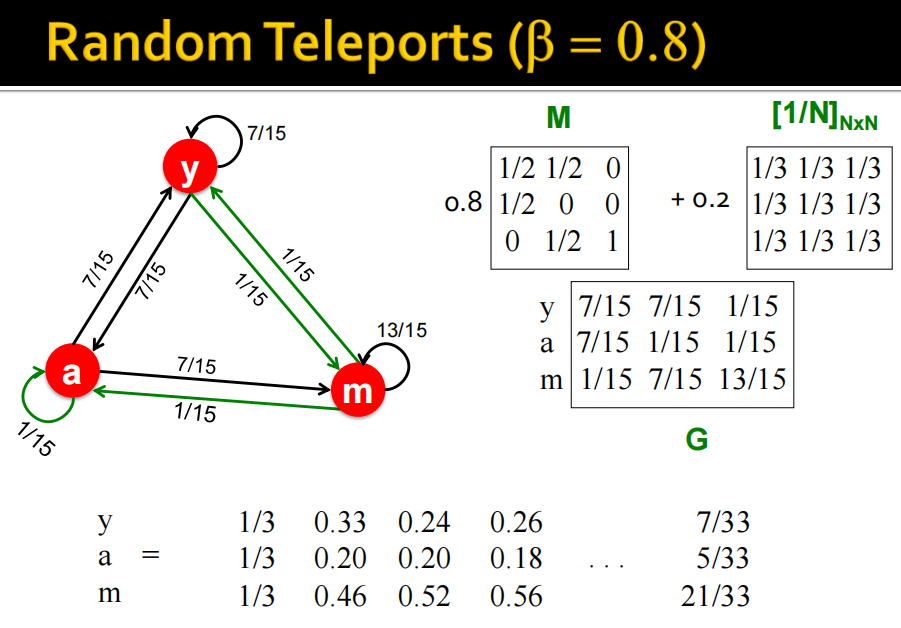
pagerank结果栗子:

四、Random Walk with Restarts & Personalized PageRank
4.1 pagerank的变体

4.2 小结

五、代码实战:西游记人物重要度
# !/usr/bin/python
# -*- coding: utf-8 -*-
import networkx as nx # 图数据挖掘
import numpy as np # 数据分析
import random # 随机数
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
plt.rcParams['font.sans-serif']=['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False # 用来正常显示负号
# OpenKG-四大名著人物关系知识图谱和OWL本体:http://www.openkg.cn/dataset/ch4masterpieces# (一)读取数据和可视化任务关系
# 导入 csv 文件定义的有向图
df = pd.read_csv('data/三国演义/triples.csv')
edges = [edge for edge in zip(df['head'], df['tail'])]
G = nx.DiGraph()
G.add_edges_from(edges) # 添加有向边# 可视化
plt.figure(figsize=(15,14))
pos = nx.spring_layout(G, iterations=3, seed=5)
# nx.draw(G, pos, with_labels=True)
nx.draw_networkx(G, pos, with_labels = True)
plt.show()
可以看到人物关系图如下,边是有向边,如head为关羽,tail为刘备是,relation是younger_sworn_brother,label是义弟。

# (二)计算每个节点的pagerank重要度
pagerank = nx.pagerank(G, # NetworkX graph 有向图,如果是无向图则自动转为双向有向图alpha=0.85, # Damping Factorpersonalization=None, # 是否开启Personalized PageRank,随机传送至指定节点集合的概率更高或更低max_iter=100, # 最大迭代次数tol=1e-06, # 判定收敛的误差nstart=None, # 每个节点初始PageRank值dangling=None, # Dead End死胡同节点)# 按pagerank重要度进行排序
sorted(pagerank.items(),key=lambda x : x[1], reverse=True)# (三)设置节点和连接的参数
# 用节点尺寸可视化PageRank值
# 节点尺寸
node_sizes = (np.array(list(pagerank.values())) * 8000).astype(int)
# 节点颜色
M = G.number_of_edges()
edge_colors = range(2, M + 2)
# 绘图
plt.figure(figsize=(15,14))# 绘制节点
nodes = nx.draw_networkx_nodes(G, pos, node_size=node_sizes, node_color=node_sizes)# 绘制连接
edges = nx.draw_networkx_edges(G,pos,node_size=node_sizes, # 节点尺寸arrowstyle="->", # 箭头样式arrowsize=20, # 箭头尺寸edge_color=edge_colors, # 连接颜色edge_cmap=plt.cm.plasma,# 连接配色方案,可选:plt.cm.Blueswidth=4 # 连接线宽
)# 设置每个连接的透明度
edge_alphas = [(5 + i) / (M + 4) for i in range(M)]
for i in range(M):edges[i].set_alpha(edge_alphas[i])# (四)图例
# pc = mpl.collections.PatchCollection(edges, cmap=cmap)
# pc.set_array(edge_colors)
# plt.colorbar(pc)ax = plt.gca()
ax.set_axis_off()
plt.show()
比如左下角的又大又黄又亮的节点就是诸葛亮,灰常重要。

附:时间安排
| 任务 | 任务内容 | 截止时间 | 注意事项 |
|---|---|---|---|
| 2月11日开始 | |||
| task1 | 图机器学习导论 | 2月14日周二 | 完成 |
| task2 | 图的表示和特征工程 | 2月15、16日周四 | 完成 |
| task3 | NetworkX工具包实践 | 2月17、18日周六 | 完成 |
| task4 | 图嵌入表示 | 2月19、20日周一 | 完成 |
| task5 | deepwalk、Node2vec论文精读 | 2月21、22、23、24日周五 | 完成 |
| task6 | PageRank | 2月25、26日周日 | 完成 |
| task7 | 标签传播与节点分类 | 2月27、28日周二 | |
| task8 | 图神经网络基础 | 3月1、2日周四 | |
| task9 | 图神经网络的表示能力 | 3月3日周五 | |
| task10 | 图卷积神经网络GCN | 3月4日周六 | |
| task11 | 图神经网络GraphSAGE | 3月5日周七 | |
| task12 | 图神经网络GAT | 3月6日周一 |
Reference
[1] Pagerank-算法讲解:https://www.bilibili.com/video/BV1uP411K7yN
[2] PageRank代码实战-西游记人物重要度:https://www.bilibili.com/video/BV1Wg411H7Ep
[3] cs224w(图机器学习)2021冬季课程学习笔记4 Link Analysis: PageRank (Graph as Matrix)
[4] CS224W官网:https://web.stanford.edu/class/cs224w/index.html
[5] CS224W-11 成就了谷歌的PageRank
[6] 锋哥笔记-pagerank
[7] 百科-L1范数正则化
[8] https://github.com/TommyZihao/zihao_course/tree/main/CS224W
[9] 【经典论文阅读】PageRank原理与实践
[10] Page L, Brin S, Motwani R, et al. The PageRank citation ranking: Bringing order to the web[R]. Stanford InfoLab, 1999.
相关文章:

【CS224W】(task6)Google的PageRank算法
note 求解pagerank:用power iteration(幂迭代)方法求解 rM⋅r\mathbf{r}\mathbf{M} \cdot \mathbf{r}rM⋅r ( MMM 是重要度矩阵)用random uniform teleporation解决dead-ends(自己指向自己)和spider-traps(…...

Python安装拓展库及常用的pip命令及其用法
Python安装拓展库 在Python中,库是一些预先编写好的代码和函数,它们可以帮助你解决特定的问题。如果你想要扩展Python库,通常有两种方法:使用现有的第三方库,或者编写自己的库。 1.使用现有的第三方库 Python社区中…...

这9道软件测试面试题,就能刷掉90%的软件测试员
转眼就要到“金三银四”了,没点真本事真技术,没点面试经验,不了解点职场套路,如何过五关斩六将?如何打败面试官?如何拿下那梦寐以求的offer? 如果你的跳槽意向已经很确定,那么请往下…...
【大数据】大数据Hadoop生态圈
文章目录大数据Hadoop生态圈-组件介绍1、HDFS(分布式文件系统)2、MapReduce(分布式计算框架)3、Spark(分布式计算框架)4、Flink(分布式计算框架)5、Yarn/Mesos(分布式资源…...
python读取tif图像+经纬度
python读取tif的包很多,但大都只能读出图像像素值,不能读取到经纬度信息。原因:TIFF 简单理解就是一种图像格式,类似于 jpg、png 等。GeoTIFF 就是在普通 TIFF 文件上增加了地理位置、投影信息、坐标信息等,常用于遥感…...
Kali安装配置vulhub
一、vulhubVulhub是一个基于docker和docker-compose的漏洞环境集合,进入对应目录并执行一条语句即可启动一个全新的漏洞环境,主要利用于漏洞复现。Vulhub的官方地址为www.vulhub.org。二、搭建vulhub靶场2.1 开启kali虚拟机2.2 安装docker先更新一下软件…...

【进击的算法】动态规划——不同维度的背包问题
文章目录前言动态规划的维度二维动规leetcode416、分割等和子集leetcode1049. 最后一块石头的重量 IIleetcode494、目标和三维动规leetcode474. 一和零结语前言 大家好久不见,这次我们一起来学习一下动态规划中怎么确定维度,和对应问题如何解决。 动态…...
udiMagic 导入 Excel to Tally ERP Crack
关于 udiMagic 软件 udiMagic 是一款可帮助您快速轻松地将数据导入 Tally ERP 的应用程序。它由 Shweta Softwares 创建和分发,于2007 年首次推出。 您可以在 USB 闪存驱动器 [旅行许可证] 中携带 udiMagic,并在具有任何 Tally 版本的任何计算机上使用…...

Redis实现分页和多条件模糊查询方案
导言 Redis是一个高效的内存数据库,它支持包括String、List、Set、SortedSet和Hash等数据类型的存储,在Redis中通常根据数据的key查询其value值,Redis没有模糊条件查询,在面对一些需要分页、排序以及条件查询的场景时(如评论&…...

【H5 | CSS | JS】如何实现网页打字机效果?快收下这份超详细指南(附源码)
💂作者简介: THUNDER王,一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学会计学专业大二本科在读,同时任汉硕云(广东)科技有限公司ABAP开发顾问。在学习工作中,我通常使用偏后…...

Airbyte,数据集成的未来
Gartner 曾预计,到 2025 年,80% 寻求扩展数字业务的组织将失败。因为他们没有采用现代方法来进行数据和分析治理。数据生态是基础架构生态的最重要一环,数据的处理分发与计算,从始至终贯穿了整个数据流通生态。自从数据集中在数据…...

00.内容安排
内容安排如下01.Linux基本命令0.2 vim编辑器,gcc、gdb、makefile、动/静态库制作使用03.文件 I/O 常用函数、文件读写原理、进程控制快概念、阻塞、非阻塞概念04.文件常用操作函数、目录常用操作函数、重定向05.进程控制fork、exec函数组、进程回收 wait/waitpid06.…...
FreeRTOS任务基础知识
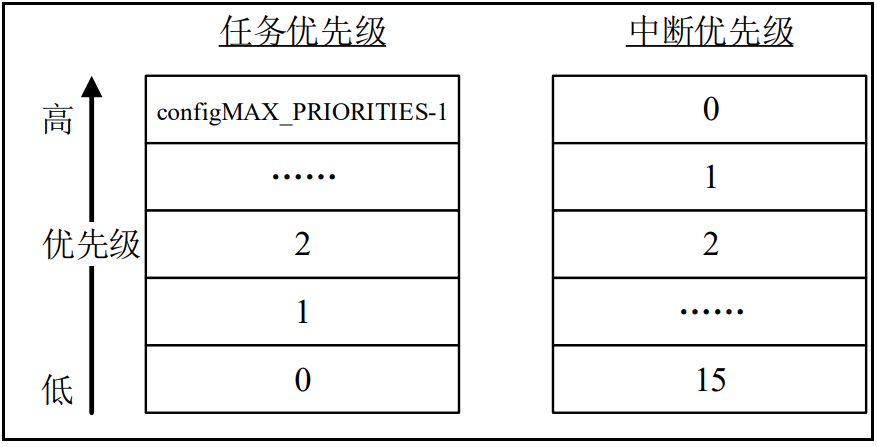
单任务和多任务系统单任务系统单任务系统的编程方式,即裸机的编程方式,这种编程方式的框架一般都是在main()函数中使用一个大循环,在循环中顺序的执行相应的函数以处理相应的事务,这个大循环的部分可以视为…...
JDBC-API详解、SQL注入演示、连接池
文章目录JDBC1,JDBC概述1.1 JDBC概念1.2 JDBC本质1.3 JDBC好处2,JDBC快速入门2.1 编写代码步骤2.2 具体操作3,JDBC API详解3.1 DriverManager3.2 Connection (事务归我管)3.2.1 获取执行对象3.2.2 事务管理3.3 Stateme…...
)
C 学习笔记 —— 动态分配内存(malloc)
文章目录分配内存malloccallocrealloc创建数组方式free的重要性举例常见动态分配内存错误忘记检查所请求的内存对NULL指针进行解引用对分配的内存越界访问释放一块内存后,继续使用释放一块内存的一部分是不允许的内存泄漏分配内存 当一个数组声明时,需要…...

RK3588通用布线设计指南
(1)走线长度应包含过孔和封装。(2)由于表贴器件的焊盘会导致阻抗降低,为减小阻抗突变的影响,建议在表贴焊盘的正下方按焊盘大小挖去一层参考层。常用的表贴器件有:电容、 ESD、共模抑制电感、连…...

ChatGPT也懂如何设计开发板!?
到底应该如何设计一款开发板?我们问了一下最近风很大的ChatGPT,得出了这样的回答: 或者这样的回答: 显而易见,RK3568开发板是一款功能丰富,性能优异,易于开发的高性能开发板,适用于各…...
去了字节跳动,才知道年薪40W的测试居然有这么多?
今年大环境不好,内卷的厉害,薪资待遇好的工作机会更是难得。最近脉脉职言区有一条讨论火了: 哪家互联网公司薪资最‘厉害’? 下面的评论多为字节跳动,还炸出了很多年薪40W的测试工程师 我只想问一句,现在的…...

2023前端面试知识点总结
原型 JavaScript中的对象都有一个特殊的 prototype 内置属性,其实就是对其他对象的引用 几乎所有的对象在创建时 prototype 属性都会被赋予一个非空的值,我们可以把这个属性当作一个备用的仓库 当试图引用对象的属性时会出发get操作,第一步时…...
FL StudioV21电脑版水果编曲音乐编辑软件
这是一款功能十分丰富和强大的音乐编辑软件,能够帮助用户进行编曲、剪辑、录音、混音等操作,让用户能够全面地调整音频。FL水果最新版是一款专业级别的音乐编曲软件,集合更多的编曲功能为一身,可以进行录音、编辑、制作、混音、调…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
