【算法】最短路算法
😀大家好,我是白晨,一个不是很能熬夜😫,但是也想日更的人✈。如果喜欢这篇文章,点个赞👍,关注一下👀白晨吧!你的支持就是我最大的动力!💪💪💪

文章目录
- 📗前言
- 📘最短路算法
- 🎗️Dijkstra
- 🍕朴素Dijkstra算法
- 🍔堆优化Dijkstra算法
- 🎞️Bellman-Ford
- 🍟有边数限制的最短路
- 🎟️SPFA
- 🌭SPFA求最短路
- 🍿SPFA判断负环
- 🎫Floyd
- 🧂Floyd求最短路
- 📙后记
📗前言
咕咕咕,我是🕊白晨,最近一直在忙开学考试,托更了很久,果咩纳塞😱。

这次为大家分享的是图论中的最短路算法。考虑到最短路算法的复杂性以及本文新手向的教程,本次算法讲解列举了大量例子并且配上了大量动图。本篇文章所有的代码实现都是算法向的,以快速实现和效率为主,如果出现算法向的代码实在看不懂,可以参考白晨的工程向实现的代码,工程向代码链接:Graph。
📘最短路算法
最短路算法是指 一个图中,求某一个节点到其他节点的最短路径(最小权值路径)的算法。
最短路算法是图论中一类很重要的算法,也是算法题中经常会使用的一类算法。这种算法也可以和实际问题结合起来,比如 你要从西安到上海,要找到用时最短的一条路径,就需要这种算法。
🎗️Dijkstra
🍕朴素Dijkstra算法
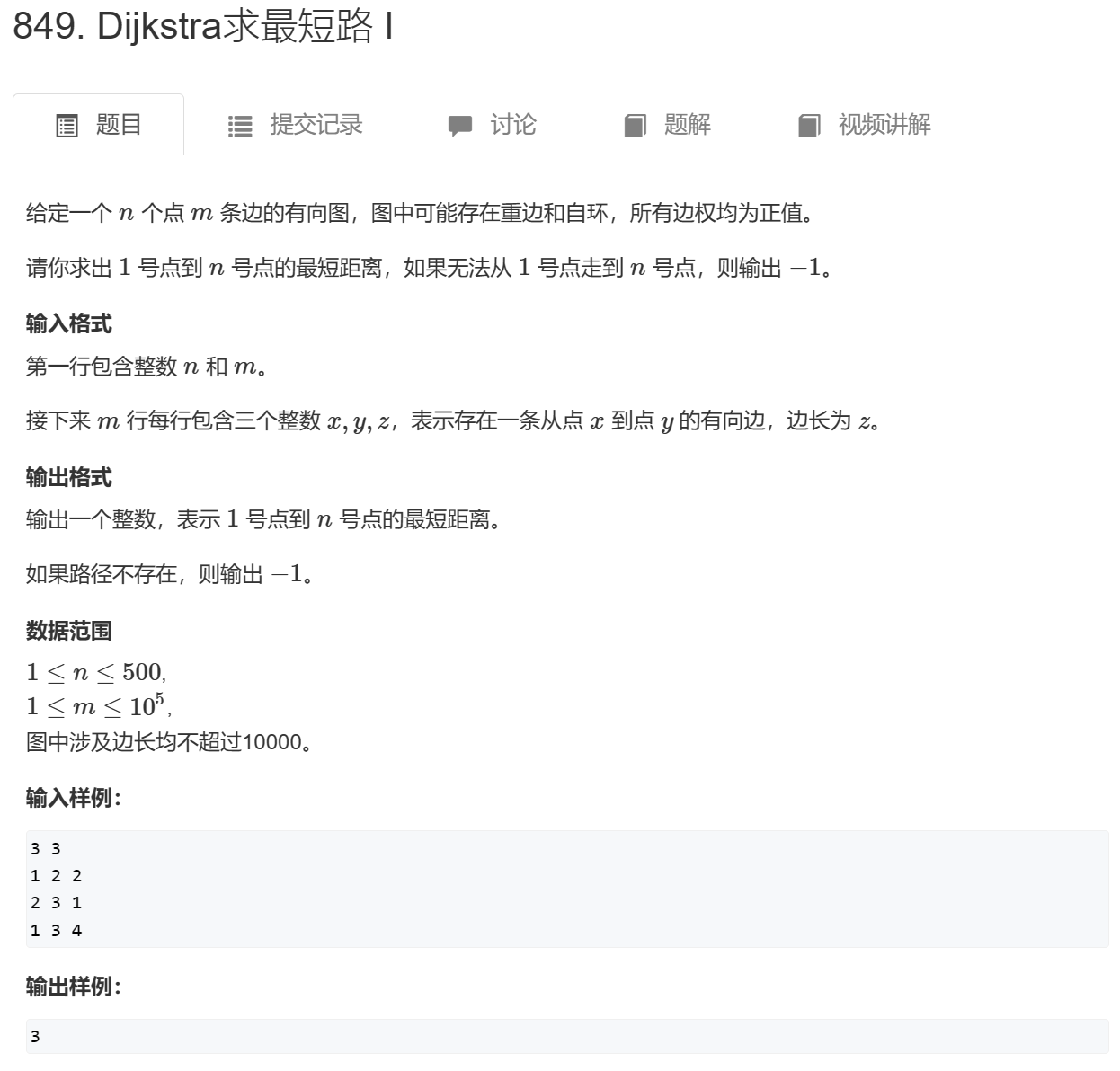
🍬原题链接:Dijkstra求最短路 I
🪅算法思想:
朴素Dijkstra算法为单源最短路算法,适合稠密图,时间复杂度为 O(n2)O(n^2)O(n2) (n为节点个数),对于边的存储结构为
邻接矩阵。
注意:Dijkstra算法必须要保证所有边的权值为正,否则算法的贪心策略证明失效。
- 具体做法
- 初始化
dist数组(初始化为无限大) 以及 dist[1]=0dist[1] = 0dist[1]=0(一号节点到自己的距离为0)。 - 遍历
dist数组,选出其中距离最短的节点,选中此节点加入已确定最短距离的节点的集合S。 - 根据上面确定节点的最短距离 更新 到达其他节点的最短距离(
S集合中节点距离不可能再被更新)。 - 重复2、3过程 N 次,N次迭代后,全部点的最短距离已经被确定。
以上的思想本质上来说是一种贪心策略,为什么能保证每次选中的距离1号节点最近的节点的路径就是最短路径呢?
Dijsktra迪杰斯特拉算法的证明(数学归纳法)和代码实现
证明见上面文章。
现在,我们来模拟一下Dijkstra算法的具体流程:

动画演示如下:

🪆代码实现:
// 朴素Dijkstra算法
#include <iostream>
#include <cstring>using namespace std;const int N = 510, INF = 0x3f3f3f3f;int n, m;int g[N][N]; // 邻接矩阵
int dist[N]; // 存储最短距离
bool book[N]; // 是否已确定最短路int Dijkstra()
{memset(dist, 0x3f, sizeof(dist));dist[1] = 0;// 循环n次for (int i = 0; i < n; ++i){// 选出距离1号节点距离最短的节点int u = -1;for (int j = 1; j <= n; ++j)if (!book[j] && (u == -1 || dist[u] > dist[j])) u = j;book[u] = true;// 更新边for (int i = 1; i <= n; ++i)if (!book[i] && dist[u] + g[u][i] < dist[i]) dist[i] = dist[u] + g[u][i];}if (dist[n] == INF) return -1;else return dist[n];
}int main()
{scanf("%d%d", &n, &m);memset(g, 0x3f, sizeof(g));while (m--){int a, b, w;scanf("%d%d%d", &a, &b, &w);g[a][b] = min(g[a][b], w); // 重边保留最小的边}printf("%d", Dijkstra());return 0;
}
🍔堆优化Dijkstra算法

🍬原题链接:Dijkstra求最短路 II
🪅算法思想:
堆优化Dijkstra算法为单源最短路算法,适用于稀疏图,时间复杂度为 O(mlogn)O(mlogn)O(mlogn)(m为边数,n为节点数),边的存储结构为
邻接表。
相比于朴素版,本算法对于寻找路径最短的节点的过程进行了优化,改为了用小根堆堆存储最短路径,根据小根堆的特性,最短的路径就是堆顶元素,这样就省去了寻找最短路径的过程。
注意:Dijkstra算法必须要保证所有边的权值为正,否则算法的贪心策略证明失效。
- 具体做法
- 初始化
dist数组,dist[1]=0dist[1] = 0dist[1]=0,将{0,1}(距离为0,节点序号为1)入堆。 - 出堆顶元素,根据新确定最短路径以及节点下标更新其他路径(本次选用的存储结构为邻接表,所以直接遍历每个节点对应的链表即可)。
- 重复2过程,直到堆为空。
- 初始化
🪆代码实现:
// 堆优化Dijkstra算法
#include <iostream>
#include <queue>
#include <cstring>using namespace std;typedef pair<int, int> PII;const int N = 150010, INF = 0x3f3f3f3f;int n, m;// 这里只是我习惯的邻接表存储方式,也可以用结构体存储,只要能遍历一个节点的所有出边就可以
int g[N], e[N], ne[N], val[N], idx;// g为邻接表,e,ne,val为单链表,e存放节点序号,ne存放子节点下标,val存储权值
bool book[N]; // 此节点是否已经确定最短路径
int dist[N]; // 存储到1号节点的最短路径大小// 加边
void add(int a, int b, int w)
{e[idx] = b, val[idx] = w, ne[idx] = g[a], g[a] = idx++;
}int Dijkstra()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;priority_queue<PII, vector<PII>, greater<PII>> pq; // 小根堆pq.push({0, 1}); // 前面为距离,后面为节点序号while (pq.size()){auto t = pq.top();pq.pop();int st = t.first, node = t.second;// 由于题目有重边,所以可能会把一个节点更新多次,由于小根堆是距离小的先出,所以小边会先出确定最短路径,后面出的直接忽略即可if (book[node]) continue; book[node] = true;for (int i = g[node]; i != -1; i = ne[i]){int j = e[i];if (dist[node] + val[i] < dist[j]){dist[j] = dist[node] + val[i];pq.push({dist[j], j});}}}if (dist[n] == INF) return -1;else return dist[n];
}int main()
{scanf("%d%d", &n, &m);memset(g, -1, sizeof g);while (m--){int a, b, w;scanf("%d%d%d", &a, &b, &w);add(a, b, w);}printf("%d", Dijkstra());return 0;
}
🎞️Bellman-Ford

上图要求0点到其余点的最短距离,用Dijkstra算法可以吗?

可以看到Dijkstra这种贪心算法是完全失效了,第一次加入S集合的节点本来距离就应该确定了,但是有负权边时,会被继续更新。有负权边时,就应该把任务交给下面要介绍的Bellman-Ford算法了。
🍟有边数限制的最短路
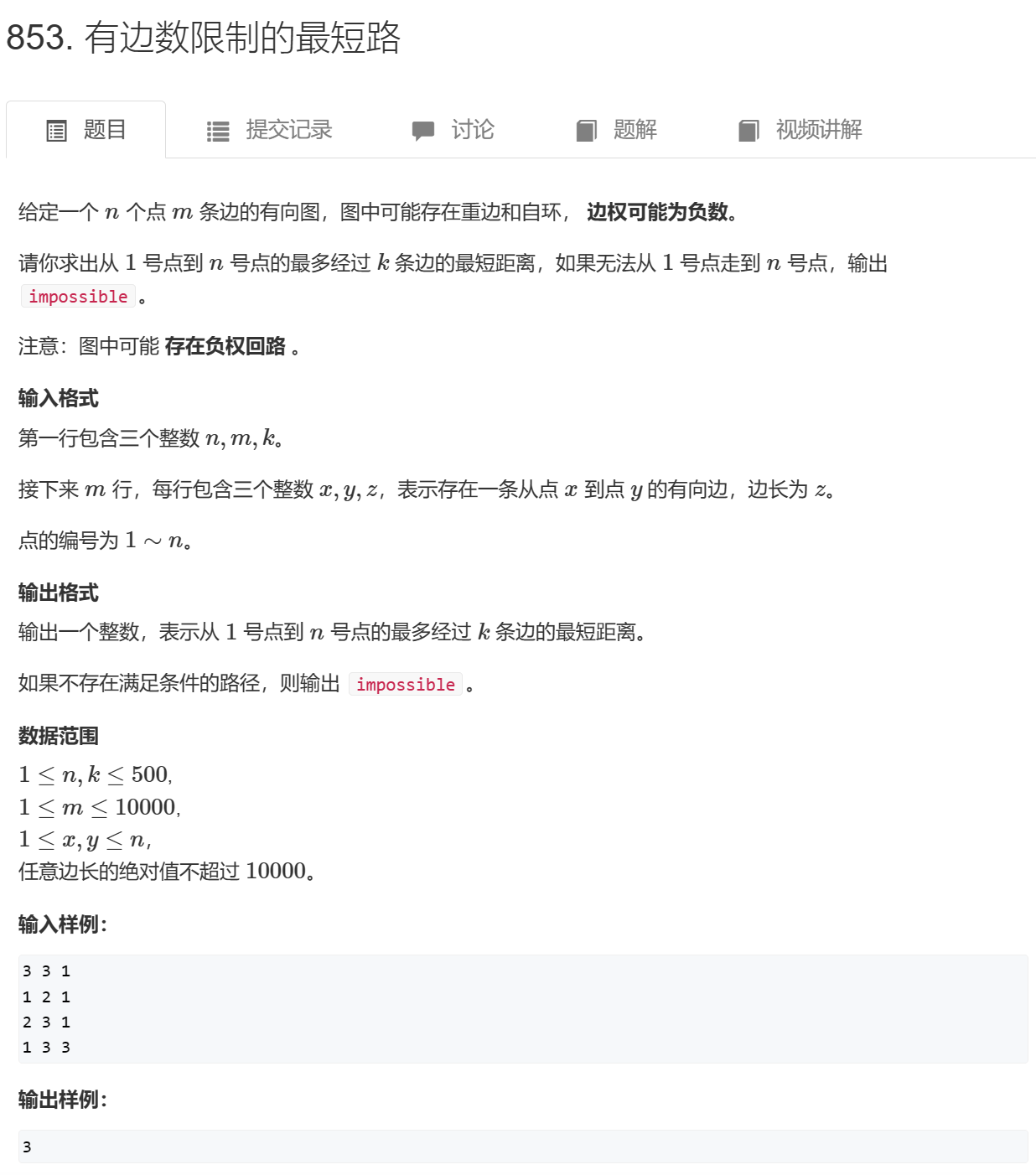
🍬原题链接:有边数限制的最短路
🪅算法思想:
Bellman-Ford算法,带负权边单源最短路算法,时间复杂度为 O(nm)O(nm)O(nm)(顶点数*边数),本质上就是一个无脑遍历边的算法,所以边的存储不做要求,只要能遍历到全部边就可以,可以用结构体,也可以用邻接表等。
注意:Bellman-Ford算法可以求带负权边的最短路径,但是如果一个图中有负权回路,最短路径则不一定存在。

上图中,2、3、4号节点形成了一个环,如果要求1号节点到5号节点距离的最小值,可以走 1-2-3-4-3-5,总权值为3,也可以走 1-2-3-4-3-4-2-3-5,总权值为2。以此类推,可以无限走这个环,在没有路径边数的限制下,最小值为负无穷。
所以,Bellman-Ford算法可以用来求从 起始点 到 终点 的最多经过 k条边的最短距离,也可以用来判断负环(一般用SPFA算法判断,不用这个算法)。
- 具体做法:循环k次,每次遍历全部的边, 按照
dist[b] = min(dist[b], dist[a] + w)更新b点到1号节点的距离即可。
与Dijkstra算法演示的例子相同:

对应的Bellman-Ford算法的动画演示如下:

🪆代码实现:
#include <iostream>
#include <cstring>using namespace std;const int N = 510, M = 10010, INF = 0x3f3f3f3f;struct Edge
{int a, b, w;
}edges[M];int n, m, k;
int dist[N], bkup[N]; // bkup是dist的备份,每次必须使用备份遍历,否则会出现更新顺序影响结果的情况void bellman_ford()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;for (int i = 0; i < k; ++i){// 每次必须用上一次更新完的值进行更新,如果直接用dist数组进行更新,会出现// 如果有3->1,2->3这两条边,k为1,如果先遍历到3->1这条边,dist[3]被更新,下面遍历2->3这条边,dist[2]也会被更新// 但是2节点到1节点必须要走两条边,不满足题意,所以每次必须用上一次更新完的值进行更新memcpy(bkup, dist, sizeof dist);for (int j = 0; j < m; ++j){auto& e = edges[j];dist[e.b] = min(dist[e.b], bkup[e.a] + e.w);}}
}int main()
{scanf("%d%d%d", &n, &m, &k);for (int i = 0; i < m; ++i){int a, b, w;scanf("%d%d%d", &a, &b, &w);edges[i] = {a, b, w};}bellman_ford();if (dist[n] > INF / 2) printf("impossible"); // 这里要注意,由于有负权边dist[a] = INF , dist[b] = INF, a->b w = -1时,dist[b] = INF - 1,小于INF,所以这里判断是否在一个区间else printf("%d", dist[n]);return 0;
}
🎟️SPFA
下面来看一个例子:

上面这个图,如果按照Bellman-Ford算法做,每次循环只有一次更新是有效的,其余全都是无效循环,大大浪费了时间。

我们发现,只有上一轮被更新过的节点,这一轮才会以该节点为出发点继续更新,所以能不能存储上一轮更新过的节点,这一轮直接遍历这些节点的出边,不就能大大减少无效的循环了吗?
🌭SPFA求最短路

🍬原题链接:SPFA求最短路
🪅算法思想:
SPFA算法,带负权单源最短路算法,时间复杂度一般为O(m)O(m)O(m),最坏为O(nm)O(nm)O(nm),本算法优化了Bellman-Ford算法每次遍历全部边的过程,本质上是
BFS,边的存储结构为邻接矩阵。
-
核心思路:只有 dist[a] 更新了, a->b 边才会被使用,否则不会使用a->b这条边,所以本算法存储更新过的最短路,很像Dijkstra堆优化版本。
-
具体做法:
- 初始化
dist数组,dist[1]=0dist[1] = 0dist[1]=0,将1号节点其入队。 - 广度优先搜索,出队节点元素,遍历每个节点的出边,更新,直到队列为空。
- 初始化
SPFA算法动画演示:

🪆代码实现:
// SPFA
#include <iostream>
#include <queue>
#include <cstring>using namespace std;const int N = 100010, INF = 0x3f3f3f3f;int n, m;
int g[N], e[N], ne[N], val[N], idx;
int dist[N];
bool book[N]; // 标记是否在队列中int SPFA()
{memset(dist, 0x3f, sizeof dist);dist[1] = 0;queue<int> q;q.push(1);book[1] = true;while (q.size()){int u = q.front();q.pop();// 出队列以后记得更新状态book[u] = false;for (int i = g[u]; i != -1; i = ne[i]){int j = e[i];if (dist[u] + val[i] < dist[j]){dist[j] = dist[u] + val[i];// 防止重复添加if (!book[j]){q.push(j);book[j] = true;}}}}return dist[n];
}void add(int a, int b, int w)
{e[idx] = b, val[idx] = w, ne[idx] = g[a], g[a] = idx++;
}int main()
{scanf("%d%d", &n, &m);memset(g, -1, sizeof g); // g必须在add函数前更新for (int i = 0; i < m; ++i){int a, b ,w;scanf("%d%d%d", &a, &b, &w);add(a, b, w);}int ret = SPFA();if (ret == INF) puts("impossible");else printf("%d\n", ret);return 0;
}
🍿SPFA判断负环

🍬原题链接:spfa判断负环
🪅算法思想:
- 核心思想:设置一个cnt数组用来存储1号点到其他点路径中边的数量,使用SPFA算法进行更新,如果到一个节点到1号节点路径中边的数量 cnt[i]>=ncnt[i] >= ncnt[i]>=n,说明路径中出现环,如果出现环,一定是负环,因为正环不会 dist[i]+环的路径<=dist[i]dist[i] + 环的路径 <= dist[i]dist[i]+环的路径<=dist[i] 也就不会被更新。
如何证明cnt[i]>=ncnt[i] >= ncnt[i]>=n就一定出现环呢?
反证法,如果cnt[i]>=ncnt[i] >= ncnt[i]>=n没有环,说明从1到 i 没有走过任何一个重复的节点,但是一共只有n个节点,当有n条边时,连接了n+1个节点,根据抽屉原理,必定有相同的节点,所以必定有环。
🪆代码实现:
// SPFA
#include <iostream>
#include <queue>
#include <cstring>using namespace std;const int N = 100010, INF = 0x3f3f3f3f;int n, m;
int g[N], e[N], ne[N], val[N], idx;
int dist[N], cnt[N];
bool book[N];bool SPFA()
{// 由于本题目只是用来判断负环,dist数组不表示最短距离,可以不需要初始化,这样更新的就只有负权边了queue<int> q;// 将全部节点入队,这里没有说是连通图,所以必须全部点先入队列for (int i = 1; i <= n; ++i){q.push(i);book[i] = true;}while (q.size()){int u = q.front();q.pop();// 出队列以后记得更新状态book[u] = false;for (int i = g[u]; i != -1; i = ne[i]){int j = e[i];if (dist[u] + val[i] < dist[j]){dist[j] = dist[u] + val[i];cnt[j] = cnt[u] + 1; // 路径更新if (cnt[j] >= n) return true;// 防止重复添加if (!book[j]){q.push(j);book[j] = true;}}}}return false;
}void add(int a, int b, int w)
{e[idx] = b, val[idx] = w, ne[idx] = g[a], g[a] = idx++;
}int main()
{scanf("%d%d", &n, &m);memset(g, -1, sizeof g); // g必须在add函数前更新for (int i = 0; i < m; ++i){int a, b ,w;scanf("%d%d%d", &a, &b, &w);add(a, b, w);}if (SPFA()) puts("Yes");else puts("No");return 0;
}
🎫Floyd
🧂Floyd求最短路

🍬原题链接:Floyd求最短路
🪅算法思想:
Floyd算法,
多源最短路算法(一次可以求出所有节点到其他节点的最短路,有无负权边皆可使用),时间复杂度为O(n3)O(n^3)O(n3),本质上是区间动态规划,核心代码只有四行,非常牛。边的存储结构:邻接矩阵。
-
状态:f[i,j,k]f[i, j, k]f[i,j,k]表示从iii走到jjj的路径上除了iii和jjj以外 只经过1∼k1\sim k1∼k号节点 的所有路径的最短距离。eg.f[5,6,3]f[5, 6, 3]f[5,6,3]表示 从555号节点走到666号节点 只经过 1,2,31,2,31,2,3 这三个节点的最短距离
-
最初状态:f[i,j,k]=∞f[i, j, k] = \inftyf[i,j,k]=∞
-
状态转移方程:f[i,j,k]=min(f[i,j,k],f[i,k,k−1]+f[k,j,k−1])f[i, j, k] = min(f[i, j, k], f[i, k, k - 1] + f[k, j, k -1])f[i,j,k]=min(f[i,j,k],f[i,k,k−1]+f[k,j,k−1]),iii节点到jjj节点只经过1∼k1\sim k1∼k号节点的最短距离等于 本身原值 和 iii节点到kkk节点只经过1∼k−11 \sim k-11∼k−1号节点最短距离和kkk节点到j节点只经过1∼k−11\sim k-11∼k−1号节点最短距离之和的最小值。
由于状态转移中,k层状态只需要用到k-1层状态,所以k这一维可以被优化掉。
🪆代码实现:
// Floyd算法
#include <iostream>
#include <cstring>using namespace std;const int N = 210, INF = 0x3f3f3f3f;int n, m, q;int g[N][N];void Floyd()
{// 在计算第k层的f[i, j]的时候必须先将第k - 1层的所有状态计算出来,所以需要把k放在最外层for (int k = 1; k <= n; ++k)for (int i = 1; i <= n; ++i)for (int j = 1; j <= n; ++j)g[i][j] = min(g[i][j], g[i][k] + g[k][j]);
}int main()
{scanf("%d%d%d", &n, &m, &q);for (int i = 1; i <= n; ++i)for (int j = 1; j <= n; ++j)if (i == j) g[i][j] = 0;else g[i][j] = INF;while (m--){int a, b, w;scanf("%d%d%d", &a, &b, &w);g[a][b] = min(g[a][b], w);}Floyd();while (q--){int a, b;scanf("%d%d", &a, &b);if (g[a][b] > INF / 2) puts("impossible");else printf("%d\n", g[a][b]);}return 0;
}
📙后记
最后总结一下上面所有算法:
- 单源最短路算法
- 朴素Dijkstra:贪心算法,必须保证无负权边,适合
稠密图,时间复杂度为 O(n2)O(n^2)O(n2) (n为节点个数),对于边的存储结构为邻接矩阵。 - 堆优化Dijkstra:贪心算法,必须保证无负权边,适用于
稀疏图,时间复杂度为 O(mlogn)O(mlogn)O(mlogn)(m为边数,n为节点数),边的存储结构为邻接表。 - Bellman-Ford:循环遍历,时间复杂度为 O(nm)O(nm)O(nm)(顶点数*边数),所以
边的存储不做要求,只要能遍历到全部边就可以,可以用结构体,也可以用邻接表等。 - SPFA:BFS,时间复杂度一般为O(m)O(m)O(m),最坏为O(nm)O(nm)O(nm),边的存储结构为
邻接矩阵。
- 朴素Dijkstra:贪心算法,必须保证无负权边,适合
- 多元最短路算法
- Floyd:动态规划,时间复杂度为O(n3)O(n^3)O(n3),边的存储结构为
邻接矩阵。
- Floyd:动态规划,时间复杂度为O(n3)O(n^3)O(n3),边的存储结构为
如果解析有不对之处还请指正,我会尽快修改,多谢大家的包容。
如果大家喜欢这个系列,还请大家多多支持啦😋!
如果这篇文章有帮到你,还请给我一个大拇指 👍和小星星 ⭐️支持一下白晨吧!喜欢白晨【算法】系列的话,不如关注👀白晨,以便看到最新更新哟!!!
我是不太能熬夜的白晨,我们下篇文章见。
相关文章:

【算法】最短路算法
😀大家好,我是白晨,一个不是很能熬夜😫,但是也想日更的人✈。如果喜欢这篇文章,点个赞👍,关注一下👀白晨吧!你的支持就是我最大的动力!Ǵ…...

< Linux > 进程间通信
目录 1、进程间通信介绍 进程间通信的概念 进程间通信的本质 进程间通信的分类 2、管道 2.1、什么是管道 2.2、匿名管道 匿名管道的原理 pipe函数 匿名管道使用步骤 2.3、管道的读写规则 2.4、管道的特点 2.5、命名管道 命名管道的原理 使用命令创建命名管道 mkfifo创建命名管…...

学习 Python 之 Pygame 开发魂斗罗(二)
学习 Python 之 Pygame 开发魂斗罗(二)魂斗罗的需求开始编写魂斗罗1. 搭建主类框架2. 设置游戏运行遍历和创建窗口3. 获取窗口中的事件4. 创建角色5. 完成角色更新函数魂斗罗的需求 魂斗罗游戏中包含很多个物体,现在要对这些物体进行总结 类…...
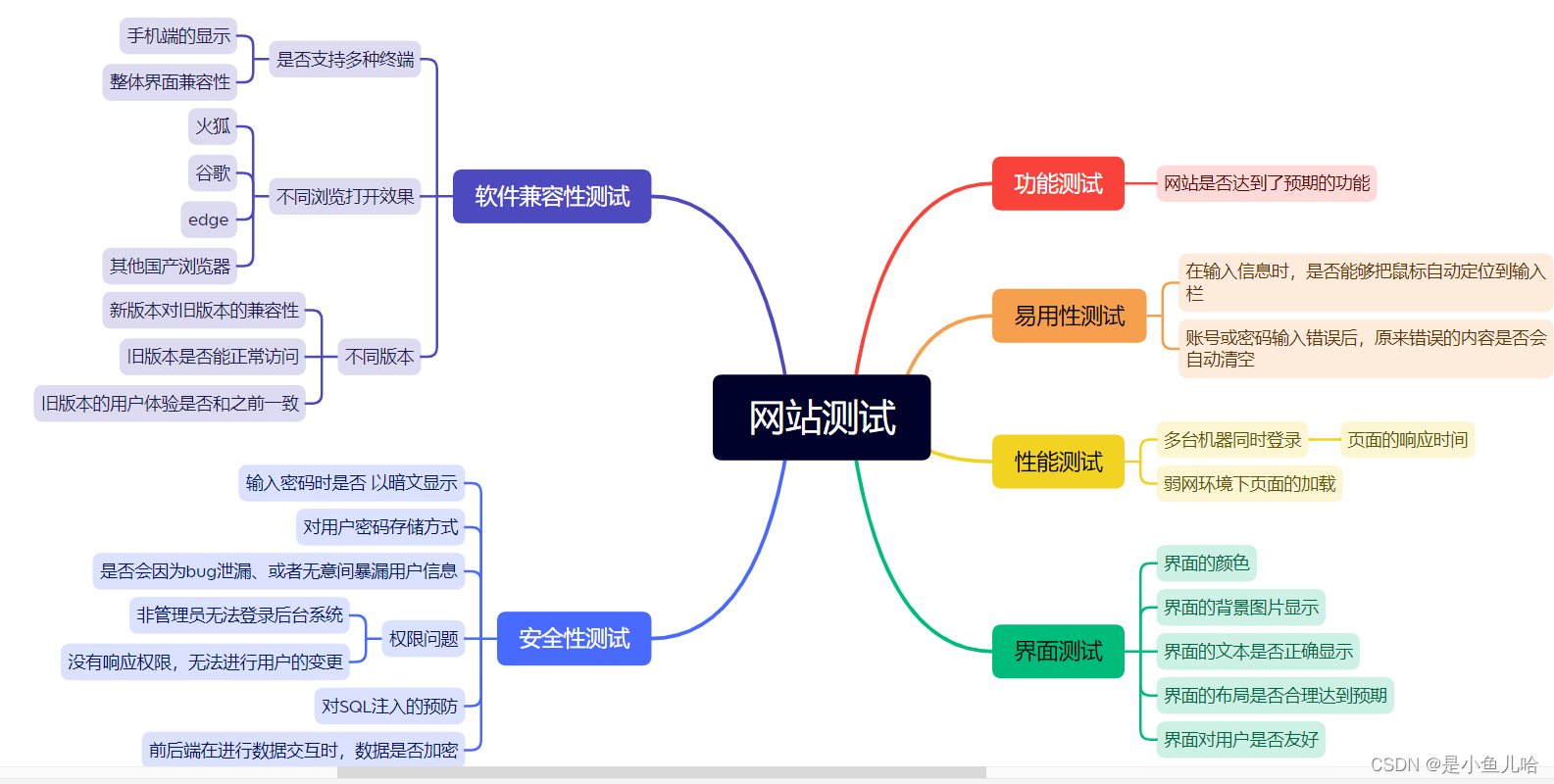
户籍管理系统测试用例
目录 一、根据页面的不同分别设计测试用例 登录页面 用户信息列表 用户编辑页面 用户更新页面 二、根据目的不同分别设计测试用例 一、根据页面的不同分别设计测试用例 上图是针对一个网站的测试,按照页面的不同分别来设计对应的测试用例。 登录页面 用户信息列…...
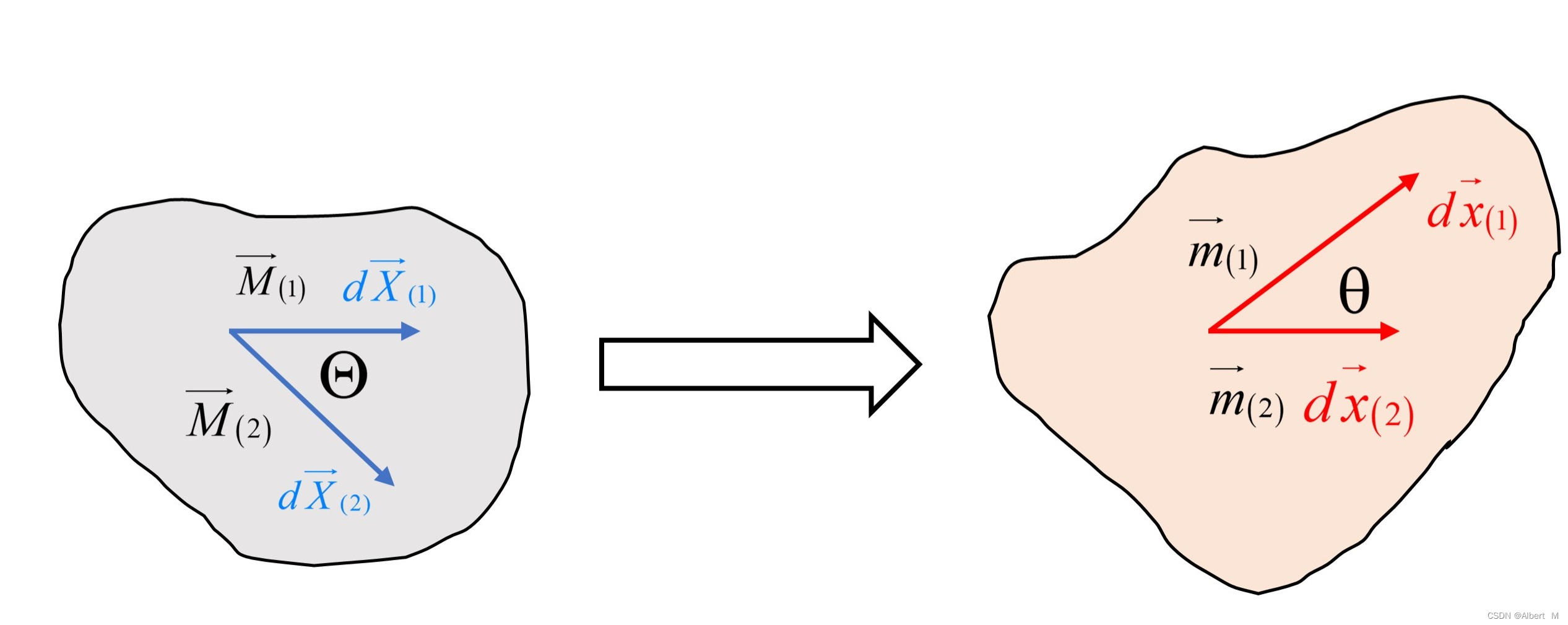
(三)代表性物质点邻域的变形分析
本文主要内容如下:1. 伸长张量与Cauchy-Green 张量2. 线元长度的改变2.1. 初始/当前构型下的长度比2.2. 主长度比与 Lagrange/Euler 主方向2.3. 初始/当前构型下任意方向的长度比3. 线元夹角的改变4. 面元的改变5. 体元的改变1. 伸长张量与Cauchy-Green 张量 由于变…...
Stream操作流 练习
基础数据:Data AllArgsConstructor NoArgsConstructor public class User {private String name;private int age;private String sex;private String city;private Integer money; static List<User> users new ArrayList<>();public static void m…...

【模拟集成电路】宽摆幅压控振荡器(VCO)设计
鉴频鉴相器设计(Phase Frequency Detector,PFD)前言一、VCO工作原理二、VCO电路设计VCO原理图三、压控振荡器(VCO)测试VCO测试电路图瞬态测试(1)瞬态输出(2)局部放大图&a…...

《英雄编程体验课》第 13 课 | 双指针
文章目录 零、写在前面一、最长不重复子串1、初步分析2、朴素算法3、优化算法二、双指针1、算法定义2、算法描述3、条件1)单调性2)时效性三、双指针的应用1、前缀和问题2、哈希问题3、K 大数问题零、写在前面 该章节节选自 《夜深人静写算法》,主要讲解最基础的枚举算法 ——…...

DS期末复习卷(十)
一、选择题(24分) 1.下列程序段的时间复杂度为( A )。 i0,s0; while (s<n) {ssi;i;} (A) O(n^1/2) (B) O(n ^1/3) © O(n) (D) O(n ^2) 12…xn xn^1/2 2.设某链表中最常用的…...

QT+OpenGL模板测试和混合
QTOpenGL模板测试和混合 本篇完整工程见gitee:QtOpenGL 对应点的tag,由turbolove提供技术支持,您可以关注博主或者私信博主 模板测试 当片段着色器处理完一个片段之后,模板测试会开始执行。和深度测试一样,它可能会丢弃片段&am…...

《英雄编程体验课》第 11 课 | 前缀和
文章目录 零、写在前面一、概念定义1、部分和2、朴素做法3、前缀和4、前缀和的边界值5、边界处理6、再看部分和二、题目描述1、定义2、求解三、算法详解四、源码剖析五、推荐专栏六、习题练习零、写在前面 该章节节选自 《算法零基础100讲》,主要讲解最基础的算法 —— 前缀和…...

Java学习--多线程2
2.线程同步 2.1卖票【应用】 案例需求 某电影院目前正在上映国产大片,共有100张票,而它有3个窗口卖票,请设计一个程序模拟该电影院卖票 实现步骤 定义一个类SellTicket实现Runnable接口,里面定义一个成员变量:privat…...
【Virtualization】Windows11安装VMware Workstation后异常处置
安装环境 Windows 11 专业版 22H2 build 22621.1265 VMware Workstation 17 Pro 17.0.0 build-20800274 存在问题 原因分析 1、BIOS未开启虚拟化。 2、操作系统启用的虚拟化与Workstation冲突。 3、操作系统启用内核隔离-内存完整性保护。 处置思路 1、打开“资源管理器”…...
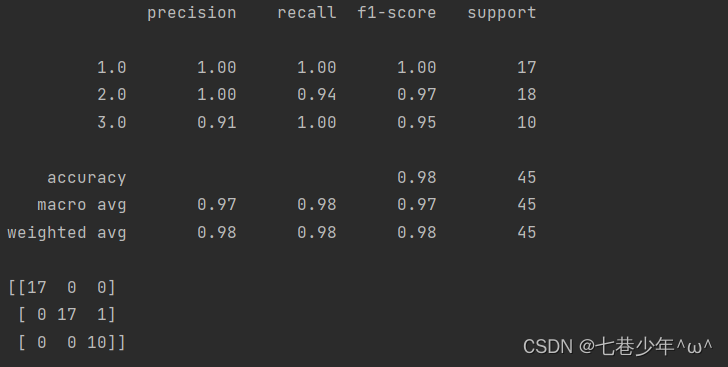
第四章.神经网络—BP神经网络
第四章.神经网络 4.3 BP神经网络 BP神经网络(误差反向传播算法)是整个人工神经网络体系中的精华,广泛应用于分类识别,逼近,回归,压缩等领域,在实际应用中,大约80%的神经网络模型都采用BP网络或BP网络的变化…...
如何压缩RAR格式文件?
RAR是我们日常生活工作中经常用到的压缩文件格式之一,那么RAR文件如何压缩呢? 不管压缩哪种格式的压缩文件,我们都需要用到压缩软件。针对RAR格式,我们可以选择最常见的WinRAR,当然如果有同样适用于RAR格式的压缩软件…...
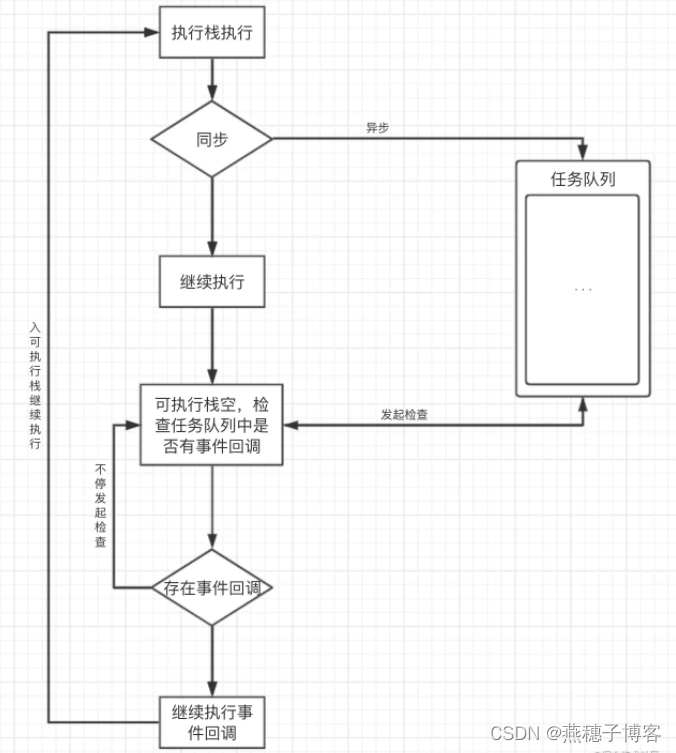
JS 执行机制 详解(附图)
一、JS是单线程JS语言的一大特点就是单线程,也就是说,同一个时间只能做一件事。这是JS这门脚本语言诞生的使命所致——用来处理页面中用户的交互,以及操作DOM而诞生的。单线程就意味着,所有任务需要排队,前一个任务结束…...
)
华为OD机试真题Java实现【 计算面积】真题+解题思路+代码(20222023)
计算面积 绘图机器的绘图笔初始位i在原点(0.0)。 机器启动后其绘图笔按下面规则绘制直线: 1 )尝试沿着横向坐标轴正向绘制直线,直到给定的终点值E, 2 )期间可通过指令在纵坐标轴方向进行偏移。井同时绘制直线,偏移后按规则1绘制直线;指令的格式为X offsetY。表示在横坐标X…...
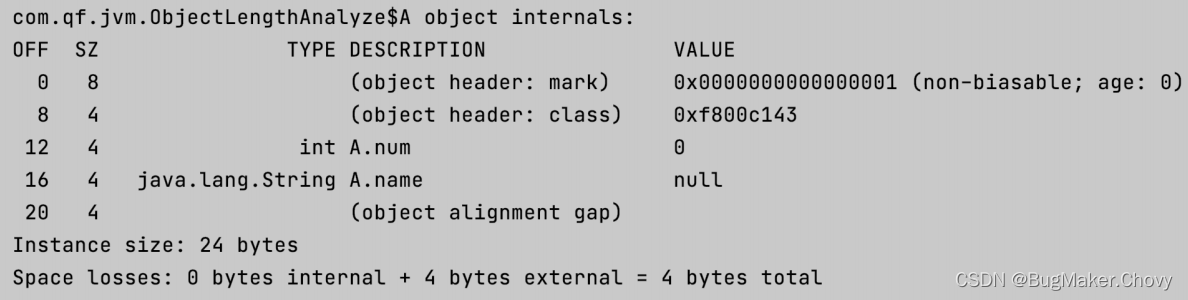
【JVM】运行时数据区与对象的创建流程
4、运行时数据区 4.1、运行时数据区介绍 运行时数据区也就是JVM在运⾏时产生的数据存放的区域,这块区域就是JVM的内存区域,也称为JVM的内存模型——JMM 堆空间(线程共享):存放new出来的对象 元空间(线程共…...
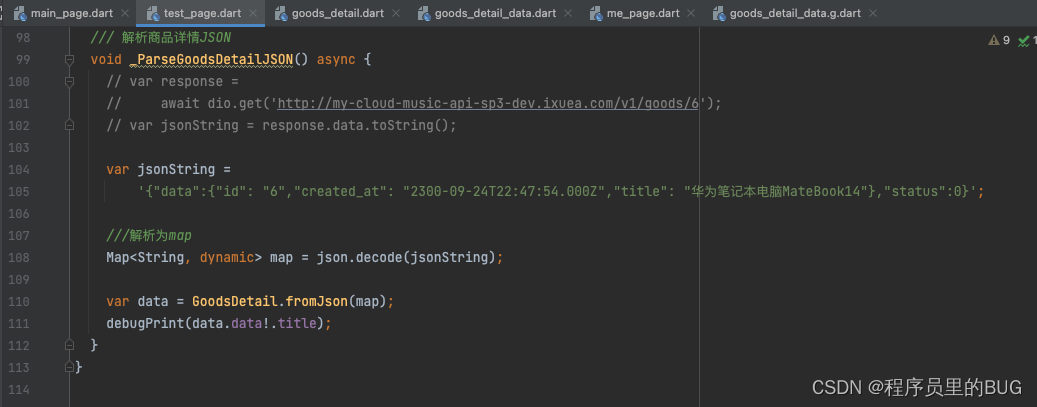
flutter- JSON解析框架使用方法json_serializable
对于目前来说,大部分的API网络请求的通讯内容数据格式都是JSON。JSON返回的都是字符串,假如要取到data里面的id,去直接字符串截取肯定是不行的,要通过一定的方式把它解析成Map或者解析成对象,再去处理它。像一些简单的…...
第十三届蓝桥杯国赛 C++ B 组 J 题——搬砖(AC)
目录1.搬砖1.题目描述2.输入格式3.输出格式4.样例输入5.样例输出6.数据范围7.原题链接2.解题思路3.Ac_code1.搬砖 1.题目描述 这天,小明在搬砖。 他一共有 nnn 块砖, 他发现第 iii 砖的重量为 wiw_{i}wi, 价值为 viv_{i}vi 。他突然想从这些 砖中选一些出来从…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
