经典文献阅读之--PLC-LiSLAM(面,线圆柱SLAM)
0. 简介
对于激光SLAM来说,现在越来越多的算法不仅仅局限于点线等简答特征的场景了,文章《PLC-LiSLAM: LiDAR SLAM With Planes, Lines,and Cylinders》说到,平面、线段与圆柱体广泛存在于人造环境中。为此作者提出了一个使用这些landmark的激光雷达SLAM系统。目前已有工作做了类似于BA的平面adjustment(即.PA),但是这类工作在缺少平面的场景效果很差,为了增强系统的鲁棒性,引入更多的特征是有必要的,因此作者在本文中引入了额外的线和圆柱体特征,并且实现了平面-线-圆柱体的adjustment即(PLCA),PLCA不依赖于从三维特征点捕获的点数,这使得高效求解大规模PLCA问题成为可能。定位部分通过将局部平面、直线和柱面与全局平面、直线和柱面来进行配准,从而进行实时姿态估计,这种被称为平面-直线-柱面配准(PLCR, plane-line-cylinder registration)。在检测landmark并完成数据关联的过程中很可能会引入误检。本文通过检查后端的成本(cost)函数来纠正这些错误,这个错误纠正机制是那些基于配准的方法。例如LOAM和ICP,由于它们并不维护数据间的关联关系,所以很难纠正这些错误。这里由于该论文没有预印本,所以作者以附录的形式展示了本文的内容。由于本文的内容较多,所以作者主要来讲解特征提取这块的内容。其余的用泡泡机器人的内容作为补充。
1. 文章贡献
在之前的工作[1],[2]中,我们探索了激光雷达SLAM的平面,并引入平面调整(PA,plane adjustment)来纠正漂移,这是视觉SLAM中的bundle adjustment(BA)的对应。由于只考虑平面,如果没有足够的平面进行姿态估计,这些方法将失败。本文扩展了我们[2]工作的内容,并加入了线条和圆柱体。具体来说,该算法包括局部映射、全局映射和定位三个部分。在局部和全局映射中,通过位姿联合优化平面、直线和圆柱体。我们将由此产生的最小二乘问题分别称为局部和全局平面-柱面调整(PLCA)。在定位中,通过使用平面、直线和柱面进行扫描到模型的连续时间配准来估计新的激光雷达扫描的姿态,称为连续时间平面-直线-柱面配准(PLCR)。本文的贡献如下:
-
本文证明,通过一些预处理,PLCA问题的求解与面、线以及圆柱体里的三维点的数量无关。因为这些landmark的表示是无边界的,许多三维点都会被包含在这些landmark里面。对于求解大尺度的PLCA问题,我们的方法行而有效。
-
本文提供了一个高效的PLCR问题求解方法。我们使用一阶泰勒展开来近似旋转,考虑到两帧之间的旋转一般是足够小的。如果比较大的旋转发生在两帧之间,我们进行迭代近似。
-
本文的算法能够容忍足够的检测误检测。因为遮挡以及激光雷达点云的稀疏性,检测这些landmark的过程容易引入误检测。这个错误纠正机制是那些基于配准的方法,例如LOAM以及ICP很难做到的,因为他们并不维护数据关联。我们的算法通过检验后端的cost来纠正这些误检测。
2. 详细内容
2.1 前后端概念
-
位姿:这个公式表示通过转换矩阵X=[Rt01]∈SE(3)X = \left[ \begin{matrix} R&t\\0&1\end{matrix}\right]∈SE(3)X=[R0t1]∈SE(3)将局部LiDAR坐标系中的点坐标转换到全局坐标系中的一个姿态。其中∈SO(3)∈SO(3)∈SO(3)为旋转矩阵,t∈R3t∈\mathbb{R}^3t∈R3为平移向量。在PLCR和PLCA中,xxx参数为x=[ω;t]x = [ω;t]x=[ω;t],其中ωωω代表了RRR的角轴(angle-axis)表示形式:
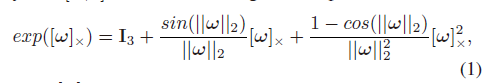
其中[ω]×[ω]_×[ω]×表示ωωω的斜对称矩阵,∣∣ω∣∣2||ω||_2∣∣ω∣∣2表示ωωω的L2L^2L2范数。 -
平面:本文中的平面通过一个四维向量表示。前三维表示该平面的法向量,模长为1,最后一维为坐标系原点到该平面的距离。我们将平面表示为π=[n;d]π = [\mathbf{n};d]π=[n;d],其中n\mathbf{n}n为∣∣n∣∣2=1||\mathbf{n}||_2 = 1∣∣n∣∣2=1的平面法线,∣d∣|d|∣d∣为原点到该平面的距离。在PLCA中,πππ用最近点参数化η=dnη = d\mathbf{n}η=dn表示[27]。
-
线:本文中的直线通过一个六维向量表示。前三维表示该直线的方向,后三维表示从原点出发的,垂直于该直线的向量,并且其模长为原点到直线的距离。文中用普吕克坐标(Plücker坐标)[28]表示一条三维空间中的直线,它是一个六维向量l=[d;m]l = [d;m]l=[d;m],其中ddd是lll的方向,∣∣d∣∣2=1||d||_2 = 1∣∣d∣∣2=1, mmm垂直于由原点和lll确定的平面,∣∣m∣∣2||m||_2∣∣m∣∣2等于从原点到lll的距离,lll有四个自由度。在PLCA中,我们采用[29]中引入的方法对lll进行参数化。具体来说,给定lll,我们首先构造一个旋转矩阵Rl=[d,m∣∣m∣∣2,d×m∣∣m∣∣2]R^l = [d, \frac{m}{||m||_2}, d × \frac{m}{||m||_2}]Rl=[d,∣∣m∣∣2m,d×∣∣m∣∣2m],其中×××为叉积。假设ωlω^lωl是(1)中RlR^lRl的角轴表示,我们可以用一个四维向量将lll参数化ζ=[ωl;∣∣m∣∣2]ζ = \left[ω^l; | |m| |_ 2 \right]ζ=[ωl;∣∣m∣∣2]。
-
圆柱体:本文中的圆柱体通过一个七维向量表示,前六维为该圆柱体所在的直线表示(同上),最后一维为该圆柱体的半径。文中将圆柱体表示为c=[lc;r]c = [l^c;r]c=[lc;r],其中lcl^clc为ccc中线的Plücker坐标,rrr为其半径。在PLCA中,我们通过一个五维向量ν=[ζc;r]ν = \left[ζ^c;r\right]ν=[ζc;r]来完成参数化;其中ζζζ是上面定义的lcl^clc的参数化。
-
观察:用mmm表示平面、直线或圆柱体,即m∈{π,l,c}m∈\{π, l, c\}m∈{π,l,c}。其中mjm_jmj表示为第jjj个landmark特征点信息。并且认为mjm_jmj在XiX_iXi处是可观测的,mjm_jmj在XiX_iXi处的观测值形成一组NijmN^m_{ij}Nijm点,表示为Pijm={pijkm}k=1Nijm\mathbb{P}^m_{ij} = \{p^m_{ijk}\}^{N^m_{ij}} _{k=1}Pijm={pijkm}k=1Nijm。我们将pijkmp^m_{ijk}pijkm的齐次坐标表示为p~ijkm=[pijkm;1]\tilde{p}^m_{ijk} = [p^m_{ijk}; 1]p~ijkm=[pijkm;1]。将Pijm\mathbb{P}^m_{ij}Pijm中各点的同质坐标堆叠起来,我们就会得到一个Pijm×4\mathbb{P}^m_{ij}× 4Pijm×4的矩阵
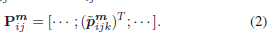
由于平面、直线和圆柱体是无界物体,NijmN^m_{ij}Nijm可能非常大,这导致了大规模的最小二乘问题。 -
优化:Levenberg-Marquardt(LM)[30]算法通常用于解决最小二乘问题。给定一个最小二乘问题 χ^=argmin∣∣(χ)∣∣22\hat{χ} = \arg\min||(χ)||^2_2χ^=argmin∣∣(χ)∣∣22,LM算法在第kkk次迭代时通过χk+1=χk+Δχ_{k+1} = χ_{k} + Δχk+1=χk+Δ更新解决方案。这里的ΔΔΔ是以下线性方程组的解
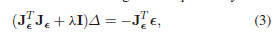
其中JεJ_\varepsilonJε是在χkχ_kχk处的雅各布矩阵,λλλ是LMalgorithm的参数,在每次迭代时都要调整,以确保∣∣(χ)∣∣22||(χ)||^2_2∣∣(χ)∣∣22的值减少。为了应用LM算法,我们通常先计算JεJ_\varepsilonJε和ε\varepsilonε,然后将其代入(3)来计算ΔΔΔ。 因为 N^m_{ij}可能非常大,这种直接的方法可能是计算上的要求。另一方面,显而易见的是 只需要JεTJεJ_\varepsilon^TJ_\varepsilonJεTJε和JεTεJ_\varepsilon^T \varepsilonJεTε就可以得到varDeltavarDeltavarDelta。我们表明 PLCA的JεTJεJ_\varepsilon^TJ_\varepsilonJεTJε和JεTεJ_\varepsilon^T \varepsilonJεTε有特殊的结构,可以用来加速计算。用来加速计算。
-
二次方形式:一个对称矩阵A=[aij]∈Rn×nA=[a_{ij}]∈\mathbb{R}^{n×n}A=[aij]∈Rn×n决定了一个二次形式qA=yTAyq_A=y^TAyqA=yTAy,其中y=[y1;...;yn]y=[y1; ...; yn]y=[y1;...;yn]。我们可以把qAq_AqA写成
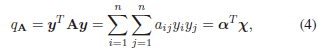
其中χ=[−−−;yiyj;−−](i≤j),α=[−−−;cijaij;−−]χ = [ - - - ; y_iy_j ; - - ] (i ≤ j),α = [ - - - ; c_{ij}a_{ij} ; - - ]χ=[−−−;yiyj;−−](i≤j),α=[−−−;cijaij;−−] (如果i=ji = ji=j,cij=1c_{ij} = 1cij=1,并且(i<j),cij=2(i < j),cij = 2(i<j),cij=2)。 -
矩阵计算:假设z=[z1;...;zm]z = [z1; ...; zm]z=[z1;...;zm],zzz是上面定义的yyy的向量函数。假设P∈Rk×mP∈\mathbb{R}^{k×m}P∈Rk×m是一个恒定的k×mk×mk×m矩阵。让我们定义f=Pzf = P_zf=Pz,并将fff的雅各布矩阵表示为JfJ_fJf。根据矩阵计算规则,JfJ_fJf的形式为
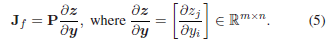
这里∂z∂y\frac{∂_z}{∂_y}∂y∂z是一个m×nm×nm×n的矩阵,∂zj∂yi\frac{∂_{z_j}}{∂_{y_i}}∂yi∂zj是∂z∂y\frac{∂_z}{∂_y}∂y∂z的第iii行和第jjj列的条目。
2.2 系统总览
本文提出的系统由前端与后端组成,前端检测面、线与圆柱体,并建立局部到全局的数据关联,从而进行后续的位姿估计。前端也决定了什么时候一个新的关键帧应当被创建。后端包括局部与全局的PLCA。局部的PLCA通过滑窗优化位姿与landmark。全局的PLCA优化所有的PLCA以及除了第一帧外的所有位姿。当有Landmark被再次观测到时,全局的PLCA便会被触发。

2.3 前端
-
Landmark检测:对激光雷达每一条线的数据进行切分:类似于LOAM,计算每个三维点的曲率,并将属于edge点的部分提取出来,组成集合E\mathbb{E}E。以每条线上每两个edge点作为两端,可以把这条线分为许多段,这些段里的点为平坦点,组成集合F\mathbb{F}F。
平面与圆柱体检测:对于每个线上的每段平坦点,寻找与其相近的,但不属于同一条线上的平坦点,如果用RANSAC法拟合平面的平均误差比较小,则利用平面模型来拟合,否则用圆柱体来拟合这些点。
直线检测:对每个段里的edge点,找到所有与其相近的,但属于另一条线的edge点ppp。利用这两个点可以求得直线方程。对ppp点再寻找一个在其他线的最近点p2p_2p2。如果p2p_2p2到该直线的距离足够小,则利用这三个点来拟合一条直线。重复这个过程直到没有点能够被加入到直线中。
-
Landmark关联
当新一帧点云获得后,首先计算属于该帧的集合E\mathbb{E}E与集合F\mathbb{F}F。并对这两个集合分别构建KD-tree。对上一帧里的每个点ppp,寻找其在当前帧的nnn个最近点。如果ppp属于面或者圆柱体,则这nnn个最近点都被保留,如果ppp属于直线,则保留这n个点的曲率最大的一个点。随后,利用RANSAC算法找到符合模型的内殿。通过这些内点,我们之后会使用PLCR方法来进行位姿估计。 -
关键帧创建
受到ORB-SLAM的启发,当以下情况发生时,新的关键帧会被创建:- 当前帧20%以上的点不能被追踪与关联。
- 当前帧与上一个关键帧的旋转角度大于5°。
- 当前帧与上一帧的距离大于设定的阈值。
对于新的关键帧,我们在没被关联到的三维点上检测面、线与圆柱体。对于新检测出来的landmark,首先会寻找与已有的landmark的均方根之差,如果大于设定的阈值,则新增一个landmark。
2.4 面-线-圆柱体 联合优化 (PLCA)
-
全局PLCA
在全局的PLCA中,对所有点计算点到模型的损失,从而构建优化问题来同时优化位姿与landmark的参数。作者详细给出了各个模型的LM优化时的参数的形式,有兴趣的同学可以阅读原文,这里不再赘述。
作者证明,构建优化问题Ax=b时,A的规模仅与Landmark的数量有关,而与landmark里的点的数量无关。
…详情请参照古月居
相关文章:

经典文献阅读之--PLC-LiSLAM(面,线圆柱SLAM)
0. 简介 对于激光SLAM来说,现在越来越多的算法不仅仅局限于点线等简答特征的场景了,文章《PLC-LiSLAM: LiDAR SLAM With Planes, Lines,and Cylinders》说到,平面、线段与圆柱体广泛存在于人造环境中。为此作者提出了一个使用这些landmark的…...

计算组合数Cnk即从n个不同数中选出k个不同数共有多少种方法math.comb(n,k)
【小白从小学Python、C、Java】 【计算机等级考试500强双证书】 【Python-数据分析】 计算组合数Cnk 即从n个不同数中选出k个不同数共有多少种方法 math.comb(n,k) 以下python代码输出结果是? import math print("【执行】print(math.comb(3,1))") print(math.comb(…...

工厂设计模式
基本概念:为创建对象提供过渡接口,以便将创建对象的具体过程屏蔽隔离起来,达到提高灵活性的目的。分为三类:简单工厂模式Simple Factory:不利于产生系列产品;工厂方法模式Factory Method:又称为…...
IO多路转接 —— poll和epoll
文章目录1. poll1.1 poll的函数接口1.2 poll的简单测试程序1.3 poll的优缺点分析2. epoll2.1 epoll的函数接口2.2 epoll的工作原理2.3 epoll的工作模式(LT,ET)2.4 epoll的简易服务器实现(默认是LT工作模式)前言: 接上文讲述的select,它有缺点,…...

计算机网络整理-问答
1. 程序工作的时候网络各层的状态 如下图所示: 1. TCP 在进行三次握手的时候,IP 层和 MAC 层对应都有什么操作呢? TCP 三次握手是通过在传输层建立连接的一个过程,在这个过程中,TCP 和 IP 层、MAC 层都起到了重要的…...
JS 实现抛物线动画案例
相信大家都有浏览过,很多购物网站购物车的添加商品动画,今天,我们就手写一个简单的抛物线动画,先上案例: 一、绘制页面 我们这里简单实现,一个按钮,一个购物车图标,样式这里直接跳过…...
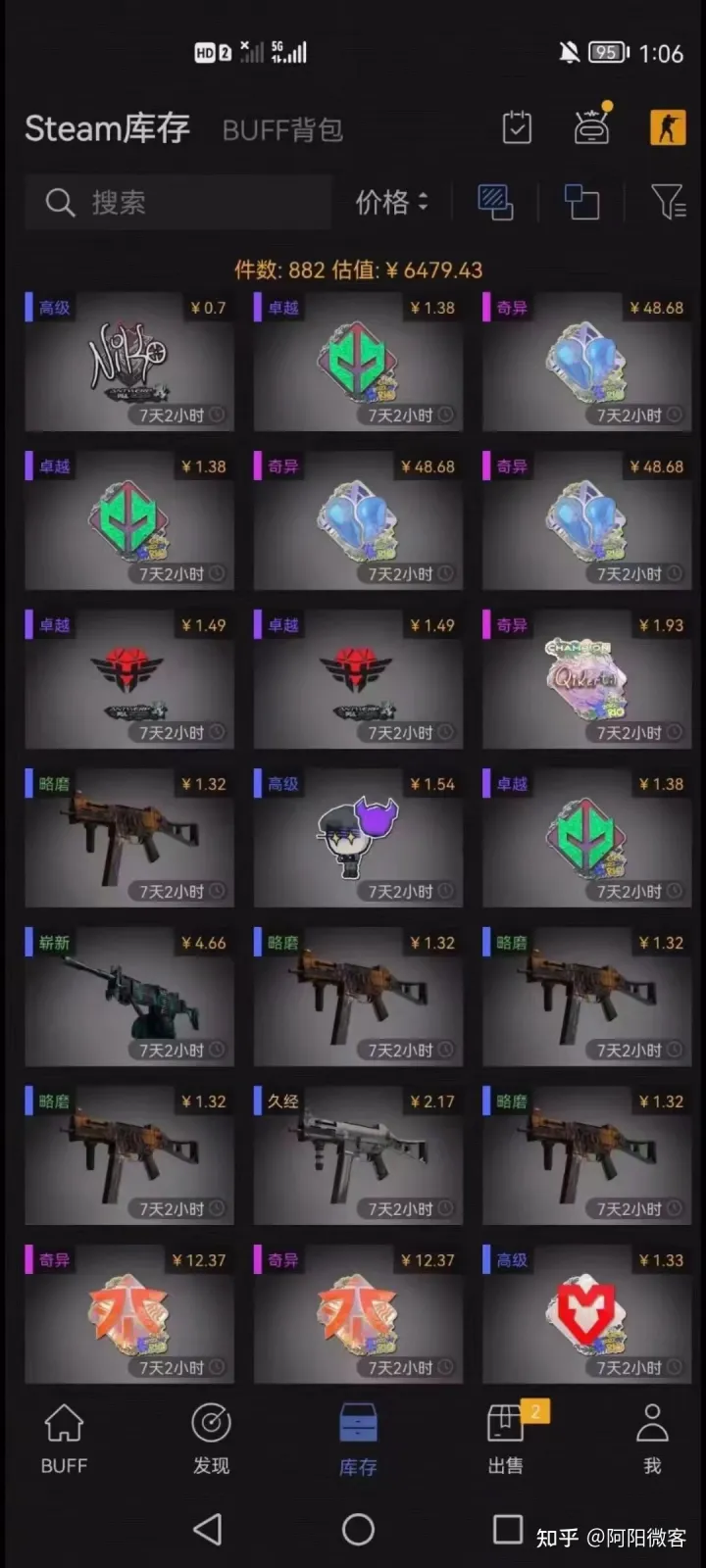
CSGO搬砖项目,23年最适合小白的项目!
大家好,我是阿阳 不懂的小伙伴,咱继续听我娓娓道来 steam搬砖主要涉及的是csgo游戏平台装备的一个搬运,比较很好理解,主要就是道具的搬运工,简单来讲就是,从国外steam游戏平台购买装备,再挂到…...
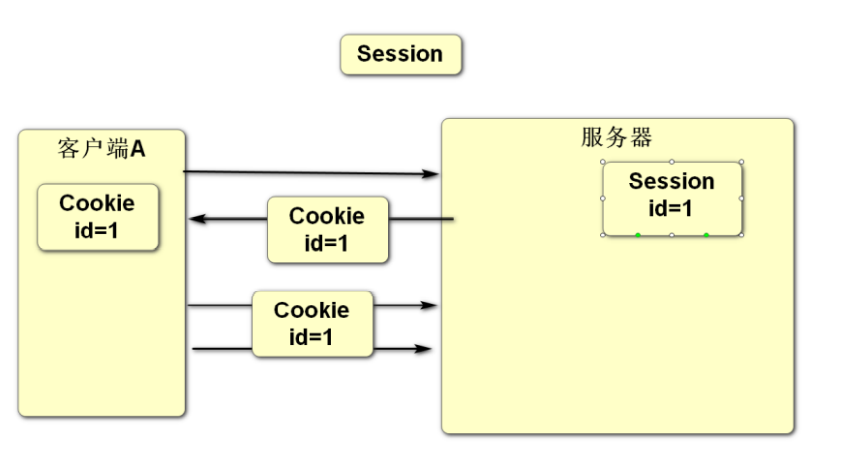
谈谈会话管理
客户端和服务器之间进行数据传输遵循的是HTTP协议, 此协议属于无状态协议(一次请求对应一次响应, 响应完之后断开连接), 服务器是无法跟踪客户端的请求, 通过cookie技术可以给客户端添加一个标识, 客户端之后发出的每次请求都会带着这个标识从而让服务器识别此客户端, 但由于co…...
Linux查看JVM FULL GC频率
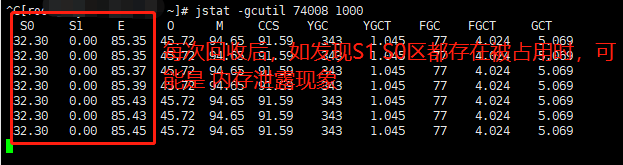
查看系统的full gc频率,可以使用jstack命令一、采用top命令定位进程登录服务器,执行top命令,查看CPU占用情况,找到进程的pid二、使用jstack命令统计垃圾回收jstat -gc pid 5000即会每5秒一次显示进程号为pid的java进程的GC情况以上…...

java世界String的那些事
String的创建机理: 由于String在Java世界中使用过于频繁,Java为了避免在一个系统中产生大量的String对象,引入了字符串常量池。其运行机制是:创建一个字符串时,首先检查池中是否有值相同的字符串对象,如果…...

【图像配准】多图配准/不同特征提取算法/匹配器比较测试
前言 本文首先完成之前专栏前置博文未完成的多图配准拼接任务,其次对不同特征提取器/匹配器效率进行进一步实验探究。 各类算法原理简述 看到有博文[1]指出,在速度方面SIFT<SURF<BRISK<FREAK<ORB,在对有较大模糊的图像配准时&…...
2023金三银四季跳槽季,啃完这软件测试面试题,跳槽不就稳稳的了
前言 2023年也到来了,接近我们所说的“金三银四”也正在执行了,时间晃眼就过去了,有的人为了2023跳槽早早做足了准备,有的人在临阵磨刀,想必屏幕前的你也想在2023年涨薪吧,那么问题来了,怎么才…...
【C++详解】——vector类
📖 前言:本期介绍vector类。 目录🕒 1. vector的介绍🕒 2. vector的使用🕘 2.1 定义🕘 2.2 iterator🕘 2.3 空间增长🕘 2.4 增删查改🕒 2. vector的模拟实现🕘…...
uniapp 离线本地打包
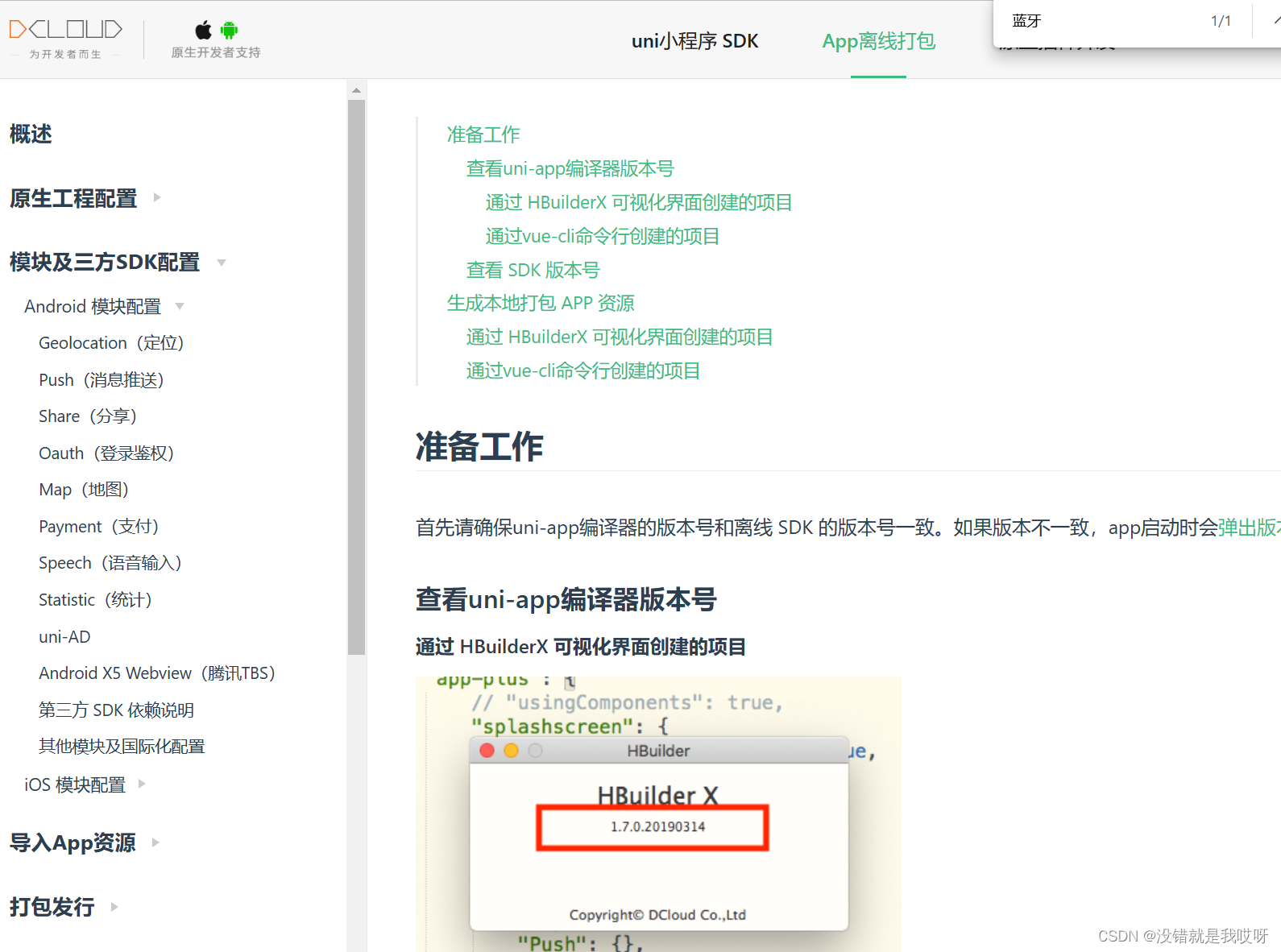
uniapp打包教程地址 https://nativesupport.dcloud.net.cn/AppDocs/usesdk/android.html点击查看 需要的环境: java (1.8)离线SDK(上面的连接下载即可)Android Studio(同上) 配置环境变量 依次点击“计算机”-“属性”&#…...
)
初识马尔科夫模型(Markov Model)
初识马尔科夫模型(Markov Model)一、概念二、性质三、学习步骤一、概念 马尔科夫模型(Markov Model)是一种概率模型,用于描述随机系统中随时间变化的概率分布。马尔科夫模型基于马尔科夫假设,即当前状态只…...
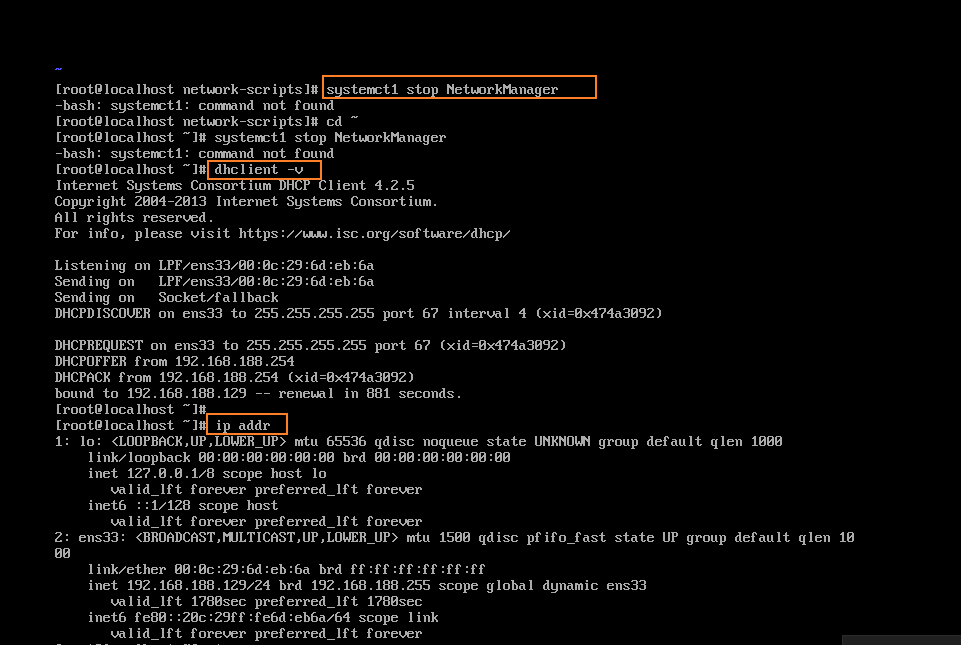
CentOS7 ifconfig(或 ip addr)命令不显示IP地址
问题(因为当时没有存图 所以这个图上是网上找的 )解决办法第一:可能是本地服务没有开启,检查本地服务。如图所示,检查这两个服务是否开启。注:如何快速找到服务 可以把光标放在其中一个上面 然后按下VM就可…...

2023/2/10总结
拓扑排序 拓扑排序是在一个有向无环图(DAG)所有顶点的线性排序。 拓扑排序核心思想非常简单,就是先找一个入度为0的顶点输出,再从图中删除该顶点和以它为起点的有向边。继续上面的操作知道所有的顶点访问完为止。 入度…...

2023最新版!宝塔面板Docker自建Bitwarden密码管理
Powered by:NEFU AB-IN 请一定要结合B站视频食用!!!!,下面的博客总体来说只是起到提纲作用 B站视频链接!!! 文章目录2023最新版!宝塔面板Docker自建Bitwarden密码管理前…...

【Hello Linux】 Linux基础命令
作者:小萌新 专栏:Linux 作者简介:大二学生 希望能和大家一起进步! 本篇博客简介:介绍Linux的基础命令 Linux基础命令ls指令lsls -als -dls -ils -sls -lls -nls -Fls -rls -tls -Rls -1总结思维导图pwd指令whoami指令…...
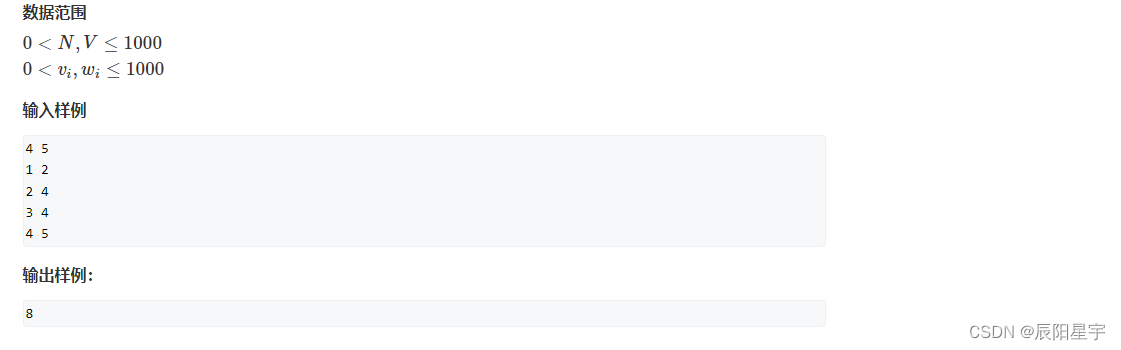
151、【动态规划】leetcode ——2. 01背包问题:二维数组+一维数组(C++版本)
题目描述 原题链接:2. 01背包问题 解题思路 (1)二维dp数组 动态规划五步曲: (1)dp[i][j]的含义: 容量为j时,从物品1-物品i中取物品,可达到的最大价值 (2…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

Appium下载安装配置保姆教程(图文详解)
目录 一、Appium软件介绍 1.特点 2.工作原理 3.应用场景 二、环境准备 安装 Node.js 安装 Appium 安装 JDK 安装 Android SDK 安装Python及依赖包 三、安装教程 1.Node.js安装 1.1.下载Node 1.2.安装程序 1.3.配置npm仓储和缓存 1.4. 配置环境 1.5.测试Node.j…...

CSS 工具对比:UnoCSS vs Tailwind CSS,谁是你的菜?
在现代前端开发中,Utility-First (功能优先) CSS 框架已经成为主流。其中,Tailwind CSS 无疑是市场的领导者和标杆。然而,一个名为 UnoCSS 的新星正以其惊人的性能和极致的灵活性迅速崛起。 这篇文章将深入探讨这两款工具的核心理念、技术差…...
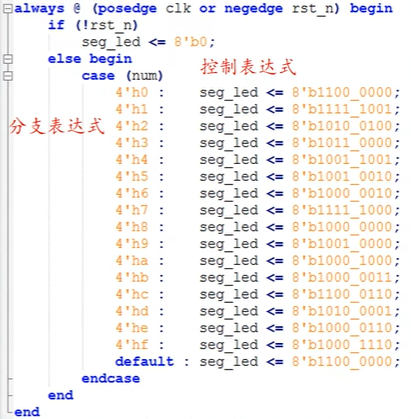
ZYNQ学习记录FPGA(二)Verilog语言
一、Verilog简介 1.1 HDL(Hardware Description language) 在解释HDL之前,先来了解一下数字系统设计的流程:逻辑设计 -> 电路实现 -> 系统验证。 逻辑设计又称前端,在这个过程中就需要用到HDL,正文…...
本地部署drawDB结合内网穿透技术实现数据库远程管控方案
文章目录 前言1. Windows本地部署DrawDB2. 安装Cpolar内网穿透3. 实现公网访问DrawDB4. 固定DrawDB公网地址 前言 在数字化浪潮席卷全球的背景下,数据治理能力正日益成为构建现代企业核心竞争力的关键因素。无论是全球500强企业的数据中枢系统,还是初创…...
