球面坐标系下的三重积分
涉及知识点
- 三重积分
- 球面坐标系
- 点火公式
- 一些常见积分处理手法
球面坐标系定义
球面坐标系由方位角φ\varphiφ、仰角θ\thetaθ和距离rrr构成
直角坐标系(x,y,z)(x,y,z)(x,y,z)到球面坐标系的(r,φ,θ)(r,\varphi,\theta)(r,φ,θ)的转化规则如下:
{x=rsinφcosθy=rsinθsinφz=rcosφ\left\{ \begin{aligned} x & = & r\sin φ\cosθ \\ y & = & r\sin θ\sin φ \\ z & = & r\cos φ \end{aligned} \right. ⎩⎨⎧xyz===rsinφcosθrsinθsinφrcosφ

适用
适用于积分区域为球或球的部分、锥或锥的部分。
处理方法
按规则直角坐标系的积分式转换成球面坐标系就行
∭Ωf(x,y,z)dxdydz=∭Ωf(rsinφcosθ,rsinθsinφ,rcosφ)r2sinφdθdφdr\iiint \limits_{\Omega} f(x,y,z)dxdydz=\iiint \limits_{\Omega}f(r\sin φ\cosθ,r\sin θ\sin φ,r\cos φ)r^2\sin \varphi d\theta d\varphi drΩ∭f(x,y,z)dxdydz=Ω∭f(rsinφcosθ,rsinθsinφ,rcosφ)r2sinφdθdφdr
然后一般按如下顺序写出积分式:
∫dθ∫dφ∫f(r,θ,φ)dr\int d\theta \int d\varphi \int f(r,\theta,\varphi)dr∫dθ∫dφ∫f(r,θ,φ)dr
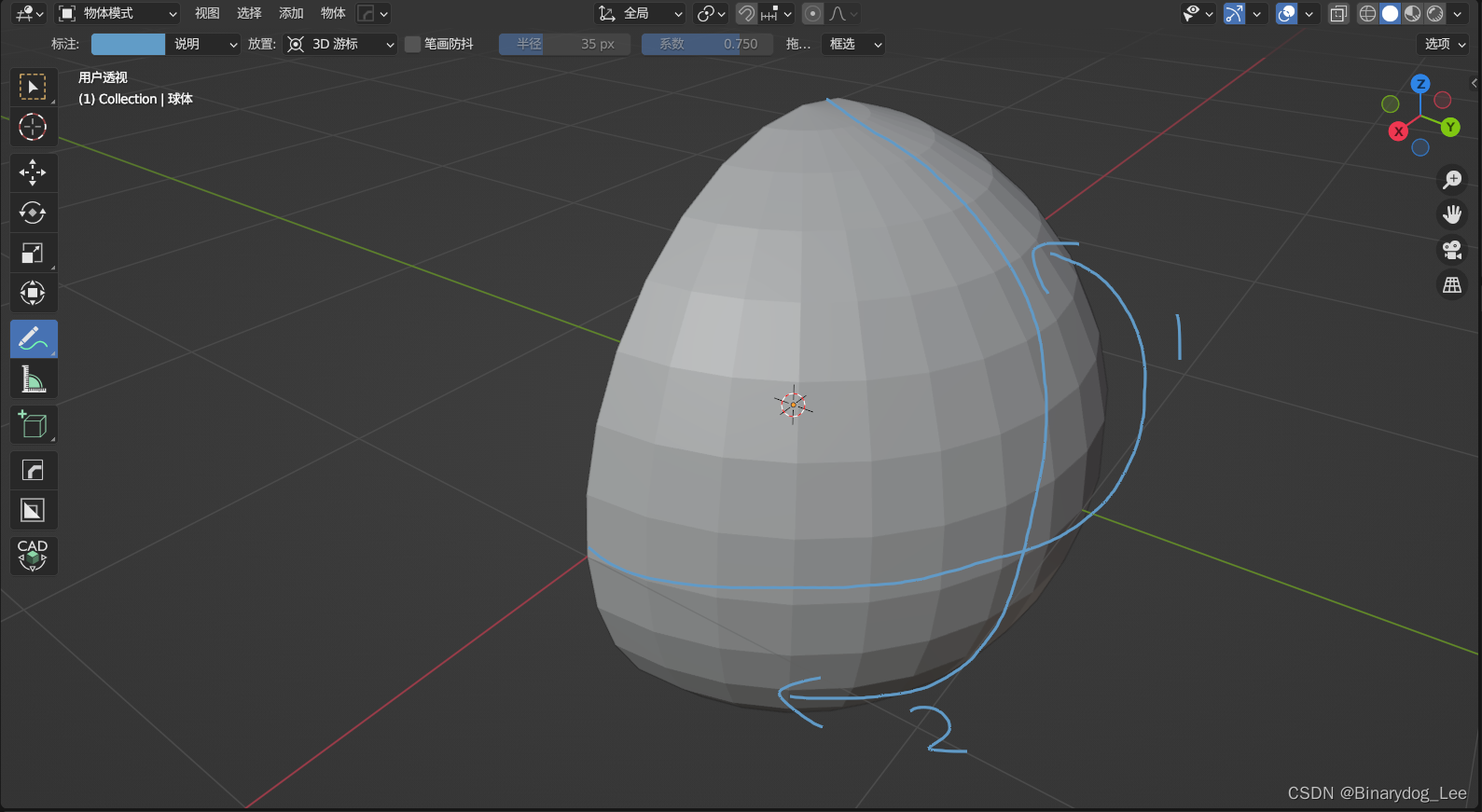
由于“后积先定限”,所以先处理方位角,即下图中1的轨迹,随后处理仰角,即下图中2的轨迹,两个角取值范围都是[0,2π][0,2\pi][0,2π]
例题
计算三重积分∭Ω(x2+y2)dv\iiint \limits_{\Omega}(x^2+y^2)dvΩ∭(x2+y2)dv其中Ω\OmegaΩ是右半球面x2+y2+z2=a2(y≥0,a>0)x^2+y^2+z^2=a^2\text{ }(y\ge 0,a>0)x2+y2+z2=a2 (y≥0,a>0)与xOzxOzxOz面所围成的区域
【解析】
Ω={0≤r≤a,0≤θ≤π,0≤φ≤π}\Omega = \{0\le r\le a,0\le \theta \le \pi,0\le \varphi \le \pi \}Ω={0≤r≤a,0≤θ≤π,0≤φ≤π}
本题即解如下积分
∭Ωr2sin2φ⋅r2sinφdrdθdφ\iiint \limits_{\Omega}r^2\sin^2\varphi ·r^2\sin \varphi drd\theta d\varphiΩ∭r2sin2φ⋅r2sinφdrdθdφ
即:
∫0πdθ∫0πdφ∫0ar4sin3φdr\int_0^\pi d\theta \int_0^\pi d\varphi \int_0^a r^4\sin^3\varphi dr∫0πdθ∫0πdφ∫0ar4sin3φdr
其中在drdrdr时sin3φ\sin^3\varphisin3φ是常量,可提出,剩下就是对r4r^4r4积分,即变为:
∫0πdθ∫0πsin3φ⋅a55dφ\int_0^\pi d\theta \int_0^\pi \sin^3\varphi · \frac{a^5}{5} d\varphi∫0πdθ∫0πsin3φ⋅5a5dφ
a55\frac{a^5}{5}5a5是常数可提出,并且这个对φ\varphiφ积分完要对θ\thetaθ积分,可以先变换顺序先对θ\thetaθ积分,则原式变为:
π5a3∫0πsin3φdφ\frac{\pi}{5}a^3 \int_0^\pi \sin^3\varphi d\varphi5πa3∫0πsin3φdφ
对于sin3φ\sin^3\varphisin3φ的积分步骤中用到了点火公式,过程如下:
∫0πsin3φdφ=∫0π2sin3φdφ+∫π2πsin3φdφ=23+∫π2πsin3φdφ\int_0^\pi \sin^3\varphi d\varphi=\int_0^{\frac\pi 2} \sin^3\varphi d\varphi+\int_{\frac\pi 2}^\pi \sin^3\varphi d\varphi=\frac23+\int_{\frac\pi 2}^\pi \sin^3\varphi d\varphi∫0πsin3φdφ=∫02πsin3φdφ+∫2ππsin3φdφ=32+∫2ππsin3φdφ
对于右侧的积分继续进行处理,令φ=π−t\varphi = \pi - tφ=π−t(好像算是区间再现公式)
∫π2πsin3φdφ=∫π20sin3(π−t)d(π−t)=∫π20sin3(π−t)d(−t)\int_{\frac\pi 2}^\pi \sin^3\varphi d\varphi=\int_{\frac\pi 2}^0 \sin^3(\pi - t) d(\pi - t)= \int_{\frac\pi 2}^0 \sin^3(\pi - t) d(- t)∫2ππsin3φdφ=∫2π0sin3(π−t)d(π−t)=∫2π0sin3(π−t)d(−t)
提出负号,上下限颠倒,则右侧积分式等于:
∫0π2sin3(π−t)dt\int_0^{\frac\pi 2} \sin^3(\pi - t) dt∫02πsin3(π−t)dt
根据sin3x\sin^3xsin3x的对称性,该式子又等于:
∫0π2sin3tdt=23\int_0^{\frac\pi 2} \sin^3t dt=\frac23∫02πsin3tdt=32
故原式等于
π5a3∫0πsin3φdφ=π5a3⋅(23+23)=415πa5\frac{\pi}{5}a^3 \int_0^\pi \sin^3\varphi d\varphi=\frac{\pi}{5}a^3·(\frac 23+\frac 23)=\frac4{15}\pi a^55πa3∫0πsin3φdφ=5πa3⋅(32+32)=154πa5
即最终结果
相关文章:

球面坐标系下的三重积分
涉及知识点 三重积分球面坐标系点火公式一些常见积分处理手法 球面坐标系定义 球面坐标系由方位角φ\varphiφ、仰角θ\thetaθ和距离rrr构成 直角坐标系(x,y,z)(x,y,z)(x,y,z)到球面坐标系的(r,φ,θ)(r,\varphi,\theta)(r,φ,θ)的转化规则如下: {xrsinφco…...

谷歌 Jason Wei | AI 研究的 4 项基本技能
文章目录 一、前言二、主要内容三、总结CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 原文作者为 Jason Wei,2020 年达特茅斯学院本科毕业,之后加入 Google Brain 工作。 Jason Wei 的博客主页:https://www.jasonwei.net/ 其实我不算是一个特别有经验的研究员…...

excel数据整理:合并计算快速查看人员变动
相信大家平时在整理数据时,都会对比数据是否有重复的地方,或者该数据与源数据相比是否有增加或者减少。数据量不大还好,数据量大的话,对比就比较费劲了。接下来我们将进入数据对比系列课程的学习。该系列一共有两篇教程࿰…...

vit-pytorch实现 MobileViT注意力可视化
项目链接 https://github.com/lucidrains/vit-pytorch 注意一下参数设置: Parameters image_size: int. Image size. If you have rectangular images, make sure your image size is the maximum of the width and heightpatch_size: int. Number of patches. im…...

Python将字典转换为csv
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。喜欢通过博客创作的方式对所学的知识进行总结与归纳,不仅形成深入且独到的理…...
EasyX精准帧率控制打气球小游戏
🎆音乐分享 New Boy —— 房东的猫 之前都用Sleep()来控制画面帧率,忽略了绘制画面的时间 如果绘制画面需要很长的时间,那么就不能忽略了。 并且Sleep()函数也不是特别准确,那么就…...

你知道 GO 中什么情况会变量逃逸吗?
你知道 GO 中什么情况会变量逃逸吗?首先我们先来看看什么是变量逃逸 Go 语言将这个以前我们写 C/C 时候需要做的内存规划和分配,全部整合到了 GO 的编译器中,GO 中将这个称为 变量逃逸 GO 通过编译器分析代码的特征和代码的生命周期&#x…...

一篇文章学懂C++和指针与链表
指针 目录 指针 C的指针学习 指针的基本概念 指针变量的定义和使用 指针的所占的内存空间 空指针和野指针 const修饰指针 指针和数组 指针和函数 指针、数组、函数 接下来让我们开始进入学习吧! C的指针学习 指针的基本概念 指针的作用:可…...

TPGS-cisplatin顺铂修饰维生素E聚乙二醇1000琥珀酸酯
TPGS-cisplatin顺铂修饰维生素E聚乙二醇1000琥珀酸酯(TPGS)溶于大部分有机溶剂,和水有很好的溶解性。 长期保存需要在-20℃,避光,干燥条件下存放,注意取用一定要干燥,避免频繁的溶解和冻干。 维生素E聚乙二醇琥珀酸酯(简称TPGS)是维生素E的水溶性衍生物,由维生素E…...
【20230206-0209】哈希表小结
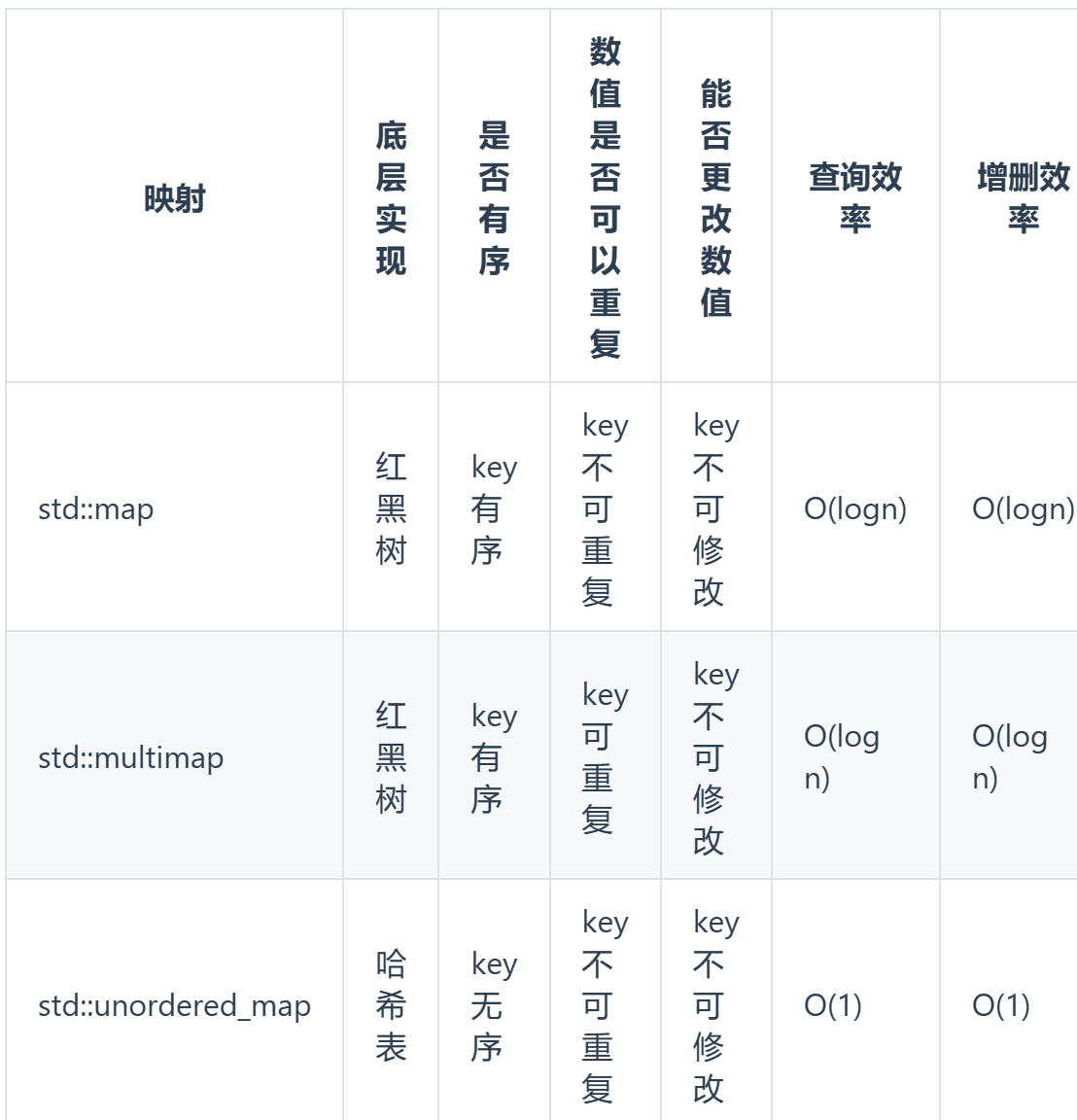
哈希表一般哈希表都是用来快速判断一个元素是否出现在集合里。哈希函数哈希碰撞--解决方法:拉链法和线性探测法。拉链法:冲突的元素都被存储在链表中线性探测法:一定要保证tableSize大于dataSize,利用哈希表中的空位解决碰撞问题。…...
(std::multimap)(一))
c++11 标准模板(STL)(std::multimap)(一)
定义于头文件 <map> template< class Key, class T, class Compare std::less<Key>, class Allocator std::allocator<std::pair<const Key, T> > > class multimap;(1)namespace pmr { template <class Key, class T…...

python进阶——自动驾驶寻找车道
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...
男,26岁,做了一年多的自动化测试,最近在纠结要不要转行,求指点。?
最近一个粉丝在后台问我,啊大佬我现在26了,做了做了一年多的自动化测试,最近在纠结要不要转行,求指点。首选做IT这条路,就是很普通的技术蓝领。对于大部分来说干一辈子问题不大,但是发不了什么财。如果你在…...

源码级别的讲解JAVA 中的CAS
没有CAS之前实现线程安全 多线程环境不使用原子类保证线程安全(基本数据类型) public class T3 {volatile int number 0;//读取public int getNumber(){return number;}//写入加锁保证原子性public synchronized void setNumber(){number;} }多线程环…...

JUC锁与AQS技术【我的Android开发技术】
JUC锁与AQS技术【我的Android开发技术】 AQS原理 AQS就是一个同步器,要做的事情就相当于一个锁,所以就会有两个动作:一个是获取,一个是释放。获取释放的时候该有一个东西来记住他是被用还是没被用,这个东西就是一个状…...

【问题代码】顺序点的深入理解(汇编剖析+手画图解)
这好像是一个哲学问题。 目录 前言 一、顺序点是什么? 二、发生有关顺序点的问题代码 vs中: gcc中: 三、细读汇编 1.vs汇编如下(示例): 2.gcc汇编如下(示例): 四…...
BinaryAI全新代码匹配模型BAI-2.0上线,“大模型”时代的安全实践
导语BinaryAI(https://www.binaryai.net)科恩实验室在2021年8月首次发布二进制安全智能分析平台—BinaryAI,BinaryAI可精准高效识别二进制文件的第三方组件及其版本号,旨在推动SCA(Software Composition Analysis&…...

nvidia设置wifi和接口
tx-nx设置wifi和接口前言基础知识点1.创建和删除一个wifi连接2. 启动连接和关闭连接代码和调试1. 代码展示2. 调试写到最后前言 针对嵌入式开发,有时候通过QT或PAD跨网络对设备设置WIFI,在此记录下,方便后续的查阅。 基础知识点 1.创建和删…...
)
PostgreSQL 变化数据捕捉(CDC)
PostgreSQL 变化数据捕捉(CDC)基于CDC(变更数据捕捉)的增量数据集成总体步骤:1.捕获源数据库中的更改数据2.将变更的数据转换为您的消费者可以接受的格式3.将数据发布到消费者或目标数据库PostgreSQL支持触发器&#x…...

Spring 事务【隔离级别与传播机制】
Spring 事务【隔离级别与传播机制】🍎一.事务隔离级别🍒1.1 事务特性回顾🍒1.2 事务的隔离级别(5种)🍒1.3 事务隔离级别的设置🍎二.Spring 事务传播机制🍒2.1 Spring 事务传播机制的作用🍒2.2 事…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...
