带你了解IP报警柱的特点
IP可视报警柱是一款室外防水紧急求助可视对讲终端。安装在学校、广场、道路人流密集和案件高发区域,当发生紧急情况或需要咨询求助时按下呼叫按钮立即可与监控中心值班人员通话,值班人员也可通过前置摄像头了解现场情况并广播喊话。

IP可视报警柱的使用特点:
1、室外IP55级户外防护能力,防风、防雨、防雷设计;
2、精美外观、安装简易、外观丝印可定制;
3、可独立使用,也可与联网报警平台配套使用;
4、通过Internet网络与联网报警平台连接,当与平台连接时,主机故障了中心平台会有警报提示;
5、全网络化设计,报警迅速,1秒钟内可同时报警到公安局接警值班坐席;
6、面板内置金属防水按钮,按钮常亮提示,户外,夜间都能清晰可见;并具备10万次寿命抗击打和冲击;
7、面板内置高清网络摄像头,支持音视频对讲(可选联动多个摄像机);
8、支持P2P透传,用户无需映射端口可直接配置视频;
9、内置拾音器与喇叭,拾音范围3-5米;
10、高亮度警灯闪烁,指示报警柱位置,报警时发出高分贝警笛声及红光;
11、保密通话,专用音频编码格式,带加密处理;
12、支持平台远程监控、远程喊话;
13、支持远程开启声光警号;
14、传输距离无限延伸,有Internet网络的地方就可以实现对讲;
15、采用动态降噪算法,在各种环境中清晰拾音;
16、先进的数字回声消除技术,全面消除回声,防止啸叫;
17、音质清晰流畅,不受外界电磁波的干扰。
相关文章:

带你了解IP报警柱的特点
IP可视报警柱是一款室外防水紧急求助可视对讲终端。安装在学校、广场、道路人流密集和案件高发区域,当发生紧急情况或需要咨询求助时按下呼叫按钮立即可与监控中心值班人员通话,值班人员也可通过前置摄像头了解现场情况并广播喊话。IP可视报警柱的使用特…...
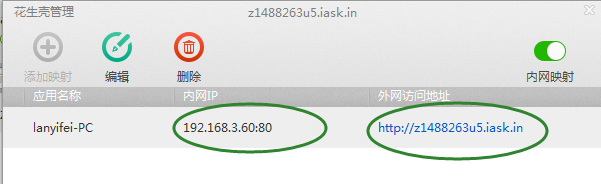
一步步教你电脑变成服务器,tomcat的花生壳设置(原创)
1,首先你去https://console.oray.com/这网站注册个帐号,如果注册成功它会送你一个免费域名,当然不记得也没关系,你记住你注册的 帐号跟密码,然后下载它的软件(花生壳动态域名6.0正式版)有xp跟li…...

Python 卷积神经网络 ResNet的基本编写方法
ResNet(Residual Network)是由微软亚洲研究院提出的深度卷积神经网络,它在2015年的ImageNet挑战赛上取得了第一名的好成绩。ResNet最大的特点是使用了残差学习,可以解决深度网络退化问题。在传统的深度神经网络中,随着…...

【索引】什么是索引
📔 笔记介绍 大家好,千寻简笔记是一套全部开源的企业开发问题记录,毫无保留给个人及企业免费使用,我是作者星辰,笔记内容整理并发布,内容有误请指出,笔记源码已开源,前往Gitee搜索《…...

【算法刷题】动态规划算法题型及方法归纳
动态规划特点 动态规划中每一个状态一定是由上一个状态推导出来,根据这个特点,可以在状态计算过程中,存储某一条件下的数据,当再次遍历该条件时,直接取该条件对应的数据即可,可以避免重复计算,…...

PolarDB数据库的CSN机制
背景 对postgres数据库熟悉的同学会发现在高并发场景下在获取快照处易出现性能瓶颈,其原因在于PG使用全局数组在共享内存中保存所有事务的状态,在获取快照时需要加锁以保证数据一致性。获取快照时需要持有ProcArraryLock共享锁比遍历ProcArray数组中活跃…...

使用kubeadm 部署kubernetes 1.26.1集群 Calico ToR配置
目录 机器信息 升级内核 系统配置 部署容器运行时Containerd 安装crictl客户端命令 配置服务器支持开启ipvs的前提条件 安装 kubeadm、kubelet 和 kubectl 初始化集群 (master) 安装CNI Calico 集群加入node节点 机器信息 主机名集群角色IP内…...
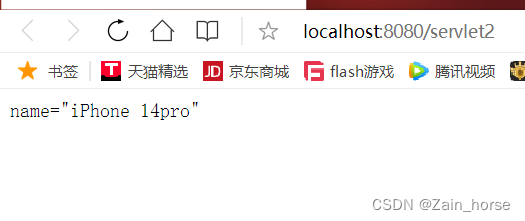
Servlet笔记(11):Servletcontext对象
1、什么是ServletContext ServletContext是一个全局储存空间,随服务器的生命周期变化, Cookie,Session,ServletContext的区别 Cookie: 存在于客户端的本地文本文件 Session: 存在于服务器的文本文件&#…...

EM算法是什么
EM算法是什么 EM算法(Expectation-Maximization Algorithm)是一种用于参数估计的迭代算法。它常被用于含有隐变量(latent variable)的概率模型中,例如高斯混合模型、隐马尔可夫模型等。 EM算法分为两个步骤ÿ…...

C++---线性dp---方格取数(每日一道算法2023.2.25)
注意事项: 本题属于"数字三角形"和"摘花生"两题的进阶版,建议优先看懂那两道,有助理解。 题目: 输入: 8 2 3 13 2 6 6 3 5 7 4 4 14 5 2 21 5 6 4 6 3 15 7 2 14 0 0 0输出: 67#include <cm…...
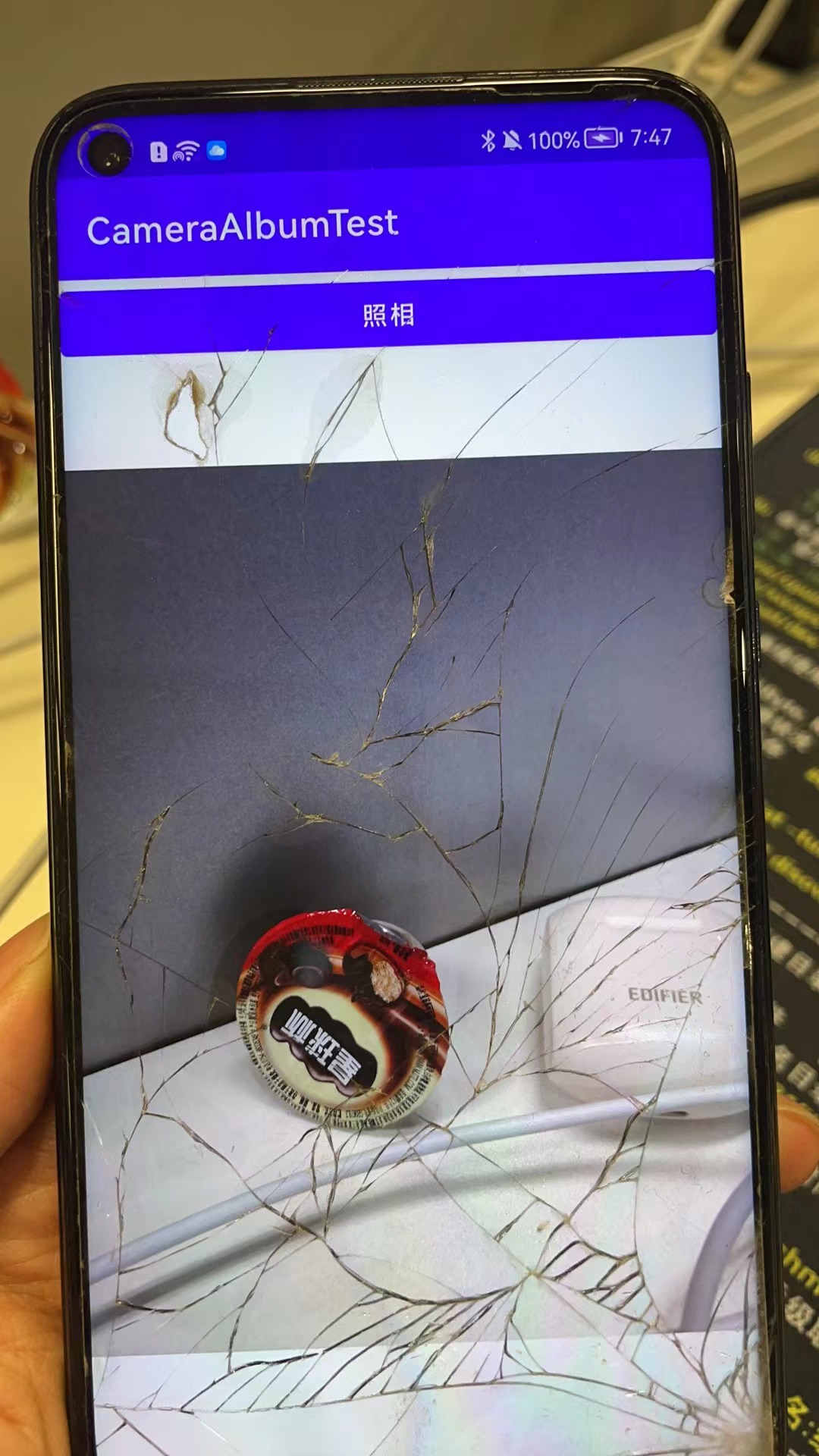
《第一行代码》 第八章:应用手机多媒体
一,使用通知 第一步,创建项目,书写布局 <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"android:orientation"vertical"android:layout_width"match_parent"android:layout_he…...

C++设计模式(20)——迭代器模式
亦称: Iterator 意图 迭代器模式是一种行为设计模式, 让你能在不暴露集合底层表现形式 (列表、 栈和树等) 的情况下遍历集合中所有的元素。 问题 集合是编程中最常使用的数据类型之一。 尽管如此, 集合只是一组对…...
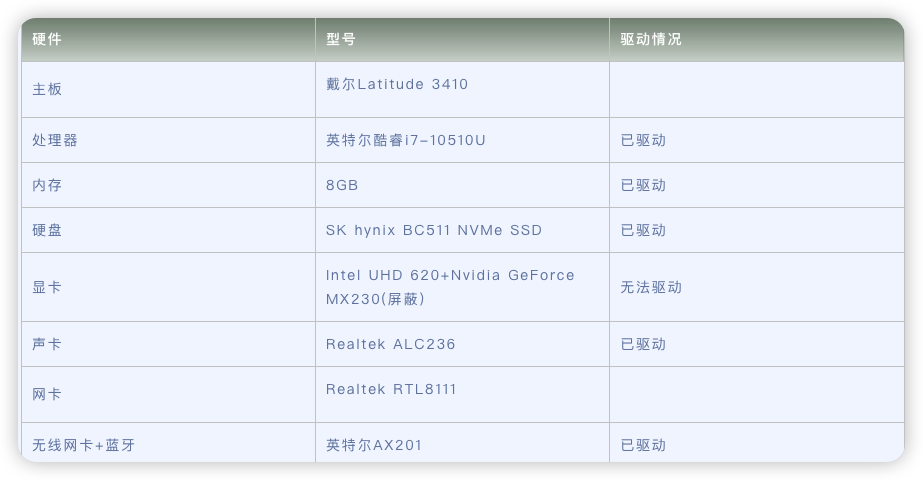
戴尔Latitude 3410电脑 Hackintosh 黑苹果efi引导文件
原文来源于黑果魏叔官网,转载需注明出处。硬件型号驱动情况主板戴尔Latitude 3410处理器英特尔酷睿i7-10510U已驱动内存8GB已驱动硬盘SK hynix BC511 NVMe SSD已驱动显卡Intel UHD 620Nvidia GeForce MX230(屏蔽)无法驱动声卡Realtek ALC236已驱动网卡Realtek RTL81…...
)
一起Talk Android吧(第五百零四回:如何调整组件在约束布局中的位置)
文章目录 背景介绍调整方法一调整方法二经验分享各位看官们大家好,上一回中咱们说的例子是"解决retrofit被混淆后代码出错的问题",这一回中咱们说的例子是" 如何调整组件在约束布局中的位置"。闲话休提,言归正转, 让我们一起Talk Android吧! 背景介绍…...
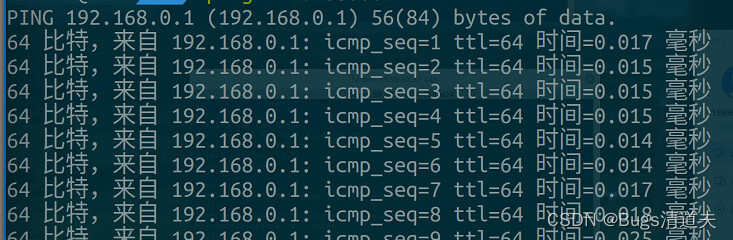
ssh连不上实验室的物理机了
实验室的电脑,不能在校外用 ssh 连接了 192.168.1.33 是本地地址,掩码16位,图1。 192.168.1.14 是实验室的另一台可以ssh连接的物理机,掩码16。 192.168.0.1 是无线路由器地址。 192.168.0.2 是192.168.1.14上的虚拟机地址&#…...

selinux讲解
Selinux讲解 1、selinux的概述 Selinux的历史 Linux安全性与windows在不开启防御措施的时候是一样的;同样是C2级别的安全防护安全级别评定: D–>C1–>C2–>B1–>B2–>B3–>A1 D级,最低安全性C1级,主存取控制…...
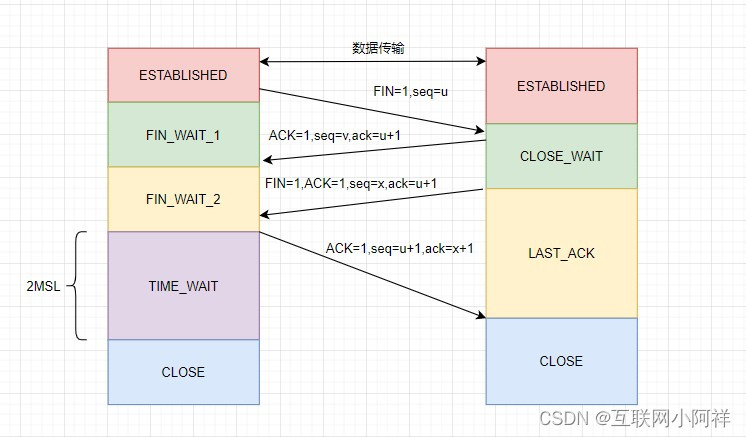
【计算机网络】TCP底层设计交互原理
文章目录1.TCP底层三次握手详细流程2.TCP洪水攻击介绍和ss命令浅析3.Linux服务器TCP洪水攻击入侵案例4.TCP洪水攻击结果分析和解决方案5.TCP底层四次挥手详细流程1.TCP底层三次握手详细流程 TCP的可靠性传输机制:TCP三次我手的流程 一次握手:客户端发送一…...

Kotlin1.8新特性
Kotlin1.8.0新特性 新特性概述 JVM 的新实验性功能:递归复制或删除目录内容提升了 kotlin-reflect 性能新的 -Xdebug 编译器选项,提供更出色的调试体验kotlin-stdlib-jdk7 与 kotlin-stdlib-jdk8 合并为 kotlin-stdlib提升了 Objective-C/Swift 互操作…...
【Java8】
1、接口中默认方法修饰为普通方法 在jdk8之前,interface之中可以定义变量和方法,变量必须是public、static、final的,方法必须是public、abstract的,由于这些修饰符都是默认的。 接口定义方法: public抽象方法需要子类实现 接口定…...

阿里 Java 程序员面试经验分享,附带个人学习笔记、路线大纲
背景经历 当时我工作近5年,明显感觉到了瓶颈期。说句不好听的成了老油条,可以每天舒服的混日子(这也有好处,有时间准备面试)。这对于个人成长不利,长此以往可能面临大龄失业。所以我觉得需要痛下决心改变一…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...
