MATLAB绘制泰勒图(Taylor diagram)
泰勒图(Taylor diagram)
泰勒图是Karl E. Taylor于2001年首先提出,主要用来比较几个气象模式模拟的能力,因此该表示方法在气象领域使用最多,但是在其他自然科学领域也有一定的应用。
泰勒图常用于评价模型的精度,常用的精度指标有相关系数(correlation coefficient),标准差(standard deviation)以及中心均方根误差(centered root-mean-square, RMSE)。
一般而言,泰勒图中的散点代表模型,辐射线代表相关系数,横纵轴代表标准差,而虚线代表均方根误差。泰勒图一改以往用散点图这种只能呈现两个指标来表示模型精度的情况。
泰勒图分为标准化泰勒图和未标准化泰勒图,用的比较多的是标准化泰勒图。标准化泰勒图即对参考值与变量值的标准差与均方根误差同除以参考值的标准差,令参考值=1,E=0,并消除其物理量单位。
泰勒图基本介绍
1 绘制包下载
安装网站:Taylor Diagram
Google Code Archive
此外,还需要"allstats"和"ptable"函数,下载链接分别如下:
Github-allstats.m函数
% STATM Compute statistics from 2 series
%
% STATM = allstats(Cr,Cf)
%
% Compute statistics from 2 series considering Cr as the reference.
%
% Inputs:
% Cr and Cf are of same length and uni-dimensional. They may contain NaNs.
%
% Outputs:
% STATM(1,:) => Mean
% STATM(2,:) => Standard Deviation (scaled by N)
% STATM(3,:) => Centered Root Mean Square Difference (scaled by N)
% STATM(4,:) => Correlation
%
% Notes:
% - N is the number of points where BOTH Cr and Cf are defined
%
% - NaN are handled in the following way: because this function
% aims to compair 2 series, statistics are computed with indices
% where both Cr and Cf are defined.
%
% - STATM(:,1) are from Cr (ie with C=Cr hereafter)
% STATM(:,2) are from Cf versus Cr (ie with C=Cf hereafter)
%
% - The MEAN is computed using the Matlab mean function.
%
% - The STANDARD DEVIATION is computed as:
% / sum[ {C-mean(C)} .^2] \
% STD = sqrt| --------------------- |
% \ N /
%
% - The CENTERED ROOT MEAN SQUARE DIFFERENCE is computed as:
% / sum[ { [C-mean(C)] - [Cr-mean(Cr)] }.^2 ] \
% RMSD = sqrt| ------------------------------------------- |
% \ N /
%
% - The CORRELATION is computed as:
% sum( [C-mean(C)].*[Cr-mean(Cr)] )
% COR = ---------------------------------
% N*STD(C)*STD(Cr)
%
% - STATM(3,1) = 0 and STATM(4,1) = 1 by definition !
%
% Created by Guillaume Maze on 2008-10-28.
% Rev. by Guillaume Maze on 2010-02-10: Add NaN values handling, some checking
% in the inputs and a more complete help
% Copyright (c) 2008 Guillaume Maze.
% http://codes.guillaumemaze.org%
% This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by
% the Free Software Foundation, either version 3 of the License, or any later version.
% This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of
% MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
% You should have received a copy of the GNU General Public License along with this program. If not, see <http://www.gnu.org/licenses/>.
%function STATM = allstats(varargin)Cr = varargin{1}; Cr = Cr(:);
Cf = varargin{2}; Cf = Cf(:);%%% Check size:
if length(Cr) ~= length(Cf)error('Cr and Cf must be of same length');
end%%% Check NaNs:
iok = find(isnan(Cr)==0 & isnan(Cf)==0);
if length(iok) ~= length(Cr)warning('Found NaNs in inputs, removed them to compute statistics');
end
Cr = Cr(iok);
Cf = Cf(iok);
N = length(Cr);%%% STD:
st(1) = sqrt(sum( (Cr-mean(Cr) ).^2) / N );
st(2) = sqrt(sum( (Cf-mean(Cf) ).^2) / N );
%st(1) = sqrt(sum( (Cr-mean(Cr) ).^2) / (N-1) );
%st(2) = sqrt(sum( (Cf-mean(Cf) ).^2) / (N-1) );%%% MEAN:
me(1) = mean(Cr);
me(2) = mean(Cf);%%% RMSD:
rms(1) = sqrt(sum( ( ( Cr-mean(Cr) )-( Cr-mean(Cr) )).^2) /N);
rms(2) = sqrt(sum( ( ( Cf-mean(Cf) )-( Cr-mean(Cr) )).^2) /N);%%% CORRELATIONS:
co(1) = sum( ( ( Cr-mean(Cr) ).*( Cr-mean(Cr) )))/N/st(1)/st(1);
co(2) = sum( ( ( Cf-mean(Cf) ).*( Cr-mean(Cr) )))/N/st(2)/st(1);%%% OUTPUT
STATM(1,:) = me;
STATM(2,:) = st;
STATM(3,:) = rms;
STATM(4,:) = co;end %function
Github-ptable.m函数
ptable.m函数如下:
% PTABLE Creates non uniform subplot handles
%
% SUBPLOT_HANDLE = ptable(TSIZE,PCOORD)
%
% This function creates subplot handles according to
% TSIZE and PCOORD.
% TSIZE(2) is the underlying TABLE of subplots: TSIZE(1)
% is the number of lines, TSIZE(2) the number of rows
% PCOORD(:,2) indicates the coordinates of the subplots, ie
% for each PCOORD(i,2), the subplot i extends from
% initial subplot PCOORD(i,1) to subplot PCOORD(i,2)
%
% Example:
% figure
% subp = ptable([3 4],[1 6 ; 3 4 ; 9 11; 8 8]);
% x = 0:pi/180:2*pi;
% axes(subp(1));plot(x,cos(x));
% axes(subp(2));plot(x,sin(x));
% axes(subp(3));plot(x,sin(x.^2));
% axes(subp(4));plot(x,sin(x).*cos(x));
%
% Copyright (c) 2008 Guillaume Maze.
% http://codes.guillaumemaze.org%
% This program is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by
% the Free Software Foundation, either version 3 of the License, or any later version.
% This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of
% MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
% You should have received a copy of the GNU General Public License along with this program. If not, see <http://www.gnu.org/licenses/>.
%% TO DO:
% - insert input checkfunction varargout = ptable(varargin)tsize = varargin{1}; % [iw jw] of the underlying table
pcoord = varargin{2};%figure
iw = tsize(1);
jw = tsize(2);
tbl = reshape(1:iw*jw,[jw iw])';
for ip = 1 : iw*jwsubp(ip) = subplot(iw,jw,ip);
end% INITIAL POSITIONS:
for ip = 1 : iw*jwposi0(ip,:) = get(subp(ip),'position');
end% HIDE UNNCESSARY PLOTS:
for ip = 1 : iw*jwif isempty(find(pcoord(:,1)==ip))set(subp(ip),'visible','off');
% set(subp(ip),'color','w');else
% set(subp(ip),'color','r');end
end% CHANGE SUBPLOT WIDTH:
for ip = 1 : size(pcoord,1)ip1 = pcoord(ip,1);ip2 = pcoord(ip,2);wi = posi0(ip2,1) + posi0(ip2,3) - posi0(ip1,1);set(subp(ip1),'position',[posi0(ip1,1:2) wi posi0(ip1,4)]);
end% CHANGE SUBPLOT HEIGHT:
for ip = 1 : size(pcoord,1)ip1 = pcoord(ip,1);ip2 = pcoord(ip,2);% Find the lines we are in:[l1 c1] = find(tbl==ip1);[l2 c2] = find(tbl==ip2);% Eventually extent the plot:if l1 ~= l2wi = posi0(ip2,1) + posi0(ip2,3) - posi0(ip1,1);hg = posi0(ip1,2) + posi0(ip1,4) - posi0(ip2,2);bt = posi0(ip2,2);set(subp(ip1),'position',[posi0(ip1,1) bt wi hg]);end
endif nargout >=1varargout(1) = {subp(pcoord(:,1))};
end
1.1 函数说明
markerLabel 图例的名称;markerLegend on为显示图例,off不显示;
styleSTD,sd的线型;colOBS,
| 名称Name | 说明 | – |
|---|---|---|
| ‘tickRMS’ | 坐标刻度范围 | |
| ‘tickSTD’ | 坐标刻度范围 | |
| ‘tickCOR’ | 坐标刻度范围 | |
| markerLabel | 图例的名称 | |
| markerLegend | 图例的名称 | [‘on’/‘off’] |
| styleSTD | sd的线型 | |
| colOBS | 参考点颜色 | ‘r’ |
2 案例
2.1 案例1
结果如下:
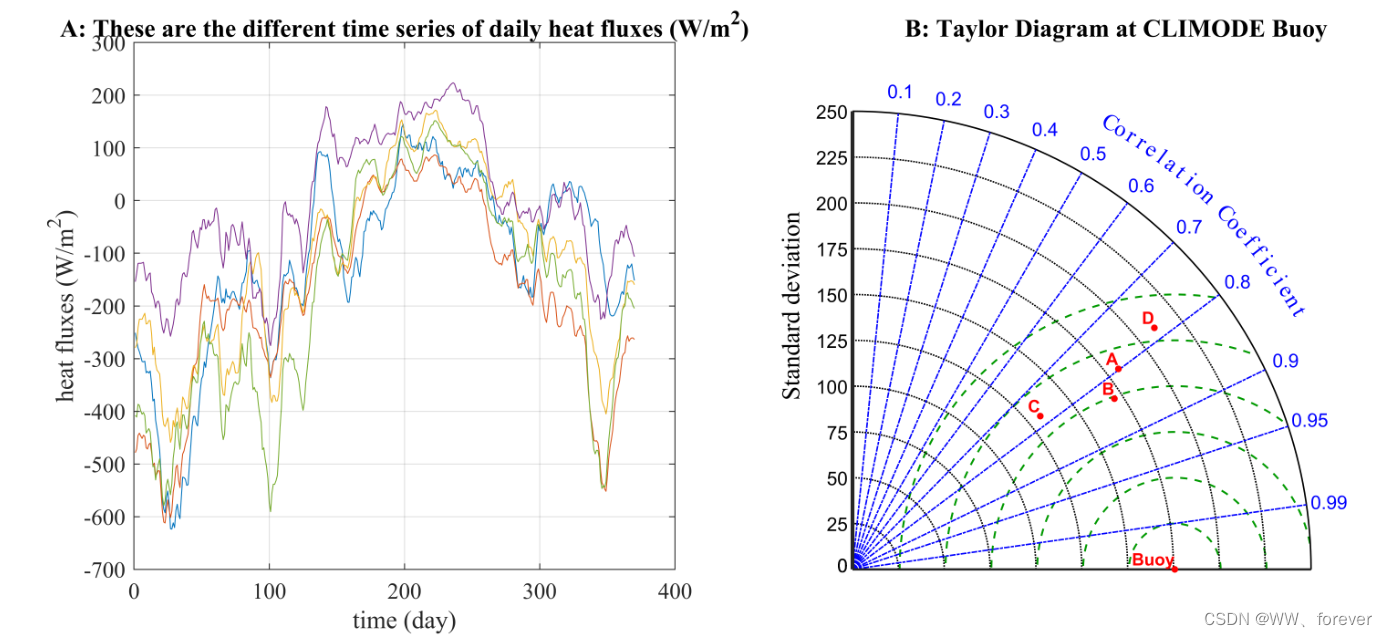
MATLAB代码如下:
clear
%% 导入数据
pathFigure= '.\Figures\' ;
load taylordiag_egdata.mat% Get statistics from time series:
for ii = 2:size(BUOY,1)C = allstats(BUOY(1,:),BUOY(ii,:));statm(ii,:) = C(:,2);
end
statm(1,:) = C(:,1);% Plot:
figureUnits = 'centimeters';
figureWidth = 30;
figureHeight = 12;figure(1)
set(gcf, 'Units', figureUnits, 'Position', [0 0 figureWidth figureHeight]);
ax = ptable([2 3],[2 2;4 6]);
iw=1;
jw=2;
alphab = 'ABCDEFG';subplot(iw,jw,1);
plot(BUOY');
grid on;
xlabel('time (day)','FontSize',12,'FontName','Times New Roman');
ylabel('heat fluxes (W/m^2)','FontSize',12,'FontName','Times New Roman');
title(sprintf('%s: These are the different time series of daily heat fluxes (W/m^2)','A'),'fontweight','bold','FontSize',12,'FontName','Times New Roman');
set(gca,'FontSize',12,'Fontname', 'Times New Roman');
set(gca,'Layer','top');subplot(iw,jw,2);
hold on
[pp tt axl] = taylordiag(squeeze(statm(:,2)),squeeze(statm(:,3)),squeeze(statm(:,4)),...'tickRMS',[25:25:150],'titleRMS',0,'tickRMSangle',135,'showlabelsRMS',0,'widthRMS',1,...'tickSTD',[25:25:250],'limSTD',250,...'tickCOR',[.1:.1:.9 .95 .99],'showlabelsCOR',1,'titleCOR',1);for ii = 1 : length(tt)set(tt(ii),'fontsize',9,'fontweight','bold')set(pp(ii),'markersize',12)if ii == 1set(tt(ii),'String','Buoy');elseset(tt(ii),'String',alphab(ii-1));end
end
title(sprintf('%s: Taylor Diagram at CLIMODE Buoy','B'),'fontweight','bold','FontSize',12,'FontName','Times New Roman');tt = axl(2).handle;
for ii = 1 : length(tt)set(tt(ii),'fontsize',10,'fontweight','normal','FontSize',12,'FontName','Times New Roman');
end
set(axl(1).handle,'fontweight','normal','FontSize',12,'FontName','Times New Roman');
set(gca,'FontSize',12,'Fontname', 'Times New Roman');
set(gca,'Layer','top');str= strcat(pathFigure, "Fig.1", '.tiff');
print(gcf, '-dtiff', '-r600', str);
2.2 案例2
参考
1.CSDN博客-泰勒图(Taylor diagram)
2.CSDN博客-超干货 | 泰勒图(Taylor diagram)绘制方法大汇总
3.MATLAB绘制泰勒图(10个以上model)
相关文章:

MATLAB绘制泰勒图(Taylor diagram)
泰勒图(Taylor diagram) 泰勒图是Karl E. Taylor于2001年首先提出,主要用来比较几个气象模式模拟的能力,因此该表示方法在气象领域使用最多,但是在其他自然科学领域也有一定的应用。 泰勒图常用于评价模型的精度&…...
ClickHouse高可用集群分片-副本实操(四)
目录 一、ClickHouse高可用之ReplicatedMergeTree引擎 二、 ClickHouse高可用架构准备-环境说明和ZK搭建 三、高可用集群架构-ClickHouse副本配置实操 四、ClickHouse高可用集群架构分片 4.1 ClickHouse高可用架构之两分片实操 4.2 ClickHouse高可用架构之两分片建表实操 一…...

2022年中国工业机器人行业市场回顾及2023年发展前景预测分析
工业机器人是一种能自动定位控制、可重复编程的、多功能的、多自由度的操作机,广泛应用于码垛、冲压、分拣、焊接、切割、喷涂、上下料等工业场景中,极大提高了生产效率、安全性以及智能化水平。工业机器人作为我国高端制造业的典型代表,近年…...
Gehpi的网络布局
Gehpi的网络布局1. 力引导布局2. 辅助布局布局是网络可视化中的重要概念,指将点和边通过某种策略进行排布,应尽可能满足以下4个原则: 节点均匀分布在有限的区域内避免边的交叉和弯曲保持边的长度一致整体布局能反映图内在的特性 Gephi的布局…...

华为OD机试用Python实现 -【天然蓄水库 or 天然蓄水池】(2023-Q1 新题)
华为OD机试题 华为OD机试300题大纲天然蓄水库 or 天然蓄水池题目描述输入描述输出描述说明示例一输入输出说明示例二输入输出说明示例三输入输出说明Python 代码实现算法思路华为OD机试300题大纲 参加华为...
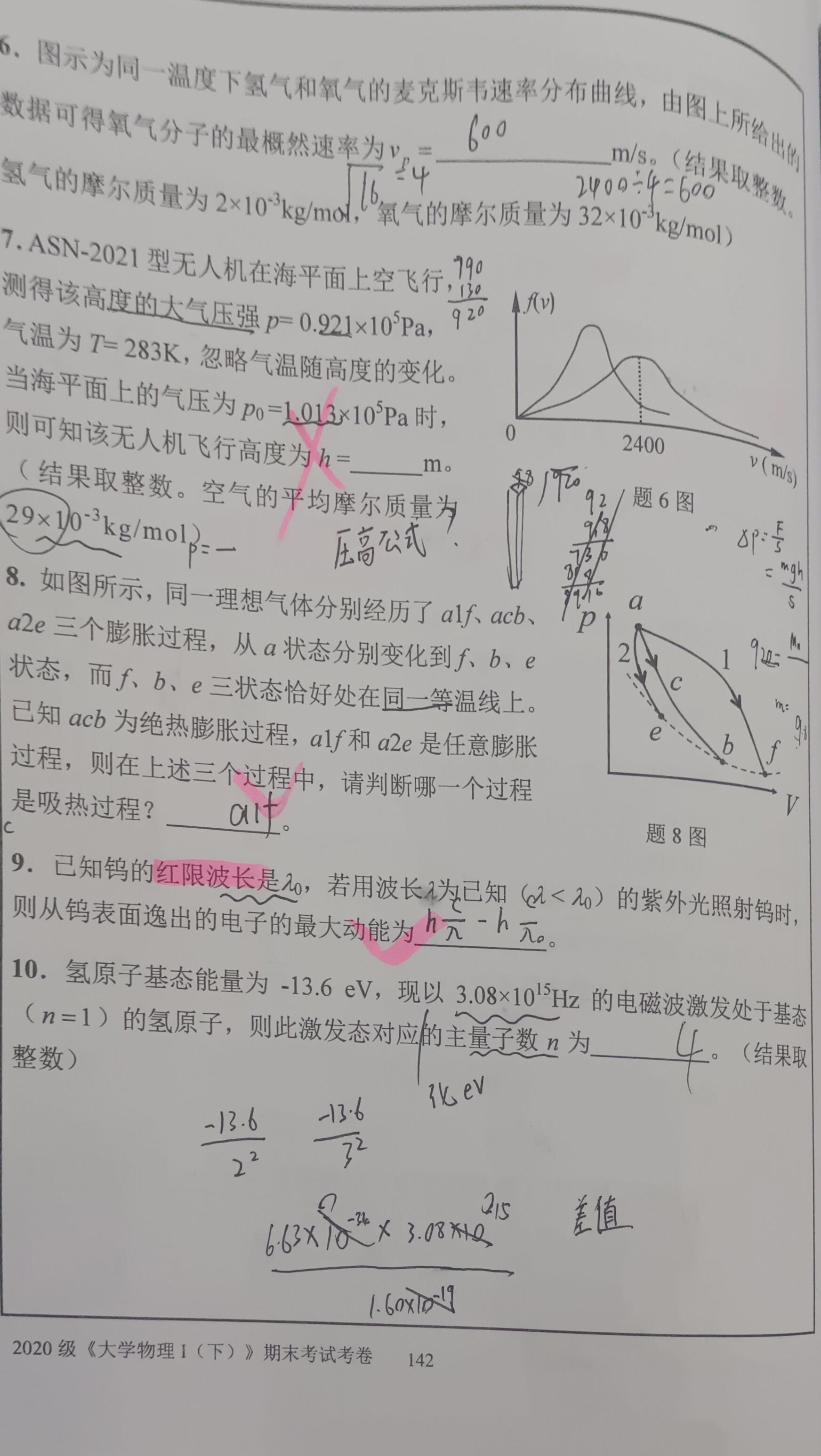
西北工业大学大学物理(I)下期末考试2021-2022选填解析
11 告诉你n2了,那么l0或者1,后续限制类推。2 几乎每年都出。散射波波长的偏移只与散射角有关。3 产生激光的条件。先认识到激光就是受激幅射光放大。受激辐射是产生激光的必要条件,粒子数偏转是产生激光的必要条件,谐振腔也需要。…...

【数据结构】手撕红黑树
目录 一、红黑树简介 1、红黑树的简介 2、红黑树的性质 二、红黑树的插入(看叔叔的颜色就行) 1、为什么新插入的节点必须给红色? 2、插入红色节点后,判定红黑树性质是否被破坏 2.1情况一:uncle存在且为红 2.2情…...

Linux基础命令-which查找命令文件位置
文章目录 which 命令功能 语法格式 基本参数 参考实例 1)查找chmod命令的文件位置 2)查找chmod命令的所有路径 3)一次性查找多个命令路径 4)组合其他命令一起使用 5)显示命令的版本信息 命令总结 which 命…...

在Python中,导入拓展库的规范如下:
在Python中,导入拓展库的规范如下: Import 模块名 [as 别名] from 模块名Import 对象名 [as 别名] from 模块名 import * 1.导入标准库和第三方库的方式应该不同 Python标准库已经默认安装在Python解释器中,因此在导入标准库时不需要…...
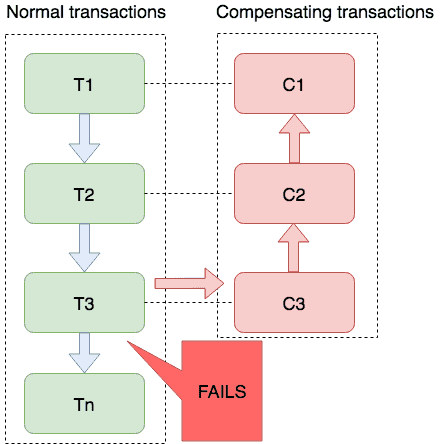
SEATA是什么?它的四种分布式事务模式
一、SEATA是什么? Seata 是一款开源的分布式事务解决方案,致力于提供高性能和简单易用的分布式事务服务。Seata 将为用户提供了 AT、TCC、SAGA 和 XA 事务模式,为用户打造一站式的分布式解决方案。 在继续学习使用SEATA之前,对s…...

【华为OD机试模拟题】用 C++ 实现 - 去重求和(2023.Q1)
最近更新的博客 【华为OD机试模拟题】用 C++ 实现 - 获得完美走位(2023.Q1) 文章目录 最近更新的博客使用说明去重求和题目输入输出示例一输入输出说明示例一输入输出说明Code使用说明 参加华为od机试,一定要注意不要完全背诵代码,需要理解之后模仿写出,通过率才会高。…...

如何用 chatGPT,给大家来一个自我介绍
大家好,我是不吃西红柿的无线机械键盘,我的名字叫 Keychron K3 Pro。今天,我通过西红柿主人的手,使用 chatGPT 来介绍一下我自己。我的与众不同 我是由精密机械元件制作而成,并采用抗键渗设计,以提供更快、…...
进程管理之基本概念
目录 关于进程的基本概念 进程描述符 查看进程 进程标识 进程的生命周期 僵尸进程、孤儿进程 写时拷贝技术 fork()函数 vfork()函数 终止进程 进程优先级和权重 进程地址空间 关于进程的基本概念 进程和程序是操作系统领域的两个重要的概念,进程是执行…...
nginx安装部署实战手册
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录一、虚拟机安装nginx1.下载安装包2.安装编译工具和库文件3.编译安装4.启动nginx5.访问首页6.开机自启结尾一、虚拟机安装nginx 1.下载安装包 官网下载地址…...

XXL-JOB任务调度平台
什么是xxl-job? xxl-job是一个分布式的任务调度平台,其核心设计目标是:学习简单、开发迅速、轻量级、易扩展,现在已经开放源代码并接入多家公司的线上产品线,开箱即用。xxl是xxl-job的开发者大众点评的许雪里名称的拼…...

android UI优化的基本原理和实战方法
任何Android应用都需要UI跟用户交互.UI是否好坏更是直接影响到用户的体验.如今UI的优化视乎是应用开发中一个绕不过去的话题。所以本篇文章小编带大家全面了解Android ui优化的主要知识和优化方法。 一、UI优化 UI优化知识点主要分为三部分: 第一部分,…...

指针的进阶【中篇】
文章目录📀4.数组参数💿4.1.一维数组传参💿4.2.二维数组传参📀5.指针参数💿5.1.一级指针传参💿5.2.二级指针传参📀6.函数指针💿6.1. 代码1💿6.2. 代码2📀7.函…...

华为OD机试题,用 Java 解【删除字符串中出现次数最少的字符】问题
最近更新的博客 华为OD机试 - 猴子爬山 | 机试题算法思路 【2023】华为OD机试 - 分糖果(Java) | 机试题算法思路 【2023】华为OD机试 - 非严格递增连续数字序列 | 机试题算法思路 【2023】华为OD机试 - 消消乐游戏(Java) | 机试题算法思路 【2023】华为OD机试 - 组成最大数…...

【C语言每日一题】猜名次
【C语言每日一题】—— 猜名次😎😎😎 💡前言🌞: 💛猜名次题目💛 💪 解题思路的分享💪 😊题目源码的分享😊 👉 本菜鸡…...

89. 格雷编码
89. 格雷编码题目数学公式动态规划回溯题目 传送门:https://leetcode.cn/problems/gray-code/ 数学公式 int gray(int n) { // 计算第n位格雷码公式return n ^ (n >> 1); }然后你写一个for循环,计算从1到n的所有格雷码,添加到答…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...
