【深度学习】吴恩达课程笔记(二)——浅层神经网络、深层神经网络
笔记为自我总结整理的学习笔记,若有错误欢迎指出哟~
笔记链接
【深度学习】吴恩达课程笔记(一)——深度学习概论、神经网络基础
吴恩达课程笔记——浅层神经网络、深层神经网络
- 四、浅层神经网络
- 1.双层神经网络表示
- 2.双层神经网络的前向传播
- 第一层前向传播
- 第二层前向传播
- 3.双层神经网络的反向传播
- 参数
- 梯度下降
- 反向传播公式
- 第二层反向传播推导
- 4.激活函数
- 5.为什么要使用非线性激活函数?
- 6.为什么要对W随机初始化?
- 五、深层神经网络
- 1.变量定义
- 2.矩阵的维数
- 3.为什么使用深层表示(Deep Representation)
- 4.深层神经网络块图解
- 5.深层神经网络前向和反向传播的实现
四、浅层神经网络
1.双层神经网络表示


x1 ,x2 ,x3:输入层A[0],指的是单个样本的输入值
中间四个神经元:隐藏层A[1]
右侧的单个神经元:输出层A[2]
单次训练过程:
-
正向传播
- 训练样本分别对隐藏层的各神经元的参数(w向量和b值)进行计算得到z[1]
- 各神经元的z放到一起组成Z[1]
- z[1]激活后得到a
- 各神经元的a放到一起组成A[1]
z 1 [ 1 ] = w 1 [ 1 ] T x + b 1 [ 1 ] , a 1 [ 1 ] = σ ( z 1 [ 1 ] ) z 2 [ 1 ] = w 2 [ 1 ] T x + b 2 [ 1 ] , a 1 [ 1 ] = σ ( z 2 [ 1 ] ) z 3 [ 1 ] = w 3 [ 1 ] T x + b 3 [ 2 ] , a 1 [ 1 ] = σ ( z 3 [ 1 ] ) z 4 [ 1 ] = w 4 [ 1 ] T x + b 4 [ 1 ] , a 1 [ 1 ] = σ ( z 4 [ 1 ] ) z^{[1]}_{1}=w^{[1]T}_{1}x+b^{[1]}_{1},a^{[1]}_{1}=σ(z^{[1]}_{1})\\ z^{[1]}_{2}=w^{[1]T}_{2}x+b^{[1]}_{2},a^{[1]}_{1}=σ(z^{[1]}_{2})\\ z^{[1]}_{3}=w^{[1]T}_{3}x+b^{[2]}_{3},a^{[1]}_{1}=σ(z^{[1]}_{3})\\ z^{[1]}_{4}=w^{[1]T}_{4}x+b^{[1]}_{4},a^{[1]}_{1}=σ(z^{[1]}_{4})\\ z1[1]=w1[1]Tx+b1[1],a1[1]=σ(z1[1])z2[1]=w2[1]Tx+b2[1],a1[1]=σ(z2[1])z3[1]=w3[1]Tx+b3[2],a1[1]=σ(z3[1])z4[1]=w4[1]Tx+b4[1],a1[1]=σ(z4[1])

- 各神经元的A[1]再作为训练样本对对输出层的单个神经元的参数(w向量和b值)进行计算得到z[2]
- z[2]激活得到a[2]
Z [ 1 ] = W [ 1 ] X + b [ 1 ] A [ 1 ] = σ ( Z [ 1 ] ) Z [ 2 ] = W [ 2 ] A [ 1 ] + b [ 2 ] A [ 2 ] = σ ( Z [ 2 ] ) Z^{[1]}=W^{[1]}X+b^{[1]}\\ A^{[1]}=σ(Z^{[1]})\\ Z^{[2]}=W^{[2]}A^{[1]}+b^{[2]}\\ A^{[2]}=σ(Z^{[2]}) Z[1]=W[1]X+b[1]A[1]=σ(Z[1])Z[2]=W[2]A[1]+b[2]A[2]=σ(Z[2])
-
反向传播
- 从输出结果到第二层到第一层依次计算对成本函数的导数,达到对各个w、b的迭代、训练效果
2.双层神经网络的前向传播
多个样本
训练样本集:X = [x(1),x(2),x(3), … ,x(m)],其中x(i)是第 i 个训练样本,共m个样本
n[0]:第n层的单元数,n[0]表示特征向量x的维度
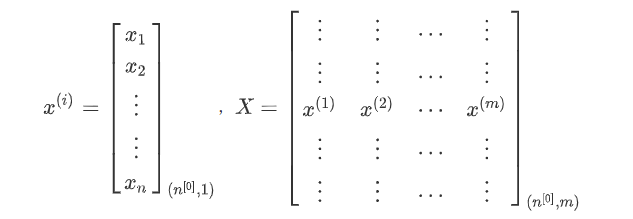
第一层前向传播
第一层神经元的w参数集:

第一层神经元的b参数集:
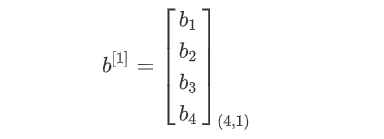
第一层前向传播过程计算Z[1]
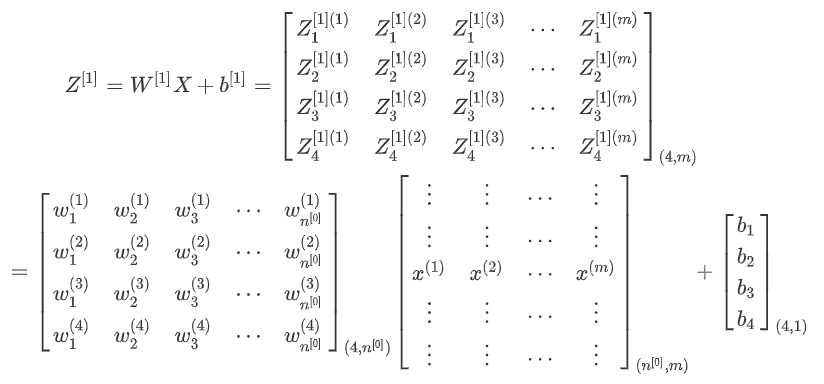
第一层前向传播过程计算A[1]
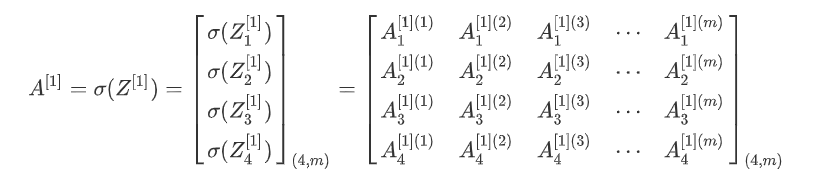
第二层前向传播
第二层神经元的w参数集:
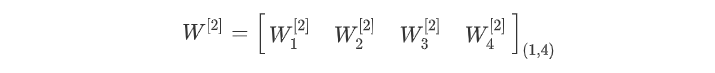
第二层神经元的b参数集:
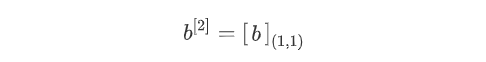
第二层前向传播过程计算Z[2]

第二层前向传播过程计算A[2]
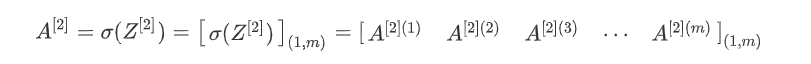
核对矩阵维数
第一层 X . s h a p e = ( n [ 0 ] , m ) W [ 1 ] . s h a p e = ( n [ 1 ] , n [ 0 ] ) b [ 1 ] . s h a p e = ( n [ 1 ] , 1 ) Z [ 1 ] . s h a p e = ( n [ 1 ] , m ) A [ 1 ] . s h a p e = ( n [ 1 ] , m ) 第二层 W [ 2 ] . s h a p e = ( n [ 2 ] , n [ 1 ] ) Z [ 2 ] . s h a p e = ( n [ 2 ] , m ) A [ 2 ] . s h a p e = ( n [ 2 ] , m ) Y . s h a p e = A [ 2 ] . s h a p e = ( n [ 2 ] , m ) \textcolor{red}{第一层}\\ X.shape=(n^{[0]},m)\\ W^{[1]}.shape=(n^{[1]},n^{[0]})\\ b^{[1]}.shape=(n^{[1]},1)\\ Z^{[1]}.shape=(n^{[1]},m)\\ A^{[1]}.shape=(n^{[1]},m)\\ \textcolor{red}{第二层} \\ W^{[2]}.shape=(n^{[2]},n^{[1]})\\ Z^{[2]}.shape=(n^{[2]},m)\\ A^{[2]}.shape=(n^{[2]},m)\\ Y.shape=A^{[2]}.shape=(n^{[2]},m) 第一层X.shape=(n[0],m)W[1].shape=(n[1],n[0])b[1].shape=(n[1],1)Z[1].shape=(n[1],m)A[1].shape=(n[1],m)第二层W[2].shape=(n[2],n[1])Z[2].shape=(n[2],m)A[2].shape=(n[2],m)Y.shape=A[2].shape=(n[2],m)
3.双层神经网络的反向传播
参数
训练样本维数: n [ 0 ] 隐藏层神经元个数: n [ 1 ] 输出层神经元个数: n [ 2 ] = 1 W [ 1 ] : ( n [ 1 ] , n [ 0 ] ) b [ 1 ] : ( n [ 1 ] , 1 ) W [ 2 ] : ( n [ 2 ] , n [ 1 ] ) b [ 2 ] : ( n [ 2 ] , 1 ) 成本函数: J ( W , b ) = 1 m ∑ i = 1 m L ( y ^ i , y i ) 训练样本维数:n^{[0]} \\ 隐藏层神经元个数:n^{[1]} \\ 输出层神经元个数:n^{[2]}=1 \\ W^{[1]}:(n^{[1]},n^{[0]})\\ b^{[1]}:(n^{[1]},1)\\ W^{[2]}:(n^{[2]},n^{[1]})\\ b^{[2]}:(n^{[2]},1)\\ 成本函数:J(W,b)=\frac{1}{m}\sum_{i=1}^{m}{L(ŷ_i,y_i)} 训练样本维数:n[0]隐藏层神经元个数:n[1]输出层神经元个数:n[2]=1W[1]:(n[1],n[0])b[1]:(n[1],1)W[2]:(n[2],n[1])b[2]:(n[2],1)成本函数:J(W,b)=m1i=1∑mL(y^i,yi)
梯度下降
d W [ i ] = ∂ J ∂ W [ i ] , d b [ i ] = ∂ J ∂ b [ i ] W [ i ] = W [ i ] − α d W [ i ] b [ i ] = b [ i ] − α d b [ i ] i = 1 , 2 dW^{[i]}=\frac{\partial J}{\partial W^{[i]}},db^{[i]}=\frac{\partial J}{\partial b^{[i]}}\\ W^{[i]}=W^{[i]}-\alpha dW{[i]} \\ b^{[i]}=b^{[i]}-\alpha db{[i]}\\ i=1,2 dW[i]=∂W[i]∂J,db[i]=∂b[i]∂JW[i]=W[i]−αdW[i]b[i]=b[i]−αdb[i]i=1,2
反向传播公式
d Z [ 2 ] = A [ 2 ] − Y d W [ 2 ] = 1 m d Z [ 2 ] A [ 1 ] T d b [ 2 ] = 1 m n p . s u m ( d Z [ 2 ] , a x i s = 1 , k e e p d i m s = T r u e ) d Z [ 1 ] = W [ 2 ] T d Z [ 1 ] ∗ g [ 1 ] ′ ( Z [ 1 ] ) d W [ 1 ] = 1 m d Z [ 1 ] X T d b [ 1 ] = 1 m n p . s u m ( d Z [ 1 ] , a x i s = 1 , k e e p d i m s = T r u e ) dZ^{[2]}=A^{[2]}-Y\\ dW^{[2]}=\frac{1}{m}dZ^{[2]}A^{[1]T}\\ db^{[2]}=\frac{1}{m}np.sum(dZ^{[2]},axis=1,keepdims=True)\\ dZ^{[1]}=W^{[2]T}dZ^{[1]}*g^{[1]'}(Z^{[1]})\\ dW^{[1]}=\frac{1}{m}dZ^{[1]}X^{T}\\ db^{[1]}=\frac{1}{m}np.sum(dZ^{[1]},axis=1,keepdims=True)\\ dZ[2]=A[2]−YdW[2]=m1dZ[2]A[1]Tdb[2]=m1np.sum(dZ[2],axis=1,keepdims=True)dZ[1]=W[2]TdZ[1]∗g[1]′(Z[1])dW[1]=m1dZ[1]XTdb[1]=m1np.sum(dZ[1],axis=1,keepdims=True)
第二层反向传播推导

4.激活函数
-
sigmoid:只可能用于二元分类的输出层。
a = 1 1 + e − z d a d z = a ( 1 − a ) a=\frac{1}{1+e^{-z}}\\ \frac{da}{dz}=a(1-a) a=1+e−z1dzda=a(1−a)

-
tanh:几乎在所有情况下优于sigmoid函数。(计算速度更快)
a = e z − e − z e z + e − z d a d z = 1 − a 2 a=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}\\ \frac{da}{dz}=1-a^2 a=ez+e−zez−e−zdzda=1−a2

-
ReLU(Rectified Linear Unit):最常用的默认激活函数
a = m a x ( 0 , z ) d a d z = { 0 , z < 0 1 , z > 0 u n d e f i n e d , z = 0 a=max(0,z)\\ \frac{da}{dz}=\left\{ \begin{aligned} 0 & , z<0 \\ 1 & , z>0 \\ undefined&,z=0 \end{aligned} \right. a=max(0,z)dzda=⎩ ⎨ ⎧01undefined,z<0,z>0,z=0

-
leaky ReLU:有人认为这个比ReLU好
a = m a x ( α z , z ) , α u s u a l l y l e s s t h a n 1 d a d z = { α , z < 0 1 , z > 0 u n d e f i n e d , z = 0 a=max(\alpha z,z),\alpha \ usually \ less\ than\ 1\\ \frac{da}{dz}=\left\{ \begin{aligned} \alpha & , z<0 \\ 1 & , z>0 \\ undefined&,z=0 \end{aligned} \right. a=max(αz,z),α usually less than 1dzda=⎩ ⎨ ⎧α1undefined,z<0,z>0,z=0

5.为什么要使用非线性激活函数?
- 解决线性不可分问题:线性激活函数(如恒等映射)只能产生线性变换,无法处理非线性可分的问题。
- 增强模型的表达能力:非线性激活函数能够引入非线性变换,使得神经网络能够学习更加复杂的模式和特征。
- 防止梯度消失:在深层神经网络中,使用线性激活函数会导致梯度逐层地缩小,进而导致梯度消失的问题。
- 增加模型的非线性响应:非线性激活函数可以引入非线性响应,使得模型能够更好地适应数据的非线性特征。这对于处理图像、语音等复杂数据具有重要意义,能够提高模型的性能。
只有一种情况可能使用线性激活函数:在输出层。
6.为什么要对W随机初始化?
- 如果把W初始化为全部为0,那么第一层上的神经元训练后都将是相同的,其下一层的神经元对上一层的判断权重也是完全相同的,同时这一层的神经元也会是完全相同的。由归纳法,每一层上的神经元都是完全相同的。这样就丧失了多层神经网络的判断性能优势。
- 初始化时应该使W中的数字尽量小,以使得sigmoid或tanh计算导数时处于导数较大的区域,以保证迭代学习的速度
五、深层神经网络
1.变量定义
| 变量名 | 变量含义 |
|---|---|
| l | 层数 |
| n[l] | l 层的单元数 |

2.矩阵的维数
| 矩阵符号 | 矩阵维数 |
|---|---|
| X | (n[0],m) |
| W[l] and dW[l] | (n[l],n[l-1]) |
| b[l] and db[l] | (n[l],1) |
| Z[l] and dZ[l] | (n[l],m) |
| A[l] and dA[l] | (n[l],m) |
| Y | (n[the last l ],m) |
3.为什么使用深层表示(Deep Representation)
深层表示(Deep Representation)是神经网络中的一个重要概念,它指的是通过多层非线性变换来逐步提取输入数据的高级特征表示。
以下是使用深层表示的几个主要原因:
- 特征表达能力增强:深层表示可以通过逐层的非线性变换,将原始输入数据转化为更高级别的抽象特征表示。每一层都可以学习到数据的不同抽象层次的特征,使得模型能够更好地捕捉输入数据中的结构和模式。相比于浅层模型,深层表示具有更强大的特征表达能力。
- 特征的层次化表示:深层表示可以将输入数据的特征表示分解为多个层次,每一层都对应着不同抽象层次的特征。这种层次化的特征表示使得模型能够更好地理解数据的结构和语义,从而提高模型的泛化能力和鲁棒性。
- 梯度传播更有效:在深层网络中,通过反向传播算法计算梯度时,梯度可以更容易地传播到较早的层。这是因为深层网络中的参数共享和权重共享的结构,使得梯度能够通过多个层级的连接路径传递。相比于浅层网络,深层网络可以更有效地利用梯度信息进行参数更新,从而提高模型的训练效率和性能。
- 数据表示的可分离性:深层表示可以将输入数据的不同方面进行分离和表示。例如,在图像处理任务中,底层的卷积层可以学习到边缘和纹理等低级特征,而高层的全连接层可以学习到物体的形状和类别等高级特征。这种分离性使得模型能够更好地对不同方面的特征进行建模和学习。
4.深层神经网络块图解


5.深层神经网络前向和反向传播的实现
前向传播
A [ 0 ] = X Z [ l ] = W [ 1 ] A [ l − 1 ] + b [ l ] A [ l ] = g [ l ] ( Z [ l ] ) A^{[0]}=X\\ Z^{[l]}=W^{[1]}A^{[l-1]}+b^{[l]}\\ A^{[l]}=g^{[l]}(Z^{[l]})\\ A[0]=XZ[l]=W[1]A[l−1]+b[l]A[l]=g[l](Z[l])
反向传播
d Z [ l ] = d A [ l ] ∗ g [ l ] ′ ( Z [ l ] ) d W [ l ] = 1 m d Z [ l ] A [ l − 1 ] T d b [ l ] = 1 m n p . s u m ( d Z [ l ] , a x i s = 1 , k e e p d i m s = T r u e ) d A [ l − 1 ] = W [ l ] T d Z [ l ] \textcolor{red}{}\\ dZ^{[l]}=dA^{[l]}*g^{[l]'}(Z^{[l]})\\ dW^{[l]}=\frac{1}{m}dZ^{[l]}A^{[l-1]T}\\ db^{[l]}=\frac{1}{m}np.sum(dZ^{[l]},axis=1,keepdims=True)\\ dA^{[l-1]}=W^{[l]T}dZ^{[l]} dZ[l]=dA[l]∗g[l]′(Z[l])dW[l]=m1dZ[l]A[l−1]Tdb[l]=m1np.sum(dZ[l],axis=1,keepdims=True)dA[l−1]=W[l]TdZ[l]
相关文章:

【深度学习】吴恩达课程笔记(二)——浅层神经网络、深层神经网络
笔记为自我总结整理的学习笔记,若有错误欢迎指出哟~ 笔记链接 【深度学习】吴恩达课程笔记(一)——深度学习概论、神经网络基础 吴恩达课程笔记——浅层神经网络、深层神经网络 四、浅层神经网络1.双层神经网络表示2.双层神经网络的前向传播第一层前向传播第二层前…...

UI自动化概念 + Web自动化测试框架介绍
1.UI自动化测试概念:我们先明确什么是UI UI,即(User Interface简称UI用户界面)是系统和用户之间进行交互和信息交换的媒介 UI自动化测试: Web自动化测试和移动自动化测试都属于UI自动化测试,UI自动化测试就是借助自动化工具对程序UI层进行自动化的测试 …...

在 macOS 上的多个 PHP 版本之间切换
文章目录 前言一、前提条件1.引入库需要安装 Xcode 2.安装多个PHP版本2.PHP版本切换 开源替代品 前言 不同项目使用php版本可能不同,需要安装不同版本php 一、前提条件 1.引入库 需要安装 Xcode 命令行工具和Homebrew xcode-select --install检查brew是否已安…...

地址解析协议ARP
地址解析协议(Address Resolution Protocol,ARP),用于根据本网内目的主机或默认网关的IP地址获取其MAC地址。 ARP的基本思想:在每一台主机中设置专用内存区域,称为ARP高速缓存(也称为ARP表&…...

Go学习第十三章——Gin入门与路由
Go web框架——Gin入门与路由 1 Gin框架介绍1.1 基础介绍1.2 安装Gin1.3 快速使用 2 路由2.1 基本路由GET请求POST请求 2.2 路由参数2.3 路由分组基本分组带中间件的分组 2.4 重定向 1 Gin框架介绍 github链接:https://github.com/gin-gonic/gin 中文文档…...

[减脂期食谱] 自制千岛酱
[减脂期食谱] 自制千岛酱 成品如下: 最中间的那个,算比较居中的颜色吧,其实自己家做原版的千岛酱还是比较简单的,它的底就是蛋黄酱(蛋黄油乳化的酱),随后里面的材料比较自由,维基百科是这么介绍的…...

Android 系统架构
目录 Android 系统架构 1. Android 应用层 2. Android应用框架层 2.1 Activity Manager (活动管理器) 2.2 Window Manager (窗口管理器) 2.3 Content Provider (内容提供器) 2.4 View System(视图系统&a…...

【Docker】Python Flask + Redis 练习
一、构建flask镜像 1.准备文件 创建app.py,内容如下 from flask import Flask from redis import Redis app Flask(__name__) redis Redis(hostos.environ.get(REDIS_HOST,127.0.0.1),port6379)app.route(/) def hello():redis.incr(hits)return f"Hello Container W…...

shell_52.Linux测试与其他网络主机的连通性脚本
实战演练 本节将展示一个实用脚本,该脚本在处理用户输入的同时,使用 ping 命令或 ping6 命令来测试与其他网络主机的连通性。 ping 命令或 ping6 命令可以快速测试网络主机是否可用。这个命令很有用,经常作为首选工具。如果只是检查单个主机&…...
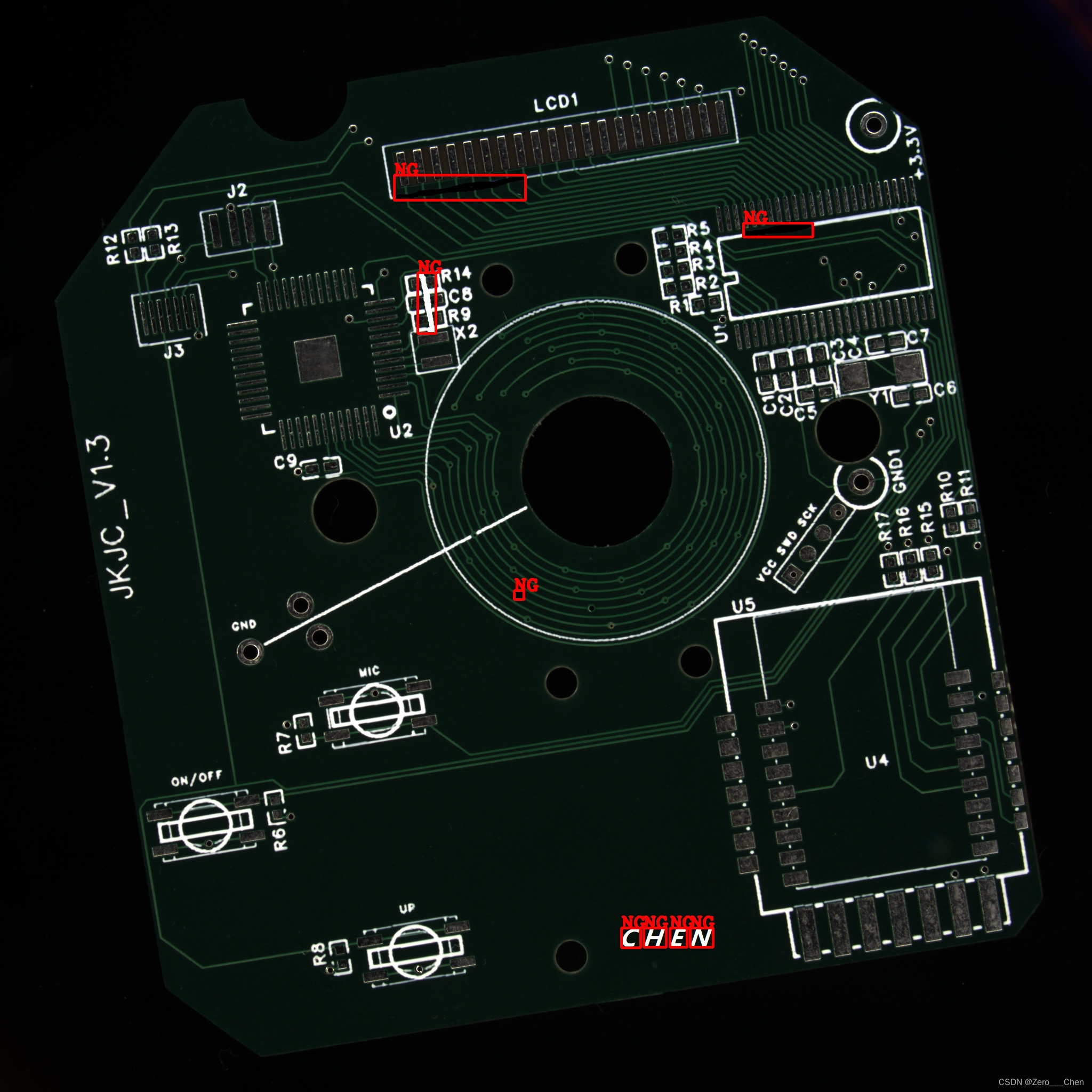
OpenCV C++ 图像处理实战 ——《缺陷检测》
OpenCV C++ 图像处理实战 ——《缺陷检测》 一、结果演示二、缺陷检测算法2.1、多元模板图像2.2、训练差异模型三、图像配准3.1 功能源码3.1 功能效果四、多元模板图像4.1 功能源码五、缺陷检测5.1 功能源码六、源码测试图像下载总结一、结果演示...

Python操作MySQL基础使用
Python操作MySQL基础使用 链接数据库并查询数据 import pymysql# 链接数据库 conn pymysql.connect(host10.5.6.250,port3306,userroot,password******** )# 查看MySQL版本信息 print(conn.get_server_info()) # 5.5.27# 获取到游标对象 cursor conn.cursor()# 选择数据库…...

【pytorch】pytorch中的高级索引
这里只介绍pytorch的高级索引,是一些奇怪的切片索引 基本版 a[[0, 2], [1, 2]] 等价 a[0, 1] 和 a[2, 2],相当于索引张量的第一行的第二列和第三行的第三列元素; a[[1, 0, 2], [0]] 等价 a[1, 0] 和 a[0, 0] 和 a[2, 0],相当于索…...

基于图像识别的自动驾驶汽车障碍物检测与避障算法研究
基于图像识别的自动驾驶汽车障碍物检测与避障算法研究是一个涉及计算机视觉、机器学习、人工智能和自动控制等多个领域的复杂问题。以下是对这个问题的研究内容和方向的一些概述。 障碍物检测 障碍物检测是自动驾驶汽车避障算法的核心部分,它需要从车辆的感知数据…...

Spring boot定时任务
目录 前言一、使用 Scheduled 注解二、使用 ScheduledExecutorService三、使用 Spring 的 TaskScheduler四、使用第三方调度框架 前言 在 Spring Boot 中,有多种方法来编写定时任务,以执行周期性或延迟执行的任务。下面是几种常见的方式 一、使用 Sche…...
Glide原理
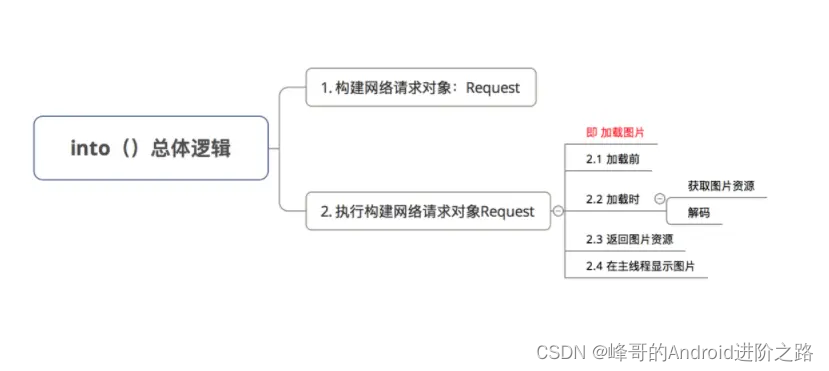
本文基于Carson整理 1.简介 相比其他几种图片加载框架,Glide性能最好。这得益于其高效的图片缓存策略 其还有多样化的媒体格式加载:如GIF、Video,对于商城首页需展示丰富样式、信息的页面需求来说,也是必不可少的。 2.加载原理…...
wps表格按分隔符拆分单元格
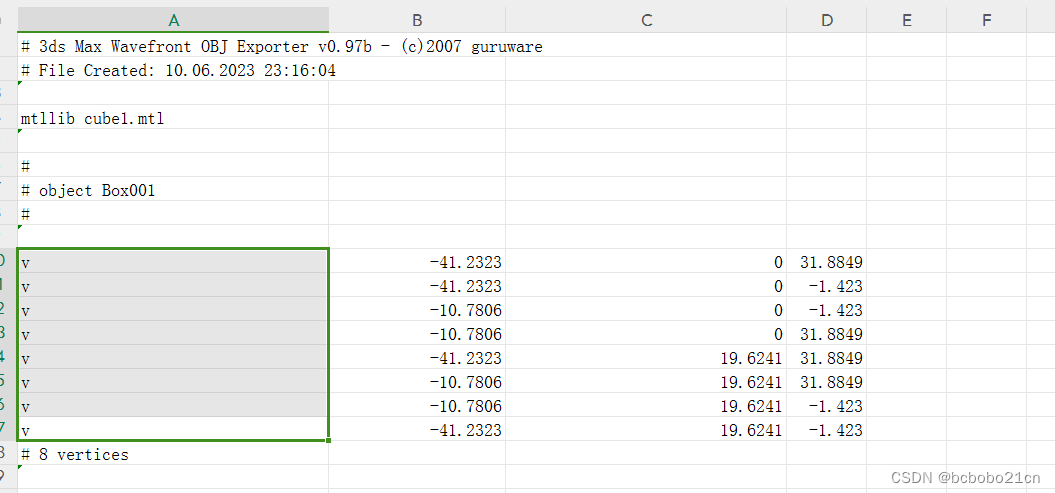
有数据如下;看选中区域,一个单元格中有一个v,空格,然后有三个数值,以空格分开;点击菜单中的数据-分列; 弹出分列向导;选择 分隔符号; 选择分隔符为空格;出现预…...

【SEC 学习】Vim 的基本使用
一、Vim 编辑器安装 yum install -y vim二、Vim 三种模式 命令模式 编辑模式 末行模式 三、三种模式之间的转换 1. 命令模式 -> 编辑模式 快捷键含义i从光标处插入I从光标所在行首插入a从光标后插入A从光标所在行末插入o从光标下一行插入O从光标上一行插入 2. 命令模式 …...
Linux中shell脚本练习
目录 1.猜数字 2.批量创建用户 3.监控网卡Receive Transmit 数据的变化 4.部署Linux 5.系统性能检测脚本 6.分区脚本 7.数据库脚本 1.猜数字 随机数的生成 使用环境变量RANDOM,范围是0~32767 编写guest.sh,实现以下功能࿱…...
AS/400简介
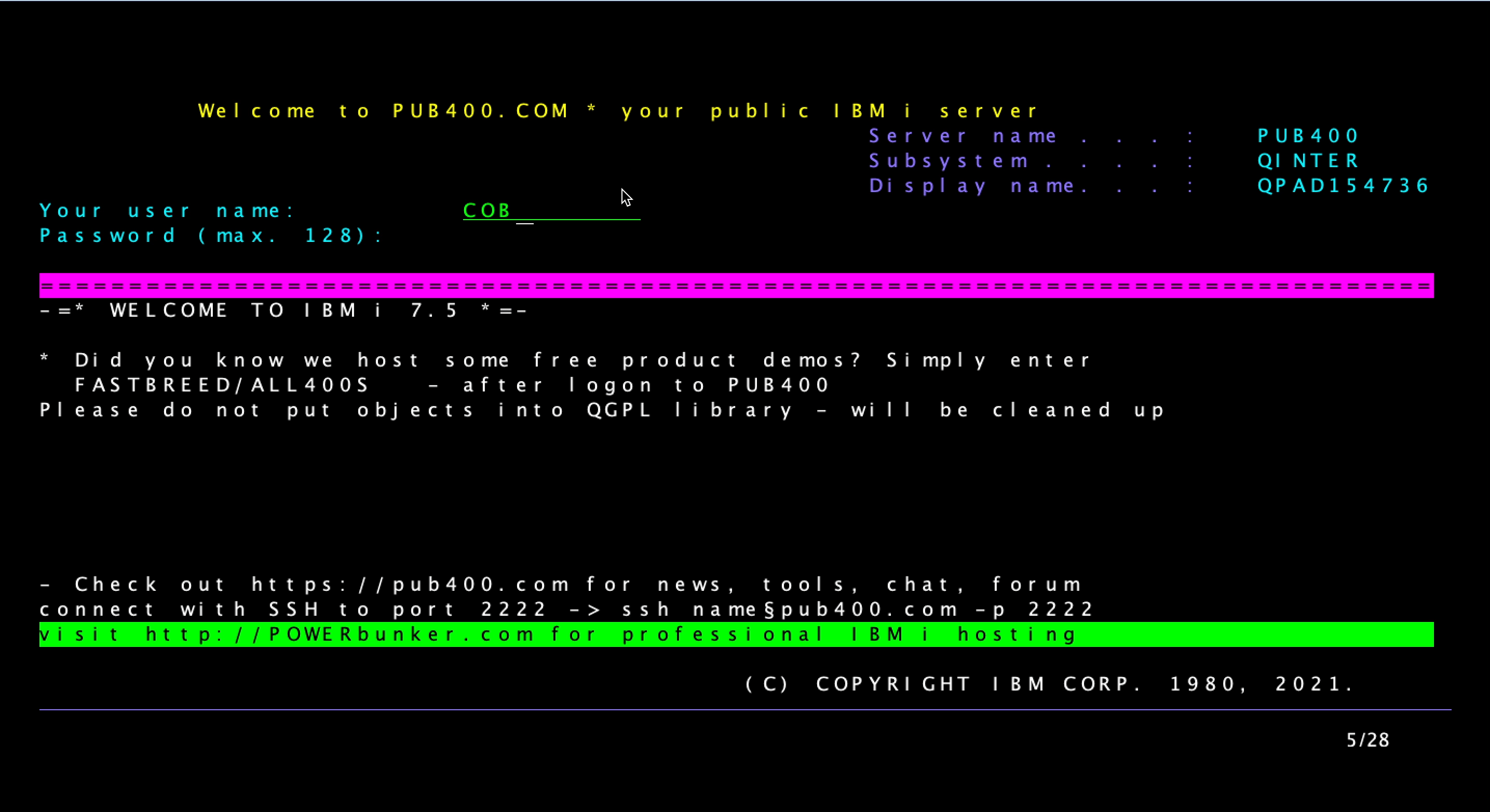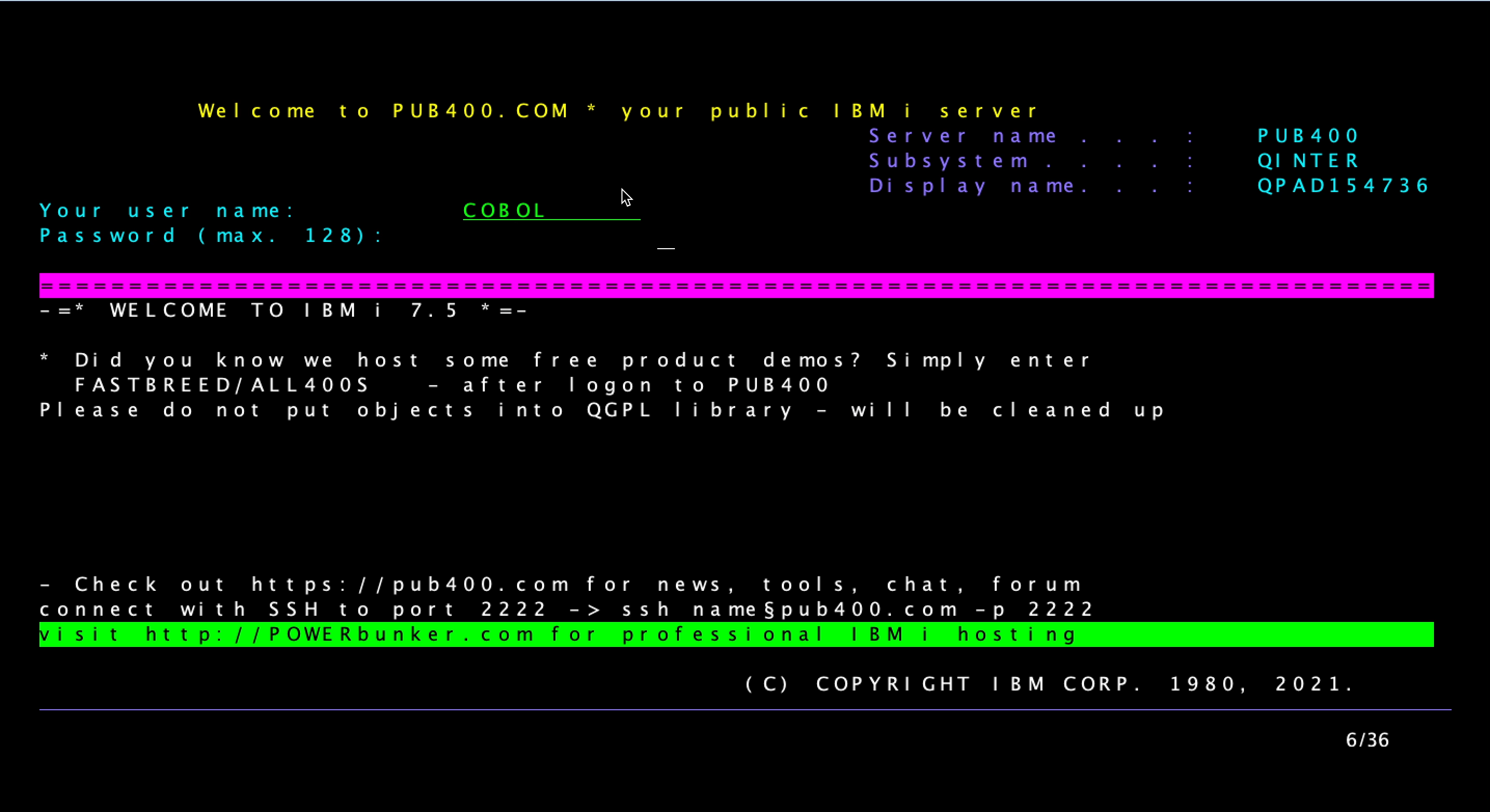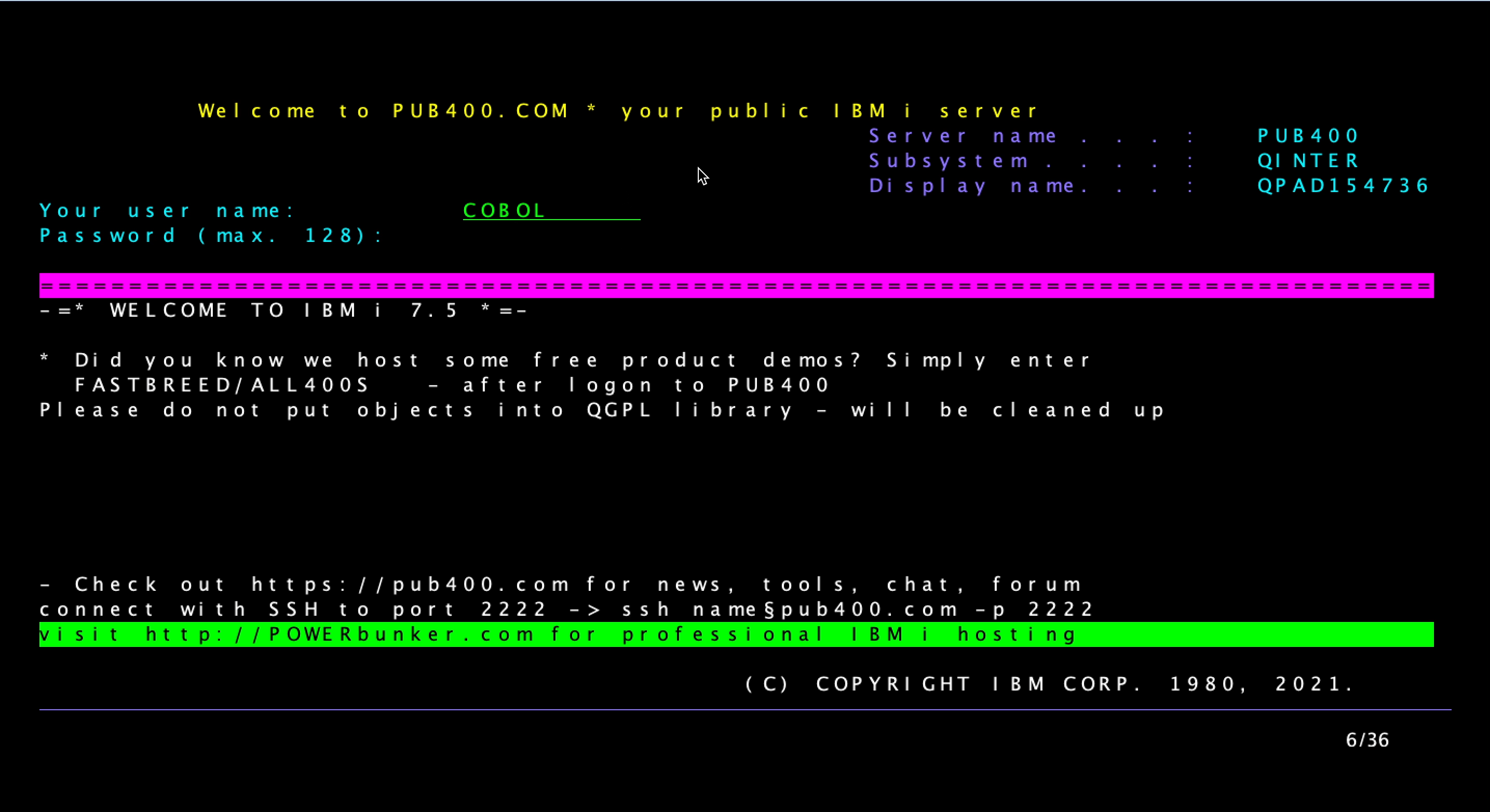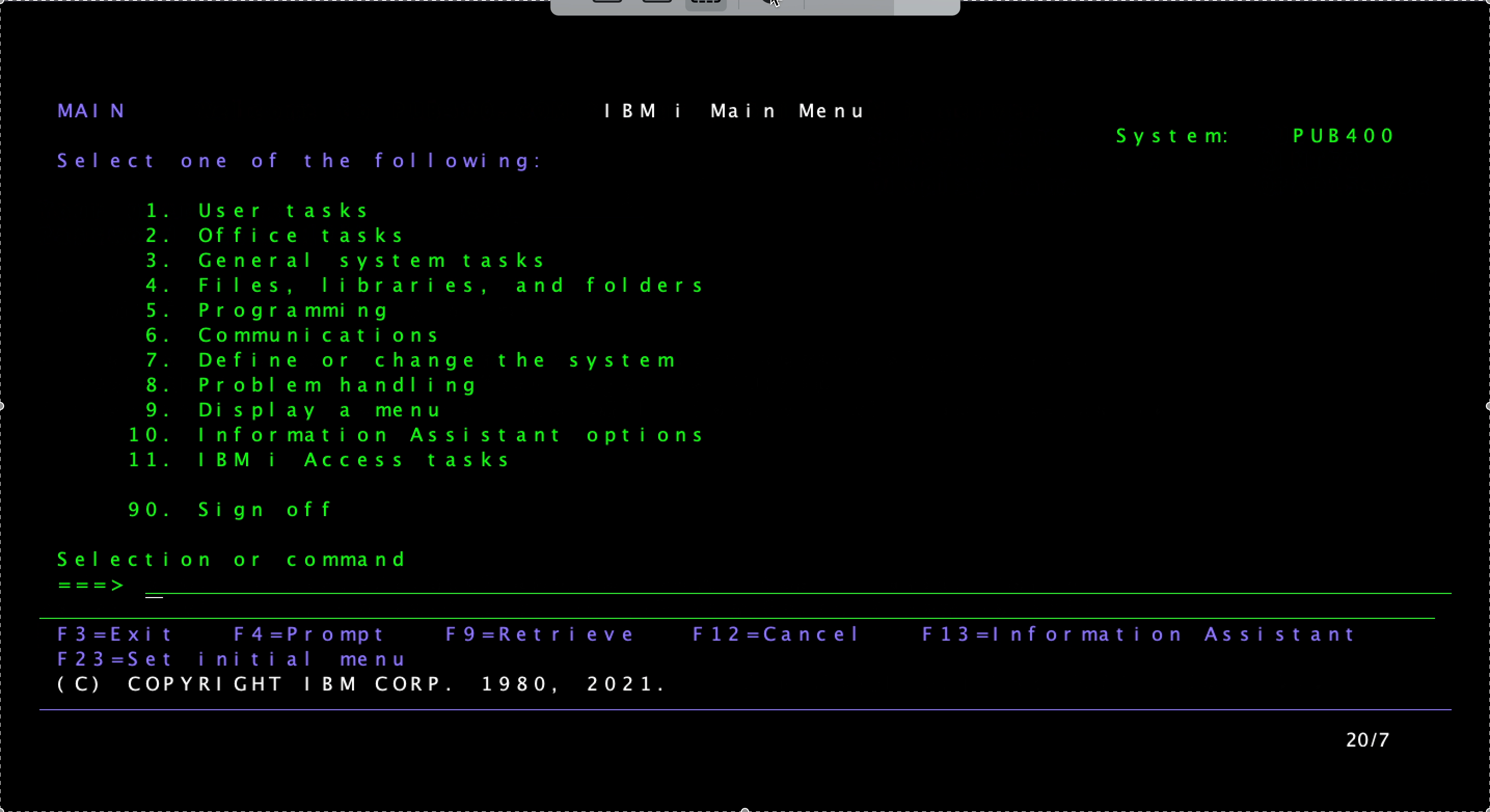
AS400 AS400 简介AS/400操作系统演示 AS400 简介 在 AS400 中,AS代表“应用系统”。它是多用户、多任务和非常安全的系统,因此用于需要同时存储和处理敏感数据的行业。它最适合中级行业,因此用于制药行业、银行、商场、医院管理、制造业、分销…...
FreeRTOS 中断管理介绍和实操
目录 中断定义 中断优先级 相关注意 中断相关函数 1.队列 2.信号量 3.事件标志组 4.任务通知 5.软件定时器 中断管理实操 中断定义 中断是指在程序执行的过程中,突然发生了某种事件,需要立即停止当前正在执行的程序,并转而处理这个…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
